基于k度平滑的多无人机协调路径规划方法
邓 敏,陈 志
(桂林航天工业学院 机械工程学院,广西 桂林 541004)
0 引 言
当前,无人机(UAV)以其灵活机动、成本低、效费比好、可靠性高、操作简便等特点,被广泛应用于各个领域[1,2]。由于无人机的工作环境较为危险,保证无人机飞行轨迹远离各种威胁和限制区域是无人机研发的重要研究领域[3,4]。
针对无人机航迹规划问题,众多专家学者开展了大量研究。文献[5]提出了一种改进的双向A型搜索算法,通过引入无人机搜索角度作为算法搜索的约束,提高了算法的执行效率。文献[6]提出了一种基于参考路径长度与威胁距离的任务点规划方法,通过采用改进差分进化算法获取路径更短且适应度值更优的路径规划方案。但上述无人机路径规划策略均基于单个无人机的解决方案,无法通过协作方式完成较为复杂的多无人机作业任务。因此,针对多无人机的协同路径规划,文献[7]提出了一种基于凸多边形和凹多边形的区域路径规划方法,通过对各个无人机子区域的搜索路径规划,建立区域划分和路径规划的整体调用模型,能够实现多障碍物的有效规避。文献[8]针对多机干扰造成的领航状态失真,提出了一种基于交互式多模型(IMM)算法和自适应差分进化(JADE)算法的路径规划策略,利用运动模型匹配多机运动状态,从而实现多机协同航路优化。但目前针对多机协同路径规划策略大多是在静态威胁情况下进行研究,而对于诸如雷达、无人机反制装置等多动态威胁研究较少[9,10]。
鉴于此,本文在雷达威胁、地形威胁、无人机反制装置威胁等情况下,针对多无人机协同的轨迹规划问题,以k度平滑法为基础提出了多无人机协同路径规划方法。首先,使用Voronoi图法对每个边缘成本进行重新定义和计算,通过改进的蚁群优化算法获得无人机的初始路径,并引入k度平滑方法进行规划路径优化。最后,设计多无人机的强、弱协调方法,并通过仿真和实验验证所提策略的正确性和有效性。
1 运行环境建模
图1为基于Voronoi图的多个威胁因素环境模型[11,12],其中R表示雷达,T表示接地,M表示无人机反制装置。由图1可知,在复杂环境中需要考虑长度、地形、雷达以及无人机反制装置的威胁。可通过对不同类型的威胁源采用不同的处理方法,以确定Voronoi边缘的成本。

图1 基于Voronoi图的多个威胁因素
为了清楚说明多个无人机协同路径规划建模,对运行环境做如下假设:
(1)所有无人机都位于不同的高度,无需进行避碰处理,并简化路径规划在二维空间的操作。
(2)无人机以恒定速度飞行,机群间的通信稳定可靠。
(3)在Voronoi图中将威胁源视为粒子并生成顶点,沿边缘(i,j)的威胁表示为式(1)所示[13,14]
(1)
式中:a、b、c、d为常数,且和为1;Nr、Nt、Nm分别为雷达、地形障碍物和无人机反制装置的数量;Jij,r(n)、Jij,t(n)和Jij,m(n)分别表示为雷达、地形障碍物和无人机反制装置对边缘(i,j)的第n个威胁;Jij,l表示边(i,j)的燃料成本。
其中,雷达威胁的数学表达如式(2)所示
(2)
式中:V为无人机的速度,lij为边缘(i,j)的长度,Rn(t)为无人机与第n个雷达在t时间的距离。
第n个雷达的检测能力Qn的数学表达如式(3)所示
(3)
式中:G表示天线的增益;σ表示雷达的截面面积;Pt表示发射机的功率;R表示雷达到物体的距离;Ae表示天线的有效面积。
Jij,t(n)表示地形威胁,当无人机低空方式飞行时,可将地面山脉作为地形威胁,当无人机接近地面威胁时,此时地面对无人机的威胁也就越大,如式(4)所示
Jij,t(n)=Lne-kdij(n)
(4)
式中:Ln是第n个地形因子的威胁级别,Jij,m(n)为无人机反制装置威胁,表示无人机反制装置的威胁成本由命中率和攻击力决定。假设A是无人机的穿透概率,B是无人机反制装置的攻击能力,pij(n)是第n枚无人机反制装置的检测概率,无人机反制装置对其边缘(i,j)的威胁代价如式(5)所示
Jij,m(n)=B(1-A)pij(n)
(5)
Jij,l为燃料成本,燃料成本与边的长度成正比,其数学表达如式(6)所示
Jij,l=λlij
(6)
将式(4)~式(6)的表达式代入式(1),边(i,j)的总威胁可以表示为式(7)所示

(7)
2 基于改进蚁群算法的路径规划
本文所提出的单个无人机的航迹规划由初始路径规划、平滑机制和协调策略3层组成。
2.1 初始路径规划
蚁群优化算法(ACO)具有信息正反馈、高度并行性和优化能力强的优点[15]。为提高ACO的效率,引入Voronoi边缘成本以及信息素更新,使得在Voronoi环境下更加可行和高效,从而通过威胁成本来确定最佳的飞行路径,同时对全局最佳路径信息进行迭代更新。因此,本节主要采用改进的蚁群优化算法(IACO)解决多无人机的初始路径规划问题。
在IACO中,蚂蚁根据转移概率选择下一个节点,如式(8)所示[16]
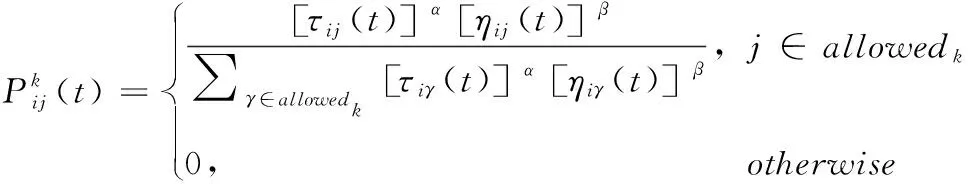
(8)
式中:allowedk为蚂蚁k在节点i上的可用节点;η表示启发式信息;τ表示信息素;α和β分别表示信息素和启发式信息对转移概率的影响参数。如式(9)所示为启发式信息
(9)
式中:Jij表示边(i,j)的成本,且dje表示从节点j到目标点e的欧几里得距离。在迭代中,一旦所有蚂蚁完成了搜索,每个边的信息素就会更新,其数学表达如式(10)所示[17]
τij(t+n)=(1-ρ)τij(t)+Δτij(t,t+n)
(10)
式中:ρ为信息素蒸发速率,Δτij(t,>t+n)为边(i,j)上的信息素增量。其中信息素增量如式(11)所示
(11)
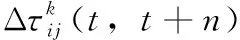

(12)
式中:Lk表示蚂蚁k的路径长度;Q为常数。在蚁群算法中通常利用信息素更新方法来提高收敛速度。
为了有效降低IACO陷入局部最优,同时增强算法的全局搜索能力,在一次迭代最短路径的信息素更新阶段对信息素进行限制,如式(13)所示

(13)
式中:τmin和τmax为边缘上最小和最大信息素。
2.2 平滑机制
图2为单个无人机的路径规划的流程。
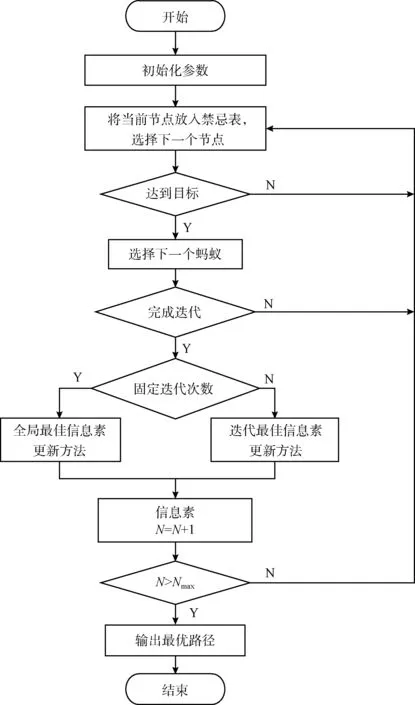
图2 IACO单个无人机的路径规划的流程
由图2可知,在求解多无人机初始轨迹规划中的主要步骤如下:
(1)构建Voronoi环境并计算边缘成本。
(2)确定初始化算法的参数,包括α,β,Q,τmin,τmax,以及蚂蚁数m,初始迭代数N和最大迭代数Nmax。
(3)初始阶段,蚂蚁处于初始节点上,此时将当前节点纳入到禁忌表中,同时根据式(8)选择下一节点,直到达到目标。
(4)选择其它蚂蚁,同时返回上一步骤,直到实现一次完整的迭代过程。
(5)当迭代次数达到要求时,对全局信息素进行更新,否则更新最佳迭代信息素。
(6)根据限制信息素,更新边缘信息素,并返回到(3),直到满足终止条件N>Nmax,并输出最佳路径。
3 k度路径平滑规划
3.1 k度平滑方法
图3为平滑度为k的动态可行轨迹。由图3可知,其中存在一些无法满足无人机转弯约束的小角度。因此,须对Voronoi图中的两条相互连接的路径进行平滑处理。本文以k度平滑方法为基础从而实现初始路径的平滑处理。
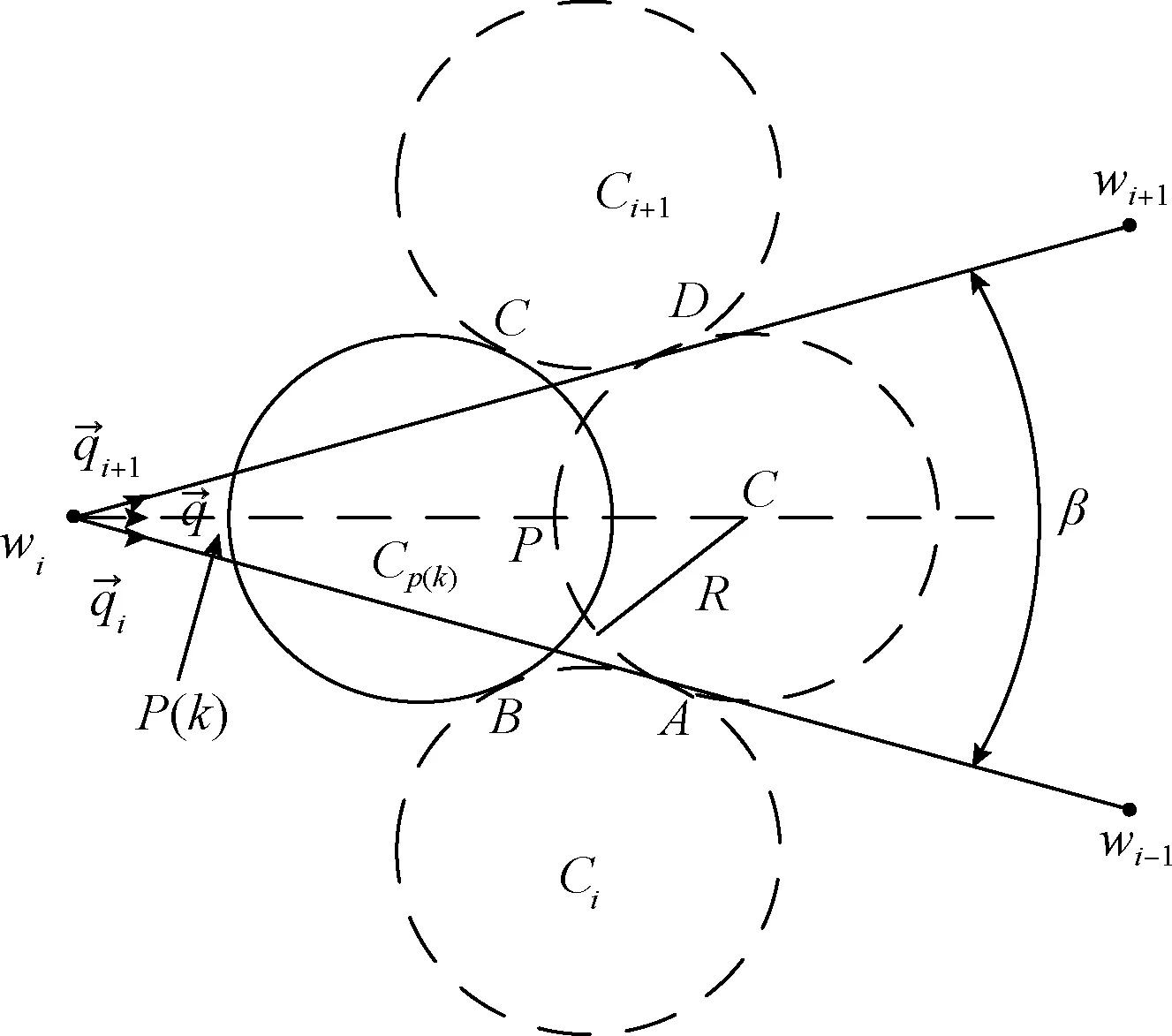
图3 平滑度为k的动态可行轨迹
由图3所示的3个航路点wi-1,wi和wi+1定义航路点路径,其数学表达如式(14)、式(15)所示
(14)
(15)

(16)
令C表示具有最小转弯半径R的内切圆,圆心位于3个航路点形成的角度等分线上,则圆与两条直线在一个点相交,且β的等分线在两个位置与圆C相交。
假设内切圆C沿着β的等分线向wi移动,从而产生圆Cp(k)和wi的交点p(k),平滑度k的数学表达如式(17)所示
(17)
由此可知,图3中k度轨迹是唯一且动态可行的轨迹,它从航路段wiwi-1经过p(k)过渡到航路段wiwi+1。
3.2 理论结果
图4为角度为β的k度平滑。
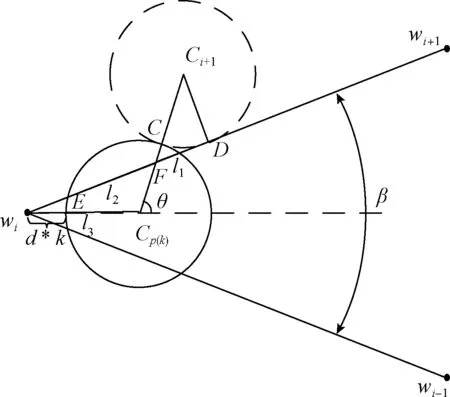
图4 角度为β的k度平滑
(18)
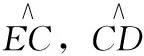

(19)
FD线长度如式(20)所示
l1=Rtanα
(20)
线段wiF的长度如式(21)所示
(21)
由于对称性,可以得到差值Δl的数学表达式如式(22)所示
(22)
p点与wi之间的距离如式(23)所示
(23)
wi与Cp(k)中心的距离如式(24)所示
(24)
可以将k和Δl的关系表示为如式(25)所示
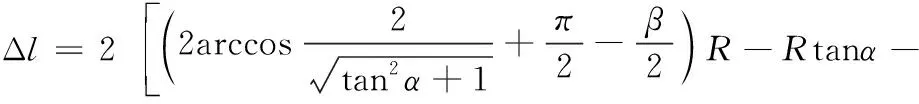
(25)
由式(25)分析可知,当圆Cp(k)沿β的等分线移动时,Cp(k)的中心与wi之间的距离越短,平滑后的路径总长度就越长,其关系如图5所示。由图可知,若k=0,则Δl>0;若k=1,则Δl<0。由于函数单调递减,因此只有一个值可以使Δl= 0。由此可知,通过更改k的平滑度值,可以获得与点路径wi-1wiwi+1相同的路径长度。
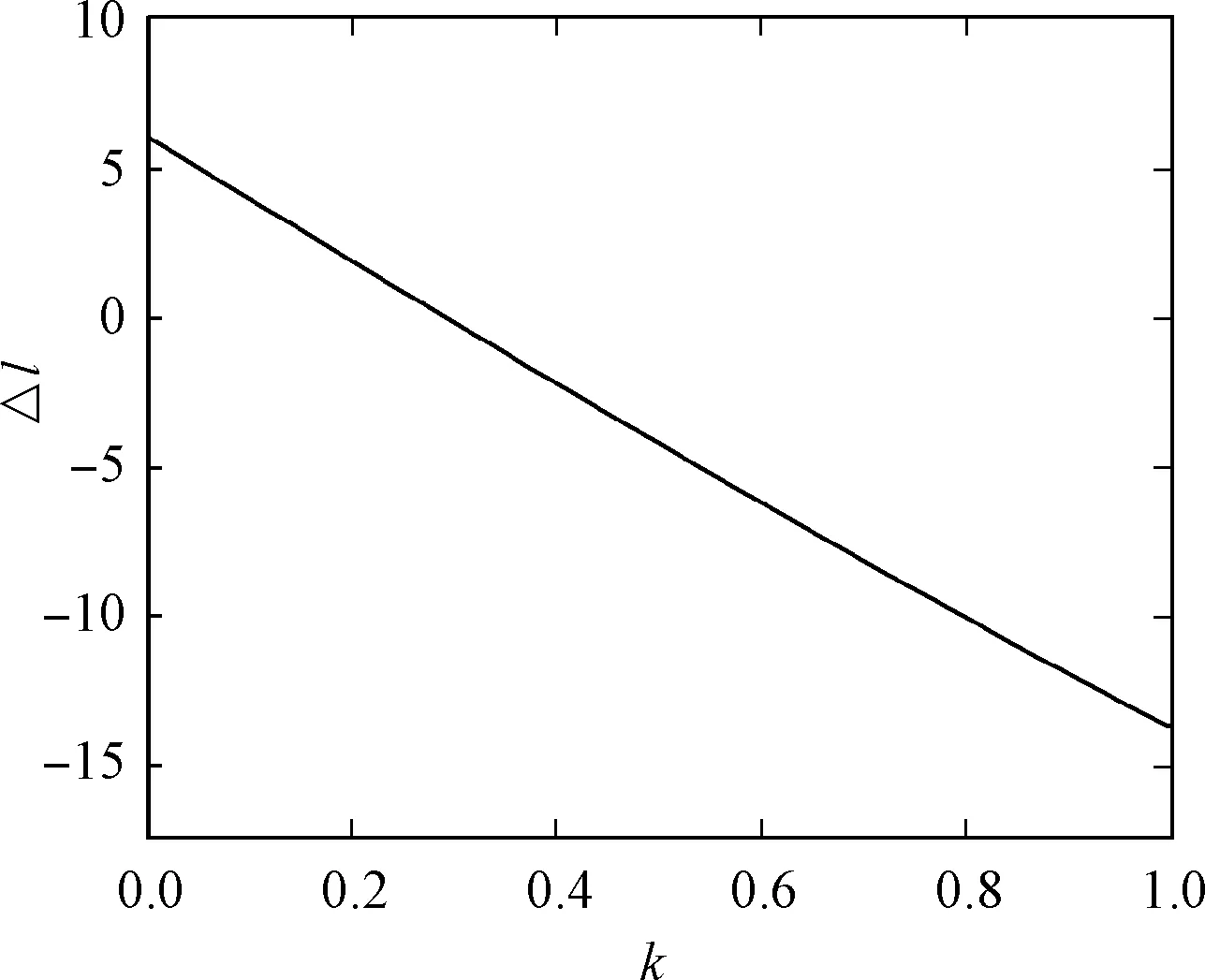
图5 在β=π/3,R=10的条件下,Δl和k的关系
3.3 多无人机协调策略
通过上述分析可以发现,当采用k度方法来平滑无人机路径时能够更形象地表示出实际的飞行轨迹。但是相对多无人机路径规划而言,尚存在多无人机路径协调规划问题。鉴于此,本文提出了一种多无人机协调路径规划方法。
根据协调标准,多架无人机需要在相同时间从初始位置出发,并以最小成本到达目的地,多无人机之间需要协调规划,其协调标准如下:
(1)强协调:要求多个无人机同时达到目标。
(2)弱协调:表示多个无人机在可接受的时间间隔内达到目标。
多个无人机之间的协调为:假定单次任务中有n架无人机参与飞行,且每架无人机以固定的速度V进行飞行。其中,第i架无人机的预期轨迹长度为Li,通过k度平滑方法处理后,此时轨迹长度的上、下限分别为Li,max和Li,min,第i个无人机的路径长度如式(26)所示
Li∈[Li,min,Li,max]
(26)
对于有n架无人机的无人机编队,假设
A=max{L1,min,L2,min,…,Ln,min}
(27)
同时
B=min{L1,max,L2,max,…,Ln,max}
(28)
图6为无人机的可行路径长度间隔。
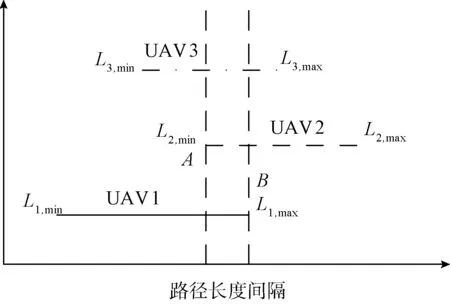
图6 无人机的可行路径长度间隔
由图6可知,如果A-B≤0,则多无人机系统可以实现强协调,表示每个无人机的轨迹间隔都具有非空交叉点I,其数学表达如式(29)所示
I=[L1,min,L1,max]∩[L2,min,L2,max]∩…∩[Ln,min,Ln,max]
(29)
对于非空隙路口I,假设Lm∈I,且不同无人机的平滑路径必须满足路径长度Lm。当处于强协调情况时,Lm表示标准轨迹长度。对于A-B=0这种情况,因为交点I中仅存在唯一元素,为了能够达到强协调效果,不同无人机之间应当使用唯一的选择作为标准轨迹长度。
一旦获得标准长度,采用Greedy算法计算每个角度的k值,确定终端轨迹,对于第i个无人机的轨迹长度角如式(30)所示
Ani={βi1,βi2,…,βip}
(30)
根据平滑原理,对于第i个无人机的初始路径的第j(j∈[1,p])个角,路径长度有相应的最大增量和最小减量。相应地,在弱协调中,多个无人机在可容忍的时间间隔内到达目的地,假设时间间隔是无人机容忍时间间隔的最小值,其数学表达如式(31)所示
Δt=min{Δt1,Δt2,…Δtn}
(31)
如果A-B>0,则交点I为空,且无人机编队无法完成强协调;如果AB≤ΔL,则可以实现弱配位。将标准路径长度标记为Lim(Lim∈[B,>A]),如式(32)所示
(32)
由此可知,当A-B>ΔL时,无法实现强协调或弱协调。图7为多无人机协同路径规划的流程。

图7 多无人机协调路径规划流程
从图7可以看出,当多无人机确定了最终的协调策略以及路径长度,此时可以分别计算不同无人机之间的路径长度差,另外可以根据路径长度差机上角度k值,最后获得不同无人机的平滑协调路径。
4 实验仿真和分析
为验证基于k度平滑方法的多无人机协同路径规划的可行性和有效性,对所提策略进行了仿真分析。仿真实验在CPU主频2.11 GHz、内存1.75 GB的PC机上采用Matlab7.0进行。实验中采用的雷达工作频率为94 GHz,发射功率为20 dBm,带宽为1 GHz,距离分辨率为15 cm,截面面积为3.2 m2;无人机反制装置利用高增益四波段天线单元在有限的空间设计4个波段的高增益天线,其每个波段天线不能受其它天线的影响而异化,天线波束小于40度,天线增益大于15 dB。其中,无人机实验区域范围为100 km×100 km,在该范围内设置有4个静态接地威胁、4个反制装置威胁和8个雷达威胁。
4.1 改进蚁群算法与蚁群算法的收敛速度比较
参考初始化参数,令蚁群大小为50;最大迭代次数为150;信息素权重α和启发式信息权重β分别为1和5;信息素蒸发率ρ为0.1;信息素范围为[0,500]。
随后,将蚂蚁放在原始节点上,同时将对应的节点放入到禁忌表中,然后利用式(8)选择下一个节点,直到找到最终目标为止。最后,根据式(13)的限制信息素,更新边缘的信息素并重复该过程,直到使用相同的参数分别对两种算法执行150次迭代,其结果如图8所示。

图8 加权路径长度和迭代中ACO和IACO的比较
由图8可知,在相同情况下IACO需进行37次迭代可收敛,而ACO需进行70次迭代,且当两条线在第70次迭代时重合,并在此之后保持稳定。表示该最短路径不会改变,且后者相比前者收敛速度提高了47%,解决了局部最优和收敛速度低的问题。
表1为二者的比较结果,其中包含平均加权路径长度、收敛迭代以及最短加权路径长度的比较。由表1可知,IACO不仅能够实现更高的收敛速度,还拥有与ACO相同的最短加权路径长度和更低的平均加权路径长度。通过IACO搜索算法,平均加权路径接近最短加权路径,表明IACO具有良好的有效性和效率。

表1 ACO和IACO的比较
4.2 平滑初始轨迹
假设从初始位置到目的地只有一架无人机,且需要平滑初始轨迹的角度才能满足该无人机的转弯限制。在该仿真中,假定初始路径由IACO生成的,所提的k度平滑方法和协调策略可用于获得最佳飞行路径,其仿真结果如图9所示。
由图9可知,初始路径的长度为158.20。当k=1时,无人机沿旋转角的内接圆飞行,此时平滑路径长度最小,为125.90。同时,当k=0时,内切圆移动到航路点,此时平滑路径长度最大,为164.74。由此可知,平滑路径长度在区间[125.90,164.74]之间,且在特殊情况下,平滑的路径具有与初始路径相同的路径长度。由此可知,在实际情况下,最终的可飞行路径长度分布在从最小到最大的间隔内。

图9 单个UAV的平滑路径
4.3 多无人机协调仿真
本次仿真过程中,将随机生成16个节点,并将生成的节点作为环境威胁,从而进行弱协调和强协调仿真。
4.3.1 强协调仿真
图10为强协调性仿真轨迹。
由图10(a)可知,通过所提策略可成功规划不同无人机从不同起点同时到达同一目标的路径,其详细信息见表2。同时,在另一高度协调的情况下,分配两架无人机以不同的起点达到目的地目标,其仿真轨迹如图10(b)所示,表3为该轨迹的详细信息。从表3可知,计算可得最终路径长度为97.98,表明该策略具有良好的强协调性。此外,对3个无人机组成的编队进行分配,以同时到达同一目的地为目标,图10(c)为优化轨迹路线图,轨迹的详细信息见表4。由此可知,本文所提出的强协调策略能够有效实现多无人机的协同轨迹规划问题,同时能够实现多无人机同时到达目标位置。

表2 到达同一目标的两架无人机的高度协调信息

表3 两架到达不同目标的无人机进行强力协调信息

图10 到达相同目标的3架无人机

表4 到达同一目标的3架无人机进行强力协调信息
4.3.2 弱协调仿真
在实际运行中,多无人机无法准确实现强协调,但对于非紧急任务,可使无人机在一定时间间隔内到达目标位置,即为弱协调仿真。实验中以两架无人机为对象,且两架无人机分别位于不同的起始点,要求在规定时间内两架无人机能够到达同一目标位置,计算轨迹间隔得到UAV1的轨迹间隔为[89.47,90.74],UAV2的轨迹间隔为[91.23,91.43]。该两间隔的交集为空,表示UAV1和UAV2无法实现强协调。假设路径长度的容许变化ΔL(ΔL=VΔt)为2 km,根据协调策略,可实现弱协调,如图11(a)所示,轨迹的详细信息见表5。
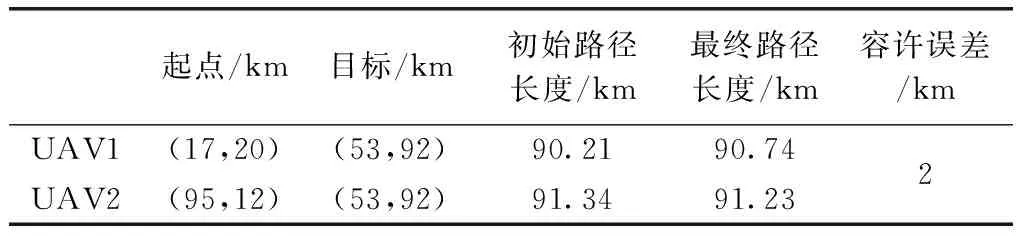
表5 两架到达同一目标的无人机弱协调信息
分析可知,两架无人机的最终路径长度分别为90.74和91.23。在其它弱协调的情况下,由3架位于不同地点的无人机组成编队,在可接受的时间间隔内到达同一目的地。通过计算,这3架无人机的轨迹间隔分别为[60.19、60.80],[61.19、61.22]和[60.68、60.95],图11(b)为3架无人机的优化轨迹,表6为其轨迹的详细信息,计算可得该3架无人机的最终路径长度分别为60.19、61.20和60.95。由此可知,本文所提弱协调策略能够有效补充强协调能力,有助于解决多无人机只能在可接受的时间间隔内到达目标的问题。
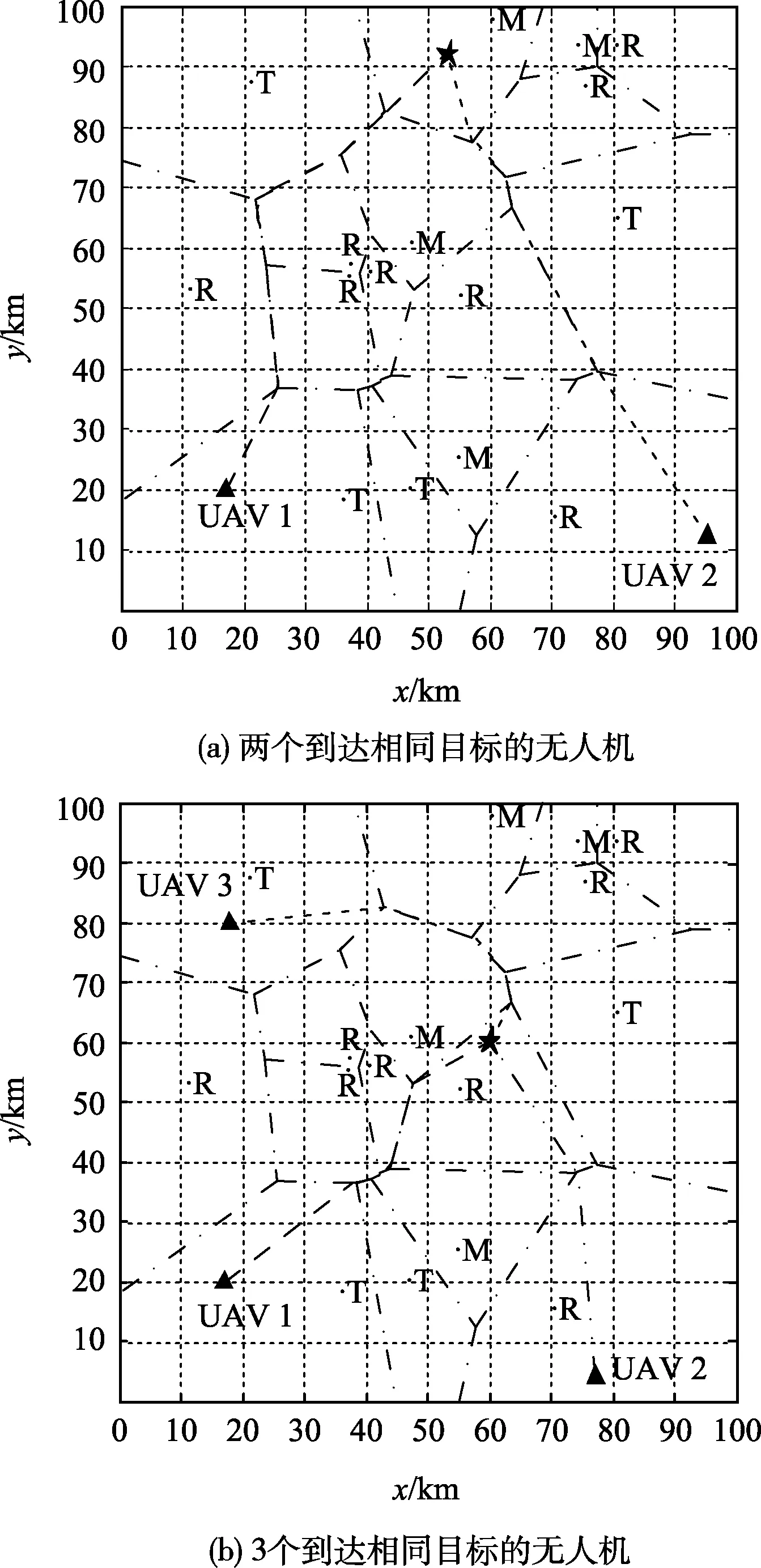
图11 弱协调性轨迹
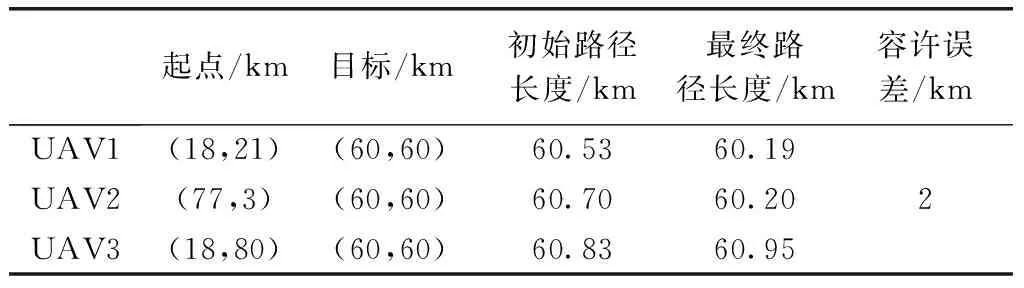
表6 到达同一目标的3架无人机弱协调信息
5 结束语
针对多无人机协同的轨迹规划问题,提出了一种基于k度平滑法的多无人机协同路径规划方法。通过仿真实验与对比分析得出以下结论:①本文所提强协调策略可有效解决多无人机协同的轨迹规划问题,并允许多无人机同时到达目标位置、同时完成任务;②本文所提弱协调策略可补充强协调能力,有助于解决多无人机无法同时到达目标的问题。然而,本文模型在环境构建方面较为单一,因此后续将重点研究多无人机协同路径在复杂动态环境和不确定情况下的路径规划。

