基于迁移子空间的半监督领域自适应方法
陶 洋,杨 雯,翁 善,林飞鹏
(重庆邮电大学 通信与信息工程学院,重庆 400065)
0 引 言
在实际应用中,传统机器学习算法面临着缺乏标签样本的困境。近年来,迁移学习和领域自适应方法得到广泛研究,这类方法将源域(训练集)丰富的知识迁移到目标域(测试集)来解决缺乏标签问题[1-3]。基于特征表达的领域适配方法通过原始空间或投影空间中的特征表示实现源域和目标域之间的对齐[4-6]。Zhang等[7]提出了隐稀疏域迁移模型,在域之间联合学习稀疏编码和最优子空间,挖掘子空间中源域和目标域共有的隐藏结构。B.Sun等[8]提出子空间分布对齐法,在子空间对齐的基础上增加了概率分布自适应,对源域和目标域进行二阶特征变换,实现源域和目标域数据对齐。然而这些方法都没有很好地利用样本的标签信息提高分类性能,因此一些方法结合了分类器设计和特征表示算法的优点,利用了样本的标签信息增强了模型的判别性[9-11],还有一些方法利用样本标签,挖掘了重构矩阵所包含的样本之间的类内与类间信息,提高模型的分类性能[12]。本文中,主要研究了基于特征表示的领域自适应,并提出了基于迁移子空间的半监督领域自适应方法(semi-supervised domain adaptation via transfer subspace,SSDTS)。该方法利用类别标签先验信息,进一步分析同类样本之间的相似性和异类样本之间的差异性,得到鉴别性共享子空间和具有块对角结构的类重构矩阵,最终提高模型的分类性能。
1 相关理论
1.1 子空间学习
子空间学习(subspace learning,SL)是基于某一特定准则,将原始高维的样本变换到低维、有意义的子空间中,其目的是为了找出数据的内在结构[13,14],得到能反映原始样本分类本质的低维特征。子空间学习的任务有两个,一是寻找针对模式最具鉴别性的描述,用较低维度的特征描述原始样本并保留分类所需的鉴别信息。二是原始数据进行维度约减后,能减少后续运算的计算量,提高运算速度。
1.2 稀疏表示和低秩表示
子空间学习方法中的两大重要理论包括稀疏表示(sparse representation,SR)和低秩表示(low-rank representation,LRR)。其中稀疏问题来自域信号处理领域的压缩感知(compressive sensing,CS)。稀疏性是指为了更好地对复杂的多维图像进行描述,可以将图像信号看成是由适当选取的一组过完备基中少数几个基的线性组合,即用最少基的线性组合来表达图像信号,得到信号在这组基上的稀疏表示。稀疏表示能从大量样本中发掘数据的内在结构,具有良好的自适应性和鉴别性,然而其在求解过程中缺乏对整体样本结构的全局约束,因此难以有效发掘样本的全局结构。矩阵的稀疏性可以通过秩来度量,具有很强的全局约束。低秩表示系数矩阵可以增强对噪声的抵抗能力。当数据来自多个独立子空间时,低秩表示能够准确发现数据本身蕴含的多子空间结构。此时获得的低秩表示系数矩阵会呈现块对角形式,每个块对应每个子空间。
2 基于迁移子空间的半监督领域自适应方法
2.1 方法概述
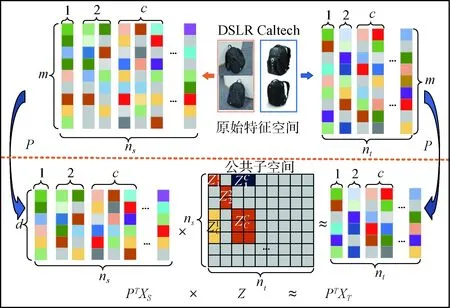
图1 SSDTS算法整体框架
2.2 问题建模
迁移子空间学习的目标是找到一个投影矩阵,通过投影矩阵将源域数据和目标域数据投影到共享子空间,在子空间中源域和目标域样本分布大致相同。本文提出的方法假设在共享子空间中目标域数据可以由源域数据线性重构,可形式化的表示为
(1)
其中,φ(·)是原始特征空间到再生希尔伯特空间的非线性映射,P是投影矩阵,Z是重构矩阵。稀疏表示是局部约束,能够发现数据间的局部线性关系,对重构矩阵Z施加稀疏约束,不仅可以保留数据的局部结构,而且使每个目标域样本可以被少量源域样本更好地重构。低秩性不仅有利于揭示块对角结构,还能够保留数据的全局结构。对重构矩阵Z施加低秩约束使矩阵具有块对角结构,获得源域样本和目标域样本的一致表示,使源域样本和目标域样本在共享子空间中可以很好地对齐。对重构矩阵Z同时施加稀疏和低秩约束后可得
(2)
(3)
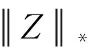
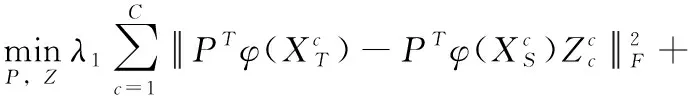
(4)
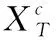

(5)
利用样本的先验类别信息,将严格的二值标签矩阵松弛为变量矩阵,增大投影后不同类样本之间的距离,挖掘样本内蕴含的鉴别信息,加强投影后子空间中样本的判别性,以此提高分类性能。式(5)可以表示为
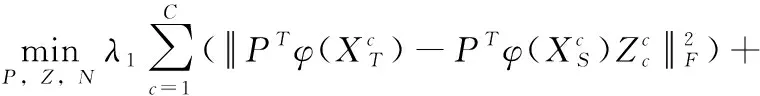
(6)
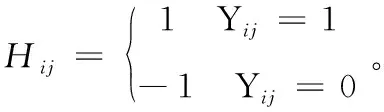

图嵌入方法能够保证相同类的样本在转换后能紧密地聚集在一起,避免过拟合。引入了类紧致图(class compactness graph,CCG)作为正则项。在类紧致图中,同一个类的两个不同样本通过无向边连接,因此类紧致图的权重定义为
(7)
其中,σ表示核参数,可以通过下式(8)使得转换后的同类样本紧密聚集在一起
(8)
其中,fi=xiP表示转换后的第i个训练样本xi,L表示拉普拉斯图,定义为L=D-W,D为对角矩阵,对角元素为Dij=∑jWij。联合式(6)和式(8),最终定义的目标函数如下

(9)
2.3 模型优化求解
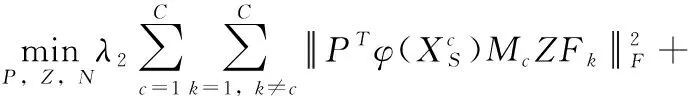
(10)
其中,k(·)是核函数,满足条件k(xi,xj)=〈φ(xi),φ(xj)〉=φ(xi)Tφ(xj)。令K=φ(X)Tφ(X),Ks=φ(X)Tφ(Xs)和Kt=φ(X)Tφ(Xt)表示核格列姆矩阵。通常最优投影矩阵P可以直观地表示为φ(X)的线性组合,即P=φ(X)Φ。将其代入到式(10)中,可以得到
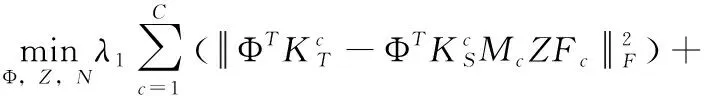
(11)
为了求解式(11),采取了变量交替优化策略,即固定其它变量来迭代更新每个变量。通过对重构矩阵Z引入两个辅助变量J和T,将引入新辅助变量的最小化问题重新写成

(12)
通过增强的拉格朗日乘数(augmented lagrange multiplier,ALM),上述式(12)可以转换为以下最小化问题
(13)
其中,Y1和Y2是拉格朗日乘子,μ>0是惩罚参数。上述式(13)问题可以通过不精确拉格朗日法(inexact augmented lagrange multiplier,IALM)解决,具体步骤如下所示:
步骤1更新Φ,固定变量Z,J,T和N,解决优化式(14)来更新Φ

(14)

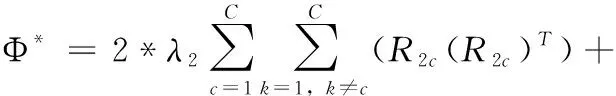
(15)
其中,式(15)中的A=Y+B⊙M。
步骤2更新J,去掉与J无关的项后,式(13)可以重新写成下列形式

(16)
式(16)可以进一步写成下列形式
(17)
通过奇异值阈值(SVT)算子可以有效地解决式(17)。
步骤3更新T,去掉与T无关的项后,式(13)可以重新写成下列形式
(18)
式(18)可以进一步写成下列形式
(19)
利用收缩算子对式(19)求解,结果如下所示
(20)
步骤4更新Z,去掉与Z无关的项后,式(13)可以重新写成式(21)形式
(21)
通过式(21)很难得到Z的封闭解,根据梯度下降算子,可以得到解ZK+1的表达式
(22)
其中,Z的导数可以表示为式(23)
(23)
步骤5更新N,可以通过解决式(24)问题更新N
(24)
令ΦTK-Y=I,考虑N的第(i,j)项Nij,可以得到下式
(25)
Nij的最优解是
Nij=max(IijHij,0)
(26)
因此,N的最优解也可以改写为
N=max(I⊙H,0)
(27)
表1中详细总结了所提算法的迭代优化过程。

表1 SSDTS算法迭代流程
3 实验验证与结果分析
本文使用的基准数据集分别是:Office、Caltech256、COIL、MNIST和USPS数据集。为了验证本论文提出算法的性能,在上述基准数据集上进行实验,并与多个相关的经典领域自适应算法,即SGF、GFK、JDA、LTSL、SA、LSDT、CORAL、LRSR算法进行对比。本文提出的SSDTS算法选择K-最近邻分类器作为分类器。由于SSDTS算法是半监督迁移学习算法,目标域中存在部分标签,故使用源域样本与少量有标签目标域样本训练分类器,然后使用无标签目标域样本测试分类效果。文中所有实验均重复了20次,最后记录平均分类正确率。
3.1 数据集介绍
Office数据集是可视化领域适配的基准数据,该数据集包括了来自亚马逊(Amazon)、数码单反(DSLR)和网络摄像头(Webcam)3个域中的常见对象类别。在Office数据集中,每个域包含31个不同的对象,共有4652张图像。Caltech256数据集包含了256个类别,共有30 607幅图像。Office和Caltech数据集的部分图像样例如图2所示。将Amazon用符号A表示,DSLR用符号D表示,Webcam用符号W表示,Caltech256用符号C表示,利用这4个域中共有的10个类别进行实验。任意选取两个域作为源域和目标域进行实验,一共可以得到12组相关实验。根据文献[12]中的设置,实验中,当Amazon作为源域时,则从每类中随机选择20个样本作为源域数据集,如果是DSLR、Webcam和Caltech256作为源域,则从每类中随机选择8个样本作为源域数据集。当4个域的样本作为目标域时,从每类中随机选择3个样本作为目标域数据集,剩下的作为测试数据集。对于Office和Caltech256数据集采用SURF特征和DeCAF6两种特征进行实验。

图2 Office和Caltech256数据集图像样例
USPS和MNIST数据集都包含10个类,分别是数字0-9,两个数据集的部分样例如图3所示。USPS数据集中,包含训练图像7291张和测试图像2007张,共有9298张图像。MNIST数据集中,包含60 000张训练图像和10 000张测试图像,共有70 000张图像。在实验中,从两个数据集中随机选择10 000张图像分别作为实验中的源域和目标域,一共可以得到2组相关实验。当USPS和MNIST数据集作为源域时,则从每类中随机抽取100个样本作为源域数据集,当USPS和MNIST数据集作为目标域时,从每类中随机抽取10个样本,共100个样本作为目标域数据集,其余未抽取样本作为测试数据集。

图3 USPS和MNIST数据集样例
COIL-20数据集包含了20类对象,共1440张图片。该数据集中的部分样例如图4所示。

图4 COIL数据集样例
在本次实验中,数据集被划分为两个子集C1和C2,两个子集各有720张图像。将C1和C2交替作为源域和目标域可以得到2组实验。当C1和C2子集作为源域时,选取子集中的所有样本作为源域数据集,当C1和C2子集作为目标域时,从所有类别的样本中随机抽取270个样本作为目标域数据集,剩余未抽取样本作为测试数据集。
3.2 实验结果对比
在Office+Caltech256(SURF)数据集上进行分类实验的结果具体见表2,在Office-Caltech256(DeCAF6)数据集上进行分类实验的结果见表3,在USPS和MNIST数据集上进行分类实验的结果见表4,在COIL数据集上进行分类实验的结果见表5。下面4个表中部分实验结果引自文献[12]和文献[15],粗体数字为每个任务的最优分类结果。
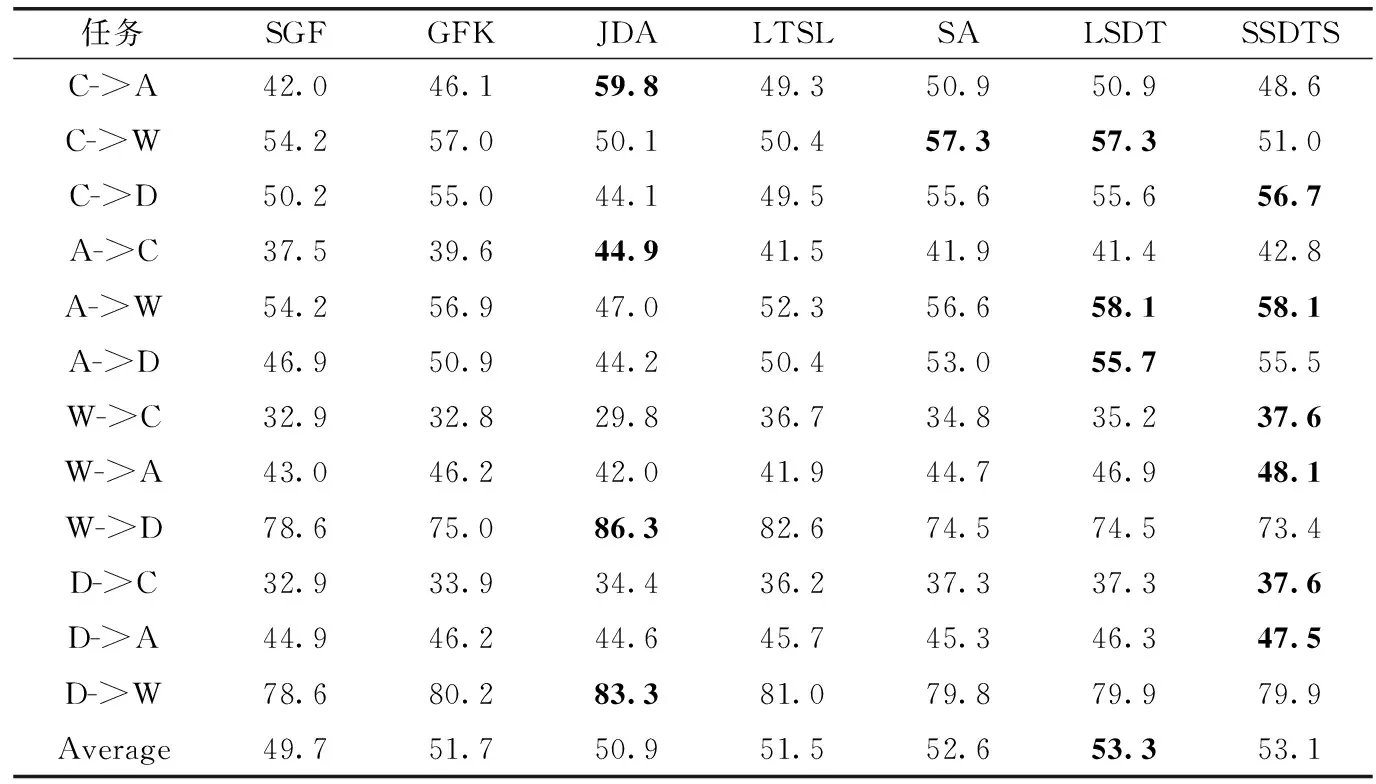
表2 在Office+Caltech256数据集(SURF)上的分类结果
综合以上各组实验结果可以看出,SSDTS算法在上述4个数据集共28个任务中,有21个任务的分类正确率超过了其它对比算法。除了Office-Caltech256数据集(SURF),SSDTS算法在其余的数据集中各任务的平均分类正确率均超过了其它算法,验证了在对齐领域总体分布时考虑样本的先验类别信息有利于提高分类正确率。
如表4所示,在USPS和MNIST数据集上,任务“M->U”的分类准确率都不同程度高于任务“U->M”,这是因为MNIST数据集规模大于USPS数据集,提供的分类信息更加充足。如表5所示,在COIL数据集中的两个任务都取得了最优分类结果,平均分类准确率达到了94.3%,比最优对比方法LRSR提高了2.6%。如表3和表4所示,在(DeCAF6)Office-Caltech256数据集、USPS和MNIST数据集上的任务中,SSDTS算法的分类准确率均高于LRSR算法,这表明利用样本类标签,逐类考虑同类样本的相似性和异类样本的差异性,挖掘重构矩阵中所蕴含的判别信息的有效性。

表3 在Office+Caltech256数据集(DeCAF6)上的分类结果
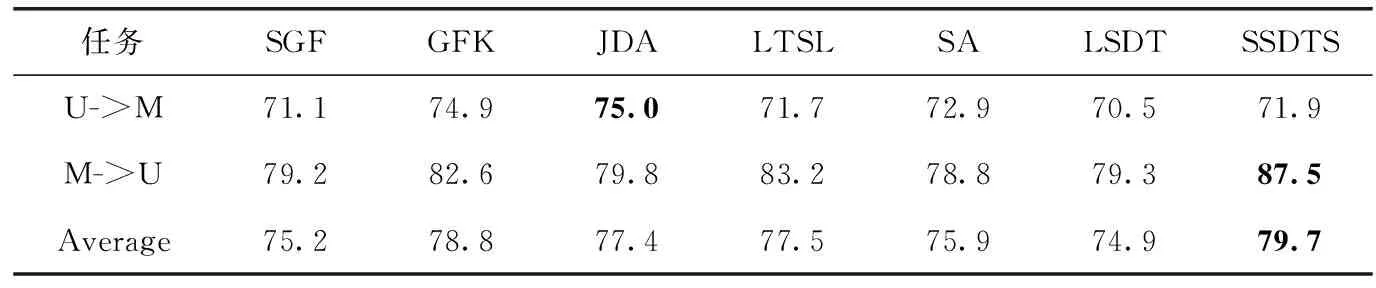
表4 在USPS和MNIST数据集上的分类结果

表5 在COIL数据集上的分类结果
3.3 重构矩阵可视化
引入样本的类标签信息,获得具有块对角结构的类重构矩阵,可以进一步挖掘样本中蕴含的鉴别信息,揭示同类样本之间的相似性和不同类样本之间的差异性,有助于提高分类性能。如图5所示,在Office-Caltech256(DeCAF6)数据集的实验中,对重构矩阵Z进行可视化,可以看到重构矩阵Z呈现出块对角结构,也就是说目标数据中的第c类样本可以很好地由同类的源域数据线性表示。
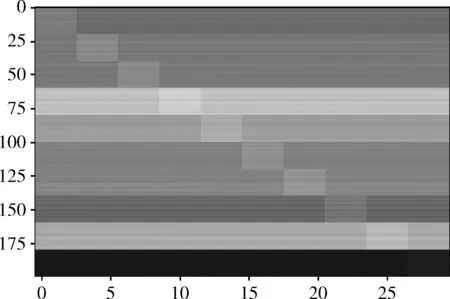
图5 重构矩阵可视化
3.4 参数敏感性分析
如式(10)所示,SSDTS算法模型有λ1和λ2两个参数。为了验证参数的有效性,本节实验测试了λ1和λ2两个参数不同值的组合下对SSDTS算法性能的影响。在Office-Caltech256(DeCAF6)数据集的A->D任务和USPS-MNIST数据集的M->U任务上进行实验。参数λ1和λ2的取值范围设置为{10-3,10-2,10-1,1,101,102}。不同参数组合对分类正确率的影响如图6所示。可以看出,不同的分类任务中对于参数λ1、λ2取值的敏感度不同。在A->D任务中,当参数λ1=0.01,λ2=0.1时,得到最大分类准确率,在M->U任务中,当参数λ1=100,λ2=10时,得到最大分类准确率。表明在不同跨域任务中,相同类之间的类内依赖和不同类之间的类间独立并不是同等重要。
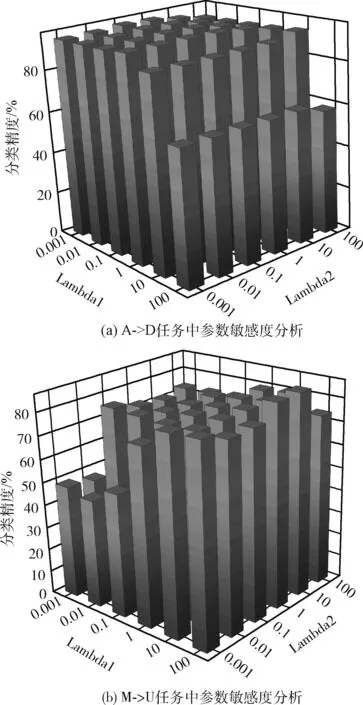
图6 重构矩阵可视化
3.5 算法运行时间对比
本节对比了SSDTS算法与GFK、JDA、LSDT和LTSL算法的运行时间。所有的测试都在一台CPU为Intel 1.8 Ghz双核处理器、内存为8 GB的计算机上完成,软件平台选定为MATLAB R2018b。本节实验在Office-Caltech256(DeCAF6)数据集的W->D任务和COIL数据集的C1->C2任务上进行实验,各个算法的执行时间见表6。其中LSDT算法的运行时间最短,其次是SSDTS算法。LTSL算法的运行时间最长,这是因为该算法的收敛速度相较于其它算法较慢。
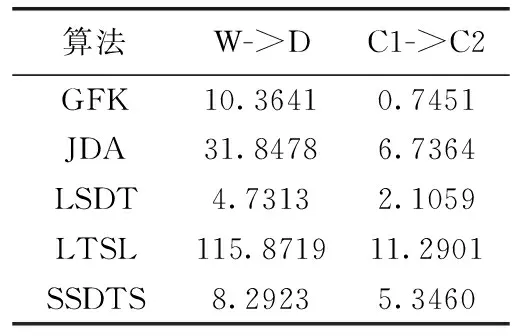
表6 算法运算时间对比/s
4 结束语
针对领域自适应在跨领域图像识别中存在领域偏差、数据特征分布不一致的问题,本文提出了一种基于迁移子空间的半监督领域自适应方法(SSDTS),通过投影矩阵将源域样本和目标域样本投影到低维共享子空间中,使得目标域样本被同类别源域样本线性重构,从而减少源域和目标域之间的差异。此外,为充分发掘同类样本之间的相似性和异类样本之间的差异性,利用样本的标签信息,得到具有块对角结构的类重构矩阵。不同于现有的迁移子空间算法,SSDTS模型能够充分发掘和利用领域间共享标签先验知识,同时考虑子空间的判别性以及重构矩阵蕴含的判别信息。在4个领域自适应公开数据集(COIL、USPS-MNIST、Office-Caltech-SURF、Office-Caltech-DeCAF6)上进行实验,结果表明SSDTS算法优于现有大多数方法。

