多测度融合的树形滤波立体匹配算法
杨 科,刘 凯
(四川大学 电气工程学院,四川 成都 610065)
0 引 言
立体匹配的过程可以概括为匹配代价计算、代价聚合、初始视差计算和视差求精4个步骤,并根据代价聚合方式将匹配算法划分为全局算法和局部算法两大类[1]。全局算法[2,3]主要采用全局优化理论方法估计视差,建立并最小化全局能量函数得到最优视差值,计算精度较高,但是运算效率低,实时性差。局部算法[4,5]给定图像中一点并在其邻域内的一个窗口中,根据某种相似性度量,寻找与子窗口图像最相似的子图,其运行效率高且易于实现,但容易陷入局部最优解。近年来,随着深度学习的不断发展,一些深度学习方法[6,7]被应用在立体匹配领域来同时达到高精度和实时性,但这类算法对硬件性能和数据集依赖较强,成本较高。Yang[8]提出基于树形结构的非局部匹配算法,解决了全局算法计算效率低,局部算法容易陷入局部最优的问题,但是代价计算阶段只考虑单一的图像信息,图像边缘的匹配精度不高。针对以上方法的不足,本文提出了一种融合颜色、边缘和Census信息的立体匹配代价计算方法,通过自适应窗口获得更优的匹配代价策略,同时提出一种基于图像分割的最小生成树权重策略,计算代价聚合,进一步提高视差精度。该算法能够在对硬件性能和数据集没有明显依赖的条件下,实现高精度立体匹配。
1 匹配代价计算
立体匹配算法的输入为两张存在视差关系(一般为水平视差)的图像,其中一张被称为参考图像(reference image),另一张为目标图像(target image)。匹配代价计算作为立体匹配的第一步,它被用来衡量参考图像和目标图像像素之间的相似程度。由于图像的复杂性,当前的匹配算法在光照变化区域、像素边缘区域的匹配精度较低。针对以上问题,本章提出了一种自适应窗口的融合匹配代价计算方法,其融合了图像颜色信息、Census信息和边缘信息。颜色信息计算简单,对图像细节辨识能力强,但容易受噪声和光照变换的影响;Census信息对光照变化不敏感,鲁棒性高;像素边缘信息复杂,图像特征显著,常处于视差不连续区域,融合边缘信息能减少在边缘上的错误匹配。
1.1 自适应窗口的Census变换
Census变换[9]是一种局部非参数变换,计算存储点在窗口中的灰度顺序和局部邻域的空间结构信息。传统的Census变换流程为:使用一个固定大小的矩形窗口遍历图像,比较像素邻域内的局部灰度差异并将比较后的差异大小转换成比特串,最后根据比特串计算左右图像像素对的Hamming距离,作为匹配代价,衡量图像之间的相似度。Census变换公式为
(1)
式中:I(p)、I(q)为像素点p,q的灰度值,⊗为位串联符,W′(p)是W(p)内除中心像素点p外的邻域点集。ζ表示按位比较,满足
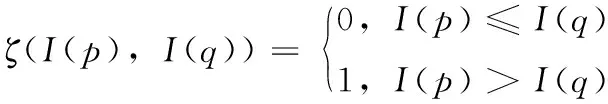
(2)
将Census变换得到的比特串,计算Hamming距离作为匹配代价,Hamming距离越小,则代表两个像素点间的相似度越高,也就是匹配代价越低。Hamming公式为
CCensus(p,d)=TCensus(p)⊕TCensus(p+d)
(3)
式中:TCensus(p)和TCensus(p+d)分别表示参考图像和目标图像中视差值为d的Census变换值。
由于传统的Census变换依赖于固定矩形窗大小的选择,但针对图像不同区域,需要选择不同的窗口策略。在边缘区域,通常需要较小的窗口来进行代价计算,否则会造成图像的模糊;而在非边缘区域选用较大的窗口进行代价计算,能较好反映图像纹理信息。为了提高图像匹配精度,适应不同的图像区域,提出一种基于Sobel边缘检测算子的自适应窗口Census变换算法。
Sobel算子使用两个3×3矩阵作为卷积模版,分别代表横向和纵向。令A为被处理后的图像像素矩阵,Gx和Gy各自为每一个像素横向和纵向的灰度梯度,G为该像素点的灰度梯度,则公式为
(4)
通过Sobel算子检测出像素点的梯度值后,根据计算出的像素边缘大小在不同区域采用不同的窗口尺寸进行Census变换,自适应选用窗口的具体规则如下
(5)
式中:W代表选定的窗口大小,W1,W2分别代表大小不同的窗口。
当像素边缘值G小于等于阈值T时,表明该区域纹理平缓像素信息变化较小应采用大窗口,而在其它边缘深度不连续区域采用小窗口用以保护边缘。图1表示传统Census变换和改进的自适应窗口Census变换得到的视差,如图像中部矩形框所示,在房顶烟囱附近,改进后的Census变换算法图像更加平滑,在右上角弱纹理区域,玩具手部和背景更好的区分开来。因此,改进后的算法具有更好的边缘保持特性,从而匹配精度提高。

图1 传统的Census变换和改进Census变换得到的视差
1.2 多测度融合代价计算
首先对颜色信息进行代价计算。一般情况,左右图中像素颜色越相似,越可能有相近的视差,构造像素p以d为视差值的颜色信息匹配代价CTAD(p,d),公式为
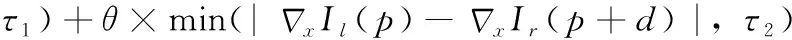
(6)
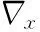
对边缘信息进行代价计算。为了减小计算复杂度,避免重复计算,结合1.1节中的Sobel边缘算子计算得到的边缘值,构造边缘匹配代价CE(p,d),公式为
CE(p,d)=min(|edge(p)-edge(p+d)|,τ3)
(7)
式中:edge(p)函数为像素点p的Sobel值,τ3为截断值。
对Census信息进行代价计算。同式(3)。
先将相同一尺度下的颜色和边缘信息代价融合CR(p,d),公式为
(8)
再将颜色、边缘和Census信息代价融合C(p,d),公式为
C(p,d)=ρ(CR(p,d),λR)+ρ(CCensus(p,d),λCensus)
(9)
式中:ρ(C,λ)是关于变量C的归一化函数,定义为
(10)
2 代价聚合
由于图像中的单个像素点极易受噪声影响,且没有考虑到像素之间的视差值存在一定相互关系,通过初始代价计算后得到的像素视差往往不准确且不连续,所以需要对参考图像中每个像素点进行代价聚合。文献[8]构造了基于最小生成树的代价聚合,但尺度单一,权重仅依赖颜色信息,匹配精度有待提高。针对此问题,本章提出一种基于图像分割的树形滤波代价聚合算法。
2.1 最小生成树的构造
基于图论的树形滤波器,将参考图像视作为一张连通无向图G=(V,E),顶点V为图像的像素点集合,E为边的集合,可以连接图中任意两点。假设图像中两个像素点p,q,连接两点的边的权重表示为w(p,q),其值大小可以衡量相邻像素的相似度,如果∃K∈V且为无圈图,使w(K)最小,则K就称之为G的最小生成树。本节把无向图G看作四连通图,即像素的上、下、左、右是其邻近区域。若仅考虑颜色信息,则权重值w为邻近像素p,q间颜色(R,>G,>B)的最大绝对差
(11)
式中:Ii(p)为像素p在i通道的下的像素值。
在构造无向图时,参照代价计算步骤,将像素的颜色和边缘信息融合计算边权重,有利于提高边缘区域的匹配精度。为了获取图像边缘信息,需要对图像进行分割。本节采用均值漂移(mean-shift)算法进行图像分割,它作为一种聚类算法,收敛快、分割效果好。图2中颜色相同表明分割后位于同一区域。
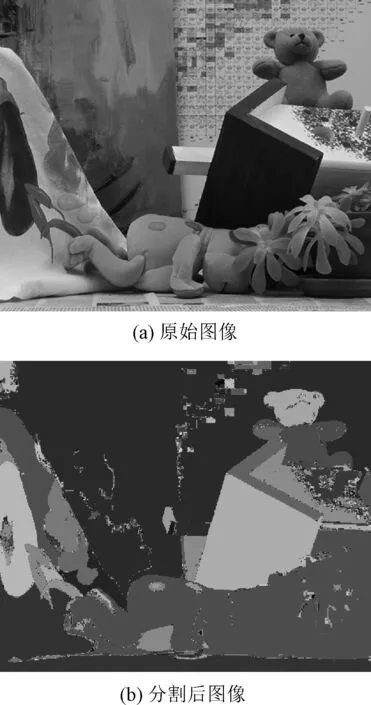
图2 图像分割前后
以分割图像结果为根据,构造新的权重函数
(12)
式中:edge函数为求像素点的Sobel值,α为调节参数,V1,2,3,…,n表示分割后不同颜色区域。
由此可知,在生成最小树的过程中,若两点间差异越大,则连接两点的边上的权重值就会越大,这些边会在求解最小生成树的过程中被删除,最后就会得到一棵由所有像素点构成的最小生成树,这类问题一般用贪心算法求解。
采用有限元软件ABAQUS建立类方形蜂窝夹层结构精细有限元模型,分别对四边简支条件下双壁厚和等壁厚类方形蜂窝夹层结构进行模态分析。模型尺寸如表2所示,夹层结构上、下面板及夹芯材料均采用Al6061,在夹层结构的4个边界处分别施加平行边界方向及z向位移约束,模拟简支边界条件;表3为双壁厚和等壁厚类方形蜂窝夹芯的等效弹性参数。
2.2 最小生成树的代价聚合

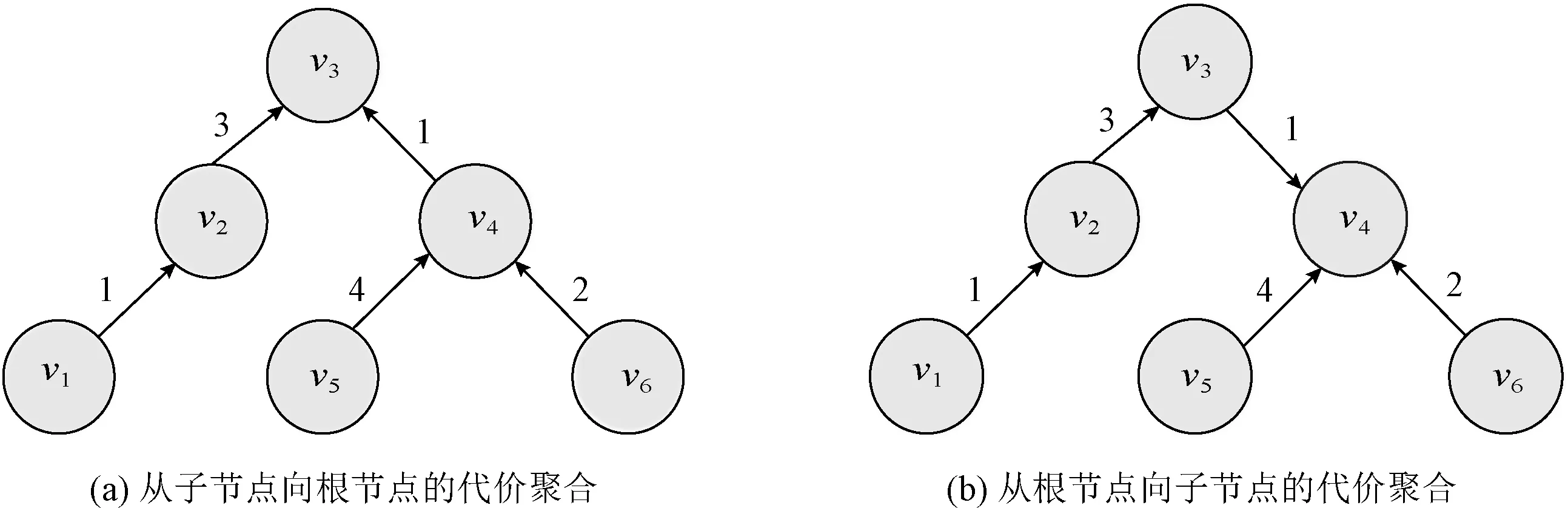
图3 最小生成树上的代价聚合
(13)
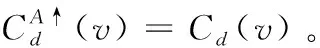
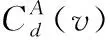
(14)
根据式(14),就可以求得最小生成树中任何一个节点的代价聚合。在代价聚合时,像素节点都直接或间接对其它像素节点的代价聚合产生影响,计算过程中只用进行少量加、减、乘运算,因此能高效地进行代价聚合。
3 视差计算及求精
经过代价聚合步骤后,真实匹配点在众多候选点之中的匹配代价最小,于是采用赢者通吃(winner-takes-all,WTA)策略,选取匹配代价最小对应的视差值作为初始视差,得到初始视差图
(15)
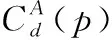
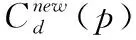
(16)
把不稳定点的匹配代价值设为0。最后重复第三步代价聚合算法,使视差值从稳定点扩散到不稳定点,令图像平滑,再次利用WTA策略得到精确视差图。
综上,本文算法流程如图4所示。
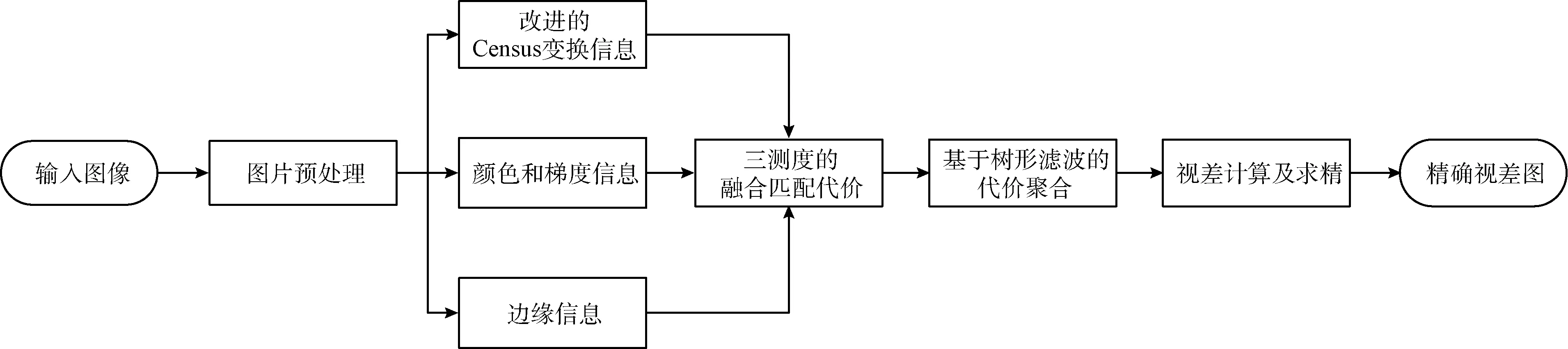
图4 本文算法流程
4 实验结果与分析
为验证本文算法的有效性,在本节中,将本文算法与它4种算法作比较:图割算法[10](graph cut,GC)、半全局匹配算法[11](semi-global matching,SGM)、同样基于树形结构非局部代价聚合算法[8](non-local cost aggregation,NLCA)及其改进的分割树算法[12](segment-tree,ST),其参数按照相应论文设置。并选取Middlebury网站平台[13]中的图像作为测试集,其中标准数据集Tsukuba、Venus、Teddy和Cones,4组图像的视差搜索范围依次分别为[0,15]、[0,>19]、[0,>59]和[0,>59]。实验使用的电脑配置为Windows 10 64位系统,8 GB内存2 GHz AMD处理器,使用C++语言在Visual Studio 2013和OpenCV 2.4.9平台上实现算法。
对于定量评价指标的计算,将算法所得视差图与真实视差图作比较,计算视差值大于给定视差阈值的像素点占整体视差图像素点的比例,即误匹配率PBM(percentage of bad matching),公式为
(17)
式中,dc(p)为计算所得的视差值,dt(p)为图像真实视差值,N为图像像素点总数,δd为视差阈值,一般情况下取1。
为了测试算法在Middlebury测试集中的图像不同区域的具体表现,将测试图像划分为视差不连续区域和非遮挡区域,统计结果Disc、All、Nonocc分别代表视差不连续区域、全部区域和非遮挡区域的误匹配率。
实验中使用的参数值见表1。其中,参数α调节式(12)代价聚合时最小生成树边的权重w,α越大表示边缘信息的贡献越大,反之,颜色信息的贡献越大。为了找到一个通用且合理的α值,使图像的匹配精度最高,对α在[0,1]的范围内,计算4个标准的Middlebury数据集在全部区域上的误匹配率。实验结果如图5所示,当α取0.1时,匹配效果最优,平均误匹配率最小。

表1 参数列表
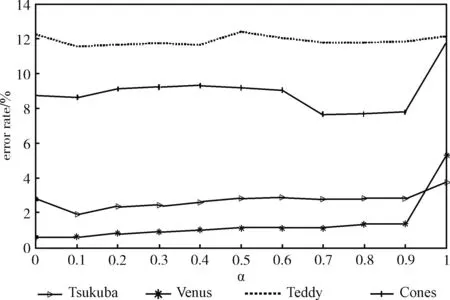
图5 不同α取值下的误匹配率
在Middlebury 4个标准测试集上的实验结果如图6所示。图6(d)误差图中黑色部分为误差区域,黑色部分越少表示匹配精度越高,可以看出算法比较接近于真实视差图。同时将本文算法与其余4种算法在Middlebury标准测试集上定性分析,得到的视差图对比情况如图7所示。因为本文算法对边缘信息上的关注,在低纹理区域、视差不连续区域都要表现出更优的匹配效果。在标准图Tsukuba中,用白色矩形框框出台灯区域,其属于视差不连续区域,可以看出,本文算法比NLCA和ST算法在台灯边缘轮廓上显示更加清晰;还有Teddy图中,矩形框内为弱纹理区域,本文算法与NLCA算法效果相当,很好地将玩具的手部与背景区分,手部轮廓显示清晰;对于Cones图中矩形框内的重复纹理区域,为本文算法能较好得将重复区域区分开来,与真实视差图更为接近。

图6 本文算法结果与真实视差对比

图7 算法视差结果
除了视觉上的定性分析,也需要从数据上来定量分析。表2为各算法在4组不同风格的标准集上定量评价结果,视差阈值为1, 使用视差不连续区域,全部区域和非遮挡区域的误匹配率来评估该算法的性能。如表2所示,本文算法在各区域的误匹配率都低于其它算法,在平均误匹配率上,本文算法比NLCA和ST算法提高了2个百分点,是SGM算法的3.37倍。

表2 算法误差率对比/%
为了获得更可靠的算法评价,在Middlebury 2005和2006测试集中选取16组数据集来测试算法的性能,这里使用非遮挡区域的误匹配率来进行比较,表3为定量评价的结果。本文算法以最低的平均误匹配率和最高的平均排名优于其它算法。从本文算法的定量结果可以看出,非局部的树形滤波算法从边缘和分割信息中获益匪浅。同时,为了更直观的比较,这里将Cloth3和Dolls的视差图结果展示在图8中。与ST和NLCA算法相比,本文算法在弱纹理区域和像素边缘区域有较好表现。

图8 算法在Cloth3和Dolls数据集上的视差结果

表3 算法在非遮挡区域误差率对比/%
算法的运算时间见表4,由于本文算法在计算匹配代价时,边缘信息由自适应选择Census变换窗口,计算比较耗时,相较于只考虑颜色信息的NLCA和ST算法,速度稍慢。但是在代价聚合时,算法时间相当。后期可以考虑使用并行计算,以降低代价计算所耗时间,进一步提高匹配速度,达到实时性。
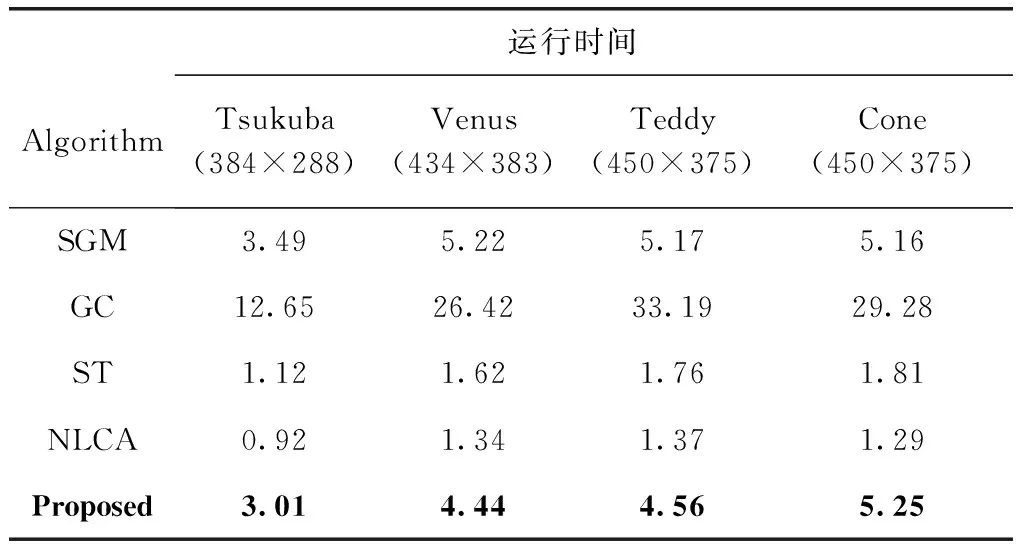
表4 算法运行时间对比/s
5 结束语
针对立体匹配算法中的代价计算和代价聚合步骤,本文提出一种高精度的立体匹配算法。在代价计算阶段,本文算法自适应选择Census变换窗口,将边缘信息融合进代价计算中来,使代价函数中包含了更加完整的图像信息,减少误匹配率。在代价聚合阶段,基于树形结构构造以边缘信息和颜色信息为权重值的最小生成树,通过树形滤波器进行初始代价聚合。采用WTA策略进行视差后处理,生成视差图。实验结果表明,与同类算法相比,本文算法在低纹理区域、遮挡区域和视差不连续区域匹配精度均高于其它算法,同时有较好的边缘保持特性。

