基于有限元技术的仪表板综合特性评估及结构轻量化
黄海彬
(南昌航空大学科技学院,南昌 330034)
仪表板是汽车内饰中比较重要、工艺复杂的部件,各种仪表、电子设备和控制开关等均安装在其总成上,主要通过仪表板横梁安装于驾驶室内部前端,在高接触和高可见位置,直接影响驾乘人员的视觉感受。当车辆行驶时,车身会受到动载荷的作用而引起仪表板振动,当动载荷频率与仪表板固有频率接近时,则会产生共振,从而影响车辆的舒适性。与此同时,仪表板需具备良好的刚、强度特性,以保证其在静、动载荷作用下能够抵抗一定的冲击,因此汽车仪表板的综合特性显得尤为重要。
目前众多学者通常只针对仪表板的某一项或两项特性进行分析,王协庭[1]采用有限元技术对某仪表板的刚度性能和模态性能进行仿真分析,并对其进行评估。查勇岗等[2]基于尺寸和形状优化方法对某仪表板横梁的结构参数进行优化设计,优化之后其质量减轻了19.3%。黄伟[3]通过对某仪表板进行网格离散化处理,再进行模态分析和频率响应强度分析,发现结构优化之后仪表板模态频率增大,同时其强度应力值减小。马其华等[4]对某仪表板进行了振动特性分析和刚度特性分析,并且基于灵敏度和优化方法对其进行轻量化设计,最终实现了减重12%的目标。N. A. Haniffah等[5]采用有限元方法对某仪表板进行强度分析和结构优化,提升了其安全系数。Li Chao等[6]基于拓扑、尺寸和形状优化等方法对某汽车仪表板横梁进行优化,最后达到了减重40%的目标。
目前针对汽车仪表板的性能分析通常很少兼顾其各项静、动态特性。为了综合考虑仪表板各项性能,笔者首先基于有限元方法建立仪表板总成网格模型,并进行模态特性仿真分析,获取其固有频率及阵型;然后基于3倍重力加速度对其进行振动强度特性仿真分析,获取其应力水平,该方法能够真实地反映仪表板使用工况;再基于额定载荷对其进行抗凹特性分析,获取仪表板各个区域的变形值,由此获取了仪表板的模态特性、振动强度特性和抗凹特性,能够综合评估仪表板的各项特性。第二代非劣排序遗传算法具有搜索能力强、计算效率高等特点,因此最后笔者基于该算法对仪表板进行了轻量化设计,以获得综合性能与轻量化效果均为优异的汽车仪表板。
1 仪表板模态特性评估
1.1 振动基础理论
结构的运动均由自由振动的模态组成,模态分析的基本原理是将结构简化成若干个自由度同时没有外部激励的模态矢量方程,结构阻尼对模态特性影响比较小,因此结构的无阻尼振动方程为[7–8]:

式中:[M]——质量矩阵;
[K]——刚度矩阵;
{ü}——加速度向量;
{u}——位移向量。
式(1)的解为:
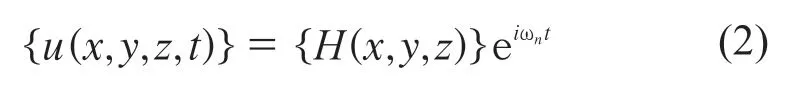
式中:x——结构的纵向;
y——结构的横向;
z——结构的垂向;
t——时间;
H(x,y,z)——结构位移矢量的幅值;
ωn——结构角频率。
由此得到:

式(3)中,k为阻尼,式(3)存在非零解,由此得到[K–kn
2M]=0。

式中:λi——结构的第i个特征值;
Hi——结构的第i个特征矢量。
通过式(4)即可获取结构的模态特性。
1.2 仪表板离散化模型
某车型仪表板为相对比较复杂的注塑部件,其主要材料为聚碳酸酯/丙烯腈-丁二烯-苯乙烯塑料共混物,质量共计为19.8 kg。为了确保仪表板分析的精确度,有限元网格模型必须真实地表征其几何特性和力学传递关系,并且应当尽量减小求解时间,提升计算效率。采用Catia软件创建该仪表板数字模型,同时加载至Hypermesh软件[9–10],再抽取其中性面,并进行表面清理,比如补齐缺失面、删除小圆孔和小倒角等。在有限元网格离散化过程中,虽然三角形单元比较灵活,但是精确度不高,而四边形单元能够保证准确性。因此为了兼顾分析的准确性和计算经济性,基于5 mm×5 mm均匀的四边形单元进行网格离散化,复杂和过渡区域允许产生小部分三角形单元。仪表板的各个零部件之间的螺钉和卡扣连接均采用刚性单元代替,其材料均设置为线性弹性属性,以此建立仪表板网格模型,如图1所示,图1中T1~T9代表仪表板主要部位的厚度值,其中T1为前挡板厚度值,T2为顶部挡板厚度值,T3为中间挡板厚度值,T4为左侧挡板厚度值,T5为手套箱厚度值,T6为右侧挡板厚度值,T7为中央控制器挡板厚度值,T8为右膝挡板厚度值,T9为左膝挡板厚度值;P1~P12为仪表板上强度相对较低的位置,其中P1为前挡板右点,P2为顶部挡板右点,P3为顶部挡板中间点,P4为顶部挡板左点,P5为右侧挡板右点,P6为右侧挡板左点,P7为中间挡板中点,P8为左侧挡板中点,P9为手套箱中点,P10为右膝挡板右点,P11为左膝挡板左点,P12右膝挡板中点。
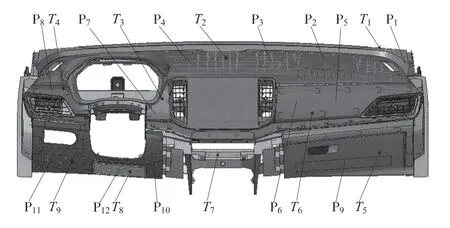
图1 仪表板网格模型
1.3 模态特性结果
仪表板分别通过螺钉、定位销和螺栓与车身、地板连接,因此基于仪表板网格模型,采用Nastran软件[11–12]约束相应螺钉和螺栓连接的全部自由度,约束相应定位销的三向平动自由度,基于EIGRL卡片设置其频率提取范围为1~60 Hz (低阶频率对其模态特性影响比较大),获取该乘用车仪表板的前三阶模态频率分别为38.4,45.2 Hz和58.6 Hz,其对应的阵型分别如图2~图4所示。由图2可知,仪表板的第一阶阵型表征为整体弯曲,其最大振动量相对比值为34.53 mm,阵型比较平滑。由图3可知,仪表板的第二阶阵型表征为手套箱凸起,其最大振动量相对比值为53.1 mm,阵型也比较平滑。由图4可知,仪表板的第三阶阵型表征为膝部挡板扭动,其最大振动量相对比值为81.96 mm,阵型未发生畸变。
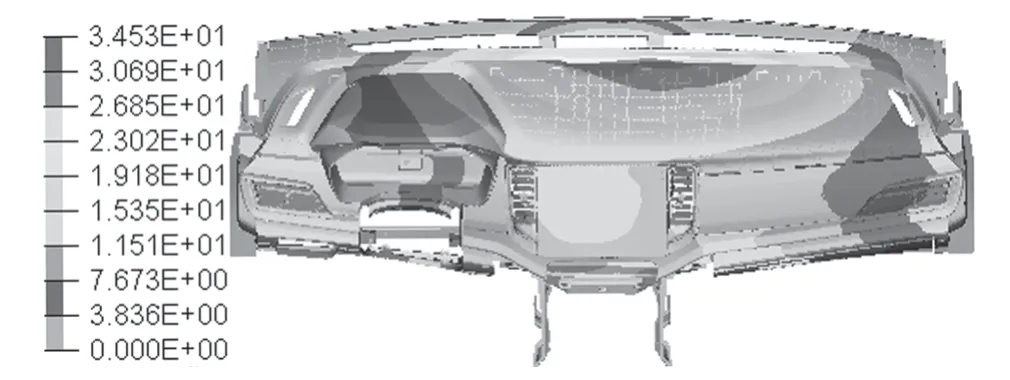
图2 仪表板第一阶阵型

图3 仪表板第二阶阵型

图4 仪表板第三阶阵型
仪表板在汽车行驶过程中,主要承受发动机和路面的激励作用。路面激励频率范围处于10~20 Hz,发动机怠速为800 r/min,基于理论公式得到发动机的共振频率为30 Hz。设定仪表板的模态特性的安全系数为1.2 (要求频率大于36 Hz),因此该仪表板的固有频率均超过了发动机和路面的激励频率,不会发生耦合共振风险,能够最大限度地避免产生异响和振动,满足模态特性设计要求。
2 仪表板振动强度特性评估
仪表板需要承受来自各种复杂路面的振动激励,因此其必须具备足够的强度以避免发生开裂失效。车辆在恶劣路况时,仪表板将承受3倍的重力加速度,该动态强度工况相比静态受压工况,能够真实地反映仪表板在车辆行驶过程的受力关系,因此基于仪表板的网格模型,设置与模态特性分析相同的约束条件,采用GRAV卡片定义3倍的–Z方向重力加速度,输出应力和位移,以此对其进行振动强度特性仿真分析,获取该仪表板在振动状态的应力分布情况。图5为仪表板变形云图。由图5可知,仪表板的最大位移为0.6206 mm,处于仪表板的上端,小于工程要求值(2 mm),其刚度性能比较良好。图6为仪表板在振动状态下的应力分布云图。由图6可知,仪表板的最大振动应力为25.75 MPa,位于中控横梁位置,低于材料阀值(50 MPa),振动强度安全系数为1.94,因此具有较好的振动强度特性和优化空间。

图5 仪表板变形云图

图6 仪表板振动应力分布云图
3 仪表板抗凹特性评估
由于仪表板处于高接触区域,容易受到外界载荷的作用,因此必须具备良好的抗凹特性。约束仪表板与车身、地板连接位置的所有自由度,在仪表板外侧区域选取12个如图1所示的相对薄弱的位置P1~P12。在各个位置的垂直方向添加直径为15 mm的刚性体,并建立局部坐标系,只释放垂向的平动自由度,约束其它方向的平动和转动。在参考点加载大小为25 N的垂向力,刚性体与各个区域建立通用接触对,摩擦系数为0.15,以此进行抗凹特性仿真分析。以P3,P6,P9和P12位置为例,分析这几个位置受压时的变形云图,结果分别如图7、图8、图9和图10所示。由图7可以看出,仪表板P3位置受压时最大变形量达到了0.6691 mm,低于目标值(2 mm),能够抵抗一定的变形,满足抗凹特性要求。由图8可以看出,仪表板P6位置受压时最大变形量达到了0.4511 mm,小于2 mm,满足抗凹变形要求。由图9可以看出,仪表板P9位置受压时最大变形量是1.052 mm,也低于2 mm,刚度性能比较良好。由图10可以看出,仪表板P12位置受压时最大变形量达到了2.147 mm,超过了2 mm,其抗凹特性不符合设计要求,存在一定的风险,可能会影响仪表板的功能性。

图7 仪表板P3位置受压时变形云图

图8 仪表板P6位置受压时变形云图

图9 仪表板P9位置受压时变形云图

图10 仪表板P12位置受压时变形云图
表1为该乘用车仪表板在各个加载位置受压时的变形值。由表1可知,仪表板P1~P11位置在受压时的最大位移均小于2 mm,但P12位置的变形值大于目标值,不满足抗凹性能要求,需要对其进行局部优化,以改善其抵抗变形的能力。

表1 仪表板各个位置的变形值 mm
4 仪表板结构的轻量化
4.1 优化方法
仪表板P12位置属于膝部挡板处,该位置为高接触区域,经常受到膝部的磕碰。为了提升该区域的抗凹性能,需增加其局部的刚度,因此在挡板背面增加三条横加强筋和四条竖加强筋,如图11所示。

图11 局部增加加强筋
仪表板的模态特性和振动强度特性良好,并且仪表板的轻量化有利于减轻车辆的质量,能够有效提升车辆的动力性,因此将仪表板主要部位的厚度值(图1的T1~T9)作为设计参数,采用Isight软件导入仪表板网格模型的命令流,并且参数化其各个厚度值,并设置为输入变量。同时加载仪表板模态特性分析、振动强度特性分析和抗凹特性分析的命令流,将仪表板的质量、第一阶模态频率、最大应力值和最大变形值均设置为输出参数,将仪表板的质量最小定义为目标响应,以仪表板的第一模态阶频率大于36 Hz、最大振动应力值小于50 MPa、静态最大变形值小于2 mm作为约束函数。
第二代非劣排序遗传算法[13–14]具有搜索能力强、计算效率高、收敛性好等优势。其在目标区域内根据最佳关系将个体参照目标值进行相互对比,再将全部个体划分成多个前沿层,使得其探索能力倍增,因此基于该算法对其进行结构优化。设置该算法的种群规模为20,最大迭代次数为200,交叉的概率为0.9,交叉分布指数为10。
4.2 轻量化结果
通过系统多轮优化分析,最终得到仪表板主要部位厚度的最佳参数见表2。由表2可知,仪表板主要部件的厚度值较优化之前均有所减薄,并且结构轻量化后仪表板的质量达到了16.9 kg,较优化之前降低了14.6%,轻量化效果比较理想,能够有效减轻仪表板总成的质量,以此提升车辆的燃油经济性。
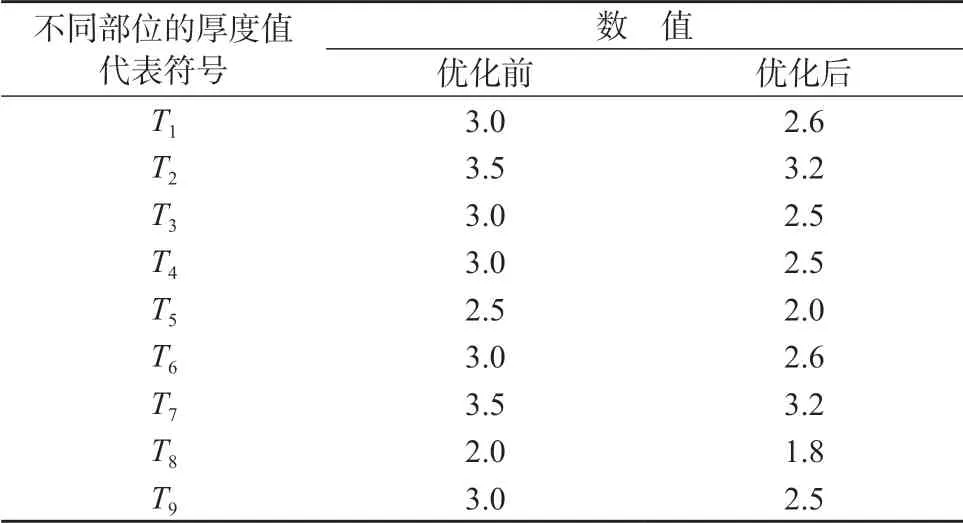
表2 结构轻量化前后的不同部位的厚度值 mm
图12为结构轻量化后仪表板P12位置受压时的变形云图。由图12可知,结构轻量化后其受压时的最大变形量达到了1.894 mm,低于工程目标值,符合抗凹特性标准。

图12 结构轻量化后仪表板P12位置受压变形云图
图13为结构轻量化后仪表板第一阶阵型。由图13可知,结构轻量化后的第一阶阵型仍然为整体弯曲,其最大相对振幅值达到了28.25 mm,并且其第一阶模态频率为36.7 Hz,仍然处于发动机和复杂路面的激励范围之外,符合振动特性要求。

图13 结构轻量化后仪表板第一阶阵型
图14为结构轻量化后仪表板振动应力分布云图。由图14可知,结构轻量化后最大振动应力达到了30.43 MPa,其振动强度安全系数达到了1.64,因此强度性能比较优良,能够避免后期发生开裂,符合客户使用要求。

图14 结构轻量化后仪表板振动应力分布云图
5 结论
(1)基于有限元方法并采用Hypermesh软件构建仪表板离散化模型,根据实际装配情况约束各个自由度,对其进行模态特性仿真分析,获取其前三阶模态频率分别是38.4,45.2 Hz和58.6 Hz,不会与发动机和路面激励重合,满足动态属性要求。
(2)基于3倍重力加速度对仪表板进行动态强度特性仿真分析,得到其最大振动应力值为25.75 MPa,具有较高的振动安全系数,最大变形为0.6206 mm,能够抵抗一定的变形能力,符合强度特性要求。
(3)在仪表板外侧选取12个相对比较薄弱位置,在其垂向加载相应的载荷,获取其最大位移量为2.147 mm,超过了目标要求值,不符合抗凹特性要求。
(4)基于模态特性、强度特性和抗凹特性分析结果,采用第二代非劣排序遗传算法对仪表板主要部位的厚度进行结构优化,最终获取了其最佳结构,优化之后其综合特性满足设计标准,同时仪表板的质量减轻了14.6%,达到了轻量化的效果。

