基于改进DPNN的矿用运输机故障预测模型构建及仿真
马月连,赵加庆
(1.山东科技大学能源与矿业工程学院,山东 青岛 266590)
(2.江南大学机械工程学院,江苏 无锡 214122)
矿用运输机作为矿井运输的主要设备,其可靠性和安全性直接影响矿业企业的经济效益,更关乎整个矿井作业的安全。高效、准确的故障预测有利于确保矿用运输机的可靠性和安全性。传统机械设备故障预测模型包括灰色关联模型、模糊聚类、马尔可夫链等[1-3],这些模型虽在一定程度上提高了故障诊断效果,但诊断效率和准确性还有待提高。而作为主要预测模型的神经网络,则很少被应用到机械故障预测中。究其原因,岳有军等[4]认为,传统神经网络的容错能力不强,泛化能力差,且在实际应用中只能对单一参量进行预测。中国工程院院士何新贵教授提出的过程神经网络(probabilistic neural networks,PNN)通过神经元可实现输出函数时间与空间的累积,进而实现多参量预测。基于多参量输出优势,PNN算法被广泛应用在故障诊断、检测识别等领域。DPNN(dynamic probabilistic neural network)作为PNN应用的典型,可有效处理矿用运输机为代表的离散型数据,但参数的选择对DPNN算法精度有很大影响。董晓璇等[5]针对DPNN神经网络的优化,提出用粒子群优化(particle swarm optimization,PSO)算法对网络参数进行优化,但PSO算法容易陷入局部最优,导致DPNN神经网络的优化精度不高。本文在上述研究的基础上,提出了改进的DPNN网络矿用运输机故障预测模型,并通过仿真进行对比。
1 DPNN神经网络简介
图1为离散型DPNN神经网络结构。其中,xi(ts)=(x1(ts),x2(ts),…,xn(ts)),i=1,2…,n,为输入层的状态参数,ts为第s次监测结果;ωij(ts)为第s次测量的状态参数对隐藏层的连接权值;Σ为加权求和算子;f为隐层神经元激励函数;∑t为时间效应积累算子;g为输出节点激励函数;vji为隐藏层对输出节点的连接权值;y为输出结果。
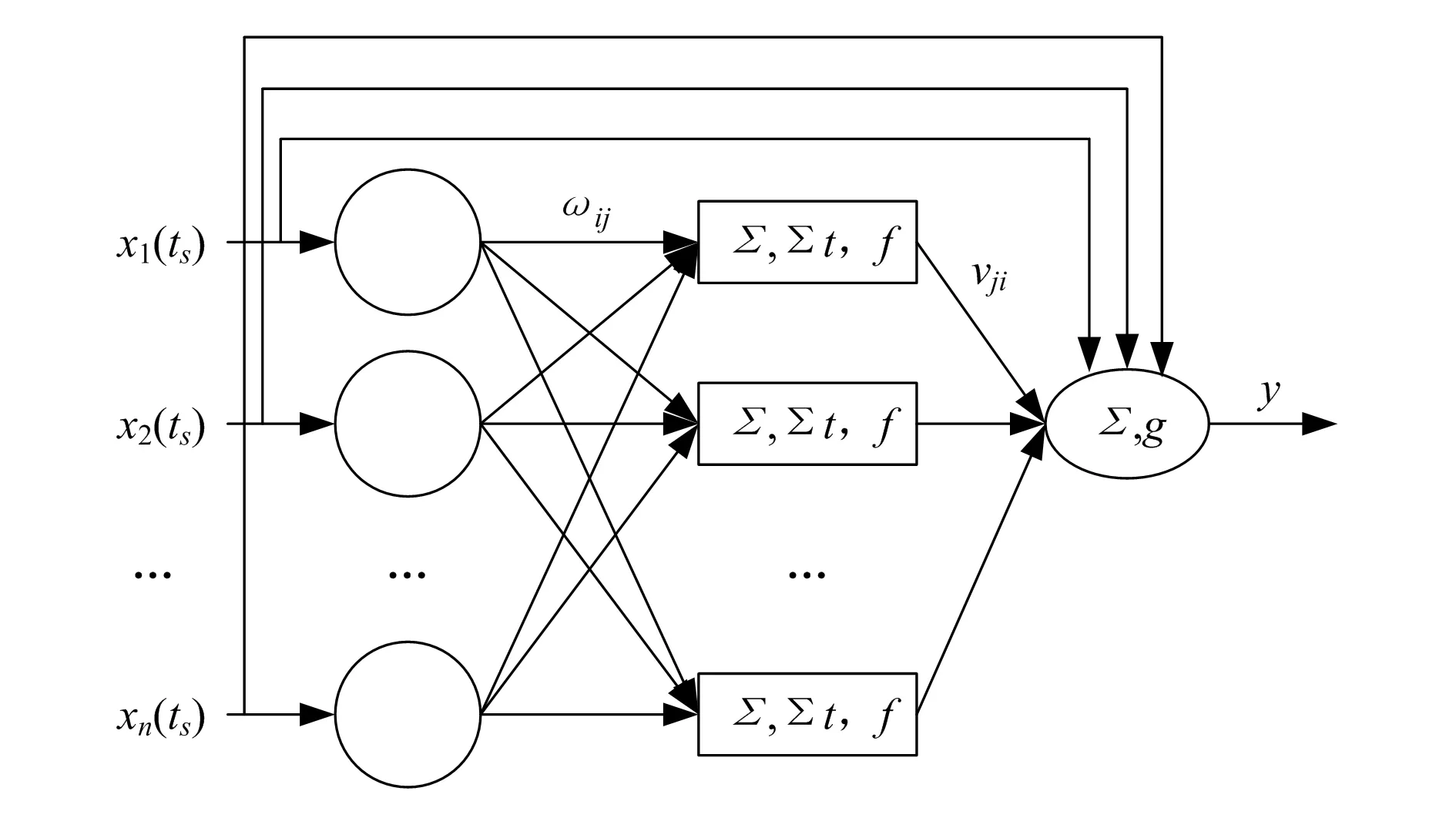
图1 离散型DPNN神经网络结构
设矿用运输机有n个状态输入参数,那么这组状态参数为n维向量,是一组维度为L的时间序列数据。由此DPNN神经网络模型中,时间和空间的聚合效应主要在隐藏层中体现[6-7]。隐藏层节点j对各个状态参数分量的时间聚合效应c(j)与空间聚合效应p(j)分别为:
(1)
(2)
式中:xi(l),ωij(l)分别为维度为l的状态参数以及对应的权值。
为降低计算难度,对ωij(l)进行简化:
(3)
简化后,得到隐含层神经元的输出h为:
(4)
式中:θj为隐含层的激活阈值。
输出层节点q的输出yq为:
(5)
式中:εq为输出层激活阈值。
2 DPNN神经网络参数优化改进
2.1 PSO-LM的参数优化
传统的DPNN神经网络参数优化采用全局寻优能力强的PSO算法,但PSO算法容易陷入局部最优解[8]。鉴于PSO算法的局限性,人们提出各种改进方法,如遗传算法、蚁群算法等。研究认为,LM(Levenberg-Marquardt)算法具有较强的局部收敛能力,且收敛速度较快[9],因此本文充分利用PSO算法和LM算法的优势,提出PSO-LM组合算法对DPNN神经网络参数进行优化。
PSO-LM算法步骤为[8]:
步骤1,初始化PSO算法状态参数,包括粒子初始位置、初始速度、最大迭代次数以及误差精度。
步骤2,按照PSO算法流程初步求得全局最优解,并作为LM算法的初始参数。
步骤3,设置LM算法的最大迭代次数和误差精度。
步骤4,按照LM算法流程寻找全局最优解。
步骤5,判断LM算法得到的全局最优解是否满足要求,若达到最大迭代次数或和方差(SSE)小于误差精度,则结束算法并输出最优解;反之,则返回步骤2。
2.2 权值实时更新改进
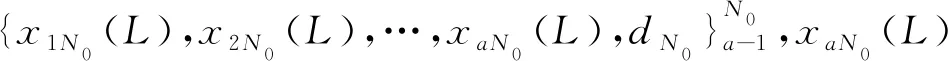
(6)
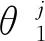
对于N0个样本,式(6)可简化为:
T=H·β
(7)
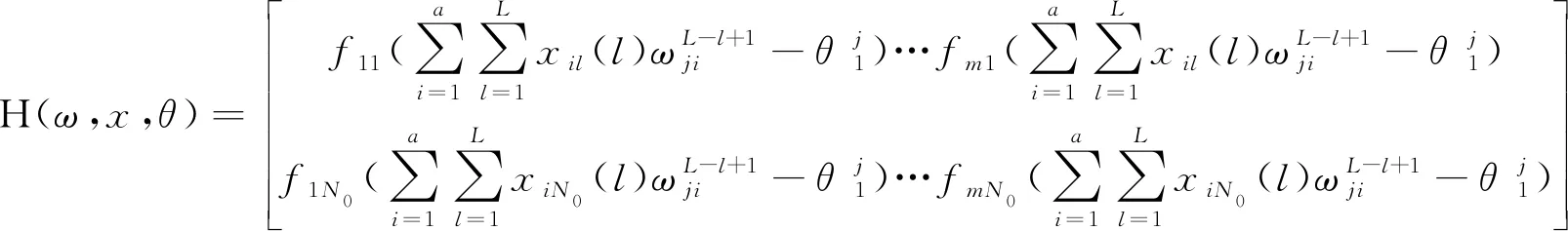
(8)
式中:H(ω,x,θ)为DPNN的隐藏层输出矩阵;T为误差矩阵;fmN0(·)为第N0个样本在m个神经元作用下的输出值;β为权值矩阵。
确定N0个样本后,即可确定矩阵H和T,则问题就转化为求解权值矩阵β。该矩阵可通过线性系统最小范数最小二乘解和Moore-Penrose广义求得,即:
(9)
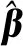
样本更新后,得到新的隐含层到输出层的权值矩阵β0为:
(10)
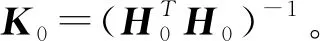
(4)新形势下,医患矛盾突显,关系紧张,医疗纠纷和伤医事件时有发生,医务工作者的精神压力也很大,身心健康问题日益彰显。
(11)
(12)
更新PSO的粒子群体最佳位置,得到:
(13)
以此方式类推,可得第(k+1)次更新Nk+1个样本后的递推矩阵为[11]:
(14)
2.3 基于PSO-LM组合算法的DPNN矿用运输机故障预测模型构建
基于2.1和2.2的优化和改进,构建矿用运输机PSO-LM-DPNN故障状态预测模型,故障状态预测流程如图2所示。
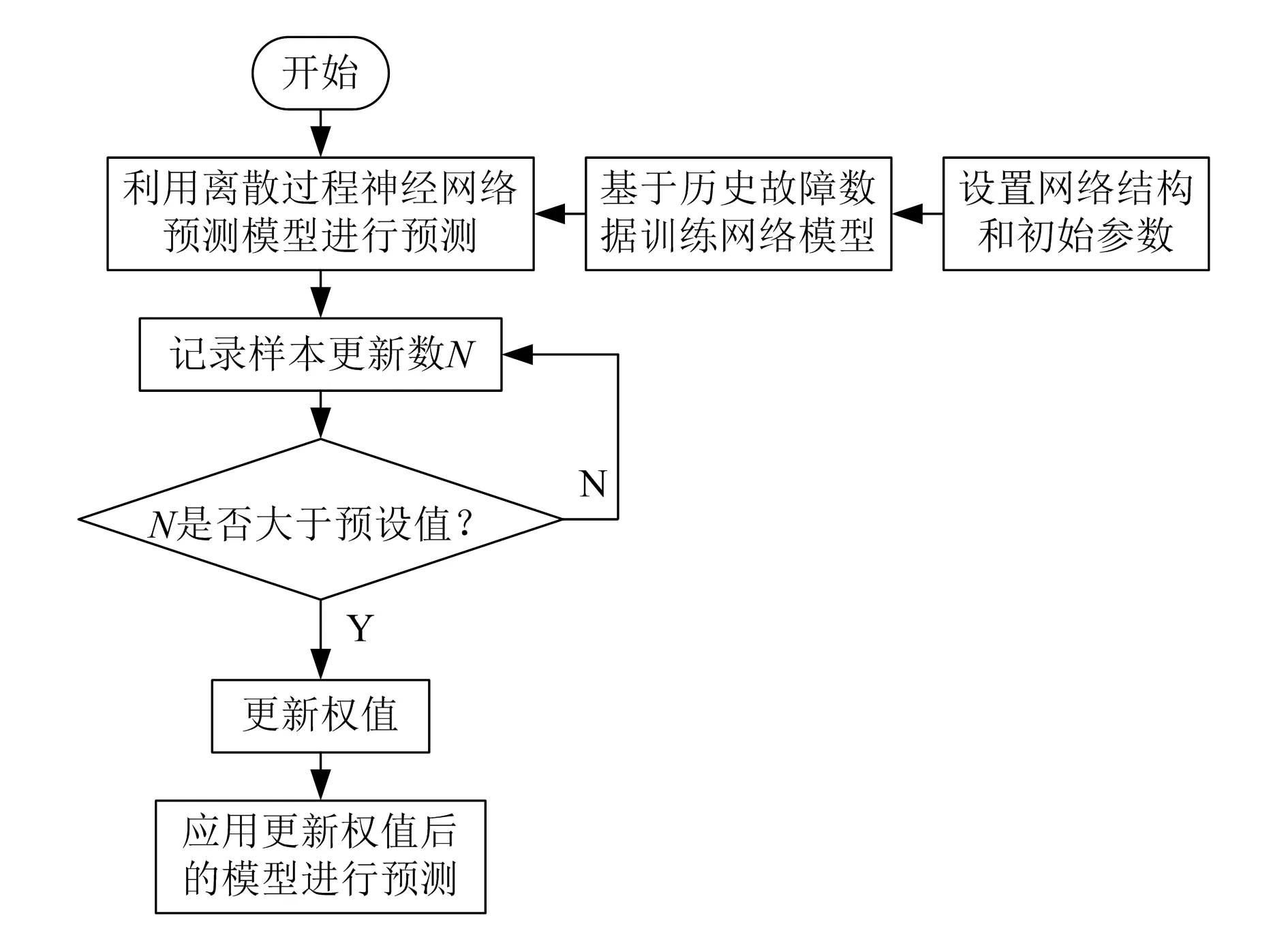
图2 故障状态预测流程
步骤1,模型训练。设置网络结构和初始参数,利用处理得到的历史故障数据对模型进行训练。
步骤2,更新权值。用训练好的网络模型预测状态参数,并记录和更新样本数据。当样本个数为N0时,计算出初始权值矩阵和隐层输出矩阵。
步骤3,重复步骤2,直到权值矩阵更新结束。
步骤4,利用更新权值后的模型进行矿用运输机故障预测。
3 仿真实验
3.1 数据来源与处理
本文实验数据为某实验室矿用运输机的历史运行数据、实时检测数据和故障状态数据,包括驱动滚筒运行速度、滚筒张力、设备关键部位温度和环境湿度。由于矿用运输机数据类型复杂,数据量庞大,存在的干扰数据多,因此在小波阈值去噪的基础上,采用Relief-F算法对矿用运输机故障数据中的参数进行分析。具体步骤如下。
步骤1,数据预处理,确定类别集和属性集,并对确定的属性集和类别集进行编码。根据矿用运输机的运行特点,得到矿用运输机的故障类别集编码为:打滑故障c1、跑偏故障c2、超温故障c3和正常状态c4。属性集编码见表1。
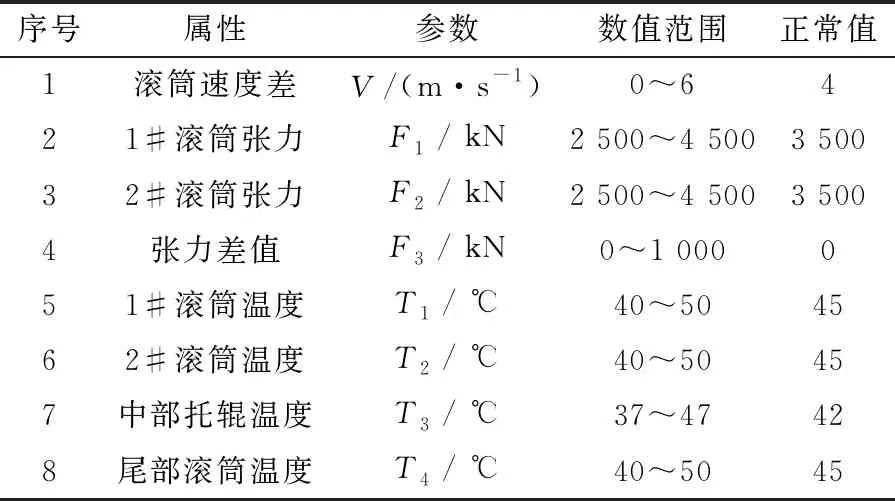
表1 属性集编码
步骤2,数据标准化处理。将所有参数的取值映射到[0,1]内,得到处理后的样本数据见表2。

表2 处理后的样本数据
步骤3,参数权值计算。设取样次数为100,近邻样本数为20,运用Relief-F对表2中各参数的权值进行计算,结果见表3。

表3 各参数权值
步骤4,参数确定。设置阈值为0.1,去除权重小于该值的参数,最终确定矿用运输机故障预测参数为V,F3,T1,T2,T3,T4。
步骤5,数据归一化处理。采用最大值最小值归一方法对表2的样本进行处理,得到处理后的样本数据,具体见表4。
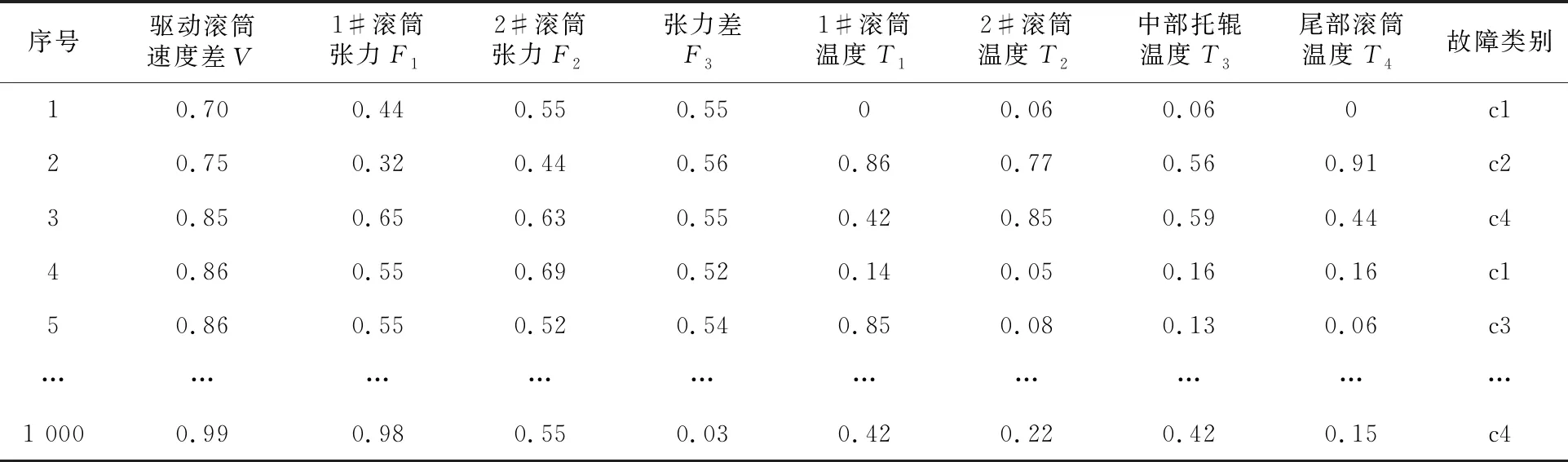
表4 样本归一化处理结果
3.2 预测结果
3.2.1故障预测模型训练结果
为使模型更具普遍性,将DPNN神经网络设计为3层[9],在MATLAB软件中搭建模型。选取sigmoid函数为隐藏层激励函数,输出层激励函数为线性函数,设定输入节点数、输出节点数为6,根据隐藏层节点数参考公式,得隐藏层节点数为16。
首先采用更新权值的PSO-LM算法对DPNN模型进行训练,其中PSO的种群数量为20,PSO的最大迭代数为300,预测模型粗略求解误差精度E1为0.01;LM算法的最大迭代次数为50,精确优化误差精度E2为0.001。
更新网络权值的PSO-LM-DPNN模型训练结果如图3所示。
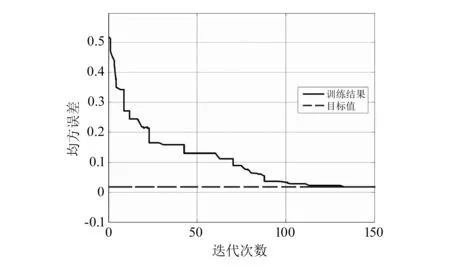
图3 更新权值的PSO-LM-DPNN模型训练结果
为验证更新网络权值的PSO-LM组合算法的有效性,在相同参数条件下,仅采用PSO算法对DPNN模型参数进行优化,得到如图4所示的训练结果。
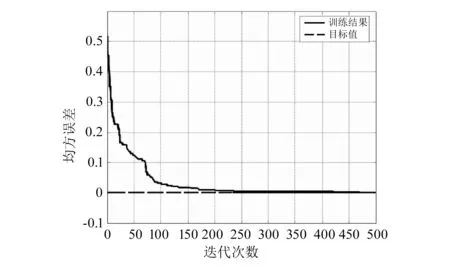
图4 PSO-DPNN训练结果
通过图4与图5的对比可以看出,在满足误差精度为0.001的情况下,PSO-LM组合算法的迭代次数明显少于PSO算法的迭代次数,说明其求解的效率更高。
3.2.2预测结果对比
徐建中等[11]通过研究认为,以连续9个时间序列的参数值对第10个连续时间序列的参数值进行预测,此时预测效果更佳,故以连续9个时间序列的参数组成一个9维的输入向量,预测第10个时间序列参数的输出值。本文选取100个连续时间样本,当每次输入的样本数量达到10组时,更新一次权值。同时为验证更新网络权值算法在提高预测模型精度方面的优势,基于以上同样的试验数据,采用未更新网络权值的PSO-LM、PSO对DPNN参数进行优化,并通过DPNN对数据进行预测,得到滚筒速度差预测结果,具体见表5。
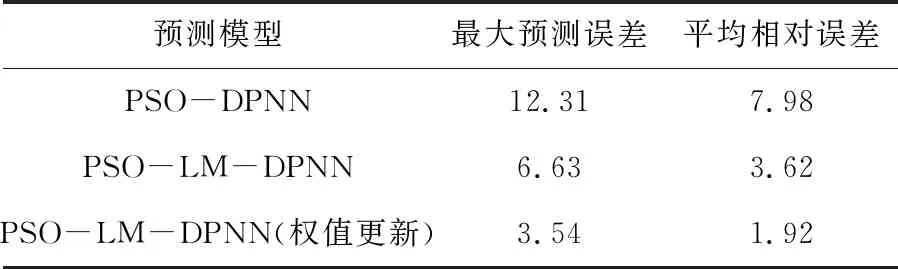
表5 不同DPNN的滚筒速度差预测结果 %
由表5可知,采用网络权值更新的PSO-LM组合算法得到的速度差预测精度最高,误差仅为1.92%,PSO算法的预测精度最低,误差达到7.98%。由此可以看出,本文提出的采用网络权值更新的PSO-LM组合算法在预测精度方面更具优越性。
4 结束语
本文根据矿用运输机故障数据的特点,构建了基于网络权值更新的矿用运输机故障预测模型,并通过仿真进行了验证,结果显示PSO-LM组合算法(权值更新)最大预测误差和平均相对误差均低于PSO算法和 PSO-LM算法,其预测值更接近实际值。本文提出的基于网络权值更新的矿用运输机故障预测模型,能准确预测矿用运输机故障,具有一定的可靠性和有效性,可用于实际矿用运输机的故障预测。

