基于蜻蜓寻优算法的梯级水电站短期优化调度方式研究

晋 健， 刘 育， 王 勇 飞， 李 基 栋

(1. 国能大渡河大数据服务有限公司，四川 成都 610041；2. 国能大渡河流域水电开发有限公司，四川 成都 610041；3. 四川农业大学 水利水电学院 ，四川 雅安 625014)

1 概 述

梯级水库的联合优化调度对保障梯级水电系统安全稳定运行、提高梯级整体效益、确保水能资源的充分利用等意义重大[1]。在梯级联合优化调度问题的研究中，以日为时间尺度的优化调度方式决定了中长期调度战略在每一日的具体执行方式，对于梯级水电站综合效益的发挥十分关键。在确定梯级电站的日内运行方式中，建立面向各种复杂因素的日内短期优化调度模型，再应用各类优化算法进行模型求解成为了研究的常规手段。虽然众多专家学者对短期优化调度问题展开了大量研究，但是模型求解中仍存在计算效率与优化计算效果无法兼顾的问题[2]。

梯级水电系统优化调度模型是一个典型的高维、非线性的优化问题，模型求解十分复杂。此外，由于水流流达时间的存在，短期优化调度问题涉及到日内梯级站间的跨时段水量平衡以及跨日的水量耦合问题[3]，因此短期优化调度模型的求解更具复杂性[4]。目前常规的用于短期优化调度模型的计算方法分为两大类：一类是以传统动态规划为基础的逐步优化算法、逐次逼近动态规划和离散微分动态规划等，这类计算方法普遍收敛速度较慢，且优化计算效果对初始可行解的依赖性较大，普遍计算时间较长[5]。另一类是以遗传算法、粒子群算法、差分进化等为代表的智能型算法，这类方法通常具有求解速度快、效率高的优势，但其计算过程容易陷入局部最优解，或多次计算结果不一致[6]。尽管目前针对各类方法的改进与应用研究较多，各类计算方法在其理论与应用方面都具有各自的特点与局限性，但在实际的工程应用中通常具有一定的限制。

蜻蜓算法(DA)是近年提出的仿生学智能型算法[7]，该研究系统梳理了蜻蜓智能优化算法的计算原理与方法，通过增加局部审查判定、初始种群个体进化等适应性调整，探索蜻蜓算法在梯级水电短期优化调度中的应用，以期丰富水电优化调度方法学，为优化调度计算提供更多的方案。

2 梯级水电站短期调度数学模型

2.1 目标函数

根据水能计算原理，追求梯级整体发电量最大目标函数可以表示为(1)：

(1)

式中Qfi,t为电站i在时段t的发电流量(m3/s)；Mt为时段t的长度(s)；T为调度期内计算总时段个数；N为梯级电站总数；WRi,h为第i个电站水位为h时的平均耗水率(m3/kWh)，该值是一个基于电站历史运行状况率定得到的统计值。

2.2 约束条件

(1)考虑滞时的水量平衡约束。

Qi,t=qi,t+Qi-1,t-γ+(Gi,t-1-Gi,t)/Δt

(2)

式中Gi,t-1、Gi,t分别代表电站i在t时段初、末蓄水量(m3)；qi,t、γ分别表示电站i与电站i-1的t时段区间汇流量和水流滞时；Qi-1,t-γ表示上游电站i-1在t-γ时段的下泄流量。

(2)电站出力限制。

Pi,tmin≤Pi,t≤Pi,tmax

(3)

式中Pi,t max、Pi,t min分别表示电站i的出力上下限制。

(3)水库蓄水量约束。

Gi,tmin≤Gi,t≤Gi,tmax

(4)

式中Gi,t min、Gi,t max分别表示电站i的蓄水量大小限制。

(4)电站出力综合爬坡约束。

ΔPi,t≤CPi

(5)

式中CPi为电站i的出力爬坡率限制；ΔPi,t为电站在时段t的出力变化幅度。

(5)变量非负约束。

上述所有变量均为非负变量。

3 蜻蜓仿生寻优算法

蜻蜓算法寻优计算主要思路通过模拟蜻蜓的捕食行为来实现(图1)，该飞行(进化)寻优机制可以表示为蜻蜓群体分离、对齐、聚集、食物吸引与天敌驱散五个步骤[8]。

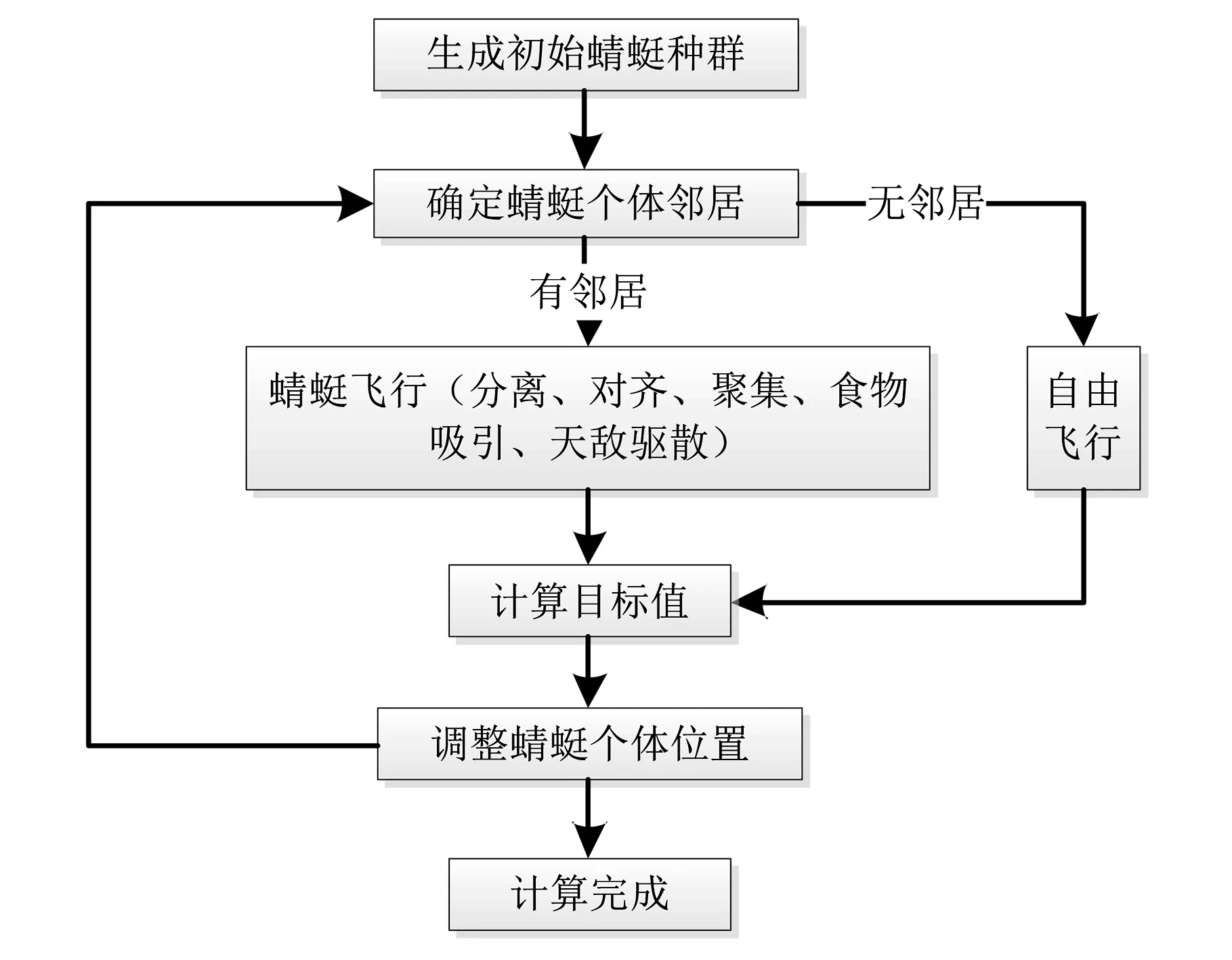
图1 蜻蜓算法寻优计算主要思路

(1)分 离。表示避免蜻蜓个体距离太近降低寻优效率：

(6)

式中Ek为蜻蜓k的分离度；D表示当前蜻蜓的位置；Dj代表第j个邻近蜻蜓的位置；J代表群体中第k个蜻蜓的邻近蜻蜓的数量。

(2)对 齐。表示某个蜻蜓与其邻近蜻蜓个体速度的相同程度：

(7)

式中Uk为蜻蜓k的对齐度；Vj代表第j个邻近蜻蜓的飞行速度；其他符号意义同前。

(3)聚 集。表示某个蜻蜓具有朝着其附近较优蜻蜓个体靠近的趋势：

(8)

式中Bk为蜻蜓k的聚集度；其他符号意义同前。

(4)食物吸引。食物是指某一次迭代计算中最优个体的位置：

Sk=D+-D

(9)

式中Sk为蜻蜓k的食物吸引度；D+代表当前计算中最优蜻蜓的位置。

(5)天敌驱散。目的是使个体尽可能远离最差的蜻蜓个体，提高寻优计算效率：

Tk=D-+D

(10)

式中Tk为蜻蜓k的天敌驱散度；D-代表当前计算中最差蜻蜓的位置。

蜻蜓个体k飞行位置更新步长：

ΔDk+1=(eEi+uUi+bBi+sSi+tTi)+βDk

(11)

蜻蜓飞行位置更新：

Dl+1=Dl+ΔDl+1

(12)

式中e、u、b、s、t分别表示分离度、对齐度、聚集度、食物吸引度、天敌驱散度的影响系数；β代表惯性系数；l代表反复迭代计数下标；其他符号意义同前。

4 蜻蜓算法实现

4.1 算法调整

该研究对蜻蜓算法的寻优求解机制进行如下调整。

(1)引入初始种群个体优化机制。对初始种群中随机选择的某个蜻蜓个体，通过初步寻优计算得到一个可行解，优化后得到新个体替换原有蜻蜓个体，可以保证初始种群中至少有一个可行解。

(2)增加局部合理性判定机制。在蜻蜓算法中加入了合理性审查算子，该算子通过遍历单个蜻蜓的计算维度，保留飞行后合理的局部，剔除飞行后发生不合理的局部位置，以提高算法的寻优计算效率。

4.2 计算流程

适应性调整后的蜻蜓算法的计算流程包括12个步骤。

Step1：初始化计算参数，考虑梯级电站短期优化调度模型求解规模设定蜻蜓算法种群个数N=40，迭代计算次数MAXiter=200。

Step2：以梯级电站水库运行水位为决策变量，依据水位运行区域上下限ZMAX(i,t),ZMIN(i,t)，采用Xr= ZMIN(i,t)+e×(ZMAX(i,t)-ZMIN(i,t))生成初始种群，其中e为0到1之间的随机数。

Step3：随机选择一个初始蜻蜓个体，采用POA算法，基于单站优化原则，对选定蜻蜓个体进行寻优计算，确保初始种群中至少有一个蜻蜓个体为可行解。并令迭代次数iter=1，蜻蜓维度r=0。

Step4：判断蜻蜓个体Xk是否存在邻居。如果有邻居，进入Step5，否则进入Step6。

Step5：依据式(6)-(10)进行群体进化计算：分离度Sr、对齐度Ar、聚集度Cr、食物吸引度Fr、天敌驱散度Er。依据式(11)计算蜻蜓个体位置更新步长，进入Step7。

Step6：该蜻蜓没有邻居，采用Xr=e×(ZMAX(i,t)-ZMIN(i,t))进行蜻蜓个体随机飞行，进入Step7。

Step8：使蜻蜓个体计算维度加1，即r=r+1。判断是否完成蜻蜓个体全部维度的更新，如果完成全部维度的更新r=rmax，则进入Step9，否则进入Step5循环计算。

Step9：对蜻蜓个体Xk进行位置更新，Xt+1=Xt+ΔXt+1。

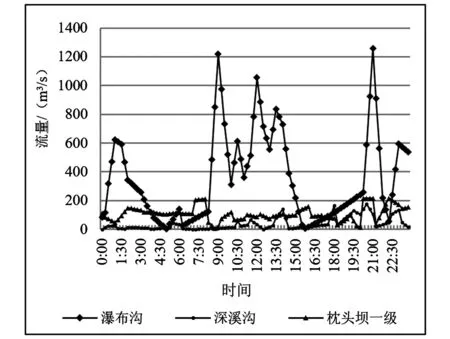
Step10：令k=k+1，进入新一个蜻蜓个体的优化计算，如果k>=N,则全部蜻蜓个体位置更新计算结束，进入Step11。若k

Step11：当前迭代次数中，找出最优蜻蜓个体，与食物位置相比较，根据是否优于食物位置目标函数值，更新食物位置，令iter=iter+1。若iter>=MAXiter，则进入Step12，否则进入Step4。

Step12：返回当前循环迭代中食物位置作为最优计算结果，计算结束。

5 实例计算

该研究选择了大渡河流域电站瀑布沟、深溪沟、枕头坝一级梯级三站为实例，其中瀑布沟水电站为季调节水库，深溪沟、枕头坝一级电站均具有日调节能力，各电站相关参数见表1[9]。

表1 大渡河下游梯级各电站主要参数

笔者选择汛期典型日进行计算求解，计算时段为15 min，设定该日三站初、末水位分别为845 m、656 m、620 m。根据流域内径流预测结果，结合上游大岗山水库的调蓄过程，该日瀑布沟水库预测入库流量过程、瀑-深、深-枕区间流量过程见图2。区间内的水流滞时分别按45 min与15 min考虑。瀑布沟前一日最后三个时段下泄流量分别为2 017.5 m3/s、2 070 m3/s、2 027.5 m3/s，深溪沟前一日最后一个时段下泄流量为1 850 m3/s。

图2 流量过程图

鉴于蜻蜓算法计算结果的不确定性，笔者选择对连续计算10次的最优值进行分析，并将蜻蜓算法计算结果与传统POA计算结果相比较(表2)，蜻蜓算法计算的梯级电站发电运行过程见图3。

表2 计算结果

(a)瀑布沟水电站运行过程

蜻蜓算法计算的梯级总发电量比POA算法计算得到的发电量略有降低，但计算时间大幅度减少。此外，梯级各电站运行过程满足电站运行爬坡率、下泄流量限制等各种约束，水库水位过程满足优化运行的一般调度规律。

6 结 语

笔者探索了新型蜻蜓智能算法在梯级水电站短期联合优化调度总的应用问题，蜻蜓算法通过模拟蜻蜓种群的“寻找食物”与“避害”等行为，在解集空间寻找优化解。但传统的蜻蜓算法注重蜻蜓个体的整体寻优，导致优化求解效率较低，甚至引起无法收敛的问题，通过对在求解计算中添加初始种群优化与局部合理性判定可以提高算法的求解效率。以大渡河流域梯级电站为实例计算验证，其结果表明：该计算结果效果略次于传统POA算法效果，但计算效率有很大提高，有效避免了“维数灾”问题，可以作为求解复杂梯级水电短期优化调度问题的方法之一。