基于风险及模式识别的电力系统支路重要性评估
赵一婕,辛 巍,范 杨,程 绳
(1.航宇救生装备有限公司武汉创新中心,湖北 武汉 430000;2.国网湖北省电力有限公司检修公司,湖北 武汉 430050)
0 引言
近年来,全球性极端自然灾害不断发生,可能导致电力系统出现从局部到大面积的停电事故[1-7],严重威胁电网的安全运行。因此,国内外学术及工程界提出采用差异化规划方法[8-9]构建核心骨干网架,以应对严重自然灾害,保障重要负荷持续供电。电网核心骨干网架[10-11]构建的关键在于对网架支路的重要性进行评估、选择与排序。文献[12]提出了一种基于小世界拓扑模型的电网脆弱性评估方法,该方法侧重于从网络拓扑建模和网络基本特征方面来寻找重要线路,但没有从电网运行特性及约束条件方面考虑线路重要性。文献[13]提出了一种基于电网生存性评估的关键线路识别方法,该方法采用平均最短电气距离反映线路的重要性,融入了电气元件的参数特征,但是很难考虑了拓扑结构变化的概率。文献[14]提出了一种电力系统脆弱性的风险评估方法,该方法兼顾了事故概率以及事故后对整个电力系统的严重后果,对支路的重要性评估具有一定的启发意义。
在电力系统风险评估领域,多风险指标的综合方法一般采用加权形式,各种加权方法的区别主要在于各指标权重的确定[15-22]。文献[23]中利用层次分析法再结合专家调查法实现指标权重的分配,该方法有很强的解释性,但操作起来复杂。文献[24]中暂态安全风险的综合指标采用了范数加权的综合方法,该方法的权重系数受主观因素影响较大。目前,对于支路安全分级问题的研究还不够深入,文献[25]中将电压安全分为5个等级,分级原则是根据风险计算指标值来人为均匀设定每一级的风险分类区间。这种分级方法简单方便,但必须依托于综合风险值的基础之上,并且主观性强。因此,需要寻找一种客观的权重确定方法和新的分级方法,该分级方法能独立于综合风险值,并且能与综合风险计算结果相一致。
本文提出了一种电力系统支路重要性排序和分级的新思路。设定事故集为单一支路退运,得到过负荷风险、低电压风险和失负荷风险,并构成三维风险向量;采用迭代自组织数据分析算法(Iterative Selforganizing Data Analysis Techniques Algorithm,即ISODATA)将三维风险向量按照数据相似度聚类,实现每条支路风险等级初步自动评定;使用主成分分析方法对三维风险指标进行分析,将其投影到主方向轴线上就可以获取能够清晰分辨不同重要性等级的一维数据,完成综合风险指标计算,对支路重要性进行排序,并将分级与排序结果进行对比,完善支路分级结果。本文从支路退运风险角度出发,提出了支路重要性评估的新方法,为核心骨干网架的构建奠定了理论基础。
1 基于退运风险自组织的支路重要性分级
1.1 支路退运风险指标
定义电力系统的支路退运风险为支路退运的概率与退运后产生的后果的乘积,即:
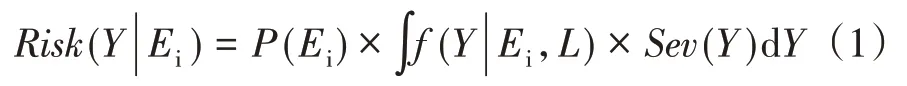
式(1)中,P(Ei)是支路i退运的概率,一般服从泊松分布;f(Y|Ei,L)是支路退运后系统处于特定运行状态的概率分布;Sev(Y)描述了在状态Y时事故的严重度。
支路退运风险考虑了单一支路退运的概率,以及该支路退运后对整个系统中其他所有元件所造成的后果,以下3种指标可以分别从不同的角度比较科学全面地评估该支路在整个系统中的重要性。
1)过负荷风险
过负荷风险是电力系统事故后,导致其他未故障支路的有功功率超过其额定值的可能性和严重程度的结合,即:

其中,过负荷严重度取决于事故后其他所有支路的潮流分布,严重度函数如式(3)所示,曲线如图1所示。
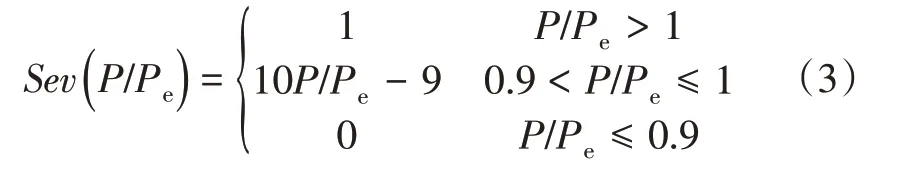
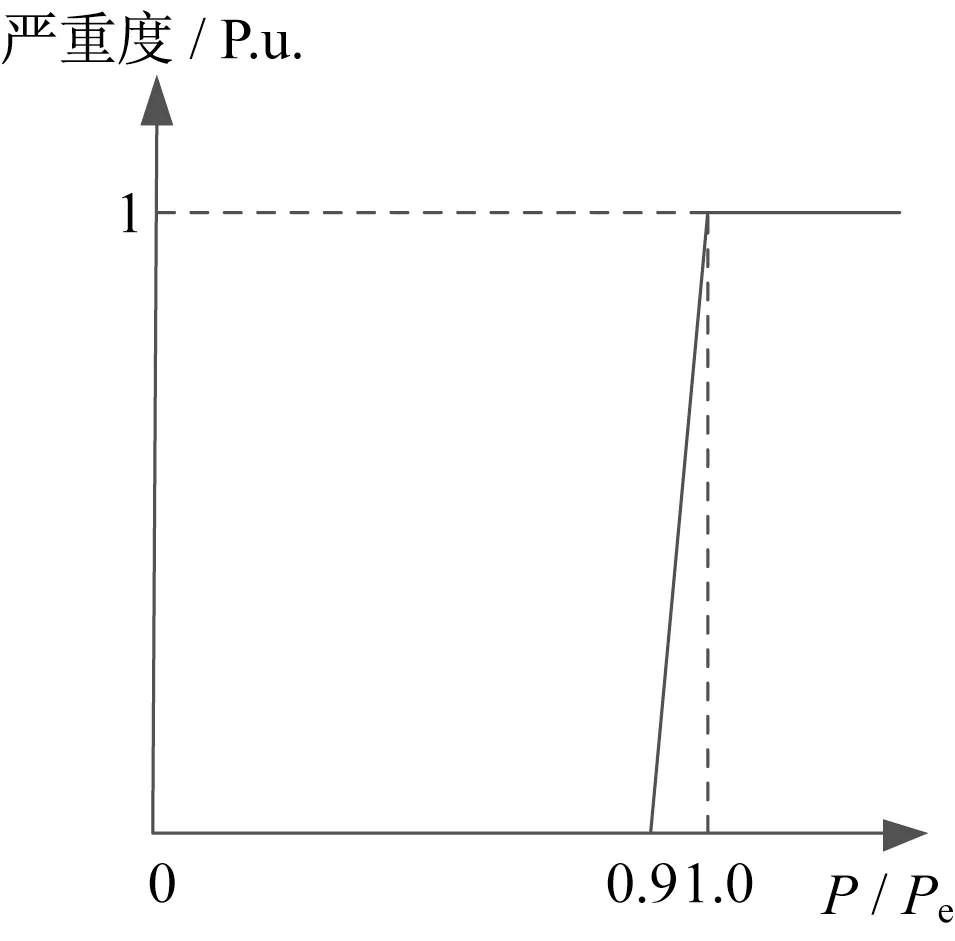
图1 过负荷严重度函数Fig.1 Severity function of overload risk
2)低电压风险
低电压风险是电力系统事故后导致系统中节点电压低于额定值的可能性和严重性的结合,即:
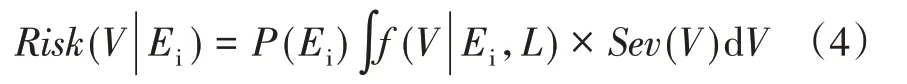
式(4)中,低电压严重度取决于事故后节点的电压,严重度函数如式(5)所示,曲线如图2所示。
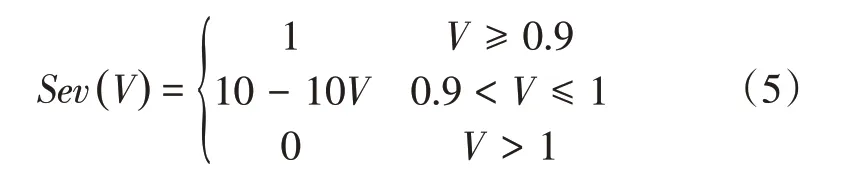

图2 低电压严重度函数Fig.2 Severity function of low voltage risk
3)失负荷风险
失负荷风险是事故后系统负荷节点失去负荷的可能性和严重程度的结合,即:
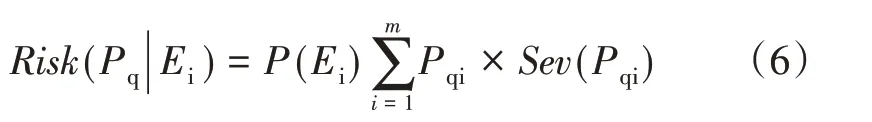
式(6)中,m为负荷节点数,Pqi为事故Ei后第i个负荷节点失去的负荷。
其中,失负荷严重度取决于失去负荷的比例,其严重度函数如式(7)所示,曲线如图3所示。
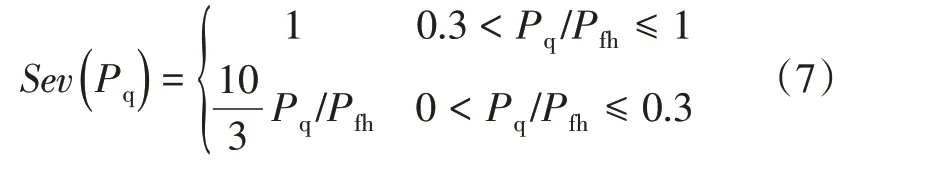

图3失负荷严重度函数Fig.3 Severity function of lostload risk
1.2 基于ISODATA聚类的支路重要性分级
ISODATA聚类,即迭代自组织数据分析算法[26-28],是一种非监督动态聚类算法的模式识别方法。ISODATA采用欧氏距离来分析数据本身的相似度,其核心思想是欧氏距离越小,相似度越大,将相似度高的数据自动聚集在一起。其基本步骤如下:
1)设置参数:待分类样本xi;预期的聚类中心数目K;初始的聚类中心数目Nc;每一聚类域中最少的样本数目θN;聚类域中样本距离分布的标准差θS;两聚类中心之间的最小距离θC;判断循环停止的迭代运算的次数IP;两聚类中心之间的距离Dij。
2)随机选取Nc个样本作为初始聚类的中心;
3)将样本xi分配到最近的聚类Sj。规则为:若Dj=min(‖ ‖xi-Cj),i=1,2,…,p,j=1,2,…,c,则将xi归到聚类Sj。
4)计算各聚类的中心:

将新的中心值定为聚类的中心Ci=Zi。
5)分裂。若当前聚类的数目少于预期的聚类数目K,则开始进行聚类分裂。
6)合并。当两个聚类的中心距离小于二者中心的最小距离θC时,两个聚类合并为一个新的聚类。若全部聚类中心之间的距离Dˉij=‖ ‖Ci-Cj<θC,就开始合并。新聚类中心为:

7)如果迭代次数达到最大迭代次数IP,或过程收敛,则迭代过程结束,否则IP=IP+1,回到步骤3。
支路重要性分级的思想即设定事故集为单一支路退运,分别计算出该退运线路的过负荷风险、低电压风险和失负荷风险,将每条支路的三个风险值表示成一个三维风险向量,采用ISODATA算法将三维风险向量按照数据相似度聚类,得到每一级的聚类中心和支路编号,实现每条支路重要性等级初步自动分级。
2 基于PCA的支路重要性排序及分级调整
2.1 主成分分析PCA
主成分分析(PCA)方法[29-32]是一种广泛应用于模式识别领域寻找多维数据主要特性的统计分析方法,其主要目的是将高维数据投影到低维空间,从多维数据中解析出主要成分,揭示多维数据有效信息,简化分析复杂问题。
PCA的主要思想是对原N维列向量使用线性变换,得到按照重要性由高到低排序的新的N列向量。在得到的新列向量中选取重要性最大的M(M<N)维子向量,作为原列向量的主成分。
记x1,…,xp为原始列向量的p个分量,设变换后列项的分量ξi,i=1,2,…,p,是原列向量子分量的线性组合,设定线性组合系数的模为1,即

这p个αi构成特征变换矩阵A。最优的正交变换A的每个分量αi使对应ξi的方差达到极值,数据将更加离散可分,相似性更低,也就代表了更多的信息。同时要求组成A的每个列向量两两正交,保证得到的新分量间两两不相关。此外,如果某维分量的方差越大,该分量就越重要,拥有更多的信息。
2.2 基于PCA的支路重要性排序及分级调整
以三维风险向量作为源数据,利用PCA方法对三维风险向量进行降维,保留源数据中的主要信息,得到所有三维风险数据的最大主方向,然后将三维风险向量投影到主方向轴线上就可以获取能够清晰分辨不同类别(即ISODATA自动分类结果)的一维数据,进而参照PCA降维结果来进行综合风险指标计算。第一主成分ξ1即为综合风险,计算公式如式(11)所示。

根据式(11)得到所有支路的综合风险,根据综合风险值进行支路重要性排序,综合风险越大,该支路故障后对整个电力系统的影响越大,因此该支路越重要。
根据支路重要性排序结果,标注空间分级投影的上下边界支路,如果相邻两重要级别支路的投影不存在交叉,则可以设定这两级的分级点为该两级的边界支路的风险平均值;如果存在允许范围内的交叉,则以重要等级高的边界支路风险为准,落在边界支路远离原点方向的投影点均自动设定为偏重要等级,按照新的两级边界支路的风险平均值作为这两级的分级点。设定分级交叉百分比为交叉支路数Njc占所有支路数Nz的百分比,如式(12)所示。

当分级交叉百分比满足ψ<10%时,可认为,采用第一主成分能够综合体现p个指标的三维空间分级信息,即分级交叉在允许范围内。
3 基于模式识别的支路重要性评估
采用ISODATA聚类算法和PCA方法,完成了支路重要性评估,流程见图4。
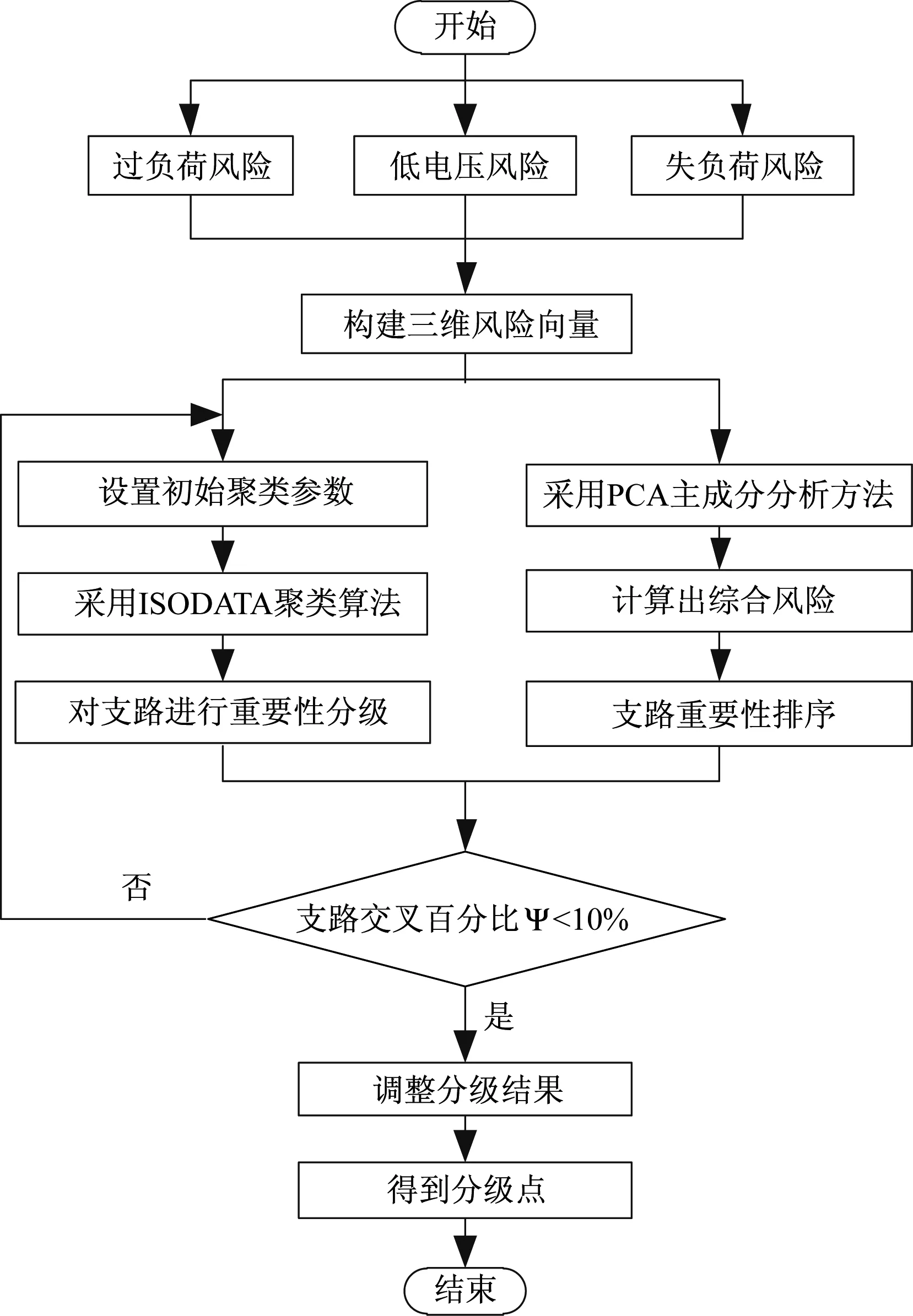
图4 基于模式识别的支路重要性评估流程图Fig.4 Assessment flowchart of branch importance based on pattern recognition
基于模式识别的电力系统支路重要性评估的具体流程分为四步:
第一步,计算所有支路的三种风险指标。设定故障为单一支路退运,分别计算出该退运支路的过负荷风险、低电压风险和失负荷风险,将该支路的3个风险值表示成一个三维风险向量。同理,可以得到系统中其他所有支路的三维风险向量。
第二步,采用ISODATA算法对支路重要性进行分级。采用迭代自组织数据分析算法将所有支路的三维风险向量按照数据相似度聚类,实现支路退运风险等级初步自分级。以聚类中心与原点欧式距离的大小来判断支路重要性等级。聚类中心距离原点越远,该级别所包含的三维风险点距离原点越远,因此这些风险点的风险就越大,其所属重要性级别就越重要。
第三步,采用PCA方法对支路重要性进行排序。采用主成分分析方法对三维风险向量进行分析,得到能够清晰分辨不同重要性级别的第一主成分,以此作为综合风险指标综合风险指标,从而完成支路重要性排序。
第四步,调整分级结果,得到分级点。将支路重要性分级与排序的结果进行比较分析,得到交叉支路,根据交叉支路百分比来判断ISODATA聚类的可行性和科学性。若满足判据,则对分级结果进行调整,找出新的分级边界支路,确定每一级的分级点;若判据不满足,则重新设定聚类参数进行支路重要性分级。
4 算例分析
4.1 算例设置
以IEEE39节点系统为例,设定负荷分配因数的波动为5%,并以此作为系统运行参数的变化。设预想事故集为系统中的每一条支路依次断开,这些支路的年开断率λy均是0.3。
根据骨干网架搜索的需要,设定支路重要性级别为三个等级,一级最为重要,二级其次,三级重要性级别最低。ISODATA算法的初始聚类中心为系统中任意三条支路的三维风险点。
4.2 支路重要性分级
经过仿真计算,得到过负荷严重度,低电压严重度和切负荷严重度,对应的风险值即为所算得的严重度与故障发生概率的乘积,三维风险向量如图5所示。采用ISODATA算法,对46条支路的三维风险进行重要性分级,分为一级、二级和三级,分别用*、+和·表示,每一类的聚类中心见表1和图5所示。
从表1可以看出,一级支路聚类中心的三个风险值均大于二级支路的聚类中心风险值,同理,二级支路的大于三级支路的聚类中心风险值。因此,重要性级别越高,其聚类中心的三个风险值比低级别的聚类中心风险值越大,该级别的所有支路相对于低级别的支路就越重要。

表1 基于ISODATA算法的支路重要性分级结果Table 1 Classification result of branch importance based on ISODATA algorithm
4.3 支路重要性排序及分级调整
采用PCA方法分析支路退运的三维风险向量,得到所有三维风险向量的第一主成分,将所有三维空间风险点向对应于第一主成分的主方向轴作投影,如图5所示,得到三维风险归一化的权重系数向量为:

图5 基于风险及模式识别的支路重要性分级图Fig.5 Grade chart of branch importance based on risk and pattern recognition
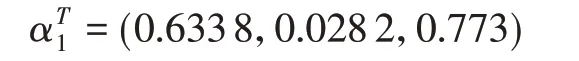
根据αT1和所有支路的三维风险向量,再结合式(11),可以计算出所有支路风险降维后的综合风险值。选取不同重要性级别的边界支路风险值列于表2所示。
对综合风险进行降序排列,得到支路重要性排序图,如图6所示。

图6 基于PCA方法的支路重要性排序及分级调整图Fig.6 Rank and grade adjustment chart of branch importance based on PCA method
结合图5和图6可以看出,一级与二级的边界支路风险落差大,两级别不存在交叉支路,因此分级点为3.877×10-4。而二级与三级的边界风险落差小一些,且存在交叉,分级交叉支路为L30(在表1中加粗标红)。这是因为ISODATA聚类将相似三维风险向量聚为一类,虽然L8和L30的综合风险很接近,但由于二级的聚类中心和L8的三维风险点均偏向轴Y(低电压风险)的正方向,根据聚类的相似性特点可知,L8为二级支路是合理的。由于Nz=1,ψ=2.2%<10%,在允许范围内。以二级分界支路为准,L8为二级支路的下分界,L11为三级支路的上分界,因此该两级别的重要性分级点为1.178×10-4,分级点如表2所示。
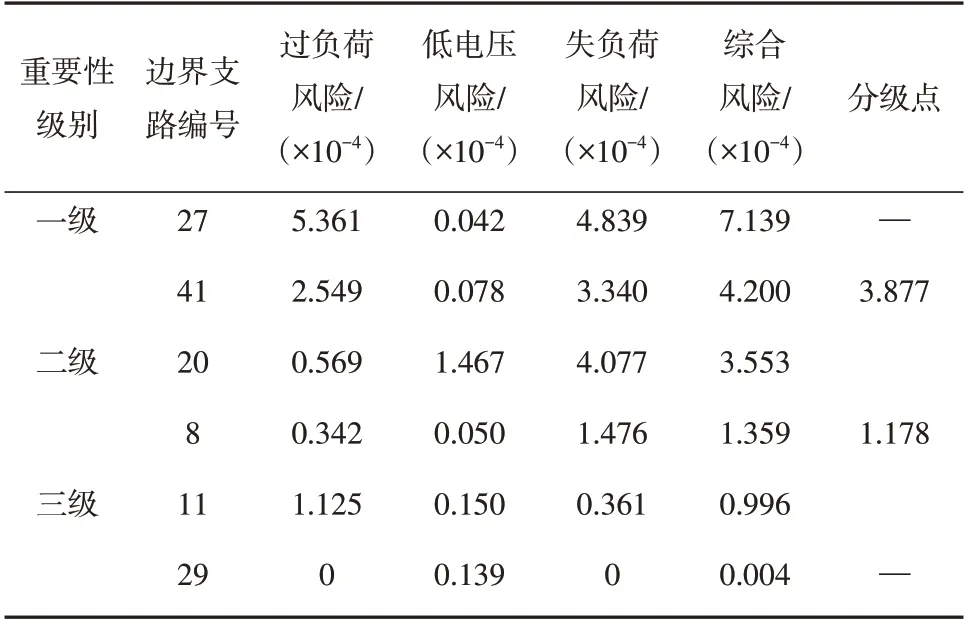
表2 边界支路风险及分级点Table 2 Risk of boundary branches and Classification point
表2选取了支路分级的上边界和下边界支路进行罗列,各级别的综合风险是依次降低的,各分指标总体上是降顺排列的,但也存在特例,例如三级支路11的过负荷风险1.125大于二级支路8的过负荷风险0.342。由于L8比L11的失负荷风险大很多,因此L8比L11的综合风险大,L8更重要是合理的。
采用聚类算法进行空间分类,以风险点距离最短为分类条件进行的风险指标值的分类,减少了人为因素的影响,更具有普适性,趋于智能分类结果。
5 结论
本文提出了电力系统支路重要性评估的新方法,采用ISODATA聚类算法,根据支路退运风险指标的相似性进行三维风险向量的初步自组织分级;采用PCA方法对电力系统的三维风险向量进行了降维分析,以所有风险向量第一主成分作为综合风险值,对所有支路的综合风险值进行排序,实现了电力系统支路重要性分级和排序。
以IEEE39节点系统为例进行仿真计算,仿真结果表明初步分级与重要性排序结果存在的交叉支路百分比ψ<10%在允许范围内,验证了这种风险分级和综合方法的有效性和可行性。该方法也适用于IEEE118节点系统,以及实际电网系统的支路重要性分级与排序。将ISODATA聚类算法与主成分分析方法相结合在电力系统支路重要性评估中的应用,为综合指标的计算以及重要性支路的选取提供了一种有效且智能的方法,从而为构建核心骨干网架提供了理论支撑。

