刚性耦合对多索股结构自振特性的影响

张卓杰，谷利雄，王东强，陈 炜，蒋 凡

(1.石家庄铁道大学 省部共建交通工程结构力学行为与系统安全国家重点实验室，河北 石家庄 050043；2.石家庄铁道大学 土木工程学院，河北 石家庄 050043；3.华南理工大学 土木与交通学院，广东 广州 510641；4.中铁桥隧技术有限公司，江苏 南京 210061)

索是桥梁工程中常用的一种构件，一般由高强度抗拉材料按照特定形式绞捻而成，现有研究常将其视为整体性良好的柔性结构。实际工程中也存在大量带刚性耦合的多索股结构，这些索股结构不具有良好的完整性，比如：平行钢绞线斜拉索内部索股除在靠近锚固端部使用索箍夹紧，其他位置独立无黏结；悬索桥的同一吊杆可由两根或四根钢丝绳组成，钢丝绳间采用刚性架连接；为了防止大型输电线舞动，一组输电线通常使用间隔棒(隔离子)进行耦合。上述结构的共同点在于组成缆索系统的索股除在特定位置进行刚性耦合外，其他位置处索股是独立的，这可能导致系统的自振特性与单根索股或完整性良好的系统振动特性均不同。

文献[1]在考察阻尼器类型对悬索桥吊杆风振的减振效果时，考虑了双吊索之间的影响。甘泉[2]借助有限元方法求解含减振架多吊索系统的自振频率，并以此识别吊索力。文献[3-4]研究了双索股系统在弹性连接和阻尼器作用下的振动模态。孔德怡等[5]分析了安装间隔棒的双分裂导线微风条件下的振动强度。

现有相关研究一般仅针对含特定数量索股系统展开，研究侧重点各不相同。工程中常通过测试索的自振频率获取索力，学者建立了多种索力-频率换算关系式[6-8]。这些研究一般假定缆索整体性良好，此类公式对于诸如钢绞线斜拉索这种含独立索股的缆索适用性未知。文献[9-11]基于实际桥梁，采用多种测量方法测试索力，考察了振动频率法对于钢绞线斜拉的适用性，但研究并没有从理论层面上进行阐述。

为了考察刚性耦合对多索股系统自振特性的影响，首先通过理论推导得到了带刚性耦合的索股系统自振方程，然后通过振动试验对计算结果进行验证，借助算例分析了索股张力不均匀性、耦合位置等参数对系统自振特性的影响，最后将相关结论应用到索股系统振动试验与钢绞线斜拉索索力测试中，实测数据再一次验证了结论的正确性。

1 振动方程

如图1所示，由n根独立锚固的索股组成的系统，各索股长均为L。索内某位置用轻质刚棒进行连接，刚棒距左、右锚固点的距离分别为l1和l2。刚棒将整个索股系统分为两个子系统〈1〉和〈2〉，分别以各子系统左端为原点建立坐标系x1o1y1，x2o2y2。对于单根索股，可将其视为柔性弦。在各子系统内，各索股振动方程为

(1)

图1 索股系统模型

(2)

式(2)可通过分离变量法求解，其解形式为

(3)

(4)

(5)

2 方程求解

式(3)为含2n个待定系数的联立方程组，其解可通过边界条件、耦合关系确定。

2.1 边界条件

根据边界条件应有

(6)

将式(3)、式(4)代入，若式(6)恒成立，则

(7)

(8)

2.2 位移连续性要求

刚结点位置处各索股的位移时刻相等，即

(9)

式中：r，s为索股号，取值范围均为1至n(若无特别说明，下同)。

式(3)、式(4)、式(7)代入式(9)可得

(10)

要想式(10)恒成立，应满足[12]

(11)

(12)

这表明经刚棒耦合，各索股振动同频，且刚结点处振动同幅。

2.3 竖向力平衡要求

某时刻系统振动位形示意见图2，在刚结点处各索股张力的竖向分力应满足平衡要求。

图2 索股系统振动位形示意

假定索股振幅微小，则有

(13)

忽略由此引起的轴力变化，根据刚节点处竖向力的平衡条件，可得

(14)

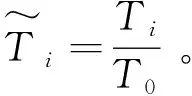
代入式(3)、式(4)，因振动同频，即式(10)消去公因式后可得节点处力的平衡条件为

(15)

3 拉索自振频率方程

式(12)的3组方程中相互独立的为2组，整理式(8)，式(12)和式(15)，可得

(16)

根据式(5)、式(11)应有

(17)

式中：p，q为子系统号。

(18)

将以上参数代入式(16)并写成矩阵形式

KX=0

(19)

式中：K为3n×3n的系数矩阵；X为3n×1的待定系数列向量。若式(19)有非零解，系数矩阵行列式为零，即

det(K)=0

(20)

根据式(20)可得带刚性耦合的双索股系统自振频率方程

(21)

对于3索股系统，仿照前述步骤可得其自由振动频率方程

以此类推，对于n索股组成的系统，在刚棒耦合作用下系统的自振频率方程为

(23)

频率方程为超越函数，可通过常规的数值方法(如二分法)求解。

4 参数分析

为研究刚性耦合对多索股系统振动特性的影响，对含多索股系统进行算例分析。选定系统单根索股的初始张力为30 kN，线密度为1.24 kg/m，索股长L为50 m，刚棒距离锚固端5 m，即L/10处。若索股间完全粘结，拉索可以看作完整性良好的柔性弦，按照弦理论可算得索股的基频fs1为1.555 Hz，且各阶频率与基频成整倍数关系。而对于仅在刚棒耦合作用下的索股系统，系统呈现的振动频率不再和基频保持良好的倍频关系。2索股系统在给定条件下的前5阶振动频率见表1。由表1可知，2索股系统在整数倍基频频率之间出现了非整数倍基频频率，比如1.11倍、2.22倍等。为描述方便，本文称这些非整数倍基频的频率为“分数倍频”，等于整数倍基频的频率称为“整数倍频”。

表1 2索股振动频率 Hz

为进一步研究刚性耦合作用下拉索的自振特性，分别对拉索的索力均匀性，刚性耦合位置进行参数分析。

4.1 索力不均匀性对自振频率的影响

由于索股独立锚固，各索股张力可能不同。选择2索股系统和5索股系统进行参数分析，其基本参数如前所述，但改变索力的不均匀度分别为5%、10%、20%，测试工况及系统索力分析见表2。索力不均匀度为5%时，各索股系统的前十阶振动频率fn及fn与fs1的比值见表3。

表2 索股力偏差分布 kN

表3 不均匀度5%时系统前十阶频率 Hz

由表3可见，此时各系统fn与fs1的比值都不再保持严格的比例关系，但从近似的关系看，系统振动频率同样呈周期性变化。2索股系统以2个频率为一个循环周期，5索股系统以5个频率为一个循环周期。在第k个循环内的首个频率与均匀性良好的拉索的第k阶振动频率fsk非常接近，而剩余阶次频率与fsk或fs(k+1)的差别较大。仿照前述做法，将这些与fsk接近的频率称为第k次整数倍频，而第k次与k+1次整数倍频之间的频率明显偏离整数倍频，称之为第k循环的分数倍频。

对于表2所示其他不均匀度的索股系统，对前20阶频率进行分析，分别计算各拉索第k次整数倍频及其分数倍频与对应阶次fsk的偏差，其百分比分布见图3。

图3 前20阶自振频率与对应阶次fsk的偏差分布

由图3可见，对于不均匀度为10%和20%的拉索同样存在整数倍频和分数倍频。对于2索股系统，整数倍频和分数倍频交替出现；对于5索股系统，1个整数倍频和4个分数倍频交替出现。由于第k次整数倍频与整体性良好的拉索的第k阶振动频率fsk偏差较小，分别计算各拉索第k次整数倍频与对应阶次fsk的偏差，见图4。

图4 不同均匀度下整数倍频与对应阶次fsk偏差

由图4可知，整数倍频与fsk的偏差呈现波动变化，偏差波动幅度与索力不均匀度呈正相关。，即使对于具有相同不均匀度的拉索，增大拉索内各股索力的不均匀程度也会增大整数倍频与对应阶次fsk的偏差。

刚棒的耦合作用可减小拉索整数倍频与对应阶次fsk的偏差。对于双索股拉索，当索力不均匀度在5%以内时，各阶主振动频率与对应阶次fsk的偏差均小于2%；当最大不均匀度达到20%时，各阶主振动频率与对应阶次fsk的偏差均小于9%，且前50阶整数倍频中80%的阶次与对应阶次fsk的偏差小于3%。

当索力不均匀度一定时，增加索股根数有助于减小偏差。比如当不均匀度为20%时，双索股拉索的前三次整数倍频与对应阶次fsk的偏差百分比分别为-3.61%、-3.31%、-2.75%，当索股增加至5根时，对于5-(5)拉索，前三次整数倍频与对应阶次fsk的偏差百分比分别减小至-2.08%、-1.90%、-1.57%。

因为整数倍频接近或等于基频的整数倍，带刚棒耦合的拉索与整体性良好的拉索具有比拟性。

4.2 耦合位置对拉索自振特性的影响

改变各拉索刚棒的位置，令其分别在L/10～L/2之间变化。索力不均匀度分别为10%和20%的拉索中刚棒位于L/10、3L/10、L/2处，各拉索前20次整数倍频与对应阶次fsk的偏差分布情况，见图5。

图5 耦合位置对整数倍频与fsk偏差的影响

由图5可知，各拉索的第k次整数倍频与对应阶次fsk的偏差呈波动变化，但总体来说，随着锚固位置增高，拉索耦合效应增强，整数倍频与对应阶次fsk的偏差显著减小。当刚棒位于拉索中央时，对于不均匀度为20%的拉索，其整数倍频与对应阶次fsk的偏差均小于2%，当不均匀度减小至10%，偏差减小至1%以内。

5 索股系统振动试验及应用

5.1 索股结构振动试验

为进一步验证上述结论的正确性，在实验室进行2索股系统振动试验。钢绞线索股两端锚固于反力架上，自由长度均为3.37 m，钢绞线质量为1.106 kg/m，索股间采用轻质刚性棒耦合。锚固端安装穿心式传感器用于测试钢绞线张拉力；在每根钢绞线索股上安装加速度传感器，同步测量耦合索股系统振动过程中的系统自振频率。

当两根索股均施加30 kN的张力时，分别测量两索股在无耦合条件和在L/10处刚性耦合条件下钢绞线的振动频率。为进一步验证理论推导的正确性，采用Ansys软件进行仿真分析。考虑到索长较短，抗弯刚度对索股振动可能产生影响，分别采用Beam188单元和Link10单元进行模拟，钢绞线抗弯刚度通过文献[13]所述方法识别确定。相关结果见表4。

表4 均匀索力条件下拉索自振频率实测值与计算值

由表4可知，当索端力相同时，两索股自振频率实测值差别非常小。由于本文未考虑钢绞线的抗弯刚度，因此与用Link10单元计算的结果一致，可验证推导的正确性。自振频率计算值略小于实测值，对比Beam188模型的计算值可知，钢绞线抗弯刚度导致自振频率略微增大。随着索股长度增加，钢绞线的弯曲刚度对于自振频率的影响将降低。当索股系统在L/10位置处耦合后，实测值表明两索股振动一致，且在整数倍频之间出现分数倍频，实测值与计算值具有较好的相符度。

为考察索力不均匀度对索股系统自振频率的影响，进一步改变索力两索股张力值，使1#索张力偏大2.5%，即张力为30.75 kN；2#索张力偏小2.5%，即张力为29.25 kN，相关测试结果与计算结果见表5。

由表5可知，当两索股索端力发生改变时，索股的自振频率将随之改变；当索股耦合后，实测值和计算值均表明，主振动频率接近无偏差系统的索股振动频率。上述结果可以验证理论推导的正确性。

表5 索力不均匀度5%时索股系统自振频率实测值与计算值

5.2 振动频率法测试钢绞线拉索索力

振动频率法是工程中测量索力经常采用的一种方法。由于钢绞线斜拉索索股间独立无粘结，拉索不具备良好的完整性，这可能影响振动频率法的测量精度。

根据前述研究可知，若在拉索上安装刚性耦合装置，可保证钢绞线索股振动同频，这是使用振动频率法测试索力所需满足的首要前提。此外，在刚棒耦合下，拉索振动存在整数倍频和分数倍频，刚性耦合可大大降低整数倍频与fsk的偏差。对于5索股拉索，当不均匀度在10%以内，可保证整数倍频与fsk的偏差小于5%。因为带刚性耦合的索股系统与整体性良好的拉索具有比拟性，使用振动频率法测试钢绞线拉索索力时，事先用刚性构件将各索股箍紧，可大大提高振动频率法的测量精度。

为此，以一座在建的三跨钢桁架拱桥为工程背景进行实桥测试。该桥使用斜拉扣挂法架设，扣索采用φ17.8低松弛钢绞线，抗拉强度为1 860 MPa。单个扣塔设置两层扣背索，每层沿横桥向设置4根钢绞线拉索(编号1#～4#)，上层扣背索单束采用20根钢绞线，下层单束采用24根钢绞线。钢绞线索股采用等值张拉法[14]进行张拉，张拉过程中在基准索和被张拉索端安装测力传感器。

扣索张拉完成时，钢绞线间独立无黏结，为增强拉索的整体性，钢绞线采用临时索箍绑扎(见图6)。同一工况下，其中的2根扣索索力目标值T0与绑扎前、绑扎后的索力实测值T，见表6。

图6 绑扎后的钢绞线拉索

由表6可知，绑扎可降低索力实测值与目标值之间的偏差。因为绑扎前索股存在独立振动的可能性，索力均匀性对测试结果产生一定影响；传感器所采集的频率实际上反映的是与之接触的索股的振动频率。绑扎后各索股振动发生耦合，减弱了个别索力偏差较大的索股对测试结果的影响。此外，从采集的频率来看，绑扎后的拉索呈现的振动频率均为整数倍频。

表6 索力理论值和绑扎前后实测值

桥梁工程中的钢绞线斜拉索一般在索两端安装索箍，与单个索箍相比，双索箍进一步增强了拉索的整体性；此外，钢绞线外套管的自重与几何约束作用可使得部分索箍发生耦合[15]，这将进一步降低索股张力不均匀问题对索力测试结果的影响。

6 结论

针对刚棒对多索股系统自振特性的影响进行理论和实测研究，可得到如下结论。

(1)刚性耦合使索股振动发生耦合，振动频率呈现周期性的变化规律，系统自振频率可分为整数倍频和分数倍频两类，整数倍频与整体性良好的拉索的自振频率具有比拟性。

(2)刚性耦合增强了索股系统的整体性，可显著降低整数倍频与整体性良好的拉索对应阶次fsk之间的偏差；减小各索股之间的索力偏差，该偏差进一步减小。刚性连接越靠近拉索中央，对增强索股系统的整体性越明显；在其他参数相同时，增加索股的根数有助于减小整数倍频与fsk的偏差。

(3)当采用振动频率法测试钢绞线拉索索力时，应采用刚性结构对索股进行紧箍。对于桥梁中的大部分钢绞线斜拉索，当索力不均匀性小于10%时，对索股进行刚性耦合后，使用整数倍频换算的索力精度可满足工程需要。