火电机组参与深度调峰对电网频率特性的影响研究
于国强,刘克天,胡尊民,汤可怡,史毅越
(1.江苏方天电力技术有限公司,江苏 南京 211102;2.南京工程学院 电力工程学院,江苏 南京 211167)
0 引言
受到负荷功率需求低、外送能力弱、电网调节能力有限等因素影响,可再生能源发电的弃风、弃光现象严重[1],[2]。为了提高新能源的消纳能力,应对负荷出现的峰谷差,火电机组深度调峰势在必行[3],[4]。
新能源接入及渗透率的提高将导致传统火电机组的关停,进而对电网的转动惯量和调频过程造成影响。文献[5]分析了风电的频率特性,给出了不同频段内风电波动对电力系统调频的影响,提出了基于分频原理的火电机组一次调频控制方法,改善了系统频率特性。文献[6]考虑了风机出力的随机性,从概率角度对风电系统进行建模,探讨了风电波动对电网频率特性的影响。文献[7]对风电的随机性给电网频率的稳定、电能品质及经济性带来的影响进行了综述。文献[8]提出了变速风电机组的频率综合控制方法,用于解决大规模风电场集中接入使电网惯性降低的问题。文献[9]提出了以火电调频为主、风电调频为辅的一次调频联合控制策略,有效规避了系统频率二次跌落的问题,提高了风电参与一次调频的安全性。文献[10]建立了简化的低惯性电力系统数学模型,从频域角度分析了新能源接入时频率特性发生的变化。文献[11]提出了风机控制器的模型,分析了控制参数及火电机组汽轮机工作点对孤岛系统中频率特性的影响。虽然新能源具备调频能力,但在实际电力系统运行中,随着新能源的接入,整个系统惯量仍呈下降趋势[12],[13]。不参与调频的新能源大量接入电网时,将不利于电网频率的稳定[14],[15]。
针对新能源接入后,火电机组参与深度调峰对频率特性的影响,本文首先采用求解微分方程的方法分析了新能源的渗透率对电网频率特性的影响;其次考虑到深度调峰对火电机组本身及系统容量的影响,将限幅环节引入简化的单机系统的数学模型中,对限幅环节进行分段线性化处理;然后给出了不同负荷扰动下频率的解析解;最后提出了额外增加系统火电机组数量的应对措施。
1 新能源及深度调峰的影响分析
1.1 新能源对频率特性的影响分析
文献[10]给出了加入新能源后简化的一次调频线性化数学模型,如图1所示。该系统考虑了调速器系统、汽轮机系统和发电机系统,为单机模型。其中:M为发电机的转动惯量;D为发电机的旋转阻尼系数;T为涡轮机的惯性时间常数;a为涡轮机特征系数,水轮机a=-2,汽轮机0<a<1;调速器以纯增益1/R简化表示;K为同步机组的发电系数,定义为发电机发电量与整个系统发电量的比值,它与新能源渗透率之和为1;ΔPL为扰动功率;Δω为发电机转速增量;ΔPm为发电机机械功率增量;Pa为发电机的加速功率;Δu为阀门开度增量;Δωref为参考频率增量。

图1 含新能源的闭环调速系统传递函数Fig.1 The transfer function of closed-loop speed regulation system including new energy
图1所示的系统中,Δωref通常为0,关于Δω与ΔPL的时域微分方程为
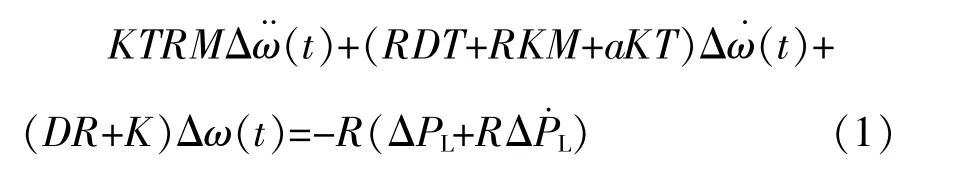
负荷扰动通常为阶跃函数,即ΔPL=ΔPε(t),其中ΔP为扰动功率,是一个常数。将ΔPL代入式(1)可知,方程右边存在对ε(t)求导的项,即冲击函数δ(t),Δω导数将突变,因此需要先求解突变后的初始条件,才能求解式(1)。式(1)两端同时对时间进行积分,有:
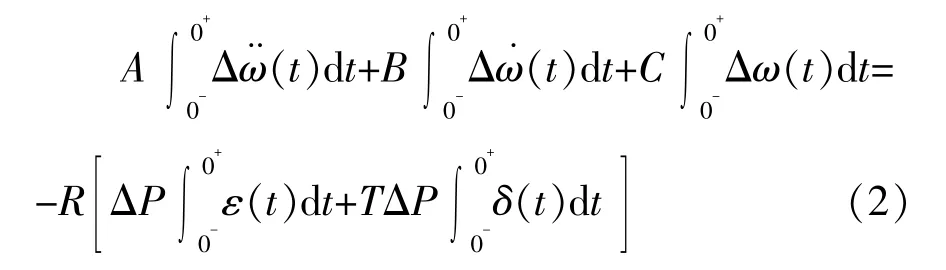
式中:A=KTRM;B=RDT+RKM+aKT;C=DR+K。
计算式(2),得到从0+时刻开始的微分方程及初始条件:

根据式(3)即可求解频率,严格上应对式(3)所有特征根进行分类讨论,但考虑到求解思路一样,且典型参数下的特征根仅为具体的一种情况,因此仅考虑特征根为两共轭虚数的情况。当特征根为两共轭系数,即B2-4AC<0时,式(1)的解为
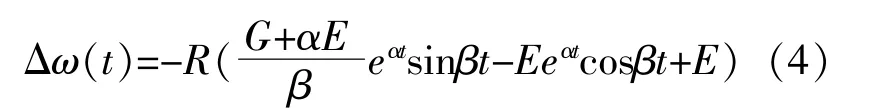
式中:G=ΔP/KRM;E=ΔP/(DR+K);α和β分别为特征根实部和虚部的绝对值。
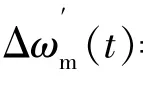

本文仅关注新能源渗透率的影响,因此将K作为变量,且忽略D,其他参数作为常量,令A=KC1,B=KC2,C=K,D1=C3/K,E=C4/K。经计算,α和β与K无关,Δωm∝(1/K)。随着新能源渗透率增加,K值减小,其到达最值的时间不变,Δωm将增大,表明新能源接入电网将恶化系统的频率特性。
本文采用文献[10]给出的典型参数,取R=5%,T=6.0,a=0.333,M=12,D=1%。令ΔP=0.1,K分别取0.7,0.8,0.9,进行时域仿真,得到频率时域曲线如图2所示。

图2 发电机频率时域曲线Fig.2 Generator frequency variation diagram
由图2可知,新能源渗透率增加时,频率稳态偏移量和动态最大偏移量增大,但几乎不影响动态最大偏移量时刻,时域仿真图像验证了理论分析的正确性。
1.2 深度调峰的影响及应对措施分析
调峰深度的定义为机组实际工况与额定工况下发出的有功功率的比值,是反映深度调峰的重要指标。参与深度调峰的机组为了运行的稳定性,功率不宜变动[16]。从火电机组本身看,常规调峰与深度调峰的区别在于调峰深度不同;从电网侧看,区别在于电网整体的调节容量发生了变化。当负荷扰动发生时,含深度调峰机组的电网调节容量变低,对系统中未参与深度调峰的机组而言,调速系统动态过程更容易到达运行极限,即限幅环节更可能动作。因此,本文引入限幅环节来描述深度调峰的影响,含限幅环节的调速系统数学模型如图3所示。其中,u0为阀门初始开度,Δu为阀门开度增量,umin和umax分别为阀门最小和最大开度,Δux为限幅环节的输入信号。

图3 含限幅环节的闭环调速系统传递函数Fig.3 The transfer function of closed-loop speed regulation system including limitng component
由图3可知,限幅环节将该系统分成3个区域,以Δux及其导数为状态变量分段列写微分方程。
①对区域1,即Δux≤umin-u0,有:
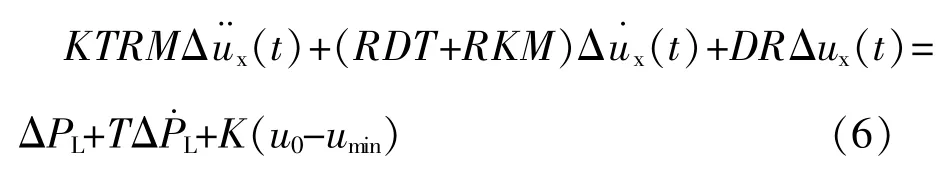
②对区域2,即umin-u0≤Δux≤umax-u0,有:
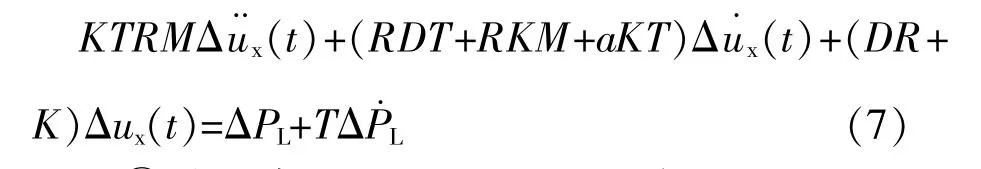
③对区域3,即Δux≥umax-u0,有:
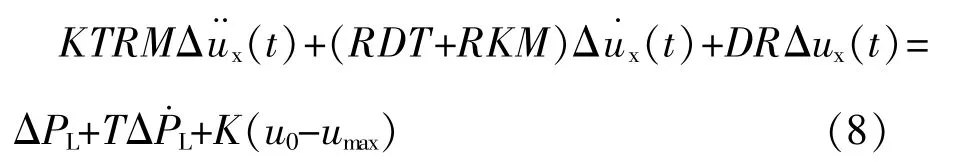
式(6)~(8)将该调速系统非线性的限幅环节进行了分段线性化处理,它们是常系数线性的微分方程,构成了整个闭环调速系统的数学模型。结合不同的初始条件可求解Δux的时域变化规律,根据Δω=-RΔux,即可研究限幅环节对频率特性的影响。
首先对求解方程的思路进行简要说明,若ΔP很小,整个动态过程限幅环节都未动作,则方程对应式(7),图3所示的系统将退化为图1所示的系统,该情况下的频率解、偏移最大时间和最大值对应式(4)和式(5)。随着ΔP值的增加,Δωm随之增大,Δux偏移最值Δum也随之增大,因此存在一个ΔPK,使得Δum=umax-u0,ΔPK即为限幅环节动作的临界扰动值。当ΔP≥ΔPK时,限幅环节一定动作,限幅环节动作时的方程对应式(8)。为求解式(8),须要求得初始条件,考虑到限幅环节图像是连续的,Δux在区域3的初始条件可根据其在区域2的解获得。之后Δux可能在区域3直接到达平衡点,也可能再次返回区域2,甚至可能出现往复振荡的现象,但求解方程的思路与最初求解区域2跨越到区域3的思路一致,而整个时域上的解由各区域的片段解连接而成。
现对区域2跨越到区域3之后的解进行求解。假定ΔP≥ΔPK,在时刻t0时,Δux=umax-u0,故当0≤t≤t0时,频率的解对应式(7);当t≥t0时,严格意义上同样应讨论式(8)的特征根情况,按照在典型参数附近取值情况考虑,即特征根为两负实数,利用式(4)求得Δux,将t0代入Δux的导数后,可得式(8)的初始条件为

结合式(8),(9)及Δω=-RΔux,可求得t≥t0时Δω的变化规律。

式中:λ1和λ2为式(8)的两个负数特征根,λ1>λ2。
C1和C2为
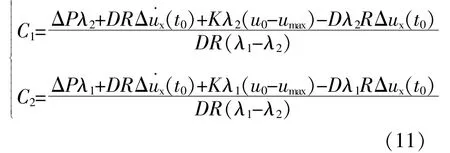
为得到限幅环节对Δωm的影响,对式(10)进行求导,Δωmax为
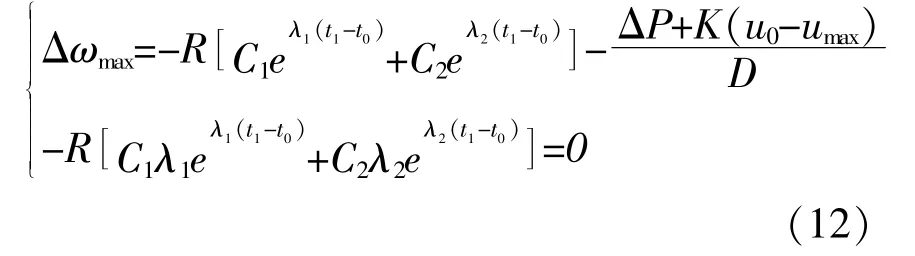
在ΔP相同情况下,比较Δωm和Δωmax,即可得出限幅环节动作对于频率偏移最大值的影响。取K=1,R=5%,T=6.0,a=0.333,M=12,D=0.01,u0=0.6,umax=1,选取不同大小的ΔP,根据式(12)和式(5)即可计算Δωm和Δωmax,结果如表1所示。

表1 不同负荷扰动下的频率最大偏移Table 1 Maximum frequency deviation under different load disturbances

续表1
由表1可知:当ΔP较小时,Δωmax和Δωm的值相同,这是因为ΔP<ΔPK,限幅环节在整个动态过程中没有动作;而当ΔP变大,ΔP≥ΔPK时,限幅环节动作,Δωmax比Δωm更小,这说明面对相同扰动,限幅环节动作时,频率动态偏移量相比无限幅环节更大,限幅环节将恶化频率动态特性。
式(7)的稳态点Δu1和式(8)的稳态点Δu2对应的频率稳态点分别为

综上所述,当电网中部分机组参与深度调峰时,由于调节容量减小,当负荷扰动发生时,非参与深度调峰的机组调速系统更容易达到限幅环节动作点,一旦限幅环节动作,其频率动态特性将恶化,稳态特性可能恶化严重。
因此,有必要采取措施增强系统的频率稳定性,其基本思路是改变系统的其他参数,使限幅环节无法动作,即Δum<umax-u0恒成立。本文提出通过增加系统中的常规火电机组数量来增强系统的频率稳定性,其优点有两个:一是增加系统的惯量,即增大了参数M,进而使Δum减小,对应不等号左边;二是系统的调节容量变大,即等价于使umax-u0变大,对应不等号右边。
为说明增大M的作用,取ΔP=0.1,M分别取8,10,12,14,16,其他参数取典型参数,通过式(5)计算得到对应的Δωm分别为-0.010 3,-0.009 9,-0.009 6,-0.009 3,-0.009 0。根据结果可看出,随着M的增大,Δum减小,这说明增加火电机组数量有利于削弱深度调峰对频率带来的负面影响。
2 算例分析
对典型的4机2节点的电网进行改造,改造后的电网如图4所示。
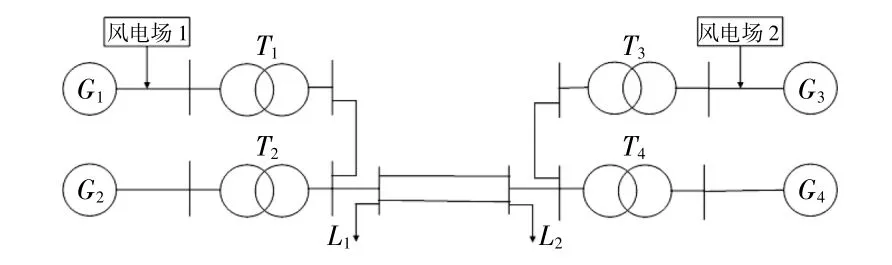
图4 改造后电网结构Fig.4 The reformed grid structure
该地区电网共有4台发电机、2个风电场源(无调频能力);2个子区域,区域1负荷为967 MW,区域2负荷为1 767 MW。风电场1和风电场2的最大功率分别为700 MW和720 MW。该系统的电压等级为220 kV,每台发电机的视在功率为900 MVA,参数R取0.05,参数H取6.5。其中,2号发电机为平衡节点,其他发电机均在额定出力,4台发电机均有调速器系统和励磁系统,该系统的惯性较大,由于风电注入量较大,可能使系统不稳定,故加入了PSS环节。
2.1 新能源对频率特性影响仿真分析
若整个系统无新能源接入,则4台发电机为负荷供电,此时风电的渗透率为0。当风电场注入功率不断增加时,1号发电机和3号发电机将被关停,整个系统有3种运行状态。本文分别仿真整个系统负荷突然增加10%时,4台发电机供电;3台发电机、1个风电场供电;2台发电机、2个风电场供电时的频率特性,如图5所示。

图5 发电机频率变化Fig.5 Generator frequency variation diagram
由图5可知:随着新能源渗透率的不断增加,在火电机组被关停的情况下,面对同样大小的负荷扰动时,频率的稳态偏移量和动态偏移量最大值都在增大;在2台发电机、2个风电场的情况下,频率出现了振荡现象,这说明新能源大量接入会导致系统频率特性恶化,抗干扰能力下降,与理论推导一致。此外,注意到最大值出现的时刻与理论推导不一致,这说明简化后的频率分析模型与实际的系统并不能完全匹配,实际的仿真说明随着新能源渗透率提升,出现动态最大偏移值的时间也在增加。
2.2 深度调峰对频率特性影响仿真分析
本文考虑3种方案:方案1,按照2台常规调峰发电机+2个风电场的情况运行;方案2,将发电机G2作为深度调峰机组,即1台常规调峰发电机+1台深度调峰机组+2个风电场;方案3,将方案2的1台常规调峰发电机改为3台相同常规调峰发电机,整个系统的负荷增加5%。3种方案下的频率曲线如图6所示。
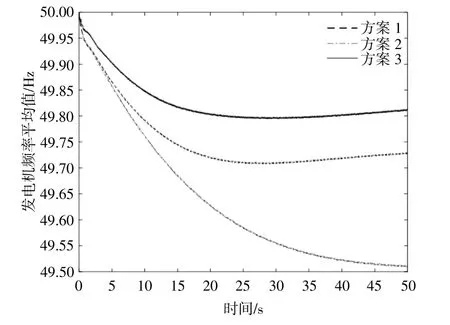
图6 发电机频率变化Fig.6 Generator frequency variation diagram
由图6中的方案1和方案2的频率曲线可知,在新能源大量接入后,部分机组直接参与深度调峰而无其他必要措施的情况下,频率特性将会恶化;由方案3的频率曲线可知,采取增加火电机组数量的措施后,频率特性恶化情况得到改善,这验证了前文关于深度调峰对频率特性的影响分析的正确性以及本文提出的应对频率恶化措施的有效性。
3 结论
①无调频能力的新能源大量接入电网,使得常规机组关停,进而影响到整个电网的惯量以及可调节容量,最终使得频率特性恶化。
②在无其他措施下,部分火电机组参与深度调峰将会使得整个系统的频率特性恶化,其原因是系统的调节容量减小了,限幅环节更有可能动作,一旦限幅环节动作,频率特性就会恶化。
③为了改善深度调峰对频率特性带来的负面影响,可采取增加火电机组数量的方法来增强频率的稳定性。

