基于机器学习的高应力软岩巷道支护抗毁能力预测

邓广哲，付英凯

（1.西安科技大学 能源学院，陕西 西安 710054；2.西安科技大学 西部矿井开采及灾害防治教育部重点实验室，陕西 西安 710054）

高应力软岩巷道支护抗毁能力始终是煤矿开采过程中核心问题，在煤矿开采时，经常出现温度逐渐升高，地应力逐渐变大或者地质逐渐发生恶化的情况，这些问题常常导致软岩巷道发生开裂、鼓包或者变形的问题[1-5]。高应力软岩巷道支护在世界范围来看，属于较为复杂的工程建设问题，对于煤矿资源开采是具有重要意义的。随着开采深度的加大，高应力软岩巷道支护问题严重突出，解决当前高应力软岩巷道支护问题，是煤炭开采过程中安全生产关注热点之一[6-8]。

目前，国内外许多学者对该问题展开了研究，余伟健等[9]针对薄煤层变形特征提出了“锚、网、索、梁”整体支护技术；王卫军等[10]提出了可接长锚杆技术对大变形巷道进行支护取得了较好的效果；黄庆享等[11]采用物理和数值模拟分析了软岩大变形巷道变形情况，提出了全断面锚杆索+梁喷浆支护；虽然上述方法取得一定的进展，但是对于复杂岩层，应用能力不足，围岩岩层基本为软岩，且巷道断面大、布置密集、强度低。随着矿山开采速度加快，深部高应力软岩巷道支护初期来压较快，巷道支护自稳能力较差，如果不加速控制很快就会出现巷道支护毁坏。而通过对软岩巷道支护效果进行预测将对围岩控制提供借鉴，刘学生等[12]采用递进预测和非递进预测方法对巷道两帮移近速度进行预测，马鑫民等[13]研发了工程类比煤巷支护智能预测系统，王宏伟等[14]采用神经网络方法对巷道变形进行了预测。但以上方法多依靠工程经验，为此，从围岩强度特性、围岩属性及流变特性等方面分析了软岩巷道支护失效机制，针对采用基于语义特征、深度学习、特征融合方法存在数据分布差异性的问题，提出了基于机器学习的高应力软岩巷道支护抗毁能力预测方法；从现有高应力软岩巷道数据中迁移知识，帮助高应力软岩巷道将来学习，并在自然环境中应用机器学习模型训练相关数据[15-20]，在这些情况下，迁移数据学习能够帮助预测研究提供全新场景，使机器学习在无大量标签数据环境下进行预测。

1 高应力软岩巷道特性分析

1.1 强度特性

因为软岩巷道存在围岩自身高应力的特点和围场低强度的性质，在此基础上，增加了软岩巷道支护措施的难度。因此开展岩石力学性质试验与分析，为高应力软岩巷道支护的稳定性提供依据。在岩石力学性质试验中，选择完整块度大的高应力软岩岩块，从岩块中取出岩心来进行物理力学性质的试验，岩石物理力学性质见表1。

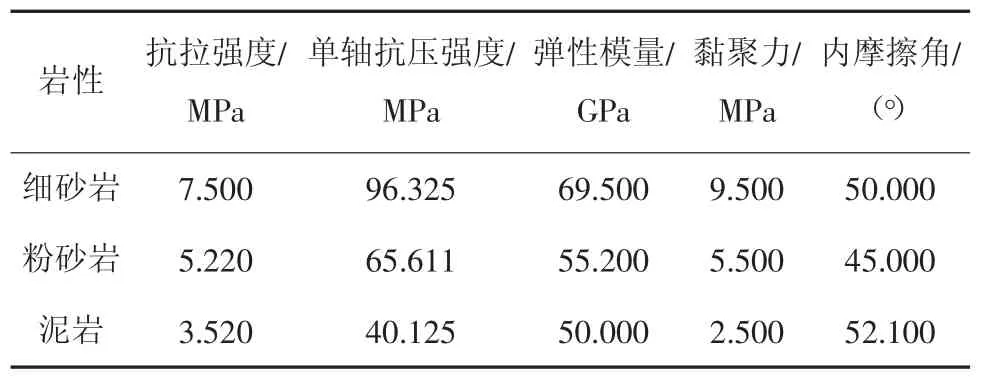
表1 岩石物理力学性质Table 1 Physical and mechanical properties of rock

由于泥岩中含有多种膨胀性黏土和矿物质，当矿泥岩与水发生混合时，泥岩承载力降低或消失，极易引发泥化、崩解的危害。因此巷道在开挖后采取封闭围岩的保护措施，尤其是对于后期失稳变形的巷道围岩，重点加强对围岩的保护。如果保护措施不当，在施工中通风、用水作业环境下，巷道围岩就会出现吸水现象，此时引发围岩体膨胀。而在失水状态下会发生岩体收缩现象，造成巷道围岩强度和完整度快速降低，加剧巷道围岩的变形和损坏[21-23]。

1.2 支护构件模型

利用FLAC3D软件建立起模拟尺寸，对模型底部位移进行约束。建模时不需要区分围岩的岩性，也不需考虑岩体的自重，只是将岩层水平简化处理，同时对围岩材料参数等效均质化处理。假定围岩三向的应力值均一样，采用六面体单元，支护构件模型如图1。

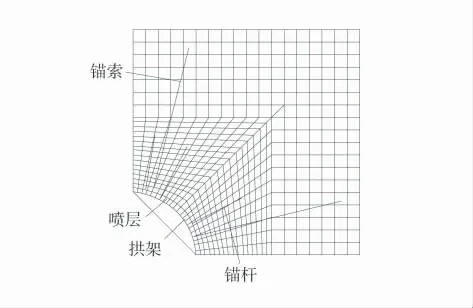
图1 支护构件模型Fig.1 Support component model

通过建立支护构件模型，设计与现场巷道条件一致计算模型，模型内等间距布置锚索、喷层、拱架、等间距布置锚杆，验证现场围岩变形破坏情况。

2 高应力软岩巷道支护阶段时间确定

软岩巷道在施工时，极易发生大变形失稳的现象，根据是由于以下特性导致的：①软岩的本质特征，当含有膨胀性矿物的泥质岩类在低应力水平的施工中，就产生了非线性、非光滑的显著塑性变形的现象；②构造、埋深和采动引起的高应力作用于软岩巷道，引起围岩的扩容变形以及围岩劣化。但不管造成软岩巷道大变形原因如何，当软岩巷道发生变形或者膨胀的变化时，各变形或膨胀区域的应变曲线是相对的。弹性区在最外围，塑性流动区在最内围。塑性硬化区和塑性软化区分布在中间层，软岩巷道变形区具体分布如图2。

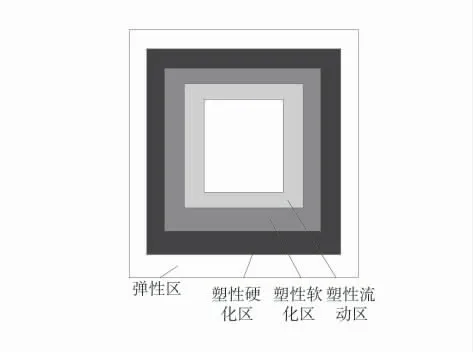
图2 软岩巷道变形区分布Fig.2 Distribution of deformation zone of rock roadway

根据图2中可知，变形速度会随着煤矿巷道开挖进展发生相应变化，其中共分为3个阶段，分别是减速变形阶段、近似线性恒速变形阶段和加速发展变形阶段，若接近最后加速发展变形阶段，巷道岩体结构就会发生巨大改变，岩体出现新的裂纹，导致其强度减弱。由于软岩巷道与硬岩巷道的本构关系，因此应采取不同支护措施。软岩巷道可以将塑性能以某种形式释放出来，因此软岩巷道支护原理可以表示为：

式中：GT为软岩周围岩层向临空区域运动的合力；Gx为弹塑性转化的工程力；Gy为软岩自撑起力；Gz为工程支护力。

在加速变形阶段，使弹塑性转化的工程力达到最大，但却大大降低了软岩自撑起力，并不满足优化准则，因此，需确定最佳支护时间。最佳支护时间是指在各个交互点所需的最佳时间，最佳支护时间如图3。

由图3可知，（G1+G0）-t表示曲线峰值点所对应的时间t1时既为最佳支护时间。通过分析可知，该点与其他曲线G0-t和G1-t交互所需支护时间相似。

图3 最佳支护时间Fig.3 Optimal support time

3 支护抗毁能力预测方案实现

机器学习是在高应力软岩巷道支护抗毁能力预测任务以性能度量衡量的性能，随着经验自我完善，通过学习归纳和总结，重新组织已有的学习结构，进而不断完善改善自身性能。通过学习进行归纳、总结，将机器学习技术应用到预测之中，可大大减少资金投入，使用机器学习方法预测高应力软岩巷道支护抗毁能力。

3.1 高应力软岩巷道支护参数求解

将高应力软岩巷道支护结构简化，简化后的模型可在软岩巷道支护上起到保护作用。若设软岩巷道支护边缘节点在检测时受到破坏，其水平方向的受力就会发生实质性变化，同时位置发生改变。高应力软岩巷道支护弹性变化过程存在如下关系：

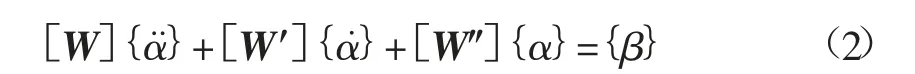
式中：［W］、［W′］、［W″］分别为高应力软岩巷道支护结构质量参数矩阵、高应力软岩巷道支护结构阻尼矩阵、高应力软岩巷道支护结构层间恢复力向量参数矩阵；α¨、α˙为高应力软岩巷道支护结构位移变化机关向量；α为高应力软岩巷道支护结构层间恢复力向量；β为外界作用力。

［W］可表示为：

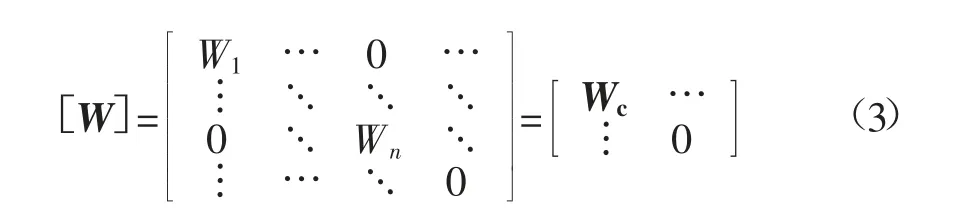
式中：Wn为第n层高应力软岩巷道支护结构的集中质量值；［Wc］为结构质量矩阵。

高应力软岩巷道支护结构仅需要考虑支护结构的外界破坏动力作用，同时忽略其余支护受力位移。采用数值积分法，获取高应力软岩巷道支护结构受到破坏的加速度和位移，由此获取高应力软岩巷道支护在破坏性外力作用下高应力软岩巷道支护受损情况。构建强破坏力作用下的高应力软岩巷道支护抗毁能力预测模型，精准分析结构抗毁性。

3.2 预测模型设计

设计强破坏力作用下高应力软岩巷道支护抗毁能力预测模型前，需对高应力软岩巷道支护加固。在中强度破坏力作用下，原始高应力软岩巷道支护加固为二次组合结构，初始原始高应力软岩巷道支护结构加固处是否有效融为一体，关键在于结合支护承载力。

在设计预测模型之前，需对支护荷载情况进行分析，在高应力软岩巷道支护体系中通常存在超高压力的现象，因此设计的预测模型需重点考虑超高压的情况，设计的高应力软岩巷道支护加固模型：

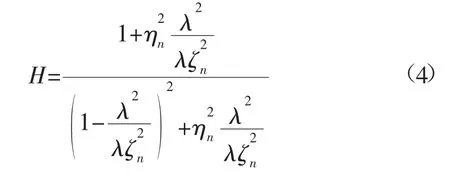
式中：H为超高压系数；ζ为引入功率谱强子；λ为描述软岩巷道支护结构属性谱参数；n为中强度破坏等级；η为高应力软岩巷道支护结构表层支护频率。

在高应力软岩巷道支护加固模型的基础上，得到的破坏生产加速度α如式（5）：

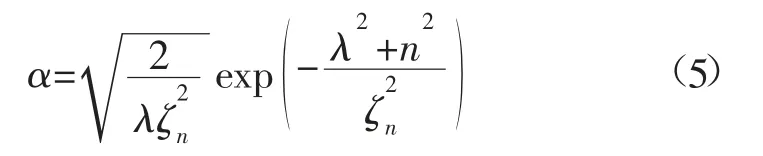
在高应力软岩巷道支护结构角位移较大处，获取最佳支护抗毁能力p预测模型：

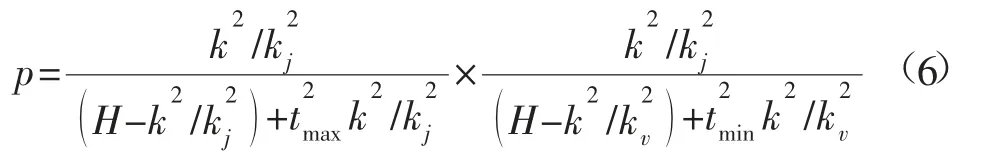
式中：kj为中强度破坏影响系数最大值；kv为中强度破坏影响系数最小值；tmax为破坏作用时间间隔最大值；tmin为破坏作用时间间隔最小值；k为破坏因子常数。

采用机器学习法对上述公式进行估算，若不考虑应力软岩巷道支护结构内部存在的扰乱因子，利用所设计的模型，分析预测高应力软岩巷道支护抗毁变化情况，最终实现中强度破坏力下高应力软岩巷道支护抗毁性的精准分析。

4 试验分析

试验采用基于机器学习的高应力软岩巷道支护抗毁能力预测方法对中强度破坏力作用下支护抗毁程度进行预测，为精准分析预测结果，以某高应力软岩巷道支护为试验对象，分析该结构分别在不同破坏强度下的抗毁程度，支护结构受损程度低，抗毁能力就越强，由此得出基于机器学习在不同破坏力下的抗毁预测结果。

不同支护方案下深部高应力软岩巷道支护位移，相关参数设置见表2。

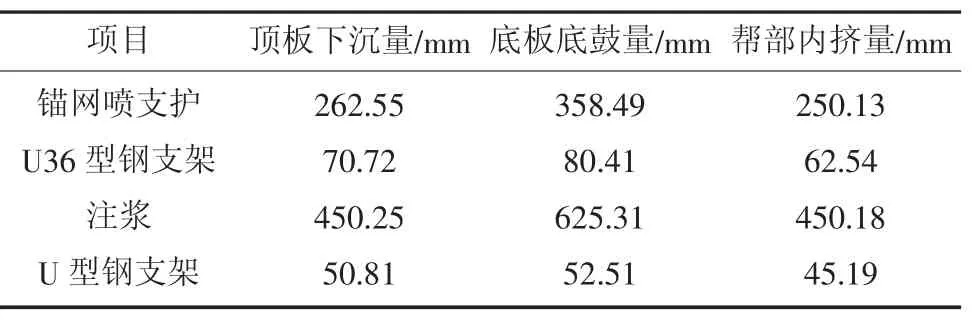
表2 相关参数设置Table 2 Related parameters setting

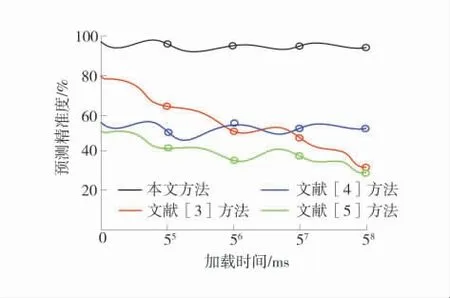
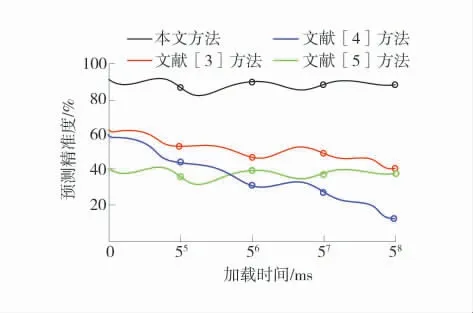
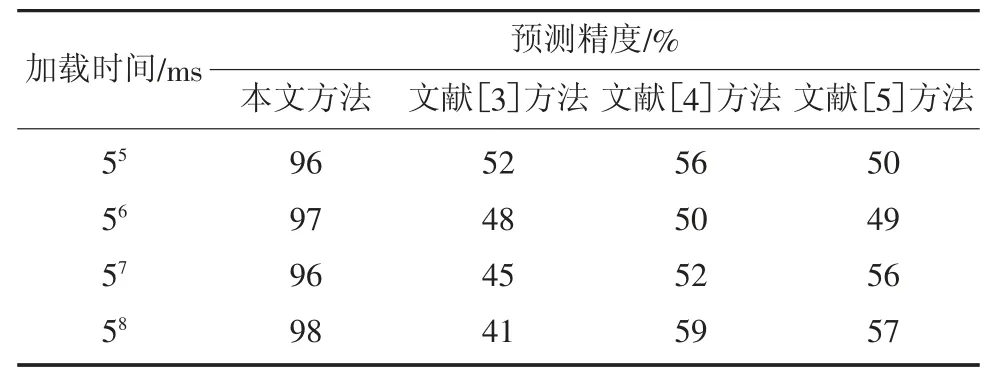
采用文献［3］、文献［4］、文献［5］方法和本文基于机器学习方法分别在M1、M2、M33种不同破坏强度（M1

4.1 M1破坏强度

在M1破坏强度下，分别将2种方法在不同加载时间下抗毁能力预测精准度进行对比分析的结果如图4。

图4 M 1破坏强度下4种方法预测精准度对比分析Fig.4 Comparative analysis of prediction accuracy of four methods under M 1 failure strength

由图4可知，当加载时间为55ms时，采用本文基于机器学习方法预测精准度为95%；而文献［3］、文献［4］、文献［5］方法预测精准度均在80%以下；随着加载时间的增加，当加载时间到达58ms时，采用本文基于机器学习方法预测精准度仍然为95%，中间呈现波动状态，但预测精准度均较高，而文献［3］、文献［4］、文献［5］方法预测精准度均呈现波动下降状态，最终均在60%以下。在M1破坏强度下，本文基于机器学习方法预测精准度较高。

4.2 M2破坏强度

在M2破坏强度下，分别将4种方法在不同加载时间下抗毁能力预测精准度进行对比分析的结果如图5。

图5 M 2破坏强度下4种方法预测精准度对比分析Fig.5 Comparative analysis of prediction accuracy of four methods under M 2 failure strength

由图5可知，采用本文基于机器学习方法预测，在加载时间为55ms时，预测精准度达到最高为94%；而利用文献［3］、文献［4］、文献［5］方法预测精准度均在65%以下。在加载时间为58ms时，本文基于机器学习方法预测精准度达到93%；而文献［3］、文献［4］、文献［5］方法预测精准度均波动下降。在M2破坏强度下，基于机器学习方法预测精准度同样较高。

4.3 M3破坏强度

在M3破坏强度下，分别将4种方法在不同加载时间下抗毁能力预测精准度进行对比分析的结果见表3。

表3 M 3破坏强度下4种方法预测精准度对比分析Table 3 Comparative analysis of prediction accuracy of four methods under M 3 failure strength

由表3可知，在不同加载时间下，使用机器学习方法在加载时间为58ms时，预测精准度达到最高为98%。而文献［3］、文献［4］、文献［5］方法在加载时间为58ms时，预测精准度最高分别为41%、59%和57%。在M3破坏强度下，本文基于机器学习方法预测精准度最高。

综上所述：在M1、M2、M33种破坏强度下，本文基于机器学习方法预测精准度均较高，其原因是本文方法在进行高应力软岩巷道支护抗毁时，巷道在开挖后采取封闭围岩的保护措施，尤其是对于后期失稳变形的巷道围岩，加强了对围岩的保护，在一定程度上节约了高应力软岩巷道支护抗毁的时间，有利于准确性的提高。

5 结 语

1）基于围岩强度特性、围岩属性及流变特性结合语义特征、深度学习、特征融合方法的思想提出了基于机器学习的高应力软岩巷道支护抗毁能力预测方法。

2）通过对比现有方法，抗毁能力预测结果与标准分析结果高度一致，且分析耗时较短，是1种有效的抗毁性分析方法。也证明了基于机器学习抗毁能力预测方法的抗干扰能力，为使用更多源项目进行训练提供了帮助。

3）高应力软岩巷道支护抗毁能力预测具有巨大应用价值，已经成为热门研究方向。由于所研究的预测方法并没有在实际科研环境中得到验证，因此，提出的基于机器学习的高应力软岩巷道支护抗毁能力预测已经很好解决了传统方法存在的数据分布差异性问题，但仍然存在一些不足需要继续优化。