重磁三维数据的模糊聚类联合快速反演

陈 强 叶险峰

（湘潭大学 土木工程与力学学院，湖南 湘潭 411105）

反演具有多解性，单一的反演方法很难反演出准确且清晰的地下模型，Vozoff 和Jupp（1975）[1]首次提出联合反演的概念，通过联合反演来耦合不同的物性信息。在此之后联合反演经过不断的发展，Gallardo 和Meju（2003、2004）[2-3]基于不同的物性参数具有同一地质结构的特性，提出了交叉梯度联合反演方法。在Bezdek（1974）[4]提出的模糊c-均值聚类算法的基础上，研究者们提出了模糊c-均值（FCM）聚类联合反演算法，后来Sun和Li（2015，2016）[5-6]又做出了一些改进，加入了先验地质物性信息，随后Sun 和Li（2016）[7]又提出了模糊c-回归（FCRM）聚类方法。Sun 和Li 在FCRM 聚类反演中使用高斯牛顿法解方程组，计算效率低，所以本文采用共轭梯度法实现FCRM 聚类反演。共轭梯度法的概念是Hestenes[8]与Stiefel[9]于1950 年首次提出的，由于收敛速度快、内存需求小，在地球物理反演中被广泛采用[10]。近年来，预条件共轭梯度法[11]和重加权共轭梯度法[12]也被广泛应用于反演中。

本文在模型目标函数的构建中采用了光滑约束，使用有限差分法计算模型加权矩阵，所以，在求解大型线性方程组的计算中，核函数和大型稀疏矩阵的存储与计算是一个不容忽视的问题。本文在涉及核函数矩阵的运算中采用了矩阵分解算法[13]，用三元组的形式表示大型二维稀疏矩阵。除此之外，本文在编程时用OpenMP 指令实现CPU 多核环境下的多线程计算，用于提高计算效率。

1 反演理论

重磁反演的基础是正演基本原理，本文使用的是一般直立六面体的正演计算公式[14]。

1.1 光滑约束

1.2 模糊c-回归聚类联合反演

联合反演可以有效的耦合多种物性信息，降低反演多解性。模糊聚类联合反演的目标函数如下：预期的线性聚类的距离，引导反演结果的线性聚类靠近预期的线性聚类，达到预期的地质分化效果。

1.3 重加权共轭梯度法

1.4 核函数矩阵的分解运算

1.5 大型稀疏矩阵的优化存储与运算

2 模型试验

2.1 简单模型

加入所述的约束条件后，反演结果如图1（c）（g）所示，根据它们可以看出传统约束反演的结果虽然显示出了中心直立长方体的位置，但是它的边界是发散的，模型和围岩的边界模糊不清。相比于磁力反演的结果，重力反演的结果很明显地下沉了，这是由于假设的地下空间的底层围岩仍有剩余密度，这就相当于存在一个拥有小剩余密度的模型，深度分辨率较差的重力反演的结果就出现了下沉的情况。

图1（d）（h）是模糊c-回归聚类联合反演得到的地下空间的密度分布图和磁化强度分布图，相比于单独反演的结果，联合反演加强了两种反演结果的共同部分，削弱了它们之间的差异部分，在图中呈现出的现象就是直立长方体所在的位置的密度值和磁化强度值更为密集，且高于围岩。而密度模型中底层的物性聚类是传统的约束反演得到的密度模型的向下发散导致，在底层位置，传统约束反演得到的密度模型和磁化强度模型在底层位置的物性产生了线性关系，这被模糊c-回归聚类联合反演误识别为模型间物性的线性关系，所以使密度模型的下沉部分加强了。

图1

2.2 复杂模型

图2（a）（b）是根据湖南省有色地质勘查研究院提供的坪宝-黄沙坪铅锌银多金属矿某处的地下剖面建模建立的复杂剖面模型。为了进行三维的反演试验，对该剖面模型进行了理想化的假设：XZ 剖面模型在Y 方向进行复制，获得多层完全相同的XZ 剖面模型。为了减少数据量，减少三维的反演试验的时间，我们在Y 方向只设置了5 层。

图2（c）（g）是传统约束反演的结果，图2（d）（h）是模糊c-回归聚类联合反演得到的结果，可以看出联合反演加强了密度模型和磁化强度模型之间共同的部分，削弱了它们之间差异的部分，改善了磁化强度模型的物性分布。虽然三维反演的多解性问题仍然严重，约束条件远远少于未知条件，但是总体来说，FCRM 聚类联合反演方法相比于传统约束反演方法是有所改进的。

图2

3 结论

针对重、磁反演问题的趋肤现象，本文采用了深度加权函数抵消核函数随深度几何衰减的影响；针对重、磁反演的多解性，本文采用了光滑约束、正定约束等多种约束；针对大型线性方程组的计算难度问题，本文对核函数矩阵进行矩阵分解计算，采用三元组实现大型稀疏矩阵的存储和计算，采用基于PRP 公式的重加权共轭梯度最优化方法，同时采用OpenMP 并行计算技术实现CPU 多线程加速，最后，采用模糊c-回归聚类算法实现重、磁数据的联合反演，并先后采用简单直立长方体模型和复杂模型进行验证，得出以下结论：

3.1 矩阵分解方法和三元组数组的引入改善了大型二维数组的存储内存大和计算时间长的问题，特别是在对两个二维数组间的计算中，这种改善尤为明显，达到了减少算法运行时间的目的；

3.2 光滑约束、正定约束等方法的引入改善了重、磁物性反演的多解性问题，深度约束和重加权反演方法很好的解决了反演的趋肤效应；

3.3 根据直立长方体模型和复杂模型的试验，对比重、磁单独反演和联合反演的结果，重、磁数据的联合反演加强了两种物性数据中一致的特征，同时又对差异的部分进行了互补和改善，联合反演得到的结果相比单独反演的结果更加真实准确。

附录A

糊聚类联合反演的目标函数如下：

为了使目标函数在线性聚类上最小化，我们求出（A-1）式对线性聚类参数vk1的导数，然后令导数方程等于0，求解得到线性聚类参数（斜率）的计算公式：

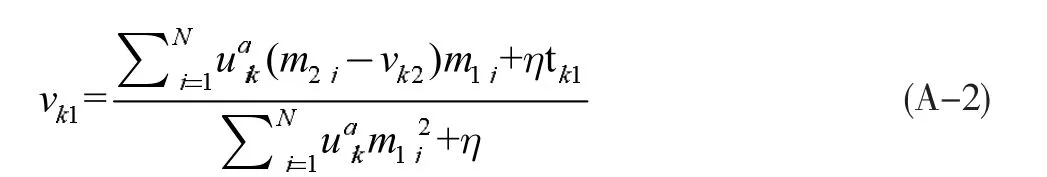
同理，线性聚类参数vk2（截距）的计算公式如下：

求出（A-1）式对隶属度函数ujk的导数，然后令导数方程等于0，求解得到隶属度函数ujk的计算公式：