星载干涉成像高度计双频基线定标方法

陆翔 张庆君 王爱明 刘杰 刘磊 韩晓磊 何德华 温中凯,3

(1 中国空间技术研究院遥感卫星总体部,北京 100094)(2 北京空间飞行器总体设计部,北京 100094)(3 南京航空航天大学 航天学院,南京 211106)

以“陆地水文及海面地形探测”(SWOT)任务为代表的新一代星载Ka频段干涉成像高度计,采用近天底角干涉合成孔径雷达测高技术,在数百千米刈幅宽度内实现海面高度厘米级的测量精度[1]。高时间分辨率(1～3天)、空间分辨率(1～10 km)及测高精度(≤5 cm)下的海面高度数据产品,能极大推动海洋物理学研究从中尺度海洋现象向亚中尺度海洋现象转变,满足亚中尺度海洋现象全周期高效精准观测,填补海洋不同尺度能量级联和物质循环链路研究的空白[2]。

干涉成像高度计厘米级的高程测量标准,严格限制了整个系统的设计指标精度和稳定性要求。由于多种原因(环境、结构状态、器件性能)共同作用,仪器位置、结构、电特性、工作性能等均会对干涉成像高度计的基线和干涉系统产生影响,从而降低干涉成像高度计在轨观测指标精度,因此必须利用适合的定标/校准技术保障整个测高系统的指标性能。干涉成像高度计的基线状态直接影响其高程测量精度,以SWOT任务为例,在距离向35 km 处,1/10000°(0.36″)基线滚动倾角误差将导致约6 cm 的海面高度误差;0.1 mm的基线长度形变会在刈幅远端造成约4 cm的海面高度畸变。因此,对干涉基线状态的在轨标定极为重要。目前,对于干涉成像高度计基线定标方法已有相关研究,在单一干涉测高频段下,文献[3]中理论分析了SWOT 基于外部参考数据的经验交叉定标方法估计干涉基线滚动倾角与长度误差,利用干涉成像高度计自交叉区域和其与传统星下点高度计(“贾森”、海洋二号卫星装载)、海上定标场等互交叉区域,仿真分析经验基线交叉定标估计方法的效果。文献[4]中基于交叉区域的海面高度数据,对干涉成像高度计基线定标进行了理论分析,在不考虑其他误差的前提下,利用交叉定标的方式仿真验证了角秒量级的基线滚动倾角标定精度。基于原位外部参考数据的干涉基线标定方法,如基于“全球导航系统”(GNSS)浮标阵列、水下滑翔机、机载激光、高分辨率海洋模式数据及海上定标场等数据,十分依赖参考数据的准确性,海面与大气环境的变化、数据的时间去相干等多种因素均会对基线状态的估计精度造成影响,较难满足实际高精度指标要求,且具体性能还需要在轨进行实际验证。文献[5]中利用天宫二号干涉成像高度计试验载荷在垂直地表入射的拓展试验中获取星下点干涉回波的相位数据,根据几何关系对干涉基线滚动倾角进行反演,修正指向偏差后的反演结果与平台测量的滚动角变化趋势一致,均小于0.005°(18″)。文献[6]中设计增加星下点发射信号,利用双侧回波信号的干涉相位信息与基线滚动倾角之间的几何关系,根据仿真模拟的海面干涉相位,理论估计了干涉基线滚动倾角偏差,基线滚动倾角的标定精度达到0.03″。海面处于不断运动状态,依据干涉雷达测量体制,星下点处干涉图像的相干性较低,基于星下点干涉相位的基线估计方法在精度等方面也会受到一定影响,同时也需要在轨进行验证。

本文针对星载干涉成像高度计定标方法,提出双频基线海面高度同程测量模式,利用重叠观测区域有效降低介质、海面运动、空间环境、时间去相干、雷达系统等引起的海面高度误差,获取高精度海面高度数据,满足干涉成像高度计基线参数的精确估计需求,可有效提高海面高度数据产品质量。

1 干涉成像高度计测高原理

双天线干涉成像高度计测高原理与工作模式[7]如图1[8]和图2所示。图2中:h为待测点P 海面高程,见式(1);水平分置于卫星两侧的天线1和天线2之间的基线长度为B;H 为天线1几何中心到海面的垂直距离;θ为雷达下视角;r1和r2分别为2副天线到观测目标点的斜距,斜距差Δr＝r2－r1;Oe为地心;Re为地球平均半径;α 为基线滚动倾角。

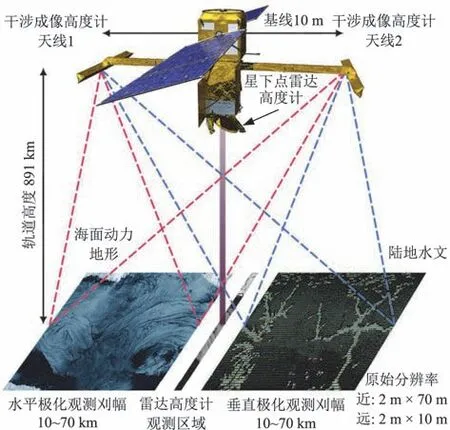
图1 SWOT 任务示意Fig.1 Conceptual illustration of SWOT mission

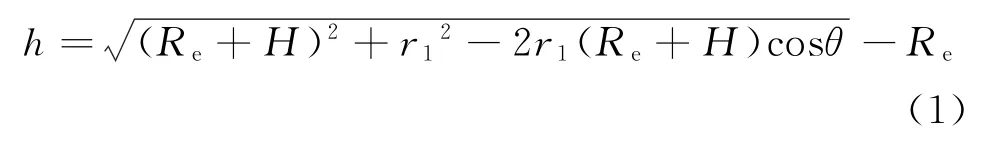
干涉相位为

式中:k 为电磁波波数;λ 为雷达波长。

在海面高度测量过程中,距离星下点x 处(交轨向刈幅宽度)干涉基线滚动倾角变化δα 与长度变化δB 引起的测高误差δh 分别为[9]

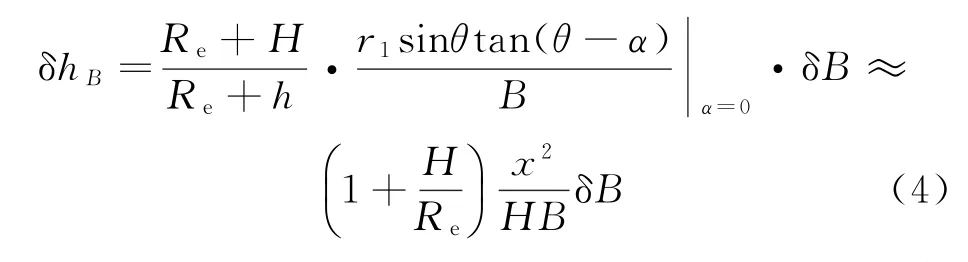
在幅宽范围内,基线滚动倾角误差造成的测高误差随幅宽的增大呈近线性增长趋势,基线形变误差产生2次阶的高度误差影响,基线状态的变化对整幅图像精度造成局部的倾斜。同时,基线滚动倾角也会造成系统相位偏差,从而引入额外的高程误差。因此,干涉基线状态的确定精度,直接影响了最终海面高度数据产品的性能。

2 双频基线定标方法

在单频干涉成像高度计基线参数标定估计过程中,基于海面高度参考数据与测高误差简化理论模型的经验基线定标方法,不仅依赖重叠区域中参考高度数据的准确性,同时对观测数据与参考数据之间的时效性要求较高,并且相位噪声及系统相位漂移、干/湿对流层、海况条件等引起的海面测高偏差也在一定程度上降低了基线参数标定估计的精度,使后期数据处理过程中对微米、毫角秒量级的基线参数指标要求的估计压力成倍增加。因此,为了缓解数据处理中基线参数估计的难度,尽可能提供较高精度的干涉基线状态参数初值,本文提出一种高时效、高精度的干涉成像高度计双频基线定标方法。该方法是在原有单一频段干涉成像高度计系统的基础上,增加另外一个频段的天线与馈源系统,实现干涉成像高度计双频组合重叠观测模式,如图3 和图4所示。图4 中以天线1 和天线2 观测示意为例,h 是重叠观测区域中参考目标点P 的先验高度信息,B 是天线1和天线2之间的标称基线长度,H1和H2是地固坐标系下天线1和天线2几何中心垂直地表的距离,θ1和θ2是天线1和天线2的雷达下视角,r1和r2是天线1和天线2几何中心距参考目标点P 的斜距,Re1和Re2是天线1和天线2星下点对应的地球半径,γ 是天线1和天线2波束中心的入射角夹角。在重叠观测区域中,进行同时、同程观测的2个频段干涉测高系统降低了由于大气传输路径造成的干涉相位误差,能有效提升在轨干涉相位精度;同时,结合高度计回波和数据、高精度基线在轨测量[10]数据,保证高精度在轨基线标定;考虑到同时观测的效果,2组基线状态基本相同,可有效避免由于时间间隔导致的空间环境与基线在轨状态参数变化引起的基线参数定标精度下降问题。

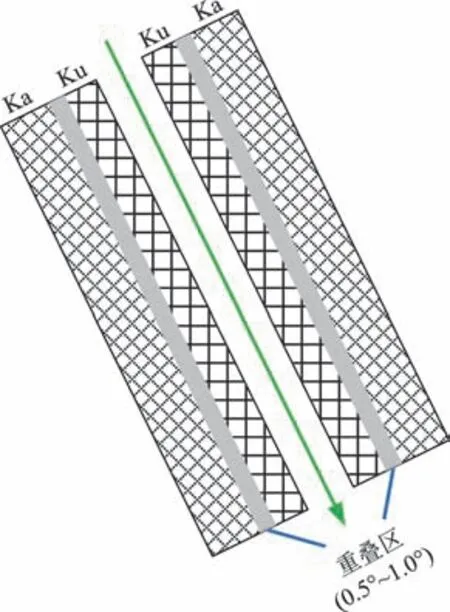
图3 双频基线标定区域示意Fig.3 Schematic diagram of dual-frequency baseline calibration area

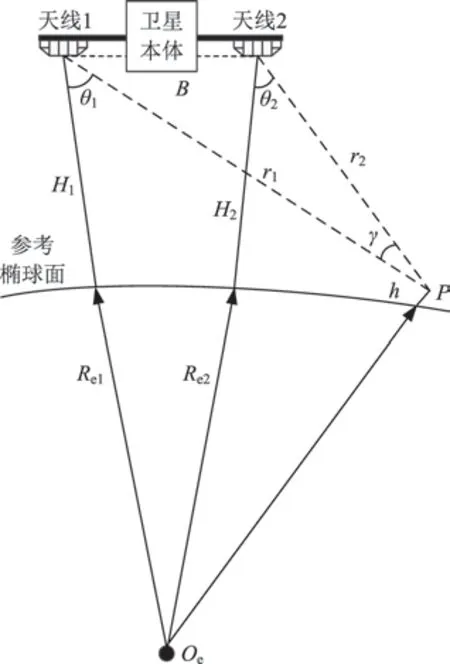
图4 双频基线标定方法示意Fig.4 Illustration of dual-frequency baseline calibration method

干涉相位测量精度除了取决于卫星和有效载荷干涉测量精度,还会受到电离层、对流层等大气传输路径引起的附加相位影响。Ka频段受到电离层影响小,Ku频段受对流层(云雨)影响小,利用双频同时重叠观测模式,能进一步降低电离层和对流层对干涉相位的影响,提升干涉相位测量精度。同时,较好反演处理后的准确海面高度信息可以提升基线长度、基线滚动倾角等参数估计精度,有效校正基线在轨随机偏差带来的海面高程不确定性。双频基线定标方法结合星载高精度基线测量装置、雷达系统信息、干涉成像高度计相关数据及地面基线估计算法,实现基于重叠区域海面高度值的在轨基线高精度测定能力,极大降低干涉基线滚动倾角、长度变化导致测高性能的退化。

2.1 基线定标方法总体流程

本文将Ka频段单频干涉成像高度计扩展成Ku和Ka双频干涉成像测高体制,方法具体流程如图5所示。其中,η 为预设相位偏差门限。

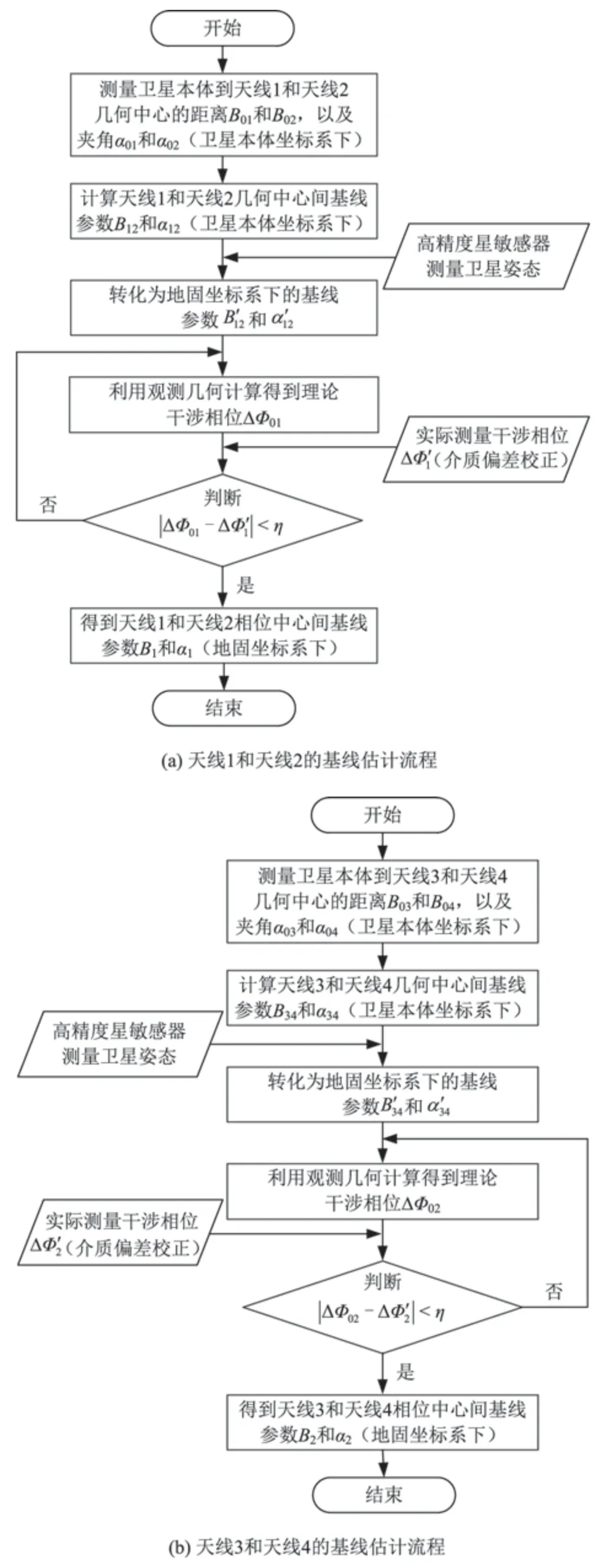
图5 双频基线标定方法流程Fig.5 Flow of dual-frequency baseline calibration method

干涉成像高度计由2组4副天线组成。其中:天线1和天线2相对于卫星本体对称安装形成基线B1,覆盖高度计视场外侧,用于收发Ka频段射频信号;天线3和天线4相对于卫星本体对称安装形成基线B2,覆盖视场内侧,用于收发Ku频段射频信号。Ka和Ku频段信号覆盖视场形成一定角度波束重叠区(一般为0.5°～1.0°)。利用在轨基线测量、高精度星敏感器等辅助设备,开展星地联合基线估计,实现亚毫米、亚角秒的高精度基线估计精度。

2.2 定标方法原理与实现

如图6所示(以天线1和天线2为例),建立卫星本体坐标系。其中:O 为卫星质心,X 轴为卫星飞行方向,Z 轴为指向地心方向,Y 轴与X 轴、Z 轴成右手定则,XOY 平面为飞行方向与展开基线形成的平面。

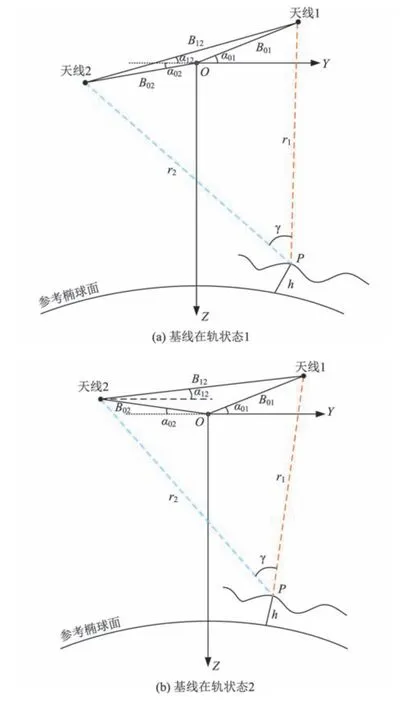
图6 双频基线定标方法测量几何示意Fig.6 Schematic diagram of measurement geometry by dual-frequency baseline calibration method

首先,计算Ka频段的基线长度B1和基线滚动倾角α1(地固坐标系),具体步骤如下。

(1)利用在轨高精度基线测量设备(激光和视觉相机等),测量卫星本体质心到天线1和天线2几何中心的距离B01和B02,卫星本体质心到天线1和天线2几何中心连线与卫星本体坐标系的XOY 平面的夹角α01和α02。

(2)计算卫星本体坐标系下天线1几何中心与天线2几何中心的基线长度B12和基线滚动倾角α12。

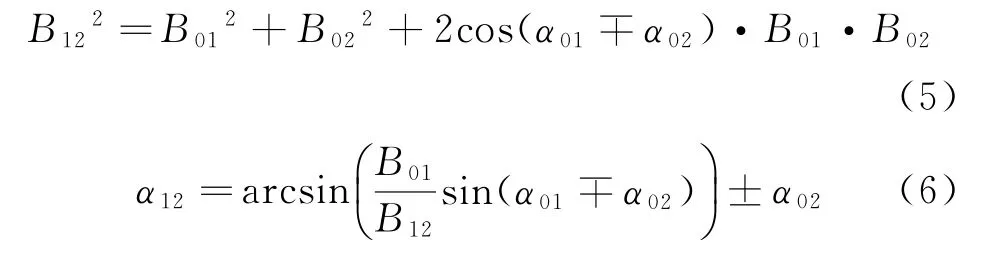
(3)将天线1与天线2几何中心在卫星本体坐标系下的基线长度B12和基线滚动倾角α12转换为在地固坐标系下的基线长度和基线滚动倾角

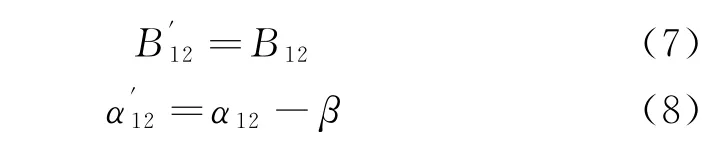
式中:β 为卫星相对于地固坐标系下大地水准面的姿态转角,通过在轨星敏感器测量得到。

(4)利用参考目标点的观测几何,计算得到参考目标点的理论干涉相位Δφ01。根据在Ka频段和Ku频段重叠区域中参考目标点的先验高度信息h,地固坐标系下天线1和天线2几何中心距离地面的高度H1和H2,以及天线1和天线2的雷达下视角θ1和θ2,计算天线1 和天线2 几何中心的斜距r1和r2。

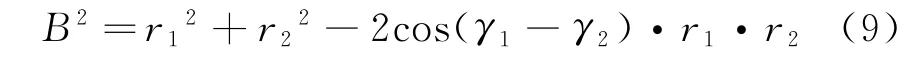
式中:γ1和γ2分别为天线1和天线2波束中心的入射角,见式(10)。

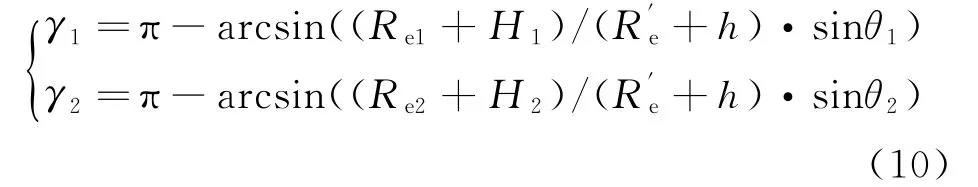
参考目标的理论干涉相位为

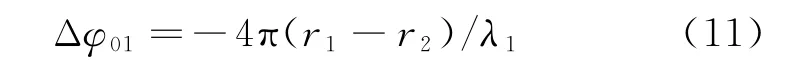
式中:λ1为天线1 或天线2 发射Ka频段信号的波长。

(5)通过干涉成像高度计测量,雷达回波中获取参考目标点的测量干涉相位Δφ1,进一步去除电离层和对流层的影响,提升测量干涉相位的准确性

式中:Δφion 为电离层相位偏差;Δφtrop为对流层相位偏差。

(7)调整天线1与天线2几何中心在地固坐标系下的基线长度和基线滚动倾角。

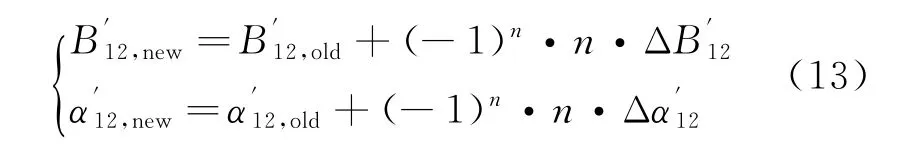
然后,按照同样的方法计算Ku频段(即天线3和天线4)的基线长度B2和基线滚动倾角α2(地固坐标系)。

最后,变更共同覆盖范围内的参考目标,重复计算多组基线长度B1,B2和基线滚动倾角α1,α2,求取平均值作为基线长度和基线滚动倾角的终值。

3 仿真验证

3.1 基于海面高度数据的双频同基线重叠观测效果仿真

基于SWOT-simulator的功率密度谱分析的方法,仿真20 km 重叠区域海面高度相关数据,在仅考虑基线滚动倾角、基线长度、干涉系统随机噪声、湿对流层延迟对海面高度的影响作用下,通过数据拟合的方法验证采用单频与双频模式下干涉基线状态标定的性能影响,仿真参数如表1所示。

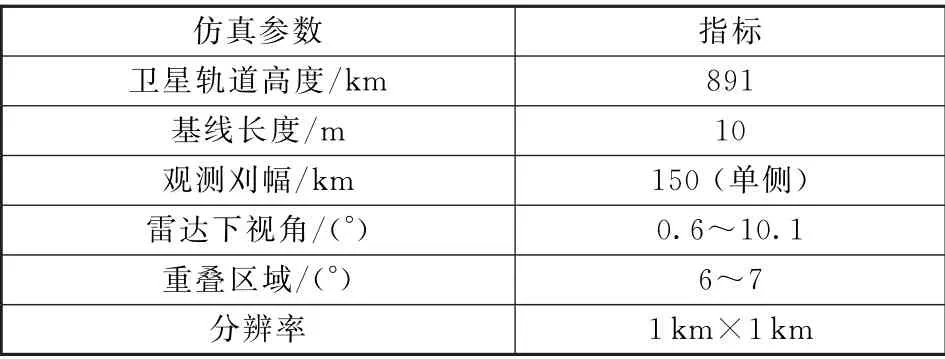
表1 仿真参数Table 1 Simulation parameters

仿真结果如图7所示。采用双频基线进行的标定,基线滚动倾角估计偏差的均方根从0.80″降低至0.19″,基线长度估计偏差均方根从0.63 mm 降低至0.15 mm。同时,海面高度误差从最大0.8 m降低至0.25 m,如图8所示。

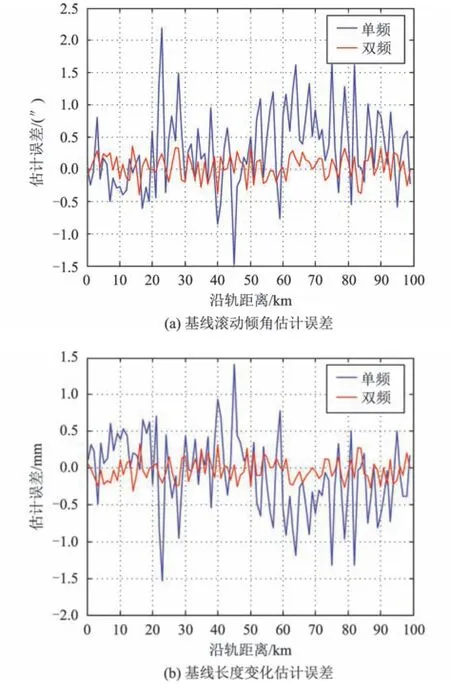
图7 单频与双频模式下基线滚动倾角与基线长度的估计误差Fig.7 Roll angle and baseline length estimation errors with single frequency&dual-frequency

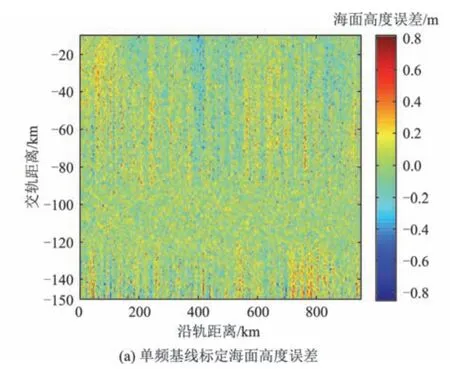
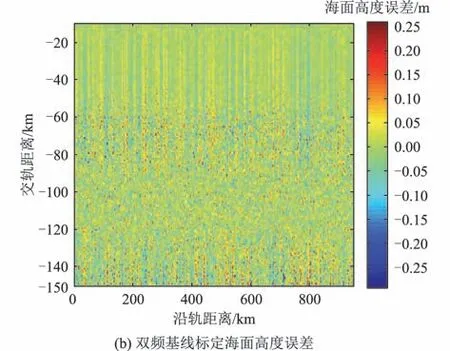
图8 单频与双频模式下基线估计误差引起的海面高程变化Fig.8 Sea surface height for baseline estimation errors with single frequency&dual-frequency

3.2 基于星载基线测量装置的基线状态估计仿真

假设卫星轨道高度为945 km,基线长度20 m,重叠刈幅的下视角范围为7°～8°,星载基线测量装置可以实现基线滚动倾角1″、基线长度1 mm 的测量精度,根据上文所述的双频基线定标方法,在重叠观测区域中,利用参考点的海面高度数据与基线在轨测量数据,仿真计算基线参数定标的结果,如图9所示。对比仅使用星载基线测量装置和采用本文方法,基线滚动倾角估计偏差的均方根由1.01″降低至0.29″,基线长度估计误差均方根由0.95 mm 降低至0.17 mm。

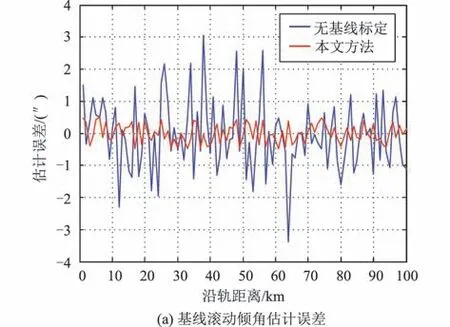
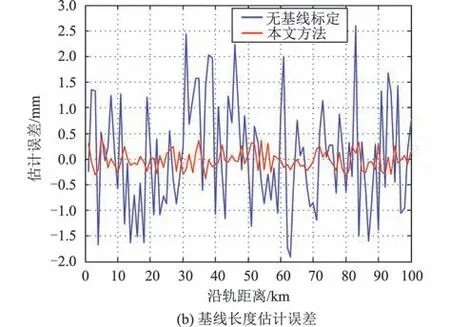
图9 双频模式下基线滚动倾角和基线长度的估计误差Fig.9 Baseline roll angle and length estimation errors with dual-frequency

星载干涉成像高度计可采用双频进行同程观测,利用参考点、基线测量系统、高度计回波等数据实现基线参数的标定,降低了传输介质、相位噪声等影响,基线长度与基线滚动倾角的标定精度提高至亚毫米和亚角秒(4～5倍),保证了海面高度测量精度。

4 结束语

星载干涉成像高度计的基线会因空间环境变化、卫星的姿态、轨道控制等多种因素导致状态的改变,从而引起卫星海面高度测量精度的下降。本文提出应用双频基线进行干涉成像高度计基线参数标定的方法,采用双频同基线重叠观测可以有效降低介质及系统偏差等误差影响,较好地获取高精度海面高程基准。同时,利用星上实时测量的基线状态信息作为基线估计初值,使用多个准确系统参数联合基线估计,能实现更为精确的基线参数标定,提升整个测高系统的定标效果。亚角秒的基线滚动倾角与亚毫米的基线长度估计精度,将有效降低基线状态漂移对干涉成像海面高度测量精度的影响。随着星载干涉成像高度计卫星在轨部署及专属海洋定标场的建立,能极大推动干涉成像体制高度计在轨定标与性能校验方法的研究与验证,完善并加深对宽幅体制高度计指标设计、误差预算、数据精度分析等多方面内容的理解。