基于改进差分进化算法的密封舱结构优化设计
施丽铭 姚远明 赵启林 马森 邓宇华 陈浩森
(1 北京空间飞行器总体设计部,北京 100094)
(2 南京工业大学 机械与动力工程学院,南京 211800)
(3 北京理工大学 先进结构技术研究院,北京 100081)
差分进化[1](Differential Evolution,DE)算法是以达尔文生物进化论“优胜劣汰”的思想为准则,模拟自然界生物进化的群智能优化设计方法,主要包括初始种群的生成、基于差分形式的变异、基于概率选择的交叉和基于“优胜劣汰”思想的选择4个步骤。由于其原理简单、控制参数少,故在不同的领域均有广泛的应用,如卫星调度[2]、无线传感器网络定位[3]、应急物资配置调度[4]等。虽然DE 算法有很多优点,但也存在易陷入局部收敛的缺点,主要原因是:变异操作是DE算法进化个体的关键,原理是对不同个体之间的向量差进行加权计算,以此实现种群中每个个体的扰动[5],但随着迭代的进行,种群之间各个体开始朝一处或多处聚集,个体之间的差异性迅速减少,导致个体之间的向量差减小,以至于个体无法进化,进而导致算法陷入局部收敛,即“早熟”。因此,改进DE算法的“早熟”缺陷将会对提升算法的性能有着重要的意义。
对于“早熟”的缺陷,不少学者对此进行了改进,方法大致包含以下几方面:自适应调整控制参数[6-7](变异率F 和交叉率CR)、变异策略的改进[8-9]以及混合算法的使用[10-11]。例如文献[6]借鉴自然界生物繁衍的“S 型曲线”,提出基于S 型变异率的差分进化算法(SDE),改进的算法在一定程度上解决了变异算子的参数设置问题,但其采用的DE/rand/1变异策略[1]并不利于中后期局部精细搜索;文献[8]提出基于双变异策略协调工作的自适应差分进化(DSDE)算法,该算法采用双变异策略来共同产生变异个体,改善了单一策略带来的不利影响,但每一步进化过程都采用双变异策略变异,增加了计算时间,同时其后期采用较小的变异率也不利于算法跳出局部最优解;文献[10]提出一种基于共轭梯度法的反馈差分进化混合算法,能够根据种群自身的搜索环境来选择变异方式,同时采用共轭梯度法确定局部搜索方向,提高了最优值的精度,加快了收敛速度,但共轭梯度法对于多峰、高维函数的计算量太大。
为进一步提高DE 算法的计算精度和收敛性能,改善“早熟”的缺陷,本文提出一种基于自适应变异率的双策略差分进化(AD-DE)算法。该算法借鉴了SDE算法的变异率规律,变异率随着迭代次数增大而增大,同时采用双重变异策略DE/rand/1和DE/rand*best[1],并采用函数T 根据当前迭代次数动态的选择变异策略,使得算法在探索和开采之间取得动态的平衡。后将改进的AD-DE 算法应用于某型密封舱的结构优化中,取得了较理想的结果,为密封舱的设计提供了参考。
1 DE算法的改进
为缓解DE 算法易陷入局部收敛的缺陷,本文主要从变异率和变异策略两个方面出发对DE 算法进行改进,提出一种具有自适应变异率和双变异策略的DE算法,命名为基于自适应变异率的双策略差分进化(AD-DE)算法,期望改善算法的计算精度和收敛性能。
1.1 变异率的改进
变异率控制着差分的步长,影响着种群多样性。一般在进化初期,由于初始种群为随机生成,因此个体分布均匀,种群多样性大;但随着迭代的进行,由于贪婪选择的择优选取,导致个体慢慢的聚集于一处或多处,因此在迭代后期种群多样性下降,算法丧失进化动力。为提高算法在迭代后期的进化动力,本文提出自适应变异率Fa,其公式为
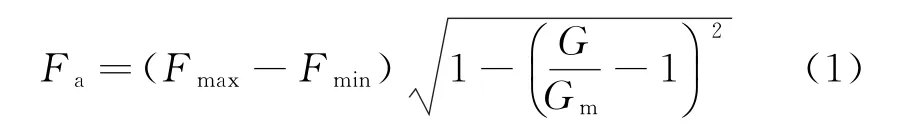
式中:Gm为最大迭代次数,G 为当前迭代次数,Fmax、Fmin分别为变异率上、下限。
图1为Fa的变化曲线,改进后的变异率随着迭代的进行单调递增:在进化初期,Fa较小,有利于维持初始种群的种群多样性,保护初始种群中的优良个体和基因;在进化后期,Fa值较大,有利于增大种群多样性,为后期进化提供动力,增加算法跳出局部最优解的可能。

图1 变异率曲线Fig.1 Mutation rate curve
1.2 变异策略的改进
对于DE 算法,不同的变异策略会对算法性能造成不一样的影响。受多变异策略的启发,本文将全局变异策略和局部变异策略进行综合。全局变异策略能在解空间内广泛地搜寻最优解,快速锁定较优的开采区间;局部变异策略主要集中在个别较好的个体附近,具有很强的开采能力。在进化前期,采用搜索范围广的全局变异策略来产生变异个体,帮助算法快速确定较优的开采区间;在进化后期种群个体较为集中,我们采用改进的局部变异策略,来更好的对较优个体进行深度开采,同时也能避免后期采用较大变异率带来的不易收敛的弊端。
本文采用DE/rand/1为全局变异策略,变异策略公式为

式中:qG,i 代表第G 次进化的第i个变异个体(i=1,2,…,Np),Np为种群规模;pG,n为被执行差分的个体,pG,m、pG,k 为执行差分的个体;n,m,k 代表个体的随机选择索引,n,m,k ∈{1,2,…,Np},且i≠n≠m≠k;Fa为自适应变异率,即差分向量的缩放因子。
采用自主开发的DE/rand*best为局部变异策略,DE/rand*best变异策略公式为

式中:a 为在(0,1)之间的随机数,旨在减弱最优个体的影响,防止陷入局部最优;pG,best代表第G 代最优个体,旨在增加搜索目的性;pG,x、pG,y、pG,z为执行差分的个体;x,y,z 代表个体的随机选择索引,x,y,z ∈{1,2,…,Np},且i≠x≠y≠z。
对于上述两种变异策略的选择,构造如下的T函数为变异策略的选择函数,原因在于:所构造的T 函数值介于0~1之间,便于使用概率映射的方式来选择变异策略;当G=时,代入式(4),T 为0.5,便于划分迭代的前、后期。
函数T 公式为

函数T 曲线图像如图2所示,由图2可知,在迭代初期,T 近乎为1,在迭代后期,T 近乎为0。故设置一随机数Q,Q ∈[0,1]。在进化初期,Q 很大概率上会小于T,此时选取DE/rand/1作为变异策略;在进化后期,Q 很大概率上会大于T,此时选取DE/rand*best作为变异策略,变异策略选择公式如式(5)所示。

图2 函数曲线图Fig.2 Function graph

这样,在进化前期有更大概率选取全局变异策略,在进化后期有更大的概率选取局部变异策略。
1.3 AD-DE算法描述
AD-DE算法步骤如下:
(1)设置种群个数Np,最大迭代次数Gm,变异率上、下限Fmax、Fmin,交叉率CR,初始化种群;
(2)利用式(4)计算当前进化代数G 下的T,利用式(5)来选择变异策略,当随机数Q 小于T,选择DE/rand/1为当前G 下的变异策略,否则选择DE/rand*best为变异策略;
(3)利用式(1)计算当前进化代数G 下的变异率Fa,按步骤(2)选择的变异策略进行变异操作;
(4)检查变异个体是否超出边界,若超出边界则将其舍弃并重新随机生成;
(5)使用二项交叉模式进行交叉操作,交叉率为CR,生成试验种群;
(6)计算目标种群和试验种群个体的适应度值并比较大小,采用贪婪选择的模式进行选择;
(7)判断是否达到最大迭代数或者满足迭代终止条件,若满足,停止,输出最优解;若不满足,则返回步骤(2)。
2 仿真校验及分析
2.1 试验设计
为全面体现本文AD-DE 算法的综合性能,试验选用如下8个测试函数[12,13]对算法的性能进行验证,分别为:Sphere函数、Rosen Brock函数、Rastrigin函数、Griewank 函数、Ackley 函数、Quartic with noise函数、Schaffer函数、Shekel函数。这些函数涵盖了单峰、高峰、多维、不规则的优化问题。
本文对比试验所选用的算法如下。
(1)参考文献[14],变异率F 为0.8,变异策略为DE/rand/1的DE算法,记为DE1;
(2)变异率F 为0.8,变异策略为DE/best/1的DE算法,记为DE2;
(3)变异率在[0.4,0.95]范围内呈现“S”型变化,变异策略为DE/rand/1 的SDE 算法[6],记为DE3;
(4)使F 和CR呈负相关的自适应差分进化算法[7],记为DE4(为新型的改进差分进化算法);
(5)本文所提出的基于自适应变异率的双策略差分进化算法AD-DE算法,变异率在[0.2,0.95]范围内变化,变异策略为DE/rand/1、DE/rand*best,记为AD-DE。
优化设计过程中,个体数Np=10D,D 表示搜索空间的维度,初始种群在搜索空间内随机分布。将各对比算法、不同测试函数和不同维度D 条件下的平均值和标准差计算结果汇总于表1中,并将最优计算结果进行加粗处理。其中函数f1~f6为高维函数,故分别设置D=10,20,30 时的情况做对比;f7、f8为二维函数,故D=2。对于每种测试函数的每种维度情况,分别进行50次独立的优化设计计算,记录这50次优化计算的最优值,并计算50次最优值的平均值和标准差。为直观给出AD-DE 算法效果,绘制各测试函数的迭代曲线图,如图3 所示,图3中(a)~(h)为D=30(对于测试函数f7、f8,D=2)时各测试函数典型迭代曲线,图3中横坐标为迭代次数,纵坐标为最优值取对数。
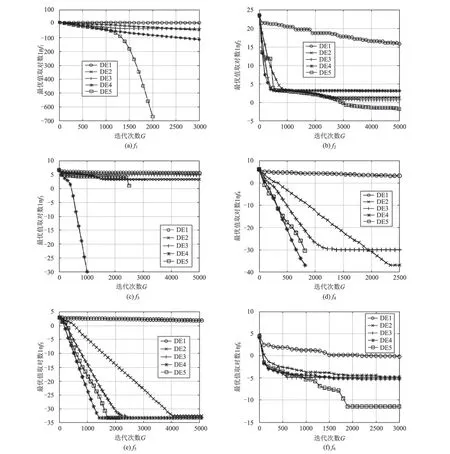

图3 不同算法迭代趋势图Fig.3 Different algorithm iteration trends

表1 不同算法寻优结果的平均值和标准差Table 1 Average and standard deviation of optimization results of different algorithms

续 表
2.2 试验结果及分析
本文从以下方面对实验结果进行评价:①通过平均值和标准差来反映各个优化设计方法的优劣。当平均值越接近理论最优值时,结果最优;若平均值相同,则标准差越小,即算法越稳定,计算结果越优。②迭代趋势图,以曲线的形式显示每种算法每种测试函数的寻优历程。
由表1可知,在高维函数f1~f6中:低维时,除f2外,与其它算法相比AD-DE 算法均取得了更优解,其中f3、f4、f5均精准的找到了理论最优值;对于f2,AD-DE 算法也仅次于DE3。中维时,除f3外,相比其它算法AD-DE 算法求解的结果更接近理论最优解且标准差也更小;高维时,除f2外,AD-DE算法在f1、f3、f4、f5处均找到了全局最优解,f6虽然未找到全局最优解,但相比其它算法其平均值更加接近最优解,标准差也更小。在二维函数f7~f8中:对于函数f7,DE4和AD-DE 均找到了全局最优解且标准差均为0;对于函数f8,虽然DE3、DE4、AD-DE均找到了全局最优解,但AD-DE的标准差更小,说明对于该函数AD-DE 算法更加稳定。由此可知,AD-DE算法不仅在低维时能取得较好的结果,随着维数的提升,算法依旧能保持较好的性能,且AD-DE 算法对不同函数的适应能力要显著高于对比算法。
由图3可知,在相同的迭代次数下,AD-DE算法分别在测试函数f1、f3、f4、f5、f7、f8中第2066、2560、952、2185、255、26代处均找到了全局最优解,表明AD-DE算法的收敛速度高于对比算法,平均提速50%以上。同时也证明了AD-DE算法跳出局部最优解的能力最强,并且能快速的找到全局最优解。
综上,AD-DE算法明显地强于对比算法,它能在探索和开采之间取得动态的平衡,在保证后期种群多样性的同时,可提高求解的精度和收敛速度。
3 AD-DE算法在密封舱结构优化中的应用
结构的优化问题,就是在满足约束条件的情况下,使得结构质量越低,成本最小化的问题。对某密封舱进行建模分析,可知其属于多变量的复杂优化问题,因而采用求解精度和收敛性能更好的AD-DE算法对其进行优化。
3.1 密封舱模型及工况介绍
某型密封舱模型如图4所示,为加筋球壳结构。选取特定工况,并将各荷载乘上相应的荷载安全系数(见表2)。密封舱上各设备分布情况为:设备一安放在地板框;设备二安放在帽檐板连接框;其它设备质量均布在各加强筋上;平台对接框为固接。
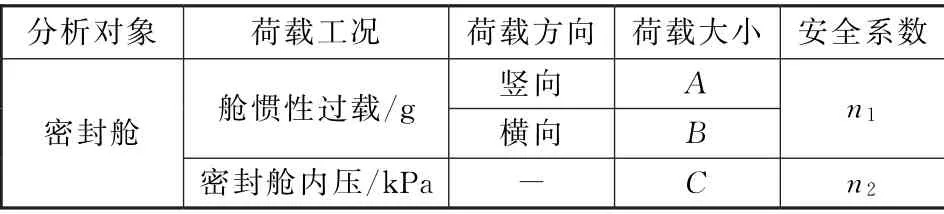
表2 荷载Table 2 Loads

图4 密封舱结构Fig.4 Structure of capsule
3.2 应用ANSYS和Matlab软件协同优化密封舱
优化以密封舱质量最低为目标函数,以强度和几何尺寸为约束条件,以蒙皮壁厚和各肋条截面尺寸为设计变量。利用Matlab 软件进行AD-DE 算法的编写,利用ANSYS-APDL 软件对密封舱进行参数化建模。以 Matlab 软件作为主控程序,ANSYS软件作为求解器进行有限元分析,整个优化设置在Matlab中全部完成[15]。
具体的操作步骤如下。
(1)设置AD-DE算法基本参数,种群规模Np=20、最大进化代数Gm=55、变异率上、下限Fmax=0.95、Fmin=0.2,交叉率CR=0.9;
(2)在设计变量约束区间内,随机生成设计变量所得值,初始化种群;
(3)将初始的设计变量值存入Input.txt 文件中;
(4)应用ANSYS软件读取Input.txt文件,以读取的值作为设计参数进行结构分析;
(5)提取分析后的结构最大应力S 作为约束条件,提取密封舱的结构质量W 作为目标函数;
(6)将约束条件和目标函数存入Output.txt文件中;
(7)Matlab 软件读取Output.txt文件,计算Np个个体的适应度函数值,并从中获取最佳个体和其适应度值;
(8)判断是否满足终止条件,若满足则停止优化,输出最优设计变量和目标函数值,若不满足则运行步骤(9)和(10);
(9)执行1.3节中的步骤(2)~步骤(6);
(10)获得G+1代设计变量值,循环本节的步骤(3)~(8)。
3.3 优化结果
采用AD-DE 算法对密封舱进行结构优化,结构最大应力变化曲线如图5所示,目标函数优化曲线如图6所示。

图6 目标函数优化曲线Fig.6 Objective function optimization curve
由图5、6 可知,优化后密封舱的最大应力为154.6 MPa,满足强度条件155 MPa,优化结果为48.72 kg,比初始设计质量减少了34%。
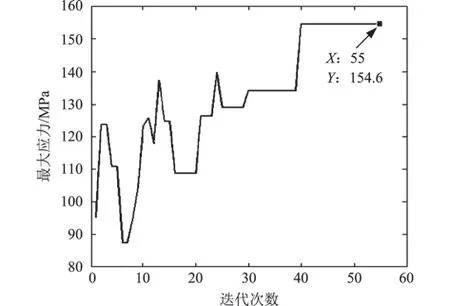
图5 最大应力变化曲线Fig.5 Maximum stress curve
4 结束语
本文提出的AD-DE 算法,采用自适应变异率和双重变异策略,同时引入函数T 来根据当前迭代次数动态的选择变异策略,使得算法在探索和开采之间取得动态的平衡,能够有效地避免陷入局部收敛。本文使用8个测试函数来对不同算法进行性能测试,其中6个高维函数,AD-DE 在不同的搜索维度下取得了5个最优值,2个二维函数均取得了理论最优值,同时迭代速度平均提速50%以上。表明AD-DE算法在求解精度和算法稳定性上均优于各对比算法。使用AD-DE 算法对某密封舱进行了结构优化,得到了较好的结构参数,优化后的结构质量比初始设计值下降了34%,从而说明了AD-DE 算法具有较好的实用性。
本文的工作提高了差分进化算法的性能;构建了基于Matlab-ANSYS的优化模块,为密封舱的结构优化设计提供了一种有效的方法。

