基于小波分解与SVR组合的风电场短期风速预测

白 鹏

(山西省信息产业技术研究院有限公司，山西 太原 030012)

0 引言

“十四五”期间，我国经济年均增速约为5.5%，预计到2025年全国电能消耗约在9万亿千瓦时～9.5万亿千瓦时,非石化能源占一次能源消费比重将达到19%～20%(55亿吨～56亿吨标准煤)[1]。可以说，可再生的清洁能源已经成为节能减排中至关重要的支撑性力量,未来新能源不再仅是补充和替代，而将成为能源供给侧的主力。

风能作为清洁能源的代表，因其无污染、零排放的特点被人们广泛地开发利用。风力发电的主要原理就是靠风力吹动风机叶片旋转，从而带动发电机工作。所以，风能质量的优劣直接决定了风力发电的电能质量。准确地预测预报风速是风电场运维调度人员充分利用风能的前提，同时也是避免瞬时极大风对发电机组造成震荡与损害的有效预防手段。根据风电场的实际需求，对风速的预测可以分为长期预测和短期预测。长期预测一般是在风电场规划建设之前，由勘测部门对风电场的气象环境做一段较长时期的观测，并结合气象学、地理学的相关理论对风电场全年或者某季度的风速做出推演性的预测。而短期风速预测则是对未来十几个小时甚至几个小时的风速进行精准预报。由于短时风速的随机性强且波动快，这就给风速预测带来了困难。国内学者对风速机理进行了大量的研究，提出了神经网络法、时间序列分析法、卡尔曼滤波法、遗传算法、灰色算法、小波分析法等研究方法[2-4]。但是单一的预测方法对于风速序列这样波动大、随机性强的数据预测效果并不理想,为此，本文建立了一种基于小波分解与支持向量回归机(Support Vactor Regression SVR)模型组合的风电场短期风速预测方法，该方法较单一预测手段有较高的预测精度。

1 原始风速序列的小波分解与重构

风速特性的观察记录表明，风具有紊流特性，即风向和风速在不停地发生改变，甚至在极短的时间内会有相当大的变化。故风速序列是多个频率序列的叠加，利用小波分解的方法可以将原始风速序列分解为多个特征序列,主要是利用Mallat金字塔算法[5]。

风速序列可由小波函数展开，分成低频部分与高频部分,可表述为：

(1)

其中:t为时间序号;f(t)为原始信号;k为分解的层数,j=0,1,2,…,k；H(·)、G(·)为时域中的小波分解滤波器；Aj为f(t)在第j层低频部分的系数；Dj为f(t)在第j层高频部分的系数。

小波的重构算法与分解相反，可表述为：

(2)

其中：h(·)、g(·)为时域中的小波重构滤波器。

小波基函数选取db家族小波基函数，因其具有紧支撑、大消失矩以及良好正则性等特点被广泛用于时序序列的特征提取中。本文选择db4小波基函数对原始风速序列进行分解，分解级数为三级。

2 支持向量回归机

将小波分解后的风速序列的分量作为输入量输入到支持向量回归机中进行风速分量的预测。支持向量回归机是人工智能发展的一大创新，因其泛化能力强，在工业上受到了广泛的运用。将支持向量机应用于回归问题求解，其根本就是要在整个空间内部找到一个最优的分类面，使得样本离分类面的距离是最小的。分类面的函数表示如下[6]：

y=ωΦ(x)+b.

(3)

其中：ω为权重；b为函数阈值；Φ(x)为高维非线性函数。

支持向量机问题可抽象为一个凸优化问题，即：

(4)

约束条件为：

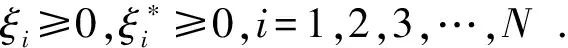
(5)

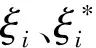
使用拉格朗日乘子法可以将式(4)和式(5)的凸优化问题转化为等价的对偶问题。设空间的样本集合为T={(xi,yi)|i=1,2,…,N}，则有：

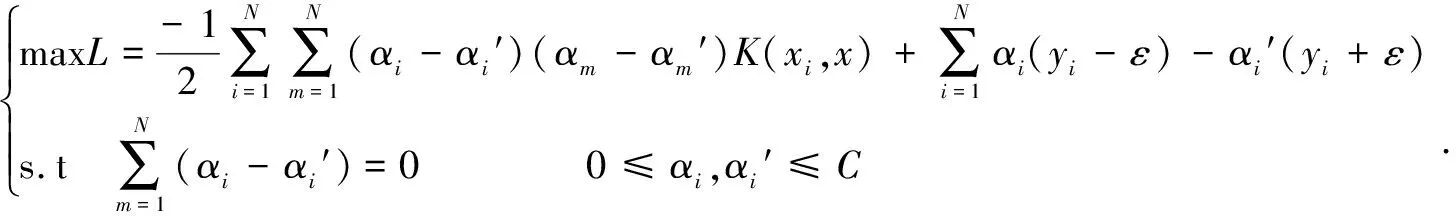
(6)

其中：i=1,2,…，N,m=1,2,…,N，i≠m;αi、αi′、αm、αm′为拉格朗日算子；K(xi,x)为核函数，此处选取Sigmoid 核函数。

利用支持向量回归机可以将风速的回归方程表示为：

(7)

3 组合预测的实现方法

将小波分解后的原始风速序列分量信号输入各回归向量机预测模型进行预测，然后将预测的数值进行小波尺度下的重构得到最终的预测数值。具体计算步骤如下：

(1) 首先对原始风速进行小波3层分解，得到分解后的分量。

(2) 将各分量输入支持向量回归机中，输出各分量的预测值。

(3) 对各分量进行小波尺度的重构。

(4) 得到最终的预测风速序列。

算法流程如图1所示。

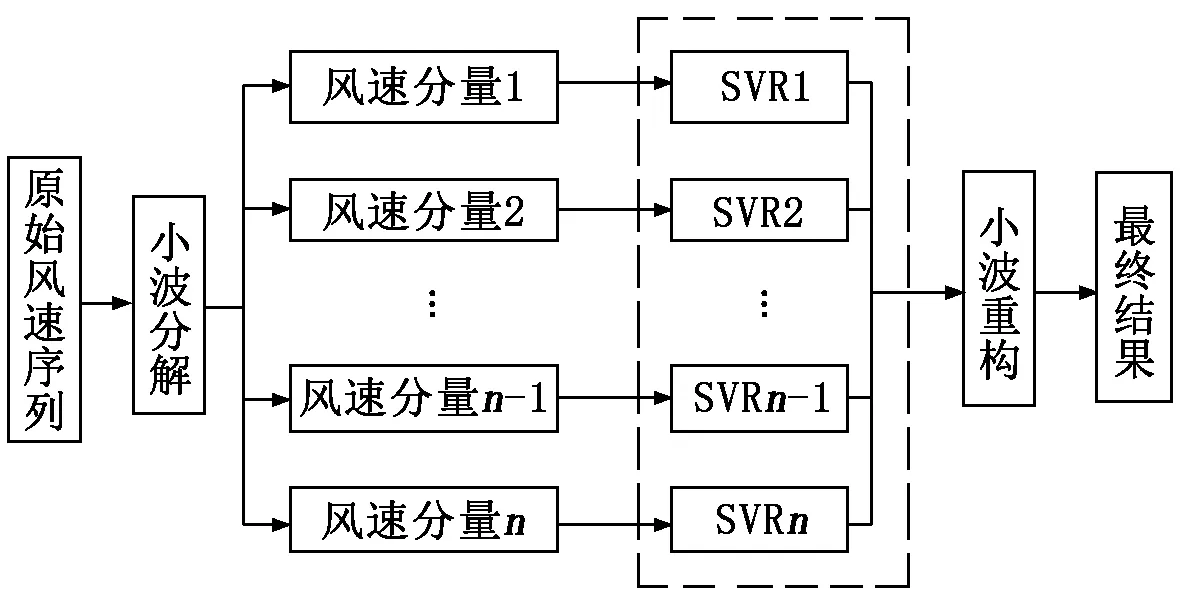
图1 算法流程

4 预测效果仿真

本文使用山西某风电场4月份某一天中的一段风速数据进行预测，采样间隔为1 min，共采样600个风速数据。利用db4小波基进行3层小波分解，分解波形如图2所示。

图2中，s为原始的风速序列，a3为分解后的低频分量，d1、d2、d3为分解得到的高频分量。由图2可以看出，通过小波分解手段，将原始序列的不同频域的分量投影到时域上，有利于风速序列的分析，分解后的低频序列波动较缓，而高频分量波动剧烈。

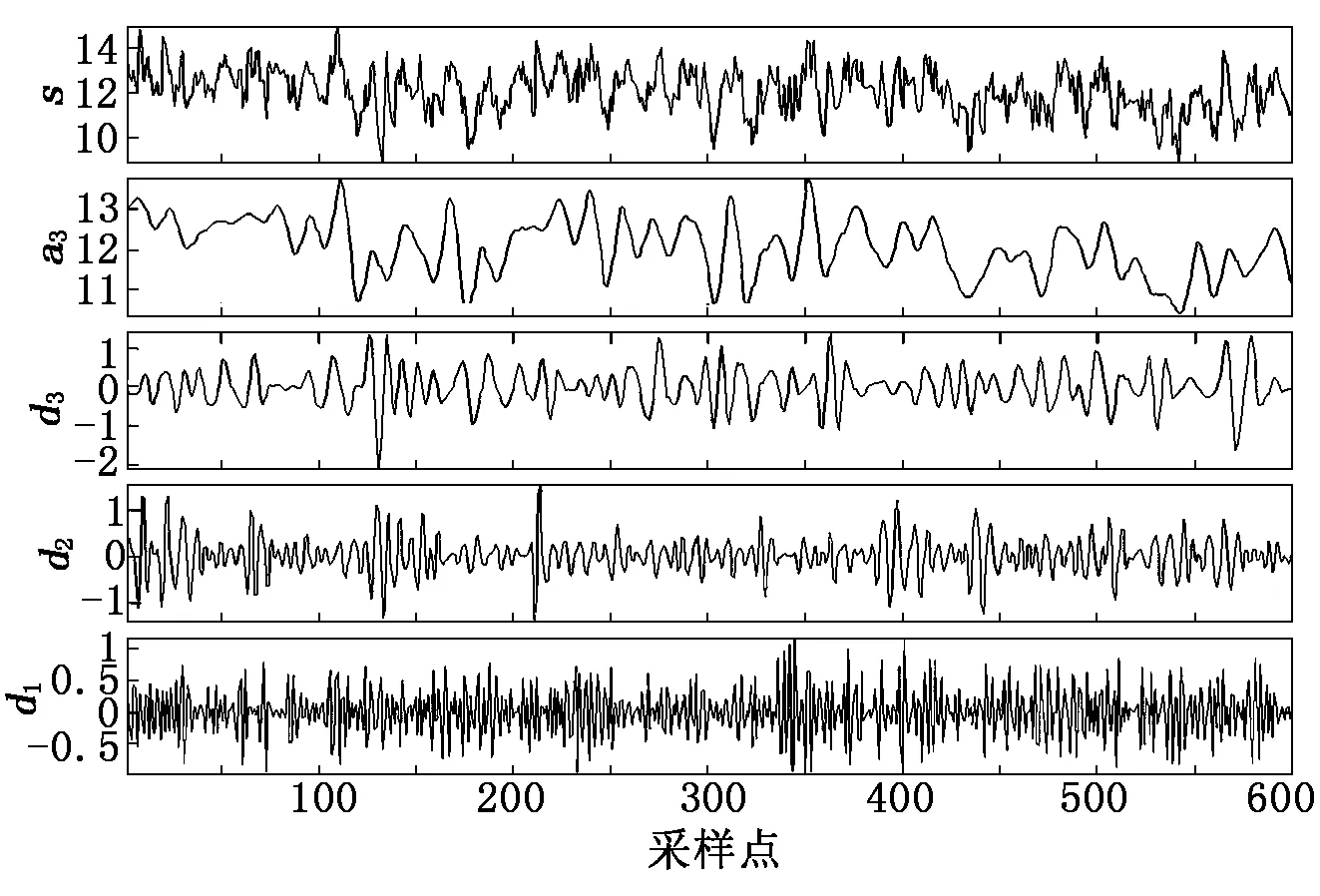
图2 原始风速序列的3层小波分解

将分解的风速分量输入支持向量机进行预测，采样频率为1 min，即每分钟采集一次风速数据。前550个数据作为风速的训练数据，后50个数据作为风速的预测数据，低频分量和高频分量的后50个数值的预测仿真曲线如图3～图6所示。

由图3～图6可以看出，SVR对风速序列做回归预测的效果还是比较准确的。因为SVR是基于风险最小原则建立的，就是要同时考虑经验风险与结构风险的最小化，在小样本情况下，能够取得比较好的回归效果。 SVR在保证分类精度的同时降低学习的VC维(Vapnik-Chervonenkis Dimension)，可以使学习在整个样本集上的期望风险得到控制，当核函数已知时，可以简化高维空间问题的求解难度。同时SVR是基于小样本统计理论基础，这符合机器学习的目的，具有较好的泛化推广能力。

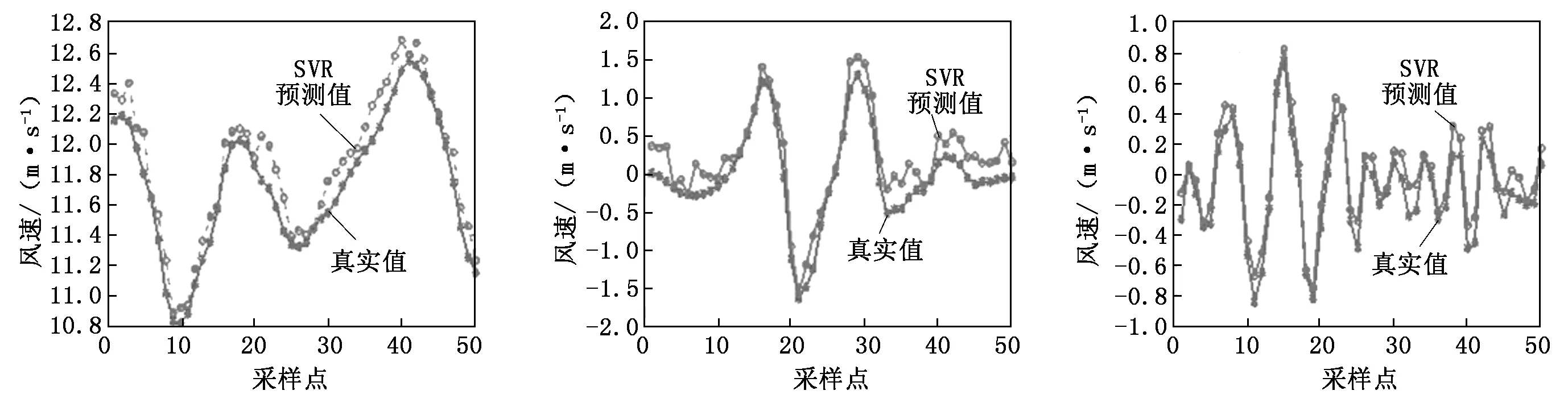
图3 低频分量a3的后50个点的预测效果图4 高频分量d3的后50个点的预测效果图5 高频分量d2的后50个点的预测效果

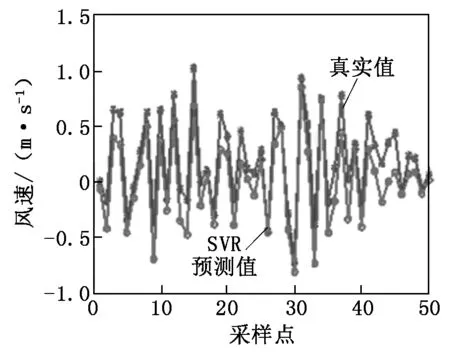
图6 高频分量d1的后50个点的预测效果

下一步是利用小波的重构属性将预测得到的高频、低频数值进行db4小波基函数尺度上的重构，将重构的数值与SVR直接预测得到的数值和真实值做比较，结果如图7所示。不同预测模型的误差比较见表1。

从图7中可看出，经过小波分解预测的结果要比直接用SVR预测准确，这是因为小波将风速序列进行了多尺度的分解，更能显示出风速序列的内在规律。用SVR分别进行预测是对每一种尺度下的风速序列的特点的预报，SVR回归机高度的泛化能力可以学习每一个尺度下的风速的特征，再经过重构后的总体预测结果比单独的SVR回归机更加准确。从表1不同预测模型的绝对百分比误差(MAPE)、均方误差(MSE)、均方百分比误差(MSPE)三个指标上也说明了这个问题。

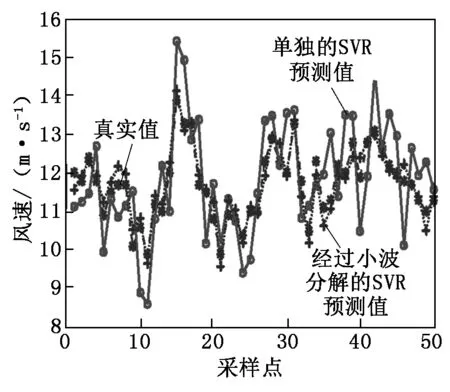
图7 重构后的预测比较

表1 不同预测模型的误差比较

由此可以看出，经小波分解的SVR组合预测模型在3个误差指标上均优于单独的SVR模型，有较高的预测精度。

5 结语

本文建立了经小波分解的SVR组合预测模型，通过将原始风速序列进行小波3层分解，得到每一种尺度下的风速，然后再用支持向量回归机(SVR)对每一个尺度的风速进行学习，最后将泛化好的SVR模型用于预测，并将预测分量进行小波重构得到最终的预测结果。经过仿真验证可得出，经小波分解的SVR组合预测模型预测误差比单独的SVR模型更低，预测的结果更加精准。