基于五轴球头铣削加工刀具朝向的抑制颤振方法研究

刘翔，景璐璐

（200093 上海市 上海理工大学 机械工程学院）

0 引言

与三轴铣削加工相比，五轴铣削加工除了X，Y，Z 三个方向的约束外，还多了2 个旋转自由度α和β，使得五轴铣削加工的加工参数不仅有传统的切削深度、主轴转速、进给量等，还有前倾角α和侧倾角β[1]。

对五轴铣削加工稳定性的研究主要包括2 部分工作：变轴向铣削动力学建模和铣削稳定性的判定。Tlusty[2]等对刀具方向问题进行了研究，提出了刀具方向能改变刀具和工件表面静态挠度的结论；Ozturk[3]等做了刀具前倾角和侧倾角对铣削稳定性影响的实验，通过零阶和多频稳定性方法生成系统的稳定叶瓣图作为选择合适前倾角和侧倾角的依据；Budak[4]等分析了五轴铣削的加工特点，建立了判定五轴球头铣削稳定性的数学模型，并且使用频域法对铣削稳定性进行了求解，分析了前倾角和侧倾角对铣削稳定性的影响；Wang[5]等研究了不同刀轴朝向下加工区域的变化，提出了在不同的刀轴朝向下加工区域的形状基本不变的结论。

铣削稳定性的判定主要分为频域法与时域法，频域法速度快，但是精度低，时域法计算复杂但是精度高。Altintas[6]等使用单频率法判定加工稳定性，但是该方法只适用于大切深的条件下，对小切深下的铣削稳定性预报误差较大；Bayly[7]等用有限元微分法计算对加工稳定性的极限进行了分析；Stepan[8]使用半离散法对铣削稳定性进行预报，该方法通过离散化的思想，求出相邻离散项的转移矩阵，并用Floquet 理论判定稳定性。

本文建立了刀具坐标系来描述刀具的螺旋角、浸润角、滞后角等参数，建立工件坐标系描述刀轴的前倾角和侧倾角，并且建立各自坐标系之间的转换关系。使用微元法对铣削力进行建模，使用实验法对铣削力系数进行计算。对动态铣削过程进行建模。考虑颤振的再生效应列出二阶时域微分方程，通过傅里叶变换将系统转换到频域内进行分析，得到输入输出与频率响应函数的关系通式。通过实验法测得刀具和工件各自的频率响应函数，并通过坐标系之间的转换关系计算接触区域的频率响应函数。最后，使用频率法对铣削稳定性进行判定。

1 五轴球头铣床铣削稳定性判定

1.1 坐标变换

图1 所示为定义的刀具坐标系。Z 轴为刀轴方向，用于描述刀具的螺旋角、浸润角、滞后角等参数，刀具的频率响应函数可使用感应锤沿着刀尖的法向和径向即XT和ZT方向进行敲击测得。

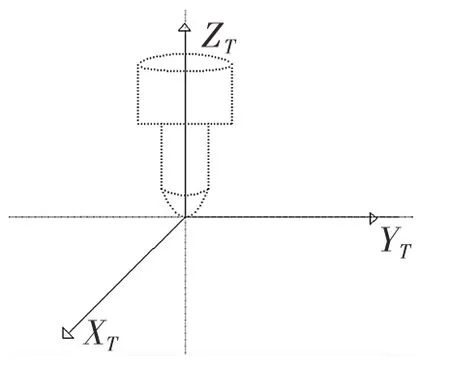
图1 刀具坐标系Fig.1 Tool coordinate system

图2 所示为工件坐标系。走刀的路径就是在工件坐标系中定义的，该坐标系是根据铣削加工后的刀路轨迹来定义的，其原点位于刀具铣削时所在的刀心位置，XW轴为刀路轨迹曲面在该点的切线方向，YW垂直于XW并且与其在同一工件平面内，ZW为刀路轨迹在该刀心点的法线方向。

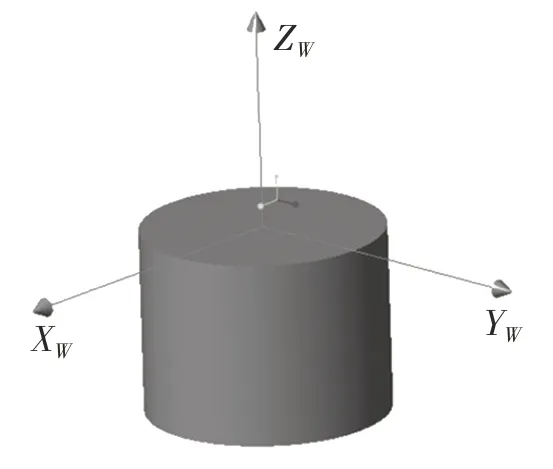
图2 工件坐标系Fig.2 Workpiece coordinate system

工件坐标系用于描述铣削加工后在工件表面留下的形貌，刀具包络面、刀具进给量、切削深度以及刀具倾角等参数，当刀轴有一定倾角时，施加在工件上的铣削力方向会改变，因此，要求出刀具-工件结合部的频率响应函数不能单纯对刀具和工件各自的频率响应函数进行叠加，而是应该进行一系列的换算。

首先当刀具没有任何倾角时，刀具坐标系和工件坐标系可以当成同一个坐标系，当刀具产生前倾角α和侧倾角β时，即刀具坐标系沿着X 轴和Z 轴分别旋转了α和β角度，故分别有如下旋转矩阵：

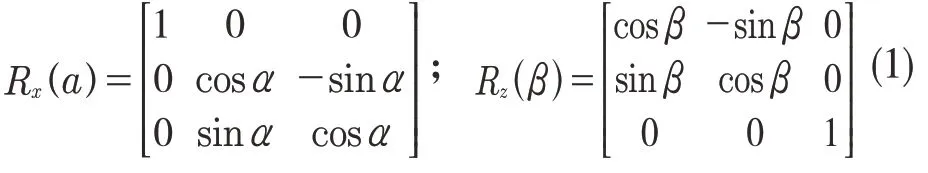
因此，从工件坐标系到刀具坐标系转换的旋转矩阵为

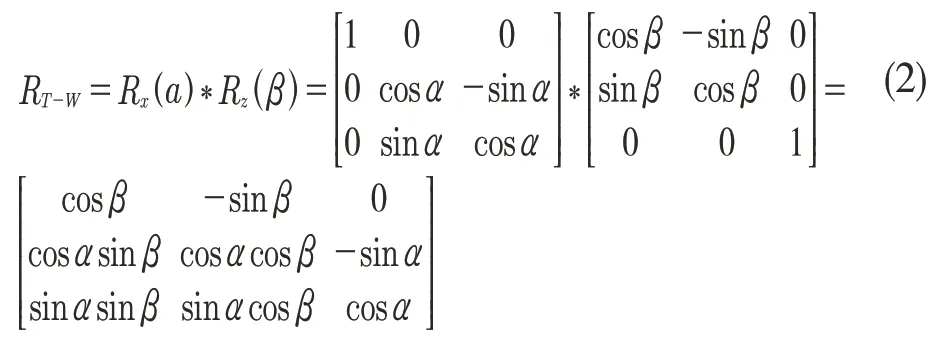
1.2 铣削力建模

对一般的铣削力进行建模，通常的处理方法是将球头铣刀微元化，本文采用Altintas 铣削力模型对铣削力进行研究[9]

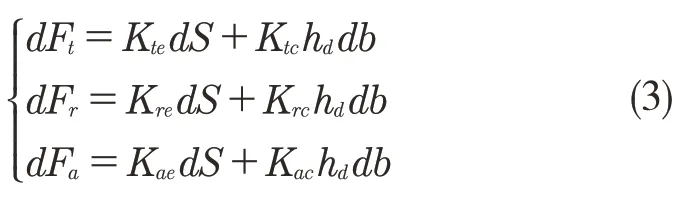
式中：dFt，dFr，dFa——微元上所受的单位切向力，单位径向力，单位轴向力；Ktc，Krc，Kac——切向力铣削力系数，径向力铣削力系数和轴向力铣削力系数；Kte，Kre，Kae——切向力刃口力系数，径向力刃口力系数和轴向力刃口力系数；dS——微元长度，hd——瞬时切削厚度，hd=fzsinφsinχ，其中fz表示刀具的进给率；db——微元的高度，

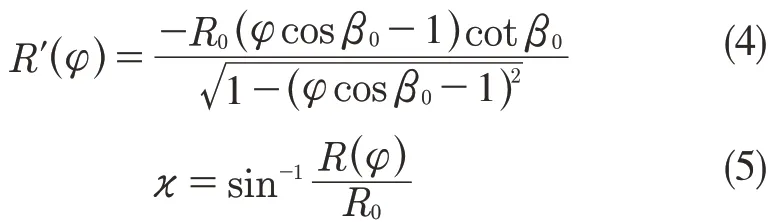
对3 个铣削力系数和3 个刃口力系数的计算是铣削力建模的关键，铣削力系数和刃口力系数主要通过实验法测得，下面简述其原理。

给定接触角、轴向切削深度，改变每齿进给量，做铣削实验，获取每个铣刀周期内的平均铣削力。为避免刀具偏心的影响，可以先测量主轴转一圈之后的总切削力，再除以铣刀刀齿数。

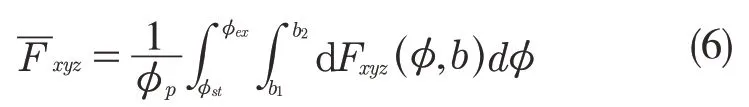
式中：φp——齿间角，φp=2π/N；φ——微元的瞬时齿位角；b1，b2——微元高度的上下限。

X，Y，Z 三个方向的瞬时铣削力可以表示为

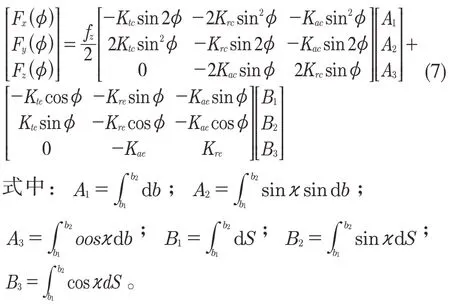
将式（6）和式（7）联立，可得到x，y，z三个方向的平均铣削力。

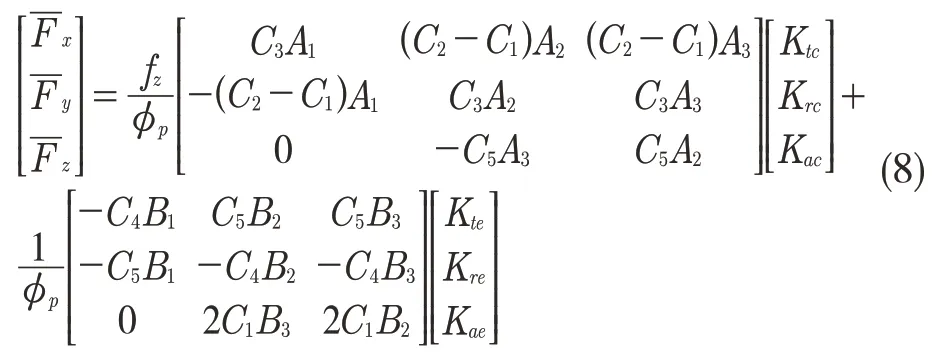
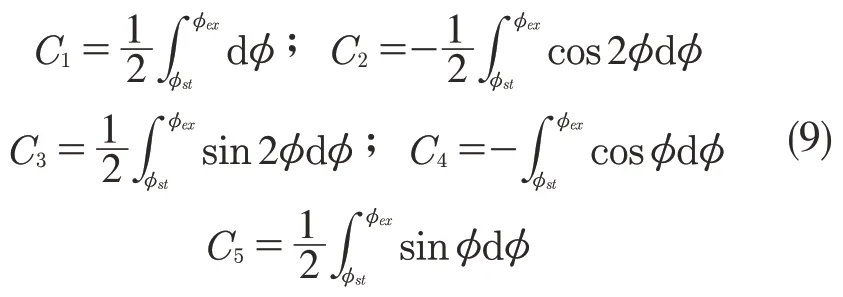
根据式（3），平均铣削力又可以表示为

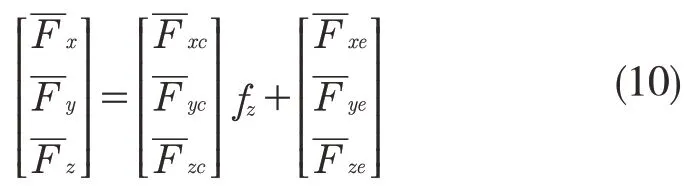
将式（10）代入式（8），即可求得铣削力系数和刃口力系数。

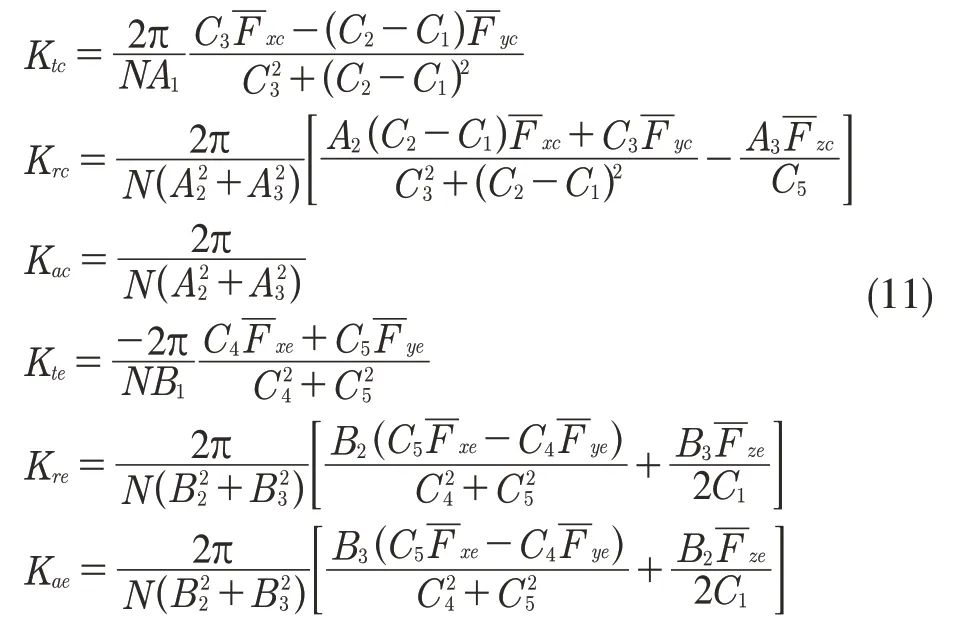
综上，将式（3）微元铣削力模型中所有的参数作了说明和求解。故单个微元上的铣削力沿x，y，z 三个方向的分量为

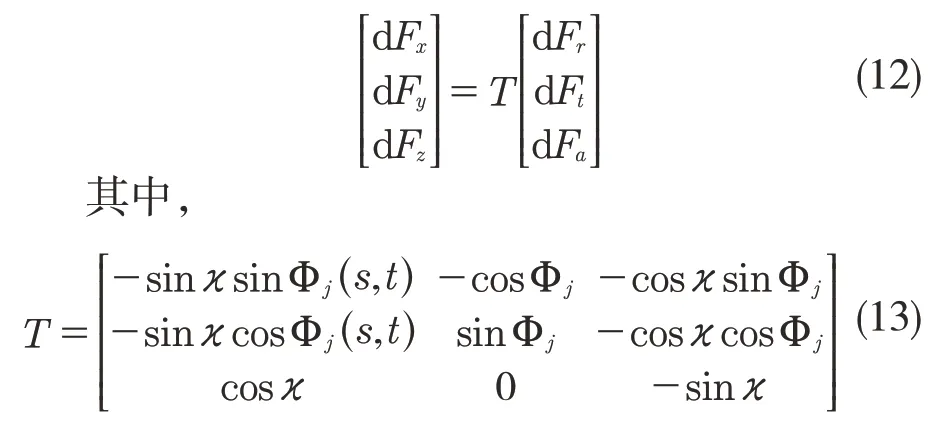
故由式（2）、（3）、（12）可得，瞬时铣削力在x，y，z 三个方向的分量为

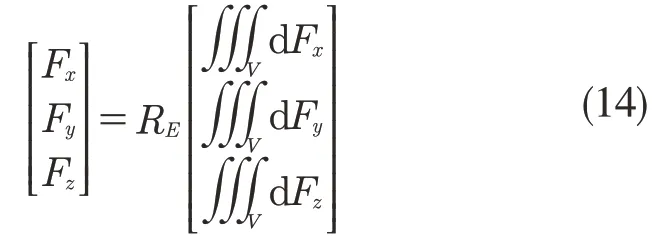
式中：V——铣刀与工件接触部分。

1.3 动态铣削过程建模

对于柔性刀具-刚性工件系统，可以将铣削过程看成一个多自由度的弹簧-阻尼系统，如图3 所示。

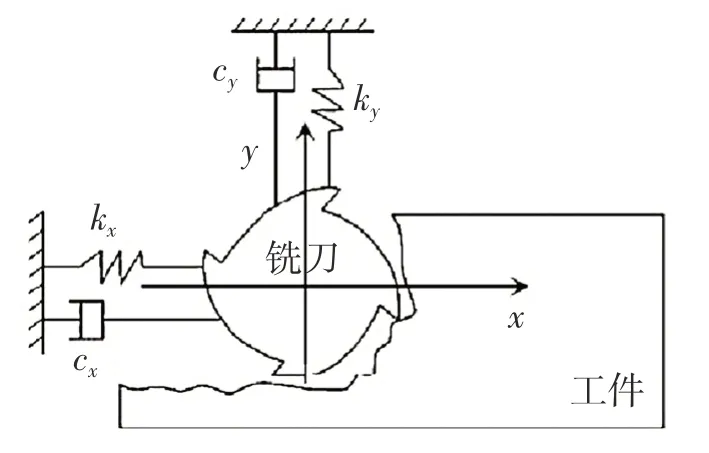
图3 铣削系统动力学模型Fig.3 Dynamic model of milling system

五轴球头铣削系统可以看成是X，Y，Z 三个方向的弹簧-阻尼系统，其运动微分方程可以表示为

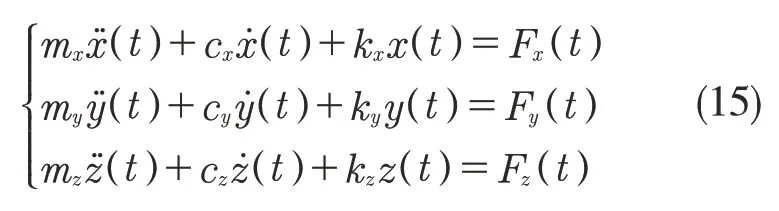
式中：x（t），y（t），z（t）——刀具在x，y，z 三个方向上的瞬时振动位移；m，c，k——质量，阻尼和刚度。

目前，在时域内判定系统的稳定性比较难实现，因为时域微分方程尤其是高阶微分方程很难求解，常用的方法是利用频率法来研究系统的动态稳定性。

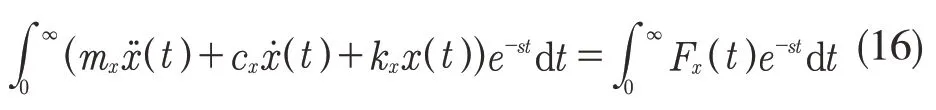
对等式两边进行整理，可得

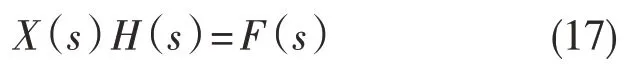
式中：H（s）——传递函数。

令s=jω，可得在频域内的动态铣削模型如下：

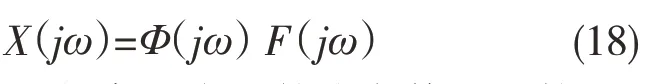
式中：Φ（jω）——频率响应函数或者传递函数。

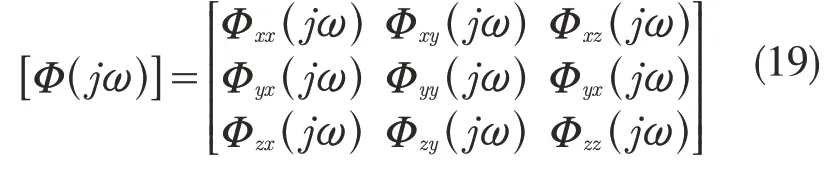
系统在t 时刻的振动矢量可以表示为

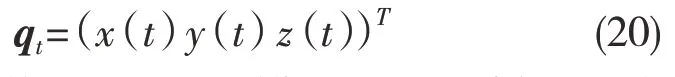
同理，系统在上一个周期即t-T 时刻的振动矢量为

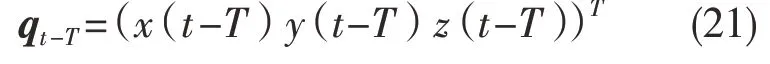
故

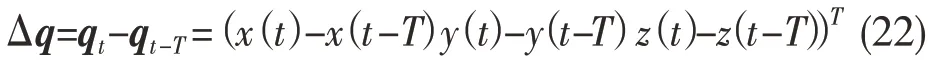
在频域内达到临界状态，即振动频率为颤振频率ωc时，此时的振动又可以在频域内表示为

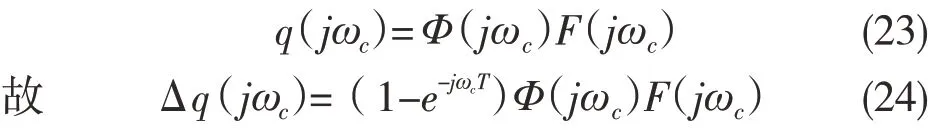
对式（3）式进行处理，可得动态铣削力的另一种表达形式：

将式（24）代入到式（25）中可得

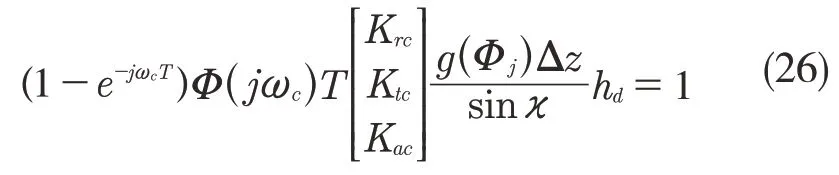
为方便计算，可将所有的已知量设为[A0]，令式（26）的行列式的值为0，即可得闭环铣削系统的特征方程

1.4 频率响应函数的转换

加工过程中，铣刀自身做旋转运动，工件自身做进给运动，因此刀具-工件结合部的振动在啮合坐标系中可以表示为

其中，ΦE即为刀具-工件结合部的频率响应函数。

同理，工件和刀具在各自的频域内传递函数为

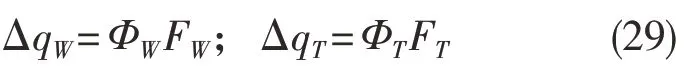
刀具-工件结合部的相对振动由二者叠加而成

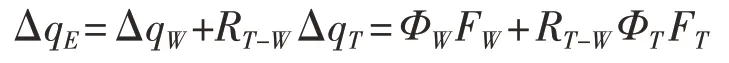
刀具-工件结合部的铣削力

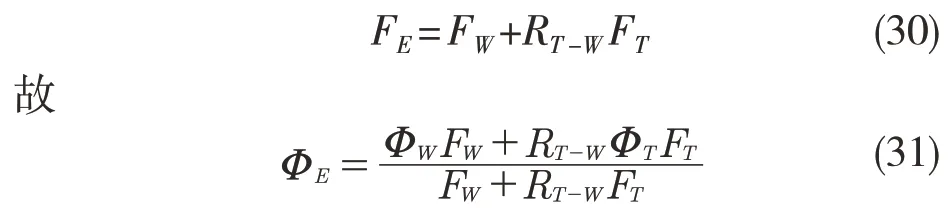
由式（31）可知，刀具-工件结合部的频率响应函数与刀具倾角有关。

1.5 铣削稳定性判定

铣削稳定性的判定，特别是稳定叶瓣图（LOBE 图）的绘制主要用到频域法和时域法。在频域内如果一个闭环系统是稳定的，它的充要条件是该系统的特征方程的根全部在复平面的左半平面。当然，直接解出特征方程的特征根仍然是不现实的，利用频域法能减少很大的计算量[10]。

将式（31）代入式（27）中可得

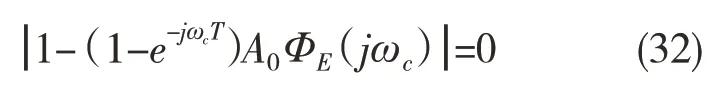
对于三阶系统而言，假设它的3 个根全在复平面的左侧，则当wc由0 逐渐变为∞时，系统的特征方程又可以写成

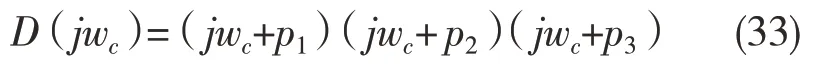
相角沿着逆时针的变化为

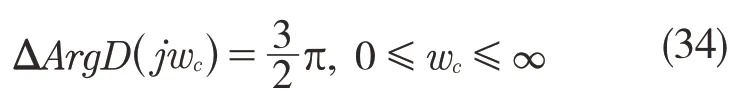
若3 个根有一个跟在复平面的右侧，此时，2 个在复平面左侧的根引起的相角变化为π，在复平面右侧的根引起的相角变化为，总的相角变化为而并非

通过频域法得出一系列的颤振频率wc，即可求得对应的临界轴向切削深度：

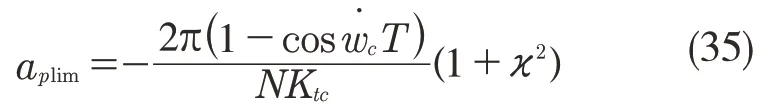
而主轴转速可以通过刀齿周期T 求得

1.6 小结

根据以上分析，对变轴向铣削稳定性分析的大致步骤如图4 所示。

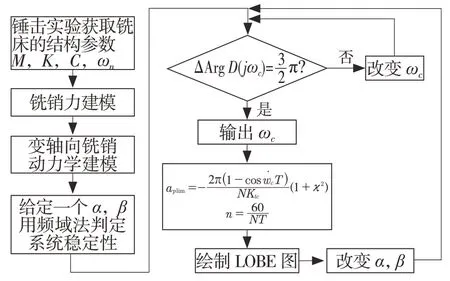
图4 铣削稳定性判定流程图Fig.4 Flow chart of milling stability judgment

2 结论

五轴球头铣削加工过程由于球头铣刀的灵活性，使得可变的加工参数增加了前倾角α和侧倾角β。本文首先定义了工件坐标系和刀具坐标系来分别描述球头铣刀的刀轴位置和铣刀自身的参数，并且给出了2 个坐标系之间的转换矩阵；其次，使用微元法对铣削力进行建模，并且对铣削过程进行建模；最后，使用傅里叶变换将铣削过程数学模型转换到频域内，利用频域法对铣削稳定性进行判断。