改进蚁群算法在机器人路径规划中的应用

何雅颖，范昕炜

中国计量大学 质量与安全工程学院，杭州310018

机器人路径规划是指根据已知障碍环境，自行规划出一条从起始点到达终止点无碰撞的最优路径[1]。其中传统方法包括栅格法、A*算法[2]、人工势场算法[3]等。随着智能群算法的发展，遗传算法[4]、粒子群算法[5]、蚁群算法等也开始应用于路径规划中。

蚁群算法（Ant Colony Optimization，ACO）是由意大利学者Dorigo等[6]提出的一种仿生蚂蚁觅食的智能群算法，具有正反馈、并行性、强鲁棒性和较好适应性的特点，但同时也具有易陷入局部最优、收敛速度较慢和易陷入死锁等问题。其中信息素对算法结果具有重要影响，不少学者通过信息素不同的设置方式来优化算法。文献[7]提出非均匀信息素分布划定起点到终点两个点为顶点的矩形区域为有利区域，提高该区域的初始值。该方法能有效防止蚂蚁在初期向目标点反方向搜索，但是区域内信息素并没有差别，改进效果有限。文献[8]提出双层蚁群算法，先通过外层算法求取最优解延伸其解空间，后利用内层算法进行局部寻优，如果在此空间内找到更优路径则执行信息素二次更新。该方法虽然提高了最优解的可能性，但是仅限于有限空间探索，算法可能陷入局部最优。文献[9]引入了最优解与最差解改进信息素更新规则，增强当前最优路径的信息素，减弱最差路径的信息素。该方法有效加快了收敛速度，但同时也减少了种群的多样性，不利于最优解的获取。文献[10]提出在算法搜索过程中加入人工势场局部搜索寻优算法，将人工势场中力因素转换为局部扩散信息素，算法有效减少了交叉路径与蚂蚁“迷失”数量，提高了蚁群对障碍物的预避障能力，但算法结构设计较为复杂，环境适应能力有待提高。文献[11]将遗传算法与蚁群算法相融合，提出利用遗传算法生成初始路径，将较优路径作为蚁群算法初始信息素的参考信息，减少初期算法盲目性，后利用蚁群算法对初始路径进一步优化。该改进算法能避免局部最优，但算法运行时间较长。

综上所述，信息素的设置能有效提高收敛速度，但同时也有可能降低算法寻优能力，不利于获取最优解。为平衡寻求最优解与算法收敛速度，提出改进的蚁群算法，其中包括：对初始信息素进行非均匀分配，提高收敛速度；提出局部分块优化策略优化子区域路径提高求解质量；利用信息素增强因子保留更优解，避免陷入局部最优；引入反向学习对信息素进行优化，改进状态选择概率，提高算法全局寻优能力。

1 相关知识

1.1 蚁群算法

1.1.1转移概率

在t时刻蚂蚁m从节点i到节点j由式（1）计算转移概率并根据轮盘赌法则对下一路径点进行选择。

式中，τij(t)为路径(i,j)间的信息素含量，α为信息素启发因子，ηij(t)为期望启发项，通过式（2）计算可得；d(i,j)为路径(i,j)间的欧式距离，β为期望启发式因子。α和β分别代表信息素、期望启发项的重要程度。allowedm表示蚂蚁m所有下一可行节点集合。

1.1.2信息素更新

每只蚂蚁在行走过程中都会留下一定量的信息素，随着迭代次数的增加，信息素不断地增加，同时也在不断挥发。所有蚂蚁完成一次迭代后，会对残留信息素进行更新，根据式（3）、（4）更新信息素。

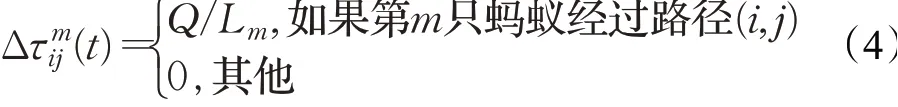
式（3）中ρ为挥发系数，Δτij为本次迭代中路径(i,j)的信息素增量，W为蚂蚁总数，为本次迭代中第m只蚂蚁在路径(i,j)留下的信息素。式（4）中值的计算采用的更新方式为蚁周模型，除此之外还有蚁量模型和蚁密模型。式中Q是一个常数，表示信息素强度值，Lm表示第m只蚂蚁在本次迭代中所走路径总长度。

1.2 反向学习

反向学习的概念于2005年由Tizhoosh[12]提出，后被成功用于算法的进化，解决优化问题。以下为反向解定义。

定义1假设x是一维空间的一个实数，x∈[a,b]，因此x反向解为[13]：

定义2假设P=(x1,x2,…,xD)为D维空间中一点，其中xi∈[ai,bi],∀i∈{1,2,…,D},则其反向解为Pˉ=

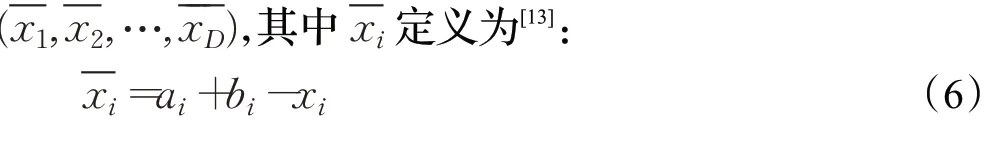
2 改进蚁群算法

2.1 非均匀初始信息素分布

蚁群算法中，蚂蚁主要根据栅格间信息素的差异寻求最优路径，而在传统的蚁群算法中，初始信息素采用的是均匀分布，因此每只蚂蚁的状态转移概率只取决于期望启发项，而栅格间期望启发项差异较小，因此初期算法由于缺少信息素引导具有盲目性，且搜索速度较慢，最终影响解的质量与收敛速度[14]。因此对初始化信息素进行非均匀分布处理，提高栅格间信息素的差异能有效提高搜索效率。为避免改进后的初始信息素过度或者错误引导后续蚂蚁探索最优解，信息素的非均匀分布仅针对区域进行差异处理而非单个栅格点，即只提高有利区域内的初始信息素，降低算法陷入局部最优的可能。由于最优路径多集中于起点S至目标点E的连线附近区域，其区域范围受障碍物影响，以起点S和目标点E连线作x轴，以连线中点作为原点建立坐标系，以起点至终点距离dSE为长轴，全局优选区域距离ddiff为短轴建立椭圆，其计算公式如式（8）。在该椭圆内的区域为全局优选区域R，并提高优选区域R内的路径点初始信息素，而不在该范围内的路径点则保持原初始信息素值τ0。非均匀初始信息素分布规则如式（7）所示：

式（7）中τ0为信息素初始值，C为全局优选区域信息素增量。式（8）中ddiff与地图障碍物有关，ξ为环境障碍物占比，ξ越高，则ddiff越大，全局优选区域范围更广；r和c分别表示矩阵地图的行数与列数。

2.2 改进信息素更新规则

信息素的更新包括对原有路径上信息素的挥发与新增路径信息素的积累，因此提出局部信息素分块优化策略对信息素的更新规则进行了改进。

在传统蚁群算法中，所有的蚂蚁完成当前迭代后将对蚂蚁路径进行更新。路径的好坏评价取决于全局路径的长度，而忽略了对局部区域路径的评价。图1中实线路径与虚线路径分别代表历史最优路径和当前迭代最优路径，横坐标x∈[0,5]时，当前迭代最优路径更短；而在x∈[5,20]时，历史最优路径更短，因此提出局部信息素分块优化策略。算法初期并不知道路径将会经过哪些路径点，无法利用具体坐标作为分割依据，因此将矩阵地图按x坐标以一定间隔步长n纵向切割均匀划分为多个区域，n越小容易造成路径曲折较多，不利于寻求最佳路径，n较大则达不到分块优化的效果。如图1所示矩阵地图被以步长n=5划为4个区域，有多个点都经过同一切分线时，以最后经过点作为终止点。随后引入精英蚂蚁[15]的策略，当所有蚂蚁完成当前迭代后，对各区域内的最优局部路径信息素进行更新。全局最优路径本质上是由各个局部最优路径组合而成的，对局部最优路径信息素的更新旨在引导后续蚂蚁行驶至该区域内的路径选择，一旦蚂蚁行驶至该区域最优路径附近则能通过此策略更大概率选择最优路径点。但局部区域路径优劣如果仅从区域内路径长度考虑，很容易导致区域内水平方向的路径被认为是最优而非更接近终点的路径，因此路径长度考虑其路径段与起点和终点的总距离，如式（9）所示。同时由于非均匀初始化信息素的改进，对局部路径长度的选择也更有利。

图1 信息素分块优化Fig.1 Pheromone block optimization

因为局部更新只是针对局部区域，缺乏全局信息素引导，所以对每个区域内最优路径更新后，再对蚂蚁的全局信息素进行更新。鉴于此前已经对局部最优路径进行了更新，为了避免信息素重复叠加，只对全局最优路径信息素进行更新。局部最优路径更新规则与全局最优路径更新规则相同，如式（9）和式（10）所示。

式中，当计算局部最优路径信息素时，Lbest为各个区域内最优路径长度，Ldist为各局部区域内最优路径段长度，Lds为路径段第一个路径点到起点距离，Lde为路径段最后一个路径点到终点距离。在计算全局最优路径信息素时，Lds和Lds都为0，则Lbest为全局最优路径长度。

如果只对最优路径进行更新，随着迭代次数增加，最优路径上的信息素累积越来越多，高浓度的信息素含量会导致即使迭代后期出现了比历史更优路径，这条新路径上释放的信息素仍然远远少于现有最优路径上的信息素，容易陷入局部最优且可能在迭代收敛时丢失该解[16]。针对该问题，在信息素更新规则中引入信息素增强因子r，当出现比历史更优的路径时，通过增强因子提高此路径上的信息素，如式（11）所示。增强因子r随着当前迭代次数Nc的改变而发生改变，初期r值较小，避免信息素过量叠加防止算法陷入局部最优，后期值较大，加快收敛，如式（12）。

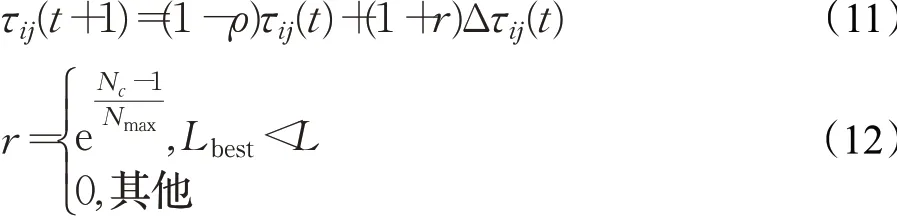
式中，Nmax为迭代总数，Lbest为当前局部区域或全局最优路径，L为历史最优路径。

2.3 改进状态转移概率

反向学习的主要思想在于对一个可行解，同时评估其反向解，对比后选择较优解。蚁群算法的正反馈机制不适用于完全解[17]，因此反向学习更适用于扩展蚁群算法解空间而非评估反向解，通过反向学习增加解空间覆盖率达到提高求解质量的效果。文献[12]提出基于反向学习的蚁群系统用于解决TSP问题，文献[16]提出反向蚁群优化算法解决故障诊断监控参数优化问题。

参考以上文献，引入反向信息素改进蚁群算法状态转移概率，用于路径规划寻求最优解。根据反向学习的定义，反向信息素计算如下式：

此时的信息素τij为局部和全局更新完毕后的信息素，分布优化策略已结束，因此式（13）中Lgbest为全局最优路径长度。第一次迭代过程中不会产生Lgbest，因此第一次迭代时的值为初始信息素。其中确定反向信息素的值为初始信息素τij(0)和最优路径长度Lgbest，因为信息素的积累由初始信息素和最优路径长度共同决定。

当蚂蚁m在t时刻进行路径点选择时，其转移概率为：

式中，λc为反向概率，λc∈(0,1)，λ为随机数；当λ<λc时，使用反向信息素计算选择概率，当λ>λc时，选择概率为原公式计算值。d(j,e)为下一节点j到终点e的欧氏距离。

3 改进蚁群算法的应用步骤

步骤1建立矩阵栅格地图，设置起始位置起点S与目标点E；初始化参数，包括信息素启发因子α，期望启发式因子β，挥发系数ρ，蚂蚁总数W，迭代总数Nmax，信息素强度值Q，反向概率λc，信息素初始值τ0与初始信息素增量C。

步骤2初始信息素非均匀处理。通过式（8）确定ddiff，计算全局优选区域R的范围，并根据式（7）对初始信息素非均匀处理得出τij(0)。

步骤3路径点选择。将W只蚂蚁放置于起点处，初始化禁忌表、路径点、路径长度，并将起点加入禁忌表中。根据式（14）和（15）计算每一只蚂蚁下一路径点选择概率，通过轮盘赌选择下一个节点，并将该节点加入禁忌表中。

步骤4判断蚂蚁是否到达了终点，如果没有，则返回到步骤3直至到达目标点为止。否则执行步骤5。

步骤5局部信息素分块更新。当所有蚂蚁完成当前迭代后，对所有地图进行分块处理，并分别计算每个区域的最佳局部路径，按式（9）、（10）和（11）分别对每个区域进行信息素更新，此时Lbest为每个区域最优局部解。当出现更优解时，按照式（12）计算增强因子并代入式（11）中进行计算，L为每个区域历史最优路径。

步骤6全局信息素更新。在局部区域信息素更新完毕后，按式（9）、（10）和（11）对全局信息素进行更新。此时Lbest为全局最优解。当出现更优解时，按照式（11）计算增强因子并代入式（11）中进行计算，L为全局历史最优路径。

步骤7反向信息素更新。按照式（13）对反向信息素进行更新，式中Lbest为全局最优解。

步骤8判断是否达到最大迭代数。如果达到最大迭代数则输出当前最优全局路径，如果没有，则清空禁忌表，并将迭代次数加1，重复步骤3到步骤7，直到达到最大迭代数。

4 模拟实验和分析

为验证改进蚁群算法的有效性，在MATLAB 2018b上进行仿真实验，操作系统为Win10（64 bit）操作系统，CoreTMi5-10210U处理器，16 GB运行内存。仿真实验采用两组对比实验，分别为20×20、30×30的栅格地图，并在相同地图下将本文改进蚁群算法与传统蚁群算法、文献[8]算法结果进行对比分析。

4.1 参数选取

蚁群算法参数多利用经验值取值，并利用多次对比结果选取最佳参数，但算法参数还涉及局部分块优化的步长n，因此基于以上参数，取分割步长n=1,2,…,c（c为地图的列数）在随机20×20、30×30地图上进行实验。其余仿真参数设置为：α=1,β=7,ρ=0.2,W=50,Nmax=

从20×20仿真结果图2（a）来看，n∈[4,6]时，即将地图分为4~5个区域效果较好，当n较小时，迭代次数比不分块更高，算法信息素分布分散，难收敛，无法找到较优值，因此路径长度也比不分块更长。随着n的增加，虽然迭代收敛次数有时能较快收敛，但是算法也容易陷入局部最优。从30×30的仿真结果图2（b）也可以看出这一点，当n∈[4,7]时，对应将地图分为4~5效果较好，n过长或过短都将影响收敛与最终结果，造成收敛速度与局部最优解的矛盾。基于此，对20×20和30×30都分为4块，20×20地图取n=5，30×30地图取n=6。

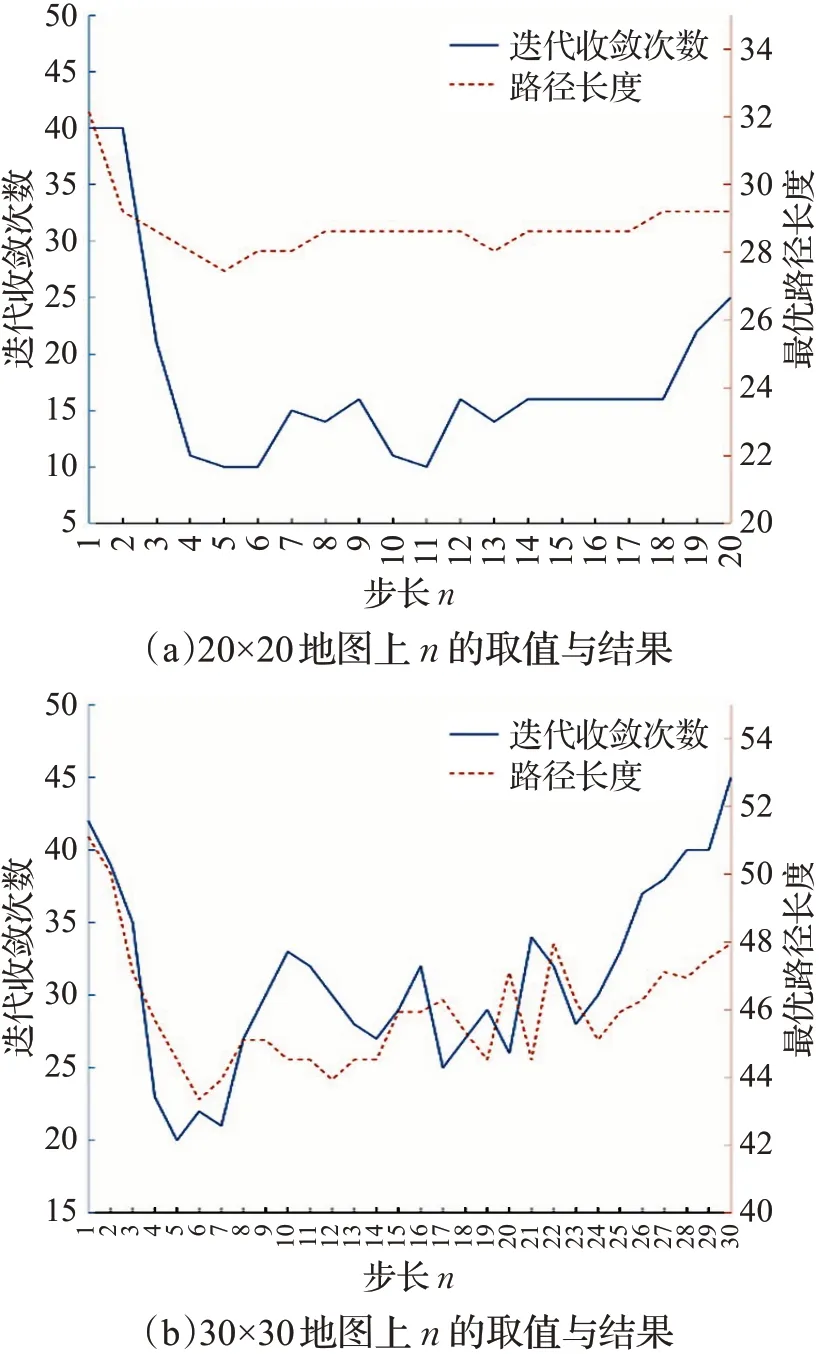
图2 n取值对结果的影响Fig.2 Influence of n value on results

4.2 20×20地图实验仿真

在20×20栅格地图下，分别对传统蚁群算法、文献[8]、本文改进算法进行仿真，路径仿真分别如图3和图4所示。最终实验数据如表1所示：传统算法路径规划长度为32.866，文献[8]规划长度为33.452，本文改进算法规划长度为28.038。本文算法较另外两种算法路径规划长度更短，拐点更少，对比传统算法与文献[8]算法，路径长度分别缩短了14.6%和16.2%，拐点分别减少66.6%和75.0%。传统蚁群算法收敛次数为21次，文献[8]为5次，本文改进算法收敛次数为12次。虽然文献[8]收敛次数为5，但是其求解质量明显低于本文改进算法，这也说明本文在算法收敛速度与求解全局最优解上平衡得更好。传统蚁群算法在迭代后期丢失最优解，最后收敛为局部最优值，而由于本文引入了增强因子r避免了这一问题，保留了最优解，避免了陷入局部最优。

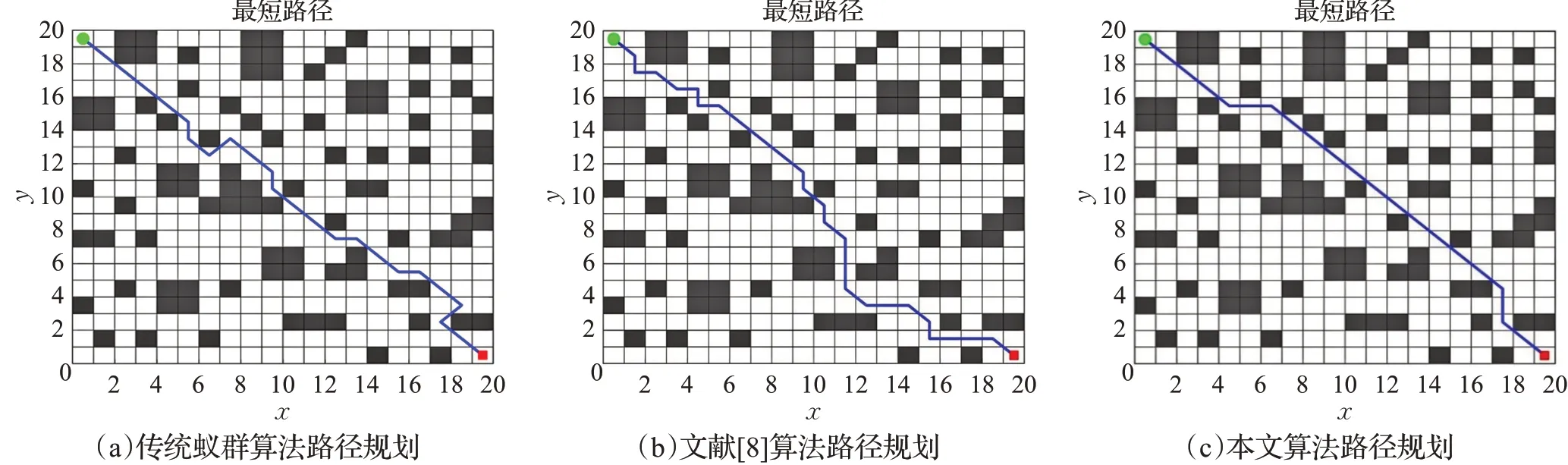
图3 20×20环境下四种算法仿真结果Fig.3 Simulation results of four algorithms in 20×20 environment

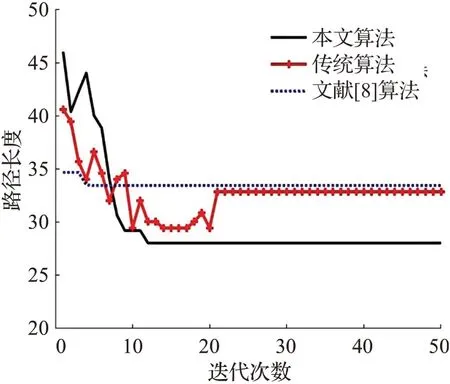
图4 各算法路径收敛曲线Fig.4 Convergence curve of each algorithm path

表1 20×20环境下各个算法结果对比Table 1 Comparison of results of various algorithms in 20×20 environment

为进一步验证各个改进环节的有效性，分别对每个环节改进和本文整体改进在20×20栅格地图下进行独立实验，实验结果如表2所示。初始化与分块策略这一改进环节对比传统蚁群算法有效减少了迭代次数，同时找到了更优解。反向学习信息素的引入对比传统算法也有效提高了算法的全局寻优能力，避免陷入了局部最优，但也由于缺乏信息素引导，导致迭代次数较多。而本文的改进方法综合以上步骤，结合了收敛速度的提升与全局寻优能力上的改进，能在较少的迭代次数内找到更优解，同时曲线更平滑，路径拐点数更少。

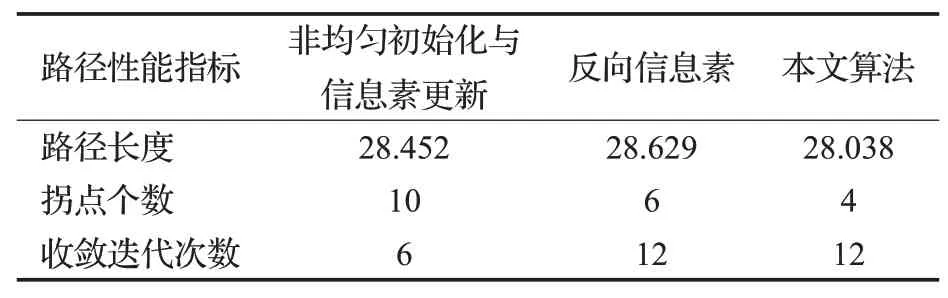
表2 20×20环境下各改进环节结果对比Table 2 Comparison of results of improvement steps in 20×20 environment

4.3 30×30地图实验仿真

在30×30复杂环境下，实验仿真结果如图5和图6所示。随着地图的复杂度增加，三种算法收敛迭代次数都有所增加，传统蚁群算法收敛曲线波动较大，算法稳定性较差，且依然陷入了局部最优。文献[8]虽然对比传统算法结果更优，但由于该算法仅针对于最优解拓展出来的小区域进行局部优化，缺少全局探索，因此也陷入局部最优。最终实验数据如表3所示，综合指标来看，本文改进算法在复杂环境下也有不错效果。最优路径长度上来看，本文改进算法路径长度对比传统蚁群算法和文献[8]分别缩短了14.1%和7.9%，拐点个数减少63.3%和60.0%，迭代次数减少23.0%和39.3%。在30×30地图上也对各个步骤的改进进行了验证，如表4，其结果与20×20地图结果类似，再一次验证了本文算法的有效性与优越性。

图5 30×30环境下四种算法仿真结果Fig.5 Simulation results of four algorithms in 30×30 environment

图6 各算法路径收敛曲线Fig.6 Convergence curve of each algorithm path

表3 30×30环境下各个算法结果对比Table 3 Comparison of results of various algorithms in 30×30 environment

表4 30×30环境下各改进环节结果对比Table 4 Comparison of results of improvement steps in 30×30 environment

5 结束语

本文针对传统蚁群算法存在易陷入局部最优、收敛速度慢等不足，提出改进蚁群算法。首先根据地图的障碍物占比以及矩阵地图大小构建全局优选区域，对初始信息素进行差异化处理，提高区域内信息素初始浓度而非具体栅格点信息素浓度，避免陷入局部最优的同时提高了收敛速度；利用局部信息素分块优化策略对矩阵地图进行分块处理，分别对各个子区域进行寻优并更新最优路径信息素，后对全局路径进行寻优，更新最优路径信息素。为避免只更新最优路径信息素，丢失更优解，在信息素更新公式中引入增强因子，保留更优解，避免收敛于次优解。最后应用反向学习优化信息素，改进状态选择概率，拓展了解空间，提高了全局搜索能力。实验结果表明，改进后的算法明显提高了收敛速度，寻优能力更强。对初始化非均匀分布的处理、信息素更新规则的改进以及反向学习在蚁群路径规划上的应用对比传统算法均有明显的改进，进一步验证了算法的有效性与优越性。