统计课程中大学生自主学习能力的培养

蔡亚玮,王 哲, 李雪梅, 李兰会,*

(1.河北农业大学动物医学院,河北 保定 071001；2.河北农业大学动物科技学院)

当今世界日新月异，社会竞争愈演愈烈。要跟上时代步伐，必须拥有自主学习的能力。很多专家学者表示，“培养学生的自主学习能力是教育的重要目标”，实际上，国内相关研究表明，“目前我国大学生自主学习能力仍普遍较低”，作为当代大学生，我们必须努力培养较强的自主学习能力和终身学习的观念，争取为国家未来建设添砖加瓦，责无旁贷。本文选取《生物统计与试验设计》课程作为研究背景，探究大学生在统计课程中自主学习能力的培养。

生物统计课程作为全国高等学校药学类专业的必修课，是一门以计算机软件应用为基础，融合概率论、数理统计和相关学科于一体，对医药、生物等相关领域研究对象的数据资料进行收集整理和分析推断以显示其总体特征和统计规律的多学科交叉的应用型课程。假设检验为该课程的核心内容，课程内容由先行课程—《数理统计和概率论》中的概率分布为基础，以小概率不可能原理作为基本思想展开假设检验的知识体系。在体系的构建过程中，以生产科研实践生活中的实际案例作为学习背景，利用统计分析软件SPSS或Excel建立数据库，在数据分析、模拟的过程中，将枯燥无味的数学公式转化为生动形象的表格图像，锻炼学生逻辑思维能力的同时，也会引导学生更加主动、自主的进行学习与探究。下面将以统计课程的二项分布和检验内容为背景展开讨论。

1 案例实现抽象概念的直观领悟

在医药模型中，许多试验只有相互对立的两个结果，如药物疗效结果，有效或无效；毒性检验的结果，存活或死亡等。在这种每次试验只有两个对立结果的多次独立重复试验中所显示出的概率分布称为二项分布。在本部分学习中，老师先引入一个事例，“设某村庄爆发流行性感冒，人们受感染的概率为20%，求只有6人被感染的概率”，在这样一个特定的条件下，我们利用SPSS中的概率函数PDF.BINOM进行探究，先假设该村庄有n=30人，在SPSS的[函数和特殊变量中]中选中二项分布的概率函数：Pdf.Binom，根据函数提示说明，依次输入参数值：6,30,0.2，点击确定，即可得到概率P(X=6)的值P为0.17946。为了更加深入地理解其内在规律，我们不断改变题目中的被感染人数，由6变大或变小，并利用Excel将P(X=k)与k的数学关系形象化到图像上，由图像变化不难发现，对于固定的样本量n与感染率p，二项分布的概率P(X=k)先随着k的增大而单调增大至最大值，后单调减少。此外我们仍基于题目背景，不断改变n或p值，使其一为变化值，另一为固定值，计算得到不同情况下对应的概率P(X=k)值，然后利用X和P值构建二项分布散点图，图1为固定p为0.2，n值不同的系列二项分布图；图2为n值固定为20，p值不同的系列二项分布图。

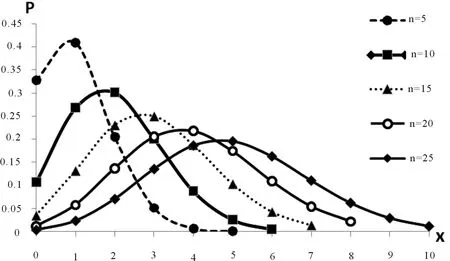
图1 n不同，p=0.2的二项分布图

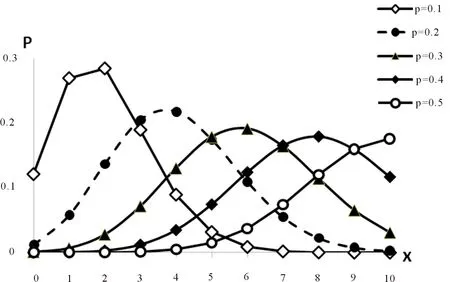
图2 n=20，p不同的二项分布图

通过对散点图的分析我们不难观察出n或p中任一值变化时二项分布曲线特征的相应变化。通过这一部分的学习，在教师的引导下，我们动手参与到课程学习中，观察到数字变化与图像特征的关系，潜移默化中我们不仅领悟了什么是二项分布，学会了二项分布的概率计算，还利用统计工具深刻理解了二项分布图像的由来、特征及其变化规律。

2 函数运算解决实际问题

在对二项分布基本概念和概率计算理解掌握的基础上，老师引导我们以概率为基础进行推断，为课程核心内容假设检验和统计推断作良好铺垫。以前文题目进行拓展，“该村庄有30人，其中20人被感染，根据这个结果，是否可以推断该次流感的感染率高于20%？”。通过前面部分的学习不难得出，该样本服从二项分布X～B(30，0.2)，依据题目背景，我们应当考虑到假设该流感的感染率为20%，假设X=20在n=30，p=0.2的二项分布总体中落在右尾的小概率区间，则说明该次流感的感染率高于20%；反之，如果X=20该事件没有落在n=30，p=0.2的二项分布总体的右尾5%的概率区间，则认为X=20是n=30，p=0.2的二项分布总体的正常值。思考至此，利用SPSS的累积分布函数CDF.BINOM计算出P(X≤19)的值为0.99，那么P(X≥20)=1-0.99=0.01，在显著性水平0.05下，P<α，那么X=20就落在了n=30，p=0.2的二项分布总体的右尾5%的小概率区间，认为该次流感的感染率高于20%。通过整个过程的学习与探究，我们不仅强化了二项分布的基础概念，并能运用概率计算解决推断问题，同时对假设检验推断思维的指导思想进行模拟训练。

3 方法与工具的简单程序化

随着教学进程的深入，我们开始了非参数检验中χ2检验的学习。由事例建立背景“某医生将两种药物在60名受试者的不同部位进行药敏试验，试验结果见下表。试问两种药物的药敏性是否有差异？(α=0.05)”。

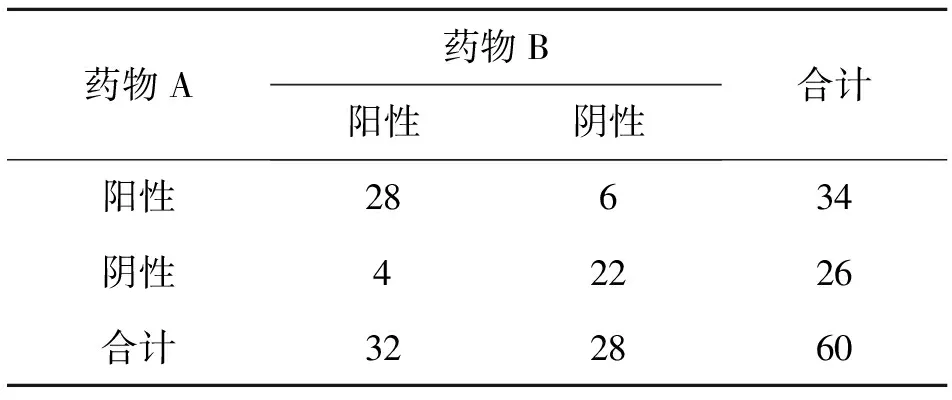
表1 药敏实验结果

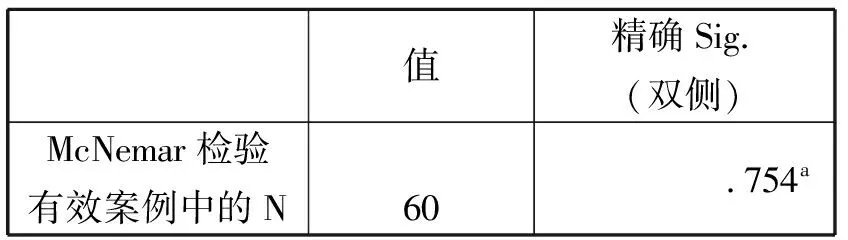
卡方检验

在建立常规假设检验的程序化方法的基础上，我们利用软件SPSS进行分析统计，首先建立数据集，利用描述统计中的列联表的McNemar统计工具，获得如图3所示的主要输出结果：

如图3所示，McNemar检验有效案例数为60，其概率P值(渐进Sig.(双侧))为P=0.754>0.05，故接受H0，认为“两种药物药敏性完全相同”。

在掌握χ2检验的程序化计算过程和简单化的SPSS软件操作后，老师让我们回归到二项分布的概率计算解答题目。推断Α、B药敏性是否存在本质差异的两个观察数值分别为4和6，即总例数为10(n=10)，两类数值差异若仅来自于实验误差，则各自分别占受试者总数的50%，即案例服从二项分布X～B(10，0.5)。利用SPSS累积分布函数CDF.BINOM计算得出P(X≤4)=0.37695，P(X≥6)=0.37695，P(X≤4)+P(X≥6)的双尾概率为0.7539，与McNemar输出概率一致，推断药物的药敏性差异由实验误差引起，无本质差异。

由上述思考分析过程，梳理整个知识体系，即利用二项分布基本方法，初探假设检验基本思想，理解??检验核心理论，将由二项分布引出的整个理论框架构建完整，为今后的内容复习以及其它相关学科的学习打下坚实的基础。这种发挥学生主体作用的教学方式，将传统的灌输封闭课堂转变为新型的对话开放课堂，在活泼有趣的课堂氛围下，把不被学生喜爱的“水课”转化为真正有温度、有深度、有难度的“金课”，极大地激发了学生的学习兴趣，为大学生培养自主学习能力与终身学习的观念注入强大动力。

4 以独立操作建立快乐学习

在老师引导下我们完成课程理论和实验学习后，下面就是我们自己利用所学把功夫用到刀刃上的时候了，利用2017级、2018级动物药学专业同学收集的个人身体指标做卡方检验的实操研究，以左臂高压数据进行总体率比较的R×C列联表来探究不同性别大学生的血压构成有无差异，具体实验操作过程如下。

第一步：查询相关文献报道，将大学生正常收缩压定义为100～130 mmHg，将205名同学分为高血压、正常、低血压三类，整理数据表如表2。

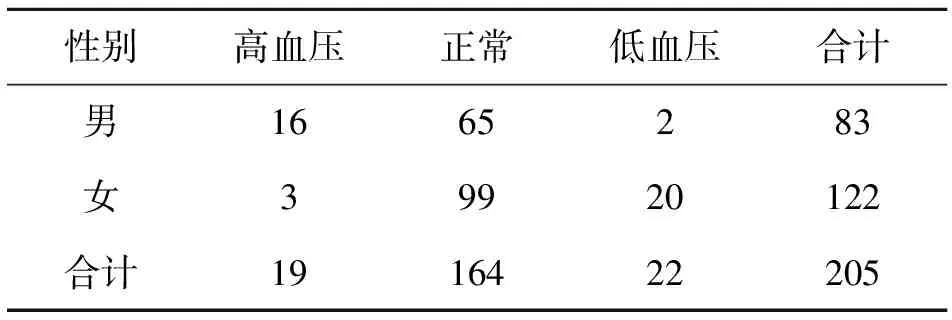
表2 205名同学左臂收缩压分布情况

应用SPSS建立数据集，并利用描述统计中交叉表，得到如图4所示的卡方检验输出结果。

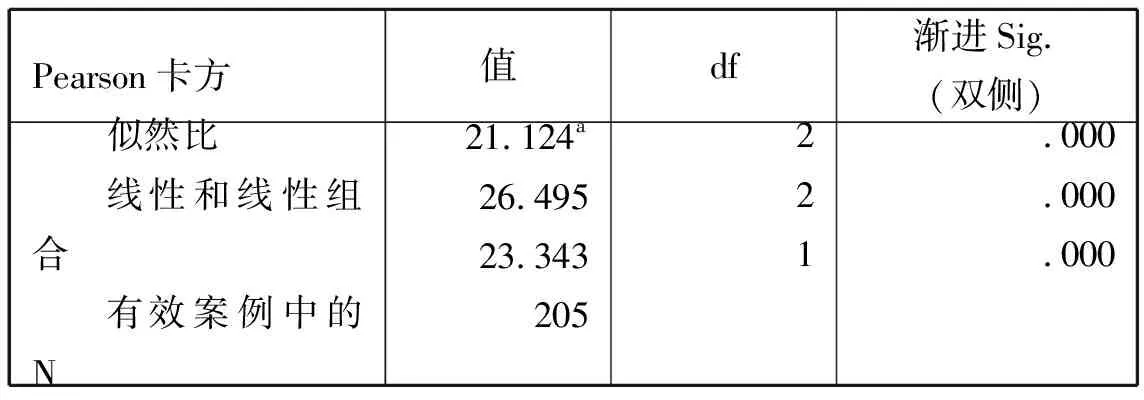
卡方检验

由输出结果可知，Pearson卡方值为24.124，概率P值(渐进Sig.(双侧))为0.000<0.05，故拒绝H0，即认为不同性别的大学生血压构成有本质差异。

由以上利用SPSS工具进行实际案例的分析，将所学课本知识真正运用到实处，不仅增添了自主学习过程的趣味性，也让我们更加深入理解本课程的教育意义，将专业课真正“学活”“学透”。认识到统计无处不在，不管是在学习和工作中，还是在生活中，都会用到统计，对客观存在的事物本质的认识和真相了解必须建立在以数据为依据的科学分析的基础上。由统计课程我们进行反思，对于我们大学生来说，我们应当主动积极从“单纯追究分数”转变到“自主求学探索”，这一转变不仅有利于我们培养自主学习能力和终身学习观念，也使我们更好的去理解学习的真正意义。