利用控制变量法解决复杂的质谱仪类问题

陈 喜

(浙江省诸暨市诸暨中学 311800)

随着国家新课程改革的推进，各地高考试题的问题情境都与生产生活、科技发展等紧密联系，同时也越加强调对学生应用物理学知识综合解决实际问题的能力.因此，质谱仪作为高中生学习的科学仪器之一，近几年频繁地出现在各地高考试题中，是高考考查的热点.

实际科学研究中，一束带电粒子的速度、加速电压、磁场磁感应强度等都可能在一定范围内取值，而且狭缝有一定宽度，粒子入射点位置也具有不确定性，另外粒子通过狭缝，由于波动性，其速度方向也在一定夹角范围内，因此粒子打在探测板上不是一个位置，而是在一段区域范围内，要区分不同比荷的粒子，必须使其击中探测板的范围不重叠.在高考试题命制时，命题者从实际问题出发，以质谱仪为任务情境，根据考查难度要求，对实际模型做适当的理想化处理，提出的物理问题往往分三个层次——理想化的质谱仪模型、单变量的临界问题、复杂的多变量的临界问题，从不同纬度考查学生应用物理学知识综合解决实际问题的能力.本文笔者从高考命题角度，总结解决质谱仪类问题的知识与方法.

一、掌握理想化的质谱仪模型的基本规律

理想化的质谱仪模型为粒子在加速电场中做加速直线运动模型和粒子在匀强磁场中的匀速圆周运动模型的组合.要解决这类问题，我们必须能运用动能定理处理粒子在加速电场中做加速直线运动问题，会运用向心力公式计算粒子在匀强磁场中做圆周运动的半径并规范、准确的作出粒子运动的轨迹图.

例1如图1所示，一个质量为m、电荷量为q的粒子，从容器下方的狭缝S1飘入电势差为U的加速电场，其初速度几乎为零，然后经过S3沿着与磁场垂直的方向进入磁感应强度为B的匀强磁场中，最后打到照相底片D上.

图1

(1)求粒子进入磁场时的速率.

(2)求粒子在磁场中运动的轨道半径.

(3)求粒子打在照相底片上的位置距S3的距离.

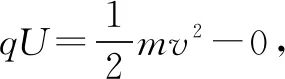
二、掌握动态圆的分析方法

实际问题中，由于粒子打在探测板上不是一个位置，而是在一段区域范围内，要区分不同比荷的粒子，必须使其击中探测板的范围不重叠.因此需要根据不同条件、情境分析粒子运动轨迹，求解击中探测板的临界情况.

1.利用放缩圆法分析粒子做圆周运动半径不同的临界问题

在质谱仪类问题中，若粒子的质量、电荷量、速度大小、加速电压和磁感应强度中某一个物理量的大小不确定，都会导致粒子在磁场中圆周运动的半径大小不同，此时我们应运用放缩圆分析由于半径不同而产生的临界问题.

变式1若匀强磁场的磁感应强度B取值在B0-ΔB≤B≤B0+ΔB范围内波动，求粒子打在照相底片上的位置距S3的距离范围.

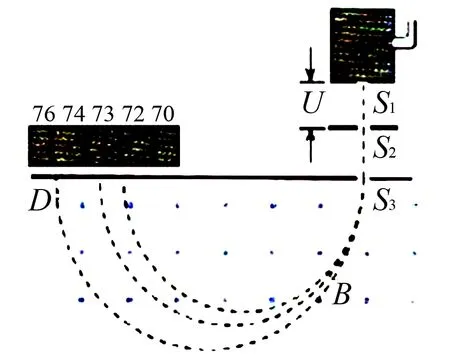
图2

2.利用平移圆分析粒子从不同位置进入磁场做圆周运动的临界问题

在质谱仪类问题中，若考虑狭缝宽度，粒子进入磁场的位置不同，进入磁场后的轨迹也不同，若各粒子进入磁场的速度方向都相同、圆周运动半径都相等，则各粒子的圆周运动轨迹经平移后可重合，此时我们应运用平移圆法分析此类临界问题.

变式2若狭缝S1、S2、S3的宽度都为d，求粒子打在照相底片上的位置距S3右边界的距离范围.

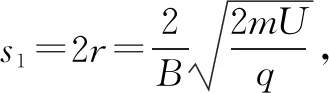
图3

3.利用转动圆法分析粒子以不同方向进入磁场做圆周运动的临界问题

在质谱仪类问题中，若各粒子从同一位置以不同速度方向进入磁场，做半径相同的圆周运动，则各粒子做圆周运动的轨迹绕入射点旋转可重合，此时我们应运用转动圆法分析此类临界问题.

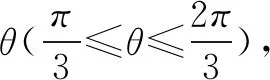
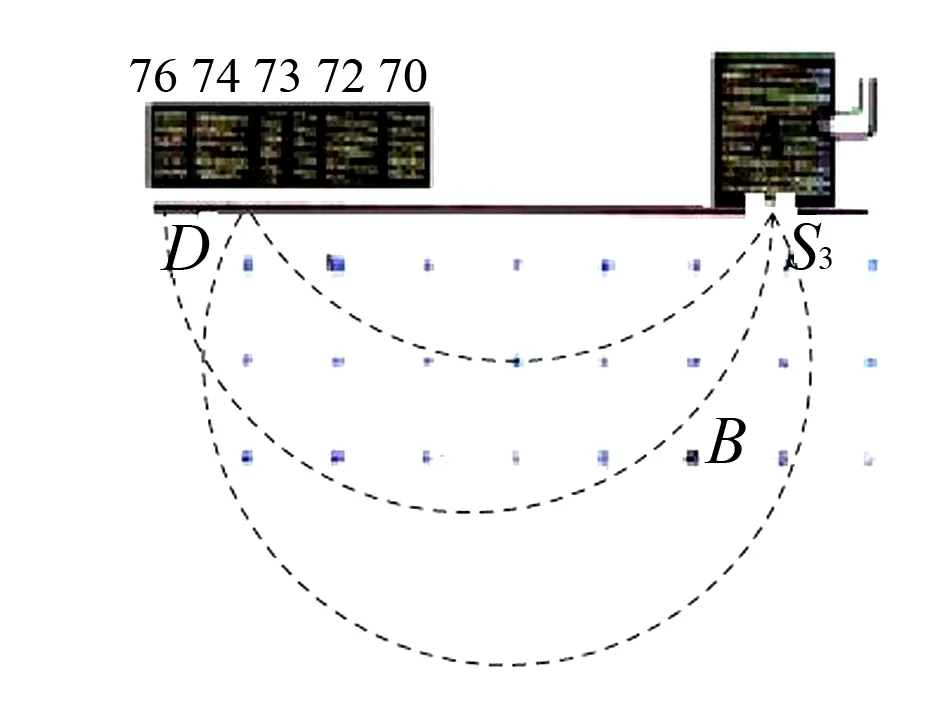
图4

三、利用控制变量法解决复杂的质谱仪类问题

在某些复杂的质谱仪类问题中，往往要求考虑两个或多个不确定因素，例如加速电压的取值在某范围内、狭缝也具有一定的宽度，更多的不确定因素会带来更多的粒子运动可能性，学生也更难确定这类问题的临界情况.笔者认为，对这类复杂的质谱仪类问题，可以运用控制变量法，降低思维难度，综合运用动态圆的分析方法，逐步总结推导出其临界情况.下面以此方法解答2017年江苏省高考物理压轴题第(3)问.

江苏2017(15).一台质谱仪的工作原理如图5所示.大量的甲、乙两种离子飘入电压为U0的加速电场，其初速度几乎为0，经过加速后，通过宽为L的狭缝MN沿着与磁场垂直的方向进入磁感应强度为B的匀强磁场中，最后打到照相底片上.已知甲、乙两种离子的电荷量均为+q，质量分别为2m和m，图中虚线为经过狭缝左、右边界M、N的甲种离子的运动轨迹.不考虑离子间的相互作用.

图5

(3)若考虑加速电压有波动，在(U0-ΔU)到(U0+ΔU)之间变化，要使甲、乙两种离子在底片上没有重叠，求狭缝宽度L满足的条件.

解析在本题中，甲、乙两种粒子的质量不同，电压为一范围值，入射点也不确定，使得本题求解的思维难度很大.下面我们利用控制变量法，逐步解决该问题.

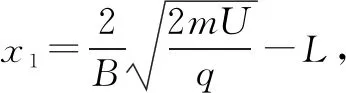
图6

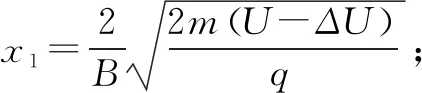
甲 乙

图8