双半圆柱平行电极系统的电场及其数值模拟

王福谦， 于学东

（四川西南航空职业学院机务学院，成都610400）

0 引 言

双半圆柱平行电极系统常用于二维电化学电池电流和电致化学发光强度等问题的研究［1-2］，但对该电极系统本身的电场分布的讨论，相关文献还未见报道。本文拟将保角变换、理论计算及计算机数值模拟相结合，研究双半圆柱平行电极系统的电场，给出其电势和场强分布函数，通过软件Matlab绘制其电场线和等势线图，计算其两极的最大场强，并分析其最大场强随电极参数的变化规律。

利用保角映射将具有复杂边界形状的区域映射为简单边界形状的区域［3-10］，将双半圆柱平行电极及边界所形成的复杂形状边界的区域变换为矩形域，则电极所形成的非均匀场就变换为均匀场，再将均匀场中得到的电势分布函数反变换至原求解区域，便可得到双半圆柱平行电极系统的电势分布函数，继而讨论该电极的场强分布函数。

1 电势分布与场强分布函数

有位于绝缘板上的两平行放置的半圆柱电极，其边界分别为Γ1和Γ2，半径分别为r1和r2，电极间距为g，左、右两电极的电势分别为-φ0和φ0，其横截面如图1所示。

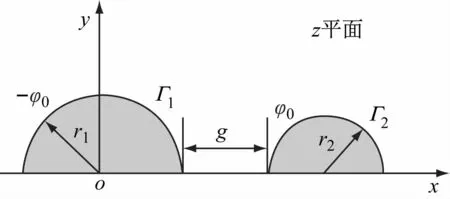
图1 双半圆柱平行电极的横截面

因在垂直于双半圆柱面母线的所有截面上的电场分布均相同，故本文所研究的电场为平行平面场。为方便地求出双半圆柱平行电极的电场分布，通过保角变换将双电极及边界所形成的复杂形状区域变换为矩形域［1］。通过分式变换函数

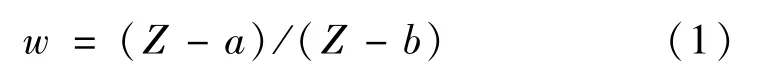
式中：

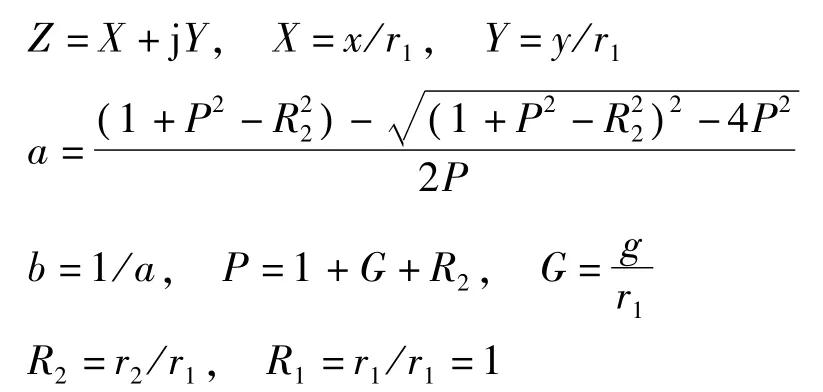
将图1所示的区域变换为半圆环形区域，如图2所示。再作如下的对数变换

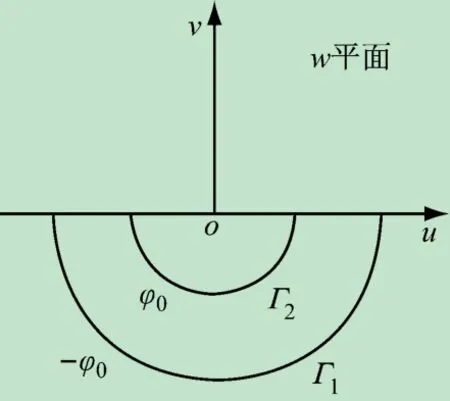
图2 保角变换后半圆环区域

将如图2所示的区域变换为矩形区域，且两半圆柱电极映射矩形的左右两个边，如图3所示。

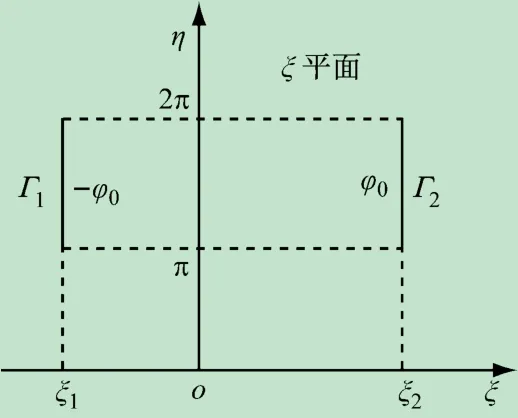
图3 变换后矩形区域

由变换式（1）、（2）可得

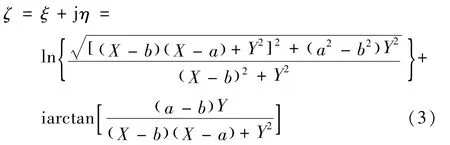
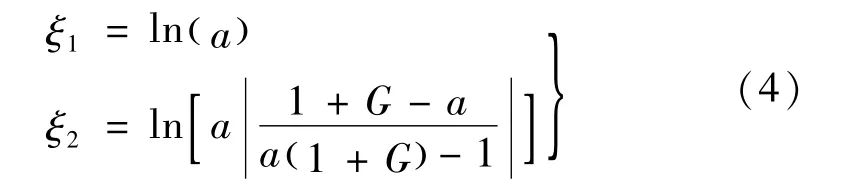
因在ζ平面上变换后的两电极之间的电场为均匀电场，则在该平面上两电极之间的电势分布为

将式（3）、（4）代入式（5），得

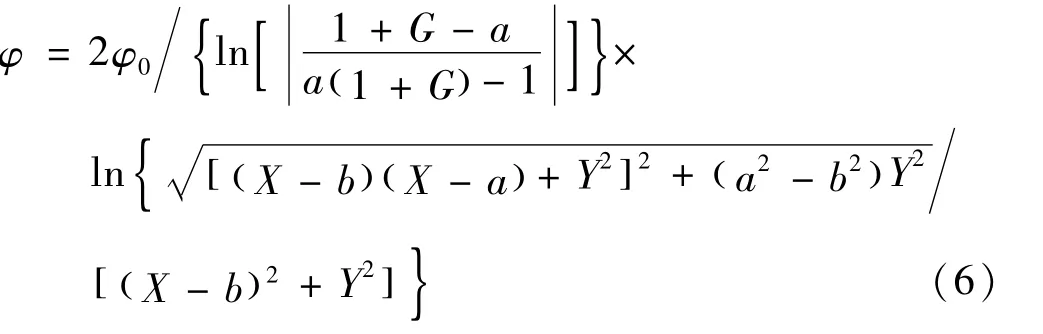
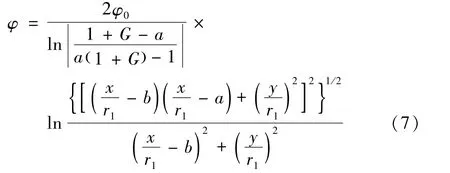
式（7）为双半圆柱平行电极所形成电场的电势函数表达式。 Δ

由场强与电势的微分关系E=-φ，利用式（7）可得

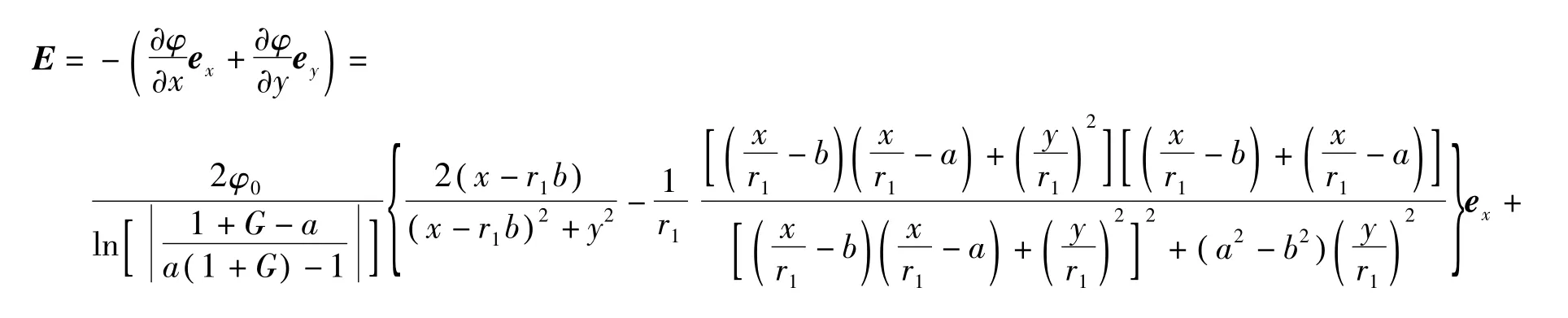
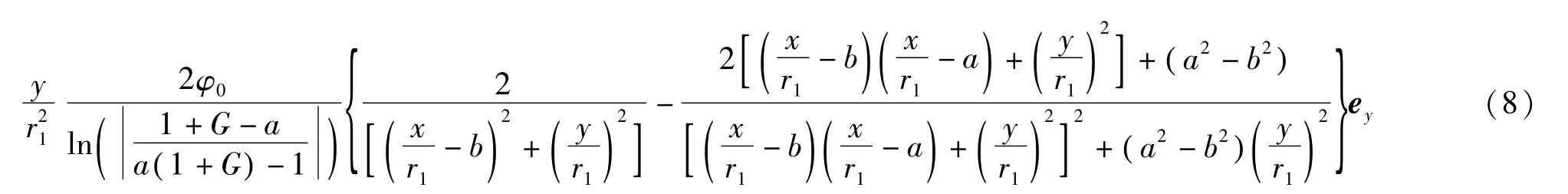
式（8）为双半圆柱平行电极电场的场强分布函数表达式。

2 场分布的数值模拟及电极形状蜕变的特殊情形的讨论

2.1 场分布的数值模拟

为给出双半圆柱平行电极的电场分布图的直观图像，以验证本文所得结论的正确性，下面用软件Matlab对该电场分布进行数值模拟，其三维电势分布图和横截面上的电场线和等势线的分布见图4、5（取U=100 V）。由图5可见：电场线与等势线及导体边界均垂直，场线分布正确，为预期结果。

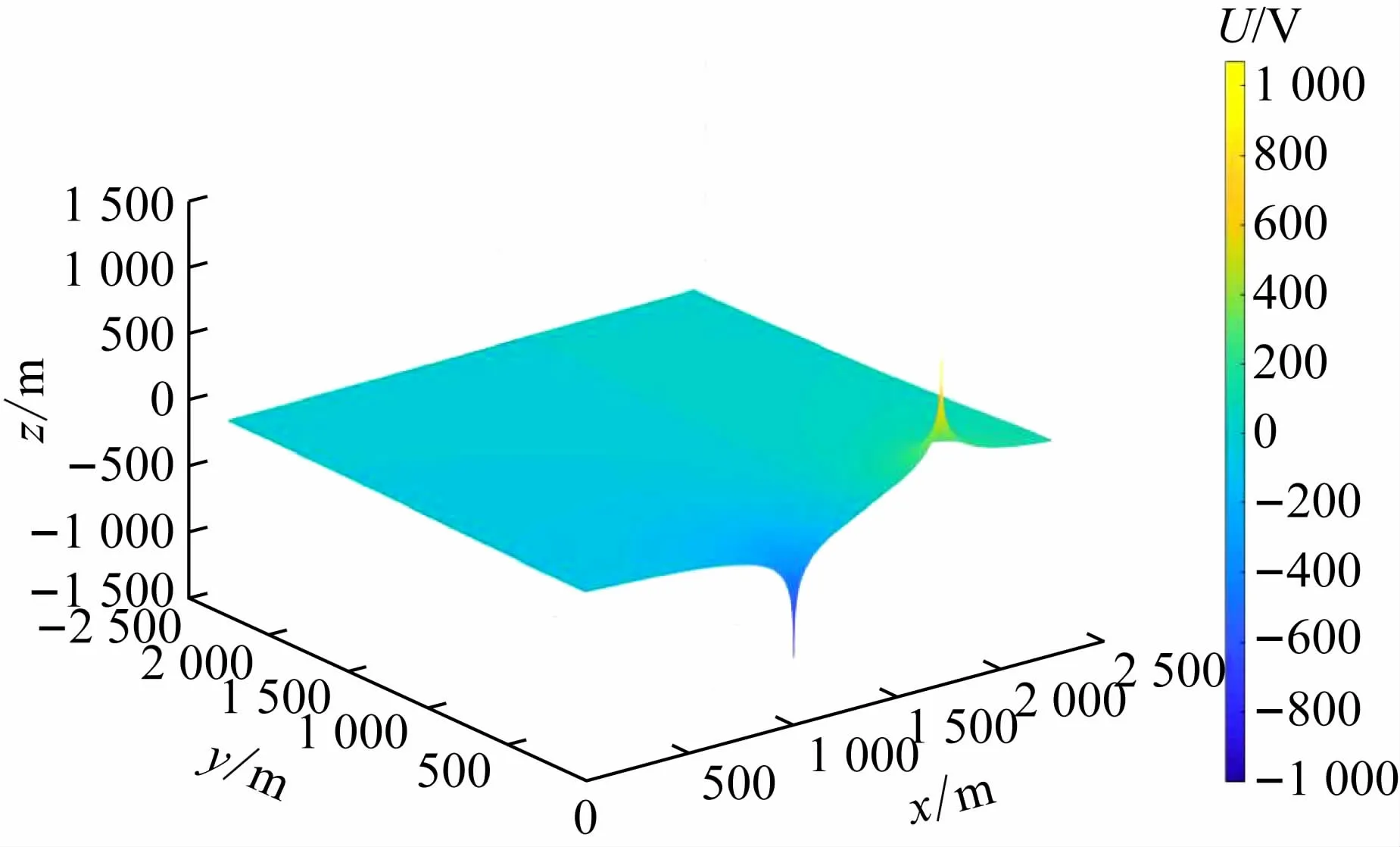
图4 双半圆柱平行电极的电场三维电势分布（r1=10 m，r2=8 m，g=5 m，U=100 V）

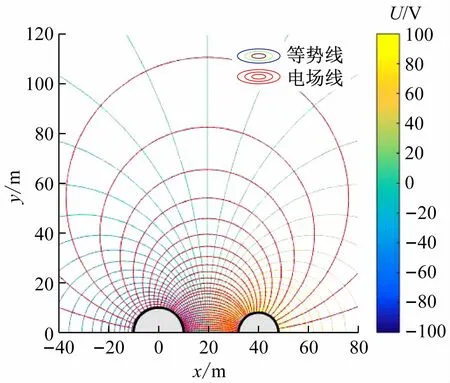
图5 双半圆柱平行电极的电场（r1=10 m，r2=8 m，g=20 m，U=100 V）

2.2 几种特殊情形的电场分布

当双半圆柱平行电极间的距离g=20 m，U=100 V，电极半径取一些特殊值时，可得到几种特殊情形下的电场分布，现讨论如下：

（1）当r1=r2=10 m时，此情形的电场为两半径相等的双半圆柱平行电极的电场（见图6）；

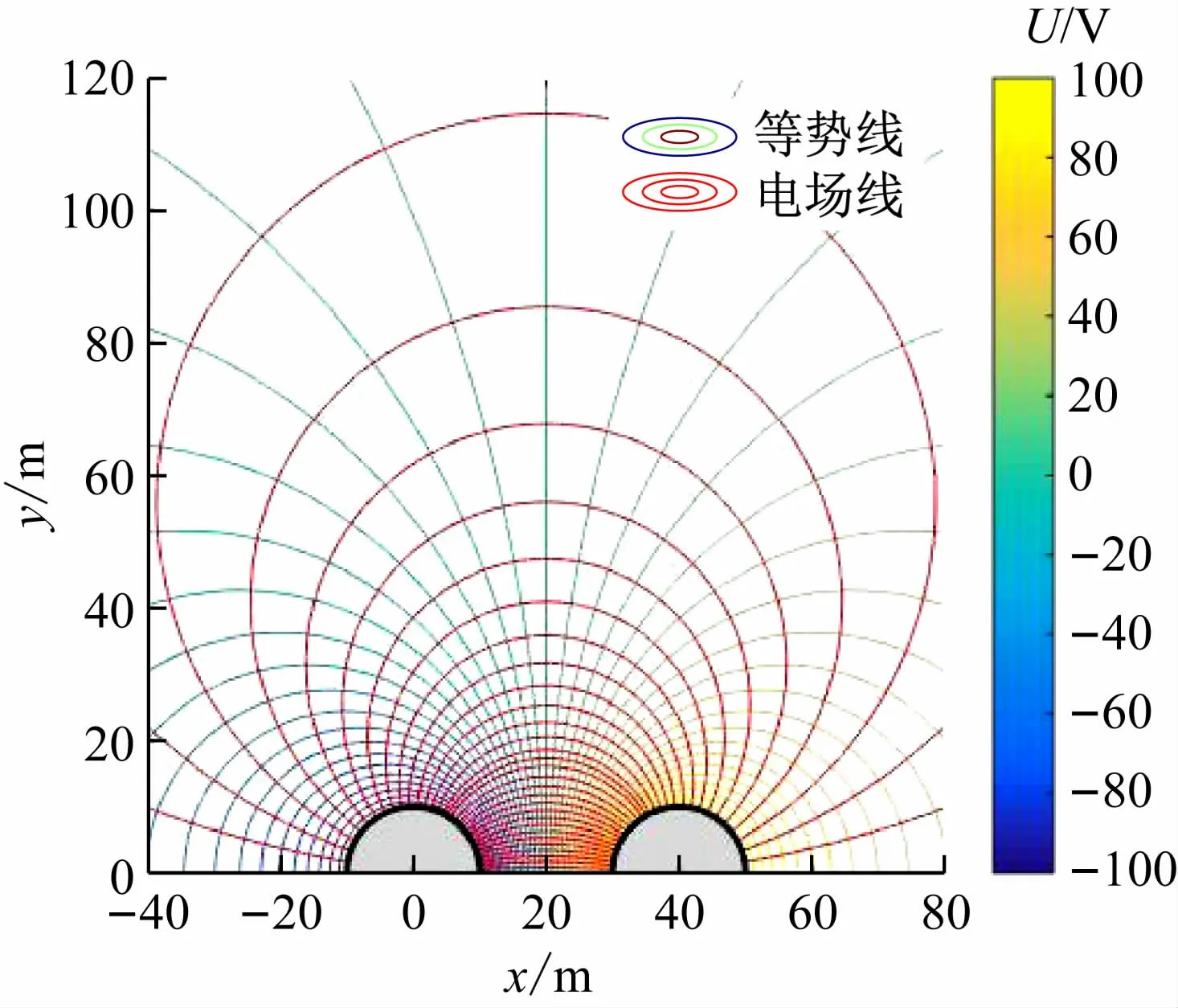
图6 等半径的双半圆柱平行电极的电场

（2）r1=10 m、r2=0.01 m时，此情形的可视为带电半圆柱荷和与之平行的线电荷所形成的电场（见图7）；

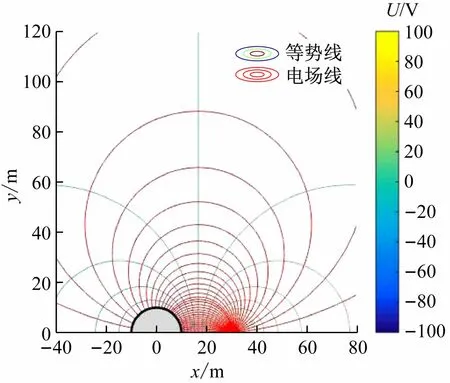
图7 半圆柱与平行线电荷所形成的电场

（3）当r1=r2=0.001 m时，此情形的电场可视为放置在绝缘平面上的两平行线电荷所形成的电场（见图8）。

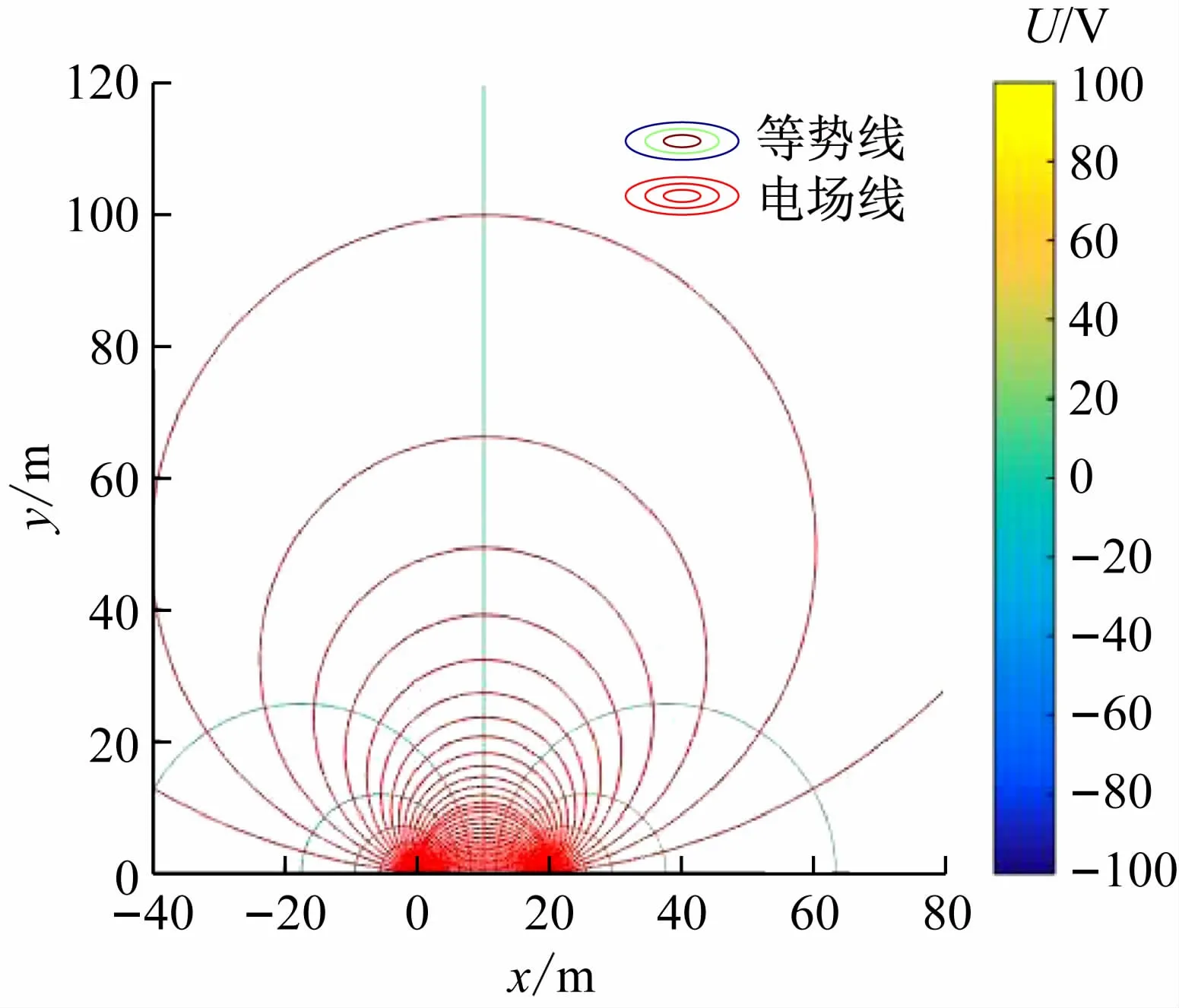
图8 置于绝缘平面上的平行线电荷所形成的电场

两半径相等的双半圆柱平行电极的电场、带电半圆柱荷和与之平行的线电荷所形成的电场及放置在绝缘平面上的两平行线电荷所形成的电场，均为本文所讨论问题的特例，本文的研究结论具有一定的普遍性。

3 电极电场的最大场强分析

3.1 电极电场的最大场强

双半圆柱平行电极底部边缘的曲率最大，再结合场分布模拟结果（见图5），知其场强最大处位于两半圆柱底部相对处的A、B两点，如图9所示。

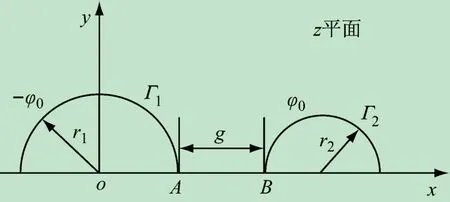
图9 双半圆柱平行电极的电场强度最大位置处A、B

对于电极Γ1右侧底部A处，有x=r1，y=0，由式（8），得

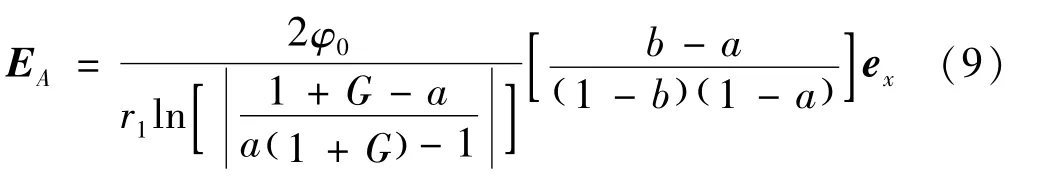
对于电极Γ2左侧底部B处，有x=r1+g，y=0，由式（8），得

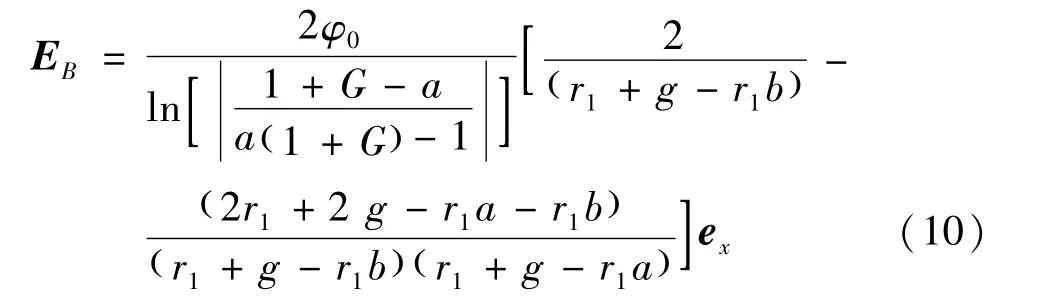
3.2 EA、EB随r1、g及r2变化变化规律

图10、11所示分别为用软件Matlab描绘出EA、EB随r1、g及r2变化的图像，实现了EA、EB随r1、g及r2变化规律的可视化。

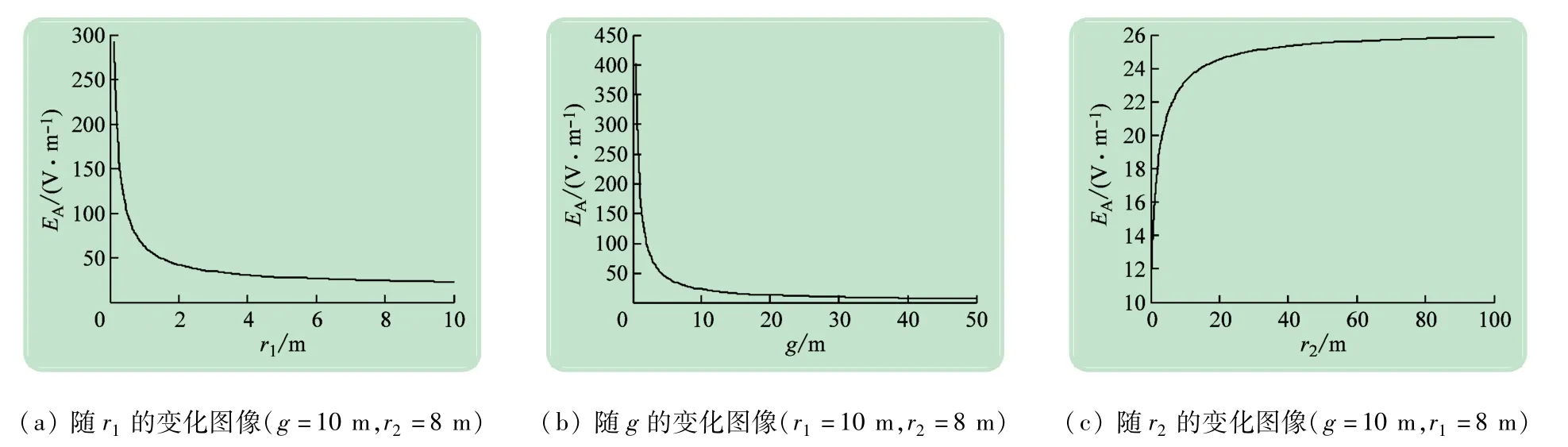
图10 E A随r1、g、r2的变化趋势

由图10可见，当g和r2保持不变时，随着r1的增大，电极A处的曲率边小，电荷面密度减小，其表面附近的场强EA也减小；由图11可见，当r1和r2保持不变时，随着g的增大，A处的电荷面密度减小，其表面附近的场强EA也减小；由图12可见，当r1和g保持不变时，随着r2的增大，A处的电荷面密度增大，其表面附近的场强也增大，且r2增至较大值时，EA随r2缓慢增加，并趋于一个确定值。由图13～15可见，EB随r1、g和r2的变换规律与EA相同。

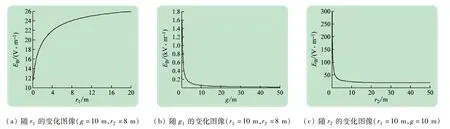
图11 EB随r1、g、r2的变化图像

4 结 语

本文将保角变换、理论计算及计算机数值模拟相结合，研究了双半圆柱平行电极系统的电场，得到了其电势分布和场强分布函数，并利用Matlab软件对场分布进行了数值模拟，给出了场分布的直观图像，为边界形状复杂的电极的电场分布问题的求解提供了一种新的方法，在科研上具有一定的理论意义和实用价值。