WUST10催化下废轮胎热解反应动力学分析
覃刘平,王 黎
(武汉科技大学 资源与环境工程学院环境污染绿色控制与修复技术研究中心,湖北 武汉 430081)
废轮胎很难进行物理、化学和生物降解,如果不进行适当处理,可在环境中存在长达100 a[1]。用热解的方法对废轮胎进行资源化利用有着不错的效果。随着热解反应的不断进行,废轮胎原料的理化性质发生改变,对其理化性质的变化趋势进行研究,可以了解轮胎的热解过程,为轮胎热解技术提供理论依据。废轮胎的热解属于多阶段复杂的固体热解反应。SU等[2]在对轮胎废物的热重数据进行动力学分析时采用的方法是假定轮胎热解反应为一级反应,但实际上轮胎的热解过程十分复杂,还伴随大量的中间反应。因此,在对废轮胎热解的动力学研究中仅用简单的反应机理构建模型并不精确,在实际建模中应考虑更多常见的反应模型和固态物质热解的相应机理。
本工作采用热重分析和差热分析(TGA/DTG和DTA)研究了废轮胎胎面颗粒在不同加热速率下热解过程的动力学和热力学,建立了废轮胎催化热解模型并求解了动力学参数和方程。分别考虑了废轮胎发生分子链解聚的吸热反应和只发生分子链断裂的放热反应,分析了废轮胎颗粒在不同加热速率下热解过程中吸热阶段和放热阶段的反应特性。以期指导热解技术在废轮胎回收利用中的应用设计和工程实践,实现节能。
1 实验部分
1.1 原料
实验所用废轮胎取自武汉天宇废旧轮胎回收利用中心,将其胎面通过机械化预处理粉碎成150目(约100 μm)大小的颗粒。采用德国Elementar公司Vario EL Ⅲ元素分析仪对其元素组成进行检测,具体结果见表1。

表1 废轮胎的元素组成和成分分析 w,%
1.2 催化剂
实验所用催化剂为本课题组自制:对商用的ZSM-5裂解催化剂(山东和发公司)采用两次交换加焙烧的方式进行氧化钇(Y2O3)改性,得到粉末状的Y2O3-ZSM-5;然后将Y2O3-ZSM-5粉体与无机黏结剂、无机纤维、有机塑形剂、造孔剂、水等混合均匀得到糊状物,用超声波去除其中的气泡;再经3D打印成型、表面功能化和高温焙烧活化后,即得到3D打印整体式Y2O3-ZSM-5催化剂块体(WUST10)。WUST10的比表面积为341 m2/g,平均孔径为3.21 μm,其照片见图1。

图1 催化剂WUST10的照片
1.3 热解装置和流程
热解装置如图2所示,为自制程序式升温的热解炉,加热最高温度为750 ℃。使用氮气为实验提供惰性环境,并将其流量设定为0.2 L/min,废轮胎样品质量为10 g,热解终温设定为600 ℃,加热速率分别设定为2,5,10,20 ℃/min。具体步骤如下:打开仪器电源,预热30 min;打开电脑并开启热分析,然后开循环水;取出坩埚,装入实验样品后放入设备内,关闭炉门;通入氮气,设定流量为0.2 L/min,使炉中的空气排空;热解结束后待炉膛完全冷却,取出样品,整理数据。

图2 热解装置照片
采用德国Netzsch公司STA 449型热重分析仪进行TGA/DTG和DTA分析。
2 结果与讨论
2.1 废轮胎热解动力学模型的建立
基于MARTÍNEZ等[3]的轮胎热解机理,优化建立了1个3阶段的废轮胎热解框架。在该框架中,第1阶段(P1):废轮胎中的有机添加剂经历反应过程P1直接热解生成了部分挥发性物质和焦炭,出现第1个明显的失重阶段。第2阶段(P2):废轮胎内的橡胶随着温度的提升发生主链断裂产生了热解的中间产物A。第3阶段(P3):中间产物A可被进一步解聚(P3a)形成挥发性物质和焦炭;或者直接裂解(P3b)形成短链有机中间产物B;中间产物B将最终热解(P3c)形成挥发物和焦炭。
上述热解框架中:反应P1,P3a,P3c属于质量损失反应,热解中会发生失重,属于吸热反应阶段;反应P2和P3c只发生了分子链的断裂解聚,属于放热反应阶段。本实验通过热重实验的结果拟合来检查框架是否正确。
2.2 吸热阶段的热解动力学
基于Arrhenius公式和LIU等[4]的热解质量损失计算模型,利用总质量损失是单个质量损失反应所造成的质量损失的总和进行计算。对于吸热反应P1,P3a,P3c,它们会发生质量损失,其热解动力学可用以下微分方程表示:
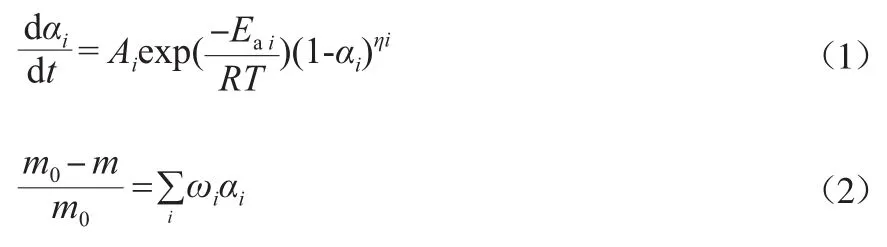
式中:αi为t时刻反应i的质量损失转化率,%;t为反应时间,s;ωi为反应i引起的质量损失贡献系数;m0为初始废轮胎颗粒的质量,g;m为t时刻废轮胎颗粒的质量,g;Ai为反应i的指前因子,s-1;Eai为反应i的活化能,J/mol;ηi为反应i的反应级数;R为气体常数,J/(mol·K);T为热力学温度,K。由于TGA/DTG分析是根据温度的变化记录质量损失,需将式(1)的时间变化改为温度变化来拟合实验数据,结果见式(3)。
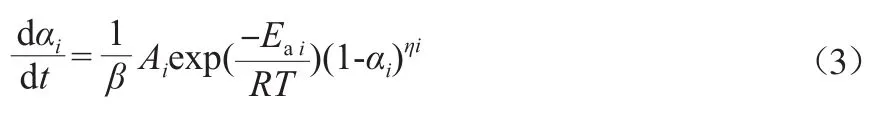
式中,β为反应的加热速率,K/s。
通过将此数学模型与TGA/DTG实验结果进行拟合,得到动力学参数(Ai,Eai,ηi)和质量损失贡献系数(ωi)。研究认为,加热速率影响的是每个吸热反应在整个热解中的质量损失比例,对动力学参数并不会产生影响[5]。对于吸热反应P3a和P3c,只考虑质量损失贡献比例会更明确,也更方便计算。因此,本实验可以认为对于不同加热速率下的热重实验,动力学参数Ai,Eai,ηi和ω1是相同的,只有反应P3a和P3c的质量损失贡献系数(ω3a,ω3c)因加热速率而变化。然后采用最小二乘法对不同加热速率下的实验数据进行曲线拟合,并用欧拉法来求解模型内部的微分方程[6]。
利用Flynn-Wall-Ozawa法[7],得到反应模型的积分形式g(αi):
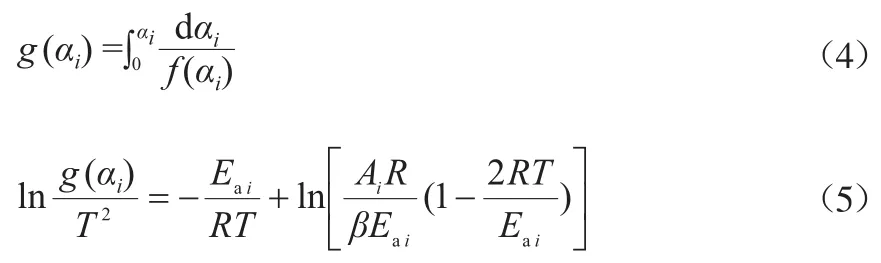
采用Malek法[8]选出f(αi)(反应机理函数,(1-αi)ηi)中最合适的反应级数ηi,使线性回归方程具有较好的相关系数。经多次拟合计算,P1,P3a,P3c的反应级数ηi确定为2.24,0.95,0.89,从而得到f(αi)。ln[(AiR/βEai)(1-2RT/Eai)]的值可以近似看做一个常数[7],进而用得到的f(αi)可确定g(αi)。
确定吸热反应的动力学参数时,根据ln[g(αi)]/T2与1/T呈线性相关,做出直线,求得反应的活化能Eai和反应的指前因子Ai。采用最小二乘法使每个质量损失反应的优化目标函数(Si,见式(6))最小。然后对3个质量损失反应的损失进行合并,通过每个损失的贡献率进行各项的加权,让模型和实验结果值更为相近[9]。

式中,αic为αi的实验值。
综上,得到P1,P3a,P3c的动力学线性回归方程分别为:y=-8 307.3x-1.624 0,y=-14 067.8x+1.214 9,y=-15 507.2+1.733 0,其相关系数分别为0.996,0.995,0.998。3个吸热过程的动力学参数见表2,根据最小二乘法得到的每个反应过程对应的质量损失的贡献系数见表3。

表2 吸热反应的动力学参数
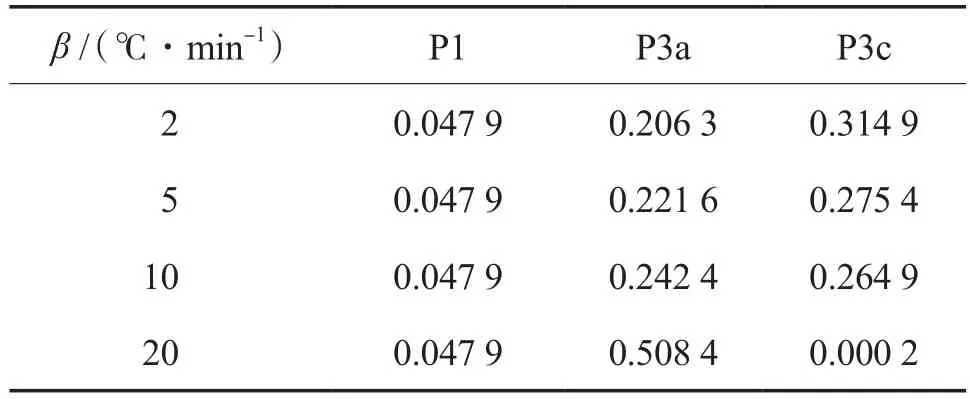
表3 吸热反应的质量损失贡献系数(ωi)
从表3可以看出:随着加热速率的增大,P3a的质量损失贡献系数增大,而P3c的贡献系数降低;当加热速率从10 ℃/min增至20 ℃/min时,这种变化最为明显;在本实验的加热速率范围内,ω3a增加了1倍以上,ω3c减小到几乎为0。对于较高的加热速率,热解系统会较早地达到高温,这为废轮胎提供了足够的能量分解成较短的分子产物,即挥发物和焦炭。在所提出的动力学框架中,这一过程由P2和P3a表示。因此,ω3a会随着加热速率的增大而增大。另一方面,随着加热速率的升高,大部分废轮胎颗粒已经通过P3a热解成挥发物和焦炭,中间体A经历的P3b和P3c的部分就不可避免地减少了。因此,当加热速率增大时会使ω3c减小。
利用上述模型对热重曲线进行拟合,结果见图3。可以看出:随着加热速率的升高,废轮胎的热解速率加快;实验值和拟合曲线吻合程度很高,具有不错的拟合效果。这也进一步证明了废轮胎热解模型的正确性。
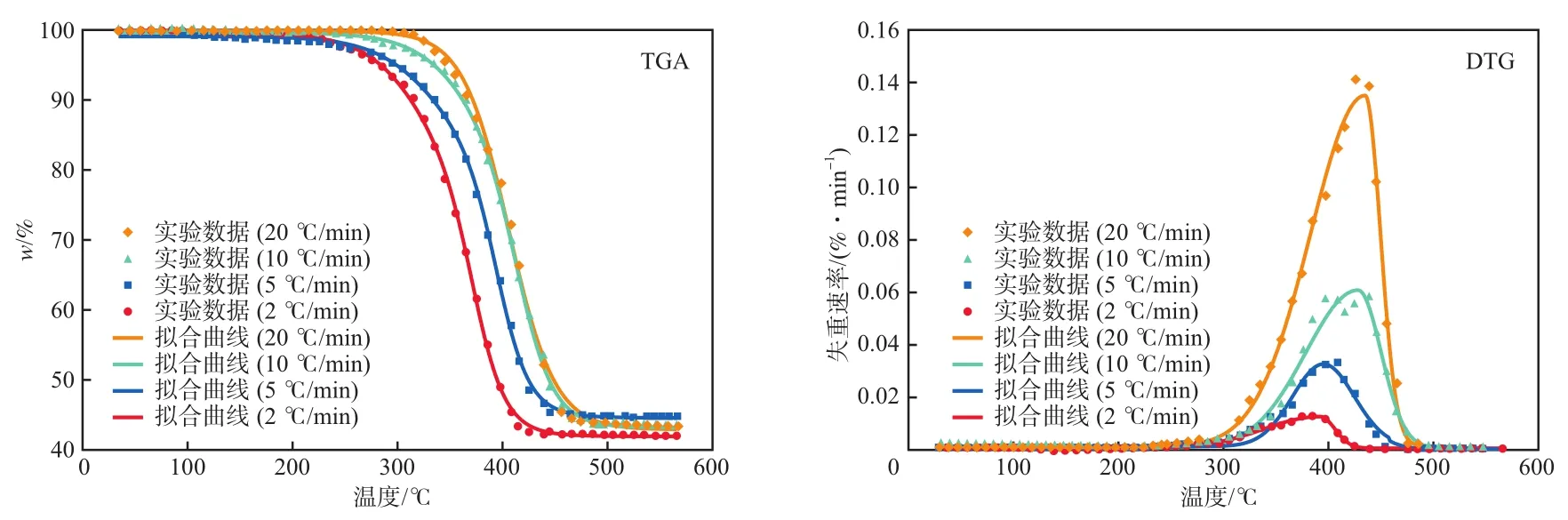
图3 不同加热速率下TGA/DTG的实验和拟合结果
2.3 放热阶段的热解动力学
在P2和P3b中,有机物主要被分解成较短的分子链,这个过程通常是放热的[10]。该过程中没有质量损失,因此放热动力学只能通过热解废轮胎内部的热量来分析。热量计算涉及了废轮胎的比定压热容、放热反应热容和汽化热。与质量损失反应不同,P2和P3b应满足如下方程[11]。

式中:γj为t时刻放热反应j的热解转化率,%;Aj为放热反应j的指前因子,s-1;Eaj为放热反应j的活化能,J/mol;ηj为放热反应j的反应级数。
根据热力学定律,废轮胎样品内部的热量变化(ΔQ,J)应为显热、潜热、反应热、热损失之和。基于HAMEED等[12]的方法,假设热损失可以忽略不计,其他热量可用如下的热力学关系式计算。
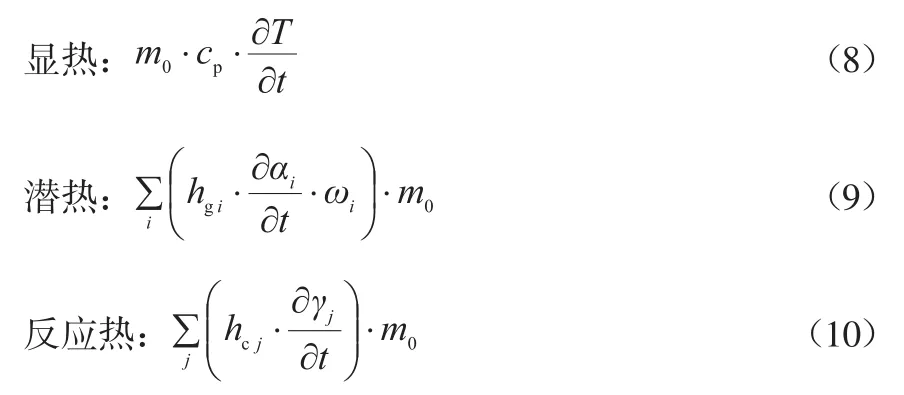
式中:cp为比定压热容,J/(g·K);hcj为放热反应j的反应热容,J/g;hgi为反应i的汽化热,J/g。通过DTA数据拟合选择合适的参数(Aj,Eaj,ηj,hcj和hgi),使用最小二乘法将ΔQ的实验值与拟合值之间的误差最小化[13]。得到的放热反应动力学参数值列于表4。

表4 放热反应的动力学参数
2.4 全过程热解动力学拟合
废轮胎热解中吸热反应所需的能量与焓变大于放热反应释放的能量,这使得热解成为一个整体吸热过程[14]。采用热重分析仪对废轮胎样品颗粒进行DTA,用所得数据进行拟合得到热力学参数(焓变),详见表5。由表5可知,在不同的加热速率下,放热反应的热量在发生变化。实际上反应热反映的是反应物和产物之间的焓变,这些放热反应的反应物是相同的,放热的变化也就应该是不同加热速率下的不同产物造成的。
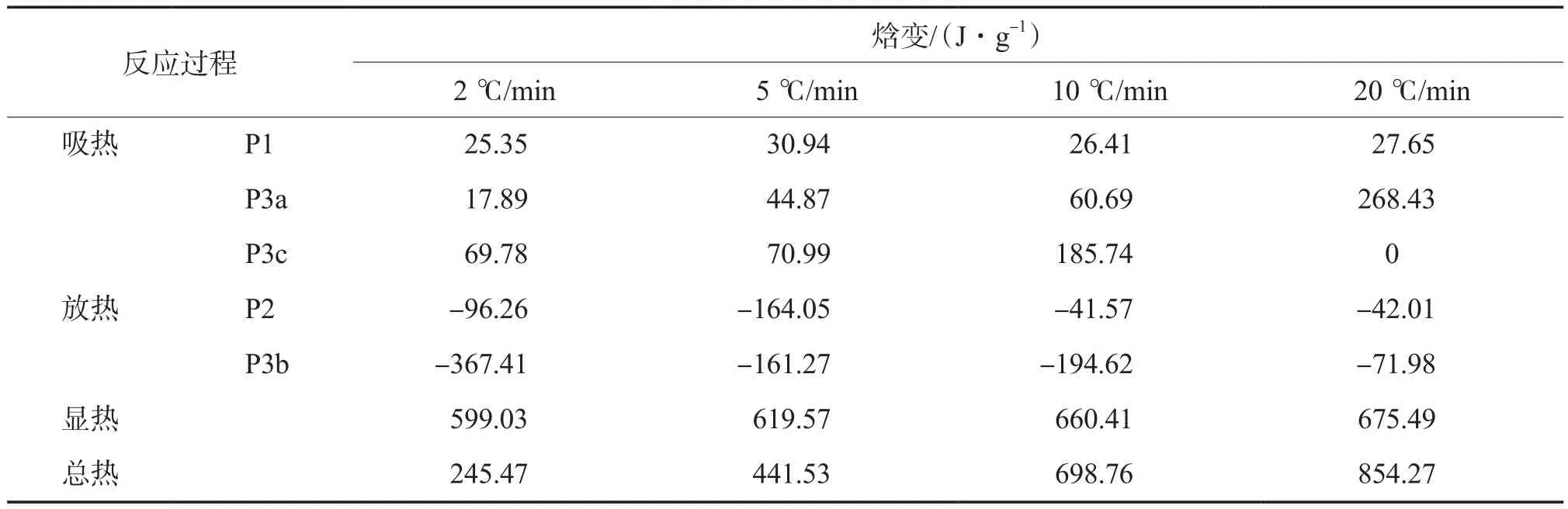
表5 不同加热速率下焓变的拟合结果
不同加热速率下DTA的实验和拟合结果见图4。图4所示的正峰代表热解期间发生的放热峰。可以发现放热峰出现在200~400 ℃之间,且位于两吸热峰之间。这十分符合本实验的热力学框架。图4还说明了吸热反应的性质。其中,发生有机添加剂被热解和汽化的过程P1产生了第一吸热(负)峰。可以发现在不同的加热速率下,第一个吸热峰的大小是相近的。这表明反应P1的确与加热速率无关,它恰好匹配了ω1不变的论点,与前文所述一致。对于另外两个质量损失反应P3a和P3c,它们在图4中形成1个综合的吸热峰。注意到它们在更高的加热速率下吸热变得更强,这与不同升温速率下热解产物的变化有关。
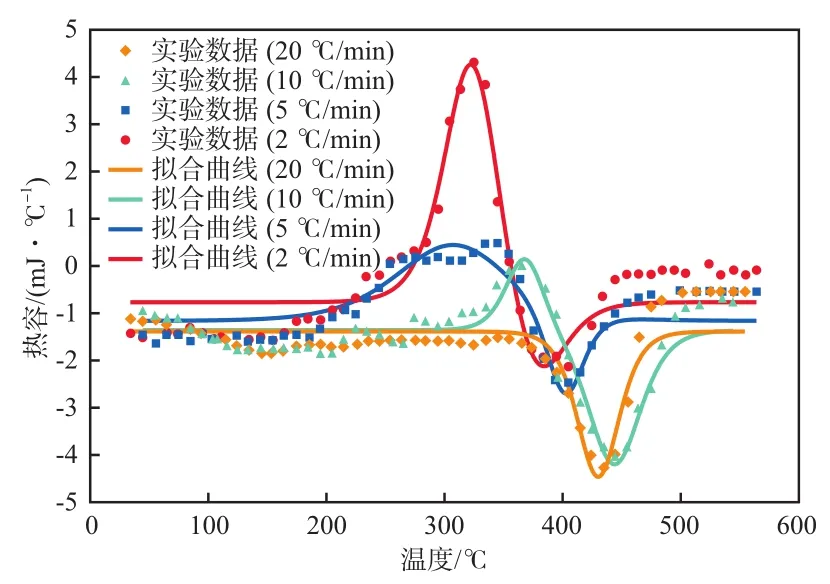
图4 在不同加热速率下DTA的实验和拟合结果
WILLIAMS[15]研究发现,当加热速率升高时,不凝气体的收率增加,热解油的平均分子量降低,产物蒸发需要更多的能量,因此,更高的加热速率下质量损失反应的吸热更多。这与我们的实验结果和拟合回归也是一致的。同时,在实际应用中,更高的加热速率下,蒸发的热量比放热反应热量大得多[12],热解总体上会吸热更多。基于以上的讨论和分析可以发现,本实验优化的综合模型与实验数据有良好的拟合关系。由图5可以看出,大多数实验点处于拟合回归线上,但有些部分的拟合效果并不十分理想。这可能是由于没有考虑废轮胎颗粒内部的热传递效应,未来可以从颗粒内部传热过程方面对模型进行优化。
3 结论
a)建立并优化了废轮胎颗粒的催化热解框架,主要包含3个发生质量损失的吸热反应和2个仅发生分子链断裂不会产生质量损失的放热反应。
b)3个吸热反应最合适的反应级数分别为2.24,0.95,0.89。其线性回归的相关性系数均在0.99以上。计算得到了不同加热速率下废轮胎热解反应5个过程的动力学参数。
c)DTA曲线中,有机添加剂被热解和汽化会产生第一吸热(负)峰。第一吸热峰的大小与加热速率无关。热解的后半程形成1个综合的吸热峰,更高的加热速率下会形成更高的吸热峰。DTA曲线中,放热反应的放热峰出现在200~400 ℃,位于两个吸热峰之间。本实验优化的综合模型与实验数据有着良好的拟合关系。
d)放热反应的热量在不同的加热速率下会发生变化。随着加热速率的升高,废轮胎的热解速率加快,热解系统会较早地达到高温,为废轮胎提供了足够的能量来快速分解成较短的分子产物(挥发物和焦炭)。在实际的热解过程中,可以通过对热解加热速率的改变对相应产物进行选择。

