模拟退火算法求解排队中的加急问题

邓梦怡，吴旺春，胡春筠，俞龙，胡菁

（华南农业大学电子信息工程与人工智能学院，广州5106401）

1 综述

1.1 问题的研究背景

近年来快递市场的竞争日益激烈，越来越多的快递企业为了缩短交货期，开始开发更快捷的服务，如“次日交货”、“次日早晨交货”[1]。因此，快递企业要想在快递市场赢得更多的客户，就必须形成核心竞争力。快递中转站作为物流行业的一个重要节点，每时每刻需要面对无限的快件数，快件流量大，随机性强，工作情况变化快。因此，如何及时、高效、准确地将快递运送至顾客手中，这对于获取消费者的好评、延续与商家的合作至关重要。

1.2 问题来源

快递中转站如若无法及时合理地处理快件，就会导致工作效率低，许多快件也会无法按时发出。而快递中转站中机器调度可能受到机器类型、工作特点、机器成本等诸多因素的制约。由于不同类型的快件处理所规定的时间不同，且快件到达数随机性强[2]，因此，机器调度问题并非简单的线性规划问题，机器处理方案导致的时间冲突也成为机器调度中的关键问题。针对排队问题，许多研究者做了大量的研究，目前有遗传算法、禁忌搜索等优化算法，将排队问题简化为单目标规划问题迭代求解，但《随机排队论对大型医院急诊观察室工作流程的优化》[4]、《航班登机口分配问题的数学建模》[8]等文献中提到的研究方法适于解决单位时间流量较少且队长较稳定情况下的问题，但由于快件具有随机性强、流量大等特点，若将同样的方法应用在快件问题上，求解出的等待时间波动大且不稳定，这不利于机器及时识别快件类型并及时做出调度，从而加剧了机器的阻塞。

1.3 基于不同快件类型的排队问题研究模型

本文在随机排队论的基础上对排队问题加以完善，以时间为约束条件进行多目标规划，并引入优先级的概念，将加急快件与普通快件设置为不同的优先级，通过模拟退火算法进行迭代计算。在时间不冲突的条件下，综合优化机器的分配方案，适当地延长普通快件的平均等待时间，提高加急快件优先级，根据实时机器工作特点以及快件量做出响应的调整，从而完善快件的处理方法、获取消费者以及商家对物流服务的满意度[3]。

2 问题的描述与假设

为优化快件的处理，可以将快件处理问题理解为先来先处理的排队问题，通过对快递中转站每日到达快件数进行分析，在快件量基本为饱和状态的情况下，安排机器的工作休息时间。快递中转站机器调度是指在考虑快件等待时间、机器工作特点、规定截止工作时间等因素的情况下对某个时间段内到达的快件分配合适的机器。本文结合随机排队论分析等待时间，寻求缩短加急快件等待时间的方法；结合约束条件，快件流量最大化进行多目标分析如图1所示。根据快件处理的不同需求，本文设置不同的权重系数，将多目标转化为单目标[5]，运用模拟退火算法求解。

图1 多目标分析

3 模型的建立

普通快件与加急快件处理时间范围不同，在机器被全部使用的情况下，快件只能等待，可能对物流的速度带来不利影响。因此，快件与机器的调度应首先把机器尽可能多地分配到加急快件中确保快件按时发出，实际数据处理过程中，我们应根据快件的性质合理地设置排队序列，具体流程如图2所示[5]。

图2 快件处理流程

3.1 排队序列的设置

生成1到n之间的随机整数序列（代表n台机器），以先到先服务的原则对快件随机地进行机器分配。为体现分配情况，将一天化为86400秒，产生n×86400的全零矩阵，代表每件快件可分配秒数，若快件成功分配则对应机器秒数记1，否则记0[6]，即若机器与快件处理时间冲突，该时刻机器记0，返回上一层；若不冲突，则分配至此[7-8]。

3.2 随机排队论

中转站对快件的处理是一个典型的M/（M×N×∞）排队等待服务问题，单位时间内所需生产加工处理的普通快件数符合到达率为λ的泊松分布[9]，其中紧急快件等待时间要尽可能地缩短才能满足需求。因此，引入具有优先级的排队分析，设置普通产品优先级较低，服从到达率λ1泊松分布；加急产品优先级高，服从到达率λ2泊松分布[10]。令单位时间机器处理快件能力为μ件/小时，则单件产品处理时间T为1/μ，相关性能指标如表1所示[11-12]。

表1 相关性能指标

根据加急快件的比例，除以一个趋近1的数，可以适当延长普通快件平均等待时间：

由于快件平均处理时间不变，根据各类快件比例，解出加急快件平均等待时间：

3.3 多目标规划

每台机器开始处理快件的时刻都是随机的、独立的，而且所有机器处理快件必须满足每天工作要求。考虑到在t时刻到达的普通快件须在t1时刻前完成，加急快件须在t2时刻前完成从而建立约束条件。针对表1的3个目标，为了保证机器的工作效率最大化，可建立以机器处理快件量最大化，且快件平均排队时间最短最小化的多目标规划模型[13]：

其中，zk为第k个目标，Cij为第i台机器在j时刻处理或生产的物品件数，xij为第i台机器在j时刻的工作状态，当机器处于工作状态时xij=1，当机器处于不工作状态时xij=0。

对机器处理快件量、快件平均排队时间、加急快件平均排队时间分别赋予加权系数a、b、c构建关于λ的单目标模型[14-15]：

3.4 模拟退火算法

单目标模型较难求解，因此考虑用模拟退火算法来解决快件处理问题，以便较好地处理复杂目标函数。算法通过a、b、c设置普通快件与加急快件的优先级后，根据适应值，判断是否接受新的处理方案进行对比计算，通过迭代进而求得最佳方案[16-20]。对目标函数进行求解方法如下：

（1）以最大快件量为初始解（设置退火温度）；

（2）结合优先级设惩罚系数，求解目标函数，计算目标值的变化量D，并与初始解比较；

（4）设置退火代数，如若达到，则视为最优解[21]；

（5）通过最优解结合加急快件占比求得相应的排队队长，更新排队序列。

3.5 算例分析

某快递站所有设备处理快件能力约为5600件/小时，72小时中快件平均到达件数为5560件/小时（部分时间段超出5600件/小时），加急快件约占快件的3.245%。本方案求解得出的各项指标如图3所示。

图3 各项指标

图3 在部分加急快件适当插队的情况下，由于加急快件的比例相对较低，加急快件对普通快件的排队等待时间影响有限，故普通快件平均等待时长仅增比1.65%，而加急快件等待时长却缩短了49.10%，效果较好，该方案可以大幅度地缩短加急快件处理时间，而普通快件的处理时间仅有小幅度的上升。为探究两类快件所受影响的程度，下面根据加急快件所占比例及其波动程度作进一步的探究，当平均所有快件到达率为5560件/小时，加急快件占比不同的情况下排队时间增减比例如图4、图5所示。

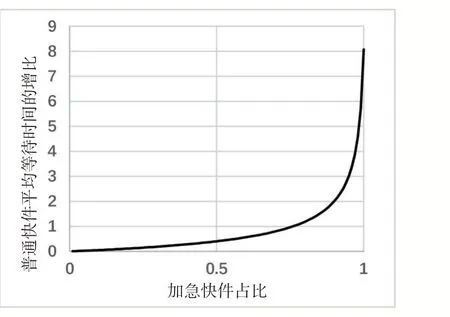
图4 普通快件所受影响

图5 加急快件所受影响

对比可知，随着加急快件比例的增大，优先级对加急快件的影响逐渐减弱直至消失。随机排队论对大多数比例的加急快件均表现出较好的效果，其中加急快件占比较小的情况下效果更佳。

模拟退火算法对目标规划中的式（7）求解，具体参数如下：迭代总数为1000，初始温度为5560℃，温度冷却系数为0.97，且结合实际，将式（7）中的权重系数a、b、c设为1、5、10，迭代次数与目标函数maxzz的关系如图6所示。

图6 迭代效果图

在权重系数a、b、c分别为1、5、10的情况下，当所有快件到达率为5410件/小时为图6中的拐点，经迭代计算得到的拐点处目标函数取得最大值、效率最高。

《随机排队论对大型医院急诊观察室工作流程的优化》[4]通过排队论求解排队时间再根据加急快件所占比例缩短加急快件的排队队长，其与本文提出的方案各项指标对比如图7、图8所示。

由图7、图8对比可知，对比方案中的两个指标在断点附近（快件到达率超出设备处理能力）排队时间大幅度增加、波动大；加急情况下求解出的加急快件的平均等待时间由76.2秒降至0.632秒可知其加急快件排队队长的设置是不合理的，这不利于机器及时识别快件类型做出机器的调度。而本文提出的方案通过式（1）以及目标规划设置优先级，用模拟退火算法得出最优解，从而使排队时间更加稳定波动减小，同时可通过调整优先级设置更为合理的加急快件队长。综上所述，本文提出的排队方案更加稳定，且更有利于机器及时识别快件种类并做出调度。

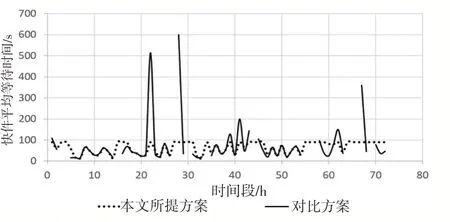
图7 快件平均排队时间对比

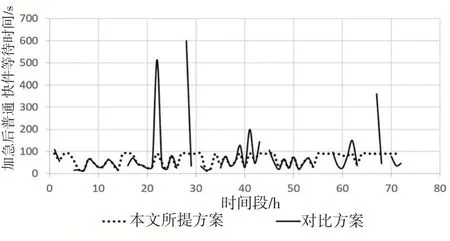
图8 加急后普通快件等待时间对比

4 结语

本文模型的建立考虑到机器工作特点、规定工作快件处理时间、快件加急情况等，通过随机排队论求解排队时间、设置优先级，确立多个目标函数，结合约束条件，设置优先级转化为单目标规划，最后使用模拟退火算法实现三个优化目标效率的优化并更新队列，其结果对机器的调度具有一定的参考价值。