吸入式喷嘴的风速标定装置的标定效果分析

陈栩颖

（上海海立电器有限公司，上海 201206）

0 引言

空气流速是一个常用的测试参数。制冷暖通领域很多电器的性能测试都会用到该参数，如房间空气调节器采用空气焓差法测试制冷量时用到了风量这个空气流速所对应计算值[1]。目前，空气流速点风速主要的测量装置是热线风速仪、毕托管等。而风速测量设备在使用前都需要对其进行标定。风速标定的目的是对各风速仪的性能进行测试。

目前行业中普遍采用的风速计标定方法有两种：一种是旋臂机法，此方法结构复杂，易扰动静止的空气，从而影响标定精度；另一种是相对标定法，此方法不易实现1.0 m/s 以下的低风速标定和校正，且毕托管本身标定也会带来一定的误差，另外，风速改变引起风管内速度场的不稳定也会对标定精度带来影响。因此，如何方便快捷实现风速计在低风速的标定与校正，同时保证标定的精确度和准确度，是测试领域需要解决的问题[2]。参考压差式风量测量的方法[3-8]，该测量的方法是通过改变风机频率大小，在风管中不同风速状态下进行风速测量和装置标定。该方法通常采用的装置为压差计和毕托管。如何保证测量的精确度和准确度是该测量方法的重要关注点。该方法在管内风速过大时，风速测量的误差会增大，所以一般的实验会控制风管内的风速在低速中进行。但风速进一步升高后，风管内风速以及标定的不确定度[9-13]研究较少。

本文研究了一种负压的通过空气流量转化为点风速的风速标定装置。并对该装置标定的结果进行不确定度的计算从而检验该装置标定的效果。

1 实验方法及原理

1.1 实验装置

在用于实验室测量风量的节流装置中，喷嘴是目前国际上公认的一种准确而方便的装置[14]，其流量系数稳定，相对同流量的其他节流装置，其阻力损失更小，因此越来越多应用在风量实验系统中。配合各种差压计或差压变送器可测量管道中各种流体的流量。

基于吸入式喷嘴的风速标定装置，即应用压差式风量测量原理进行设计，装置布置如图1所示。

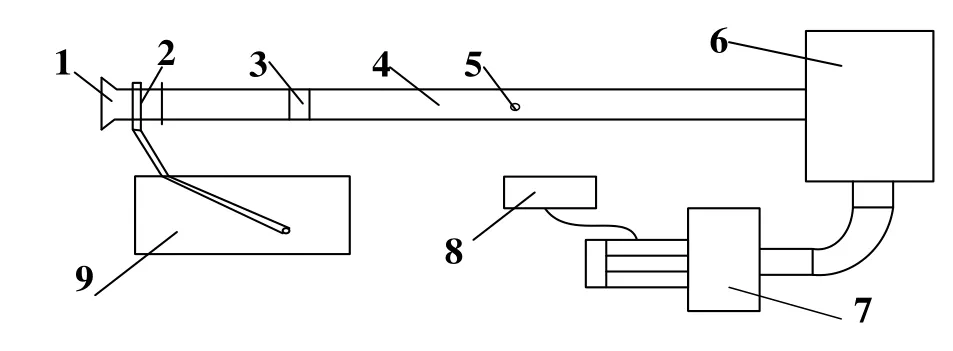
图1 基于吸入式喷嘴的风速标定装置

该装置采用负压吸入空气，管道吸入喷嘴口处装有压力采集环，可通过压差计测量管道内的平均风速。管中间设有风速计测孔，可以放入标准毕托管测量标准风管轴心风速大小。通过比对平均风速与标准毕托管轴心风速，获得修正值，从而获得该标定装置的标定修正值，用于后续风速仪的标定使用。本次实验所用的压差计（U=0.016%，k=2）和毕托管U=0.3%）。

1.2 实验方法

通过改变风机的频率来调整风管内的风速大小。每个工况下，通过读取标准流量管处的静压差及此时的大气压力、环境温度来计算得出标准风道的风速。然后在风速计测孔中通过毕托管测量管道中心点处的风速，将不同工况下的标准毕托管测得的风速与管口处流量管所测风速计算值比较。

1.3 实验原理分析

标准流量管是通过大气压力、空气温度、空气相对湿度和某截面的壁面静压4 个参数测试流量[15]。装置的实验原理是用伯努利方程计算流量管流量，根据质量守恒定律，由标准流量获得标准风道平均风速，再根据流体在管道内流动分布的特点，经标准毕托管测量风道轴心处的风速作为标准点风速，即风速计标定时的参照标准风速。

标准流量管所测的平均流速为：

式中，Δp1为压差，Pa；ρ为被测空气的密度，kg/m3，根据空气温度，大气压力计算得到[16]。

标准流量为：

式中，A1为标准流量管的喉部面积，m2；α为流量系数[16]；ε为空气膨胀系数[16-17]。

已知标准流量管的流量系数α与雷诺数Re[18]的对应数据：

式中，Re为标准流量管喉部的雷诺数。

空气膨胀系数ε与大气压和压差相关，对于Δp≤2,000 Pa，空气膨胀系数与两者的关系式：

实验时，所处环境的大气压力为103,080 Pa；标准风道内的雷诺数Re＞2,300，属于紊流状态[19]。

通过质量守恒定律[20]：

式中，ρ1、ρ2为标准流量管喉部和标准风道空气密度，kg/m3，两者近乎相等；v2为标准风道的平均风速，m/s；A2为标准风道截面积，A2=A1。

由式(1)和式(5)可得：

标准风道的实际风速通过标准毕托管测量：

式中，Vm为标准风道轴心风速，m/s；K为毕托管系数，本次实验，K=1；Δp2为压差，Pa。

标准风道的平均风速与轴心风速之间的关系用β（修正值）表示：

1.4 实验数据结果

该实验分为4 个工况，各工况的实验数据见表1。工况1、工况2、工况3 和工况4 的Re分别为34,968、66,858、90,995 和123,245。由表1 可知，风速的大小随标准流量管喉部压差的增大而增大。

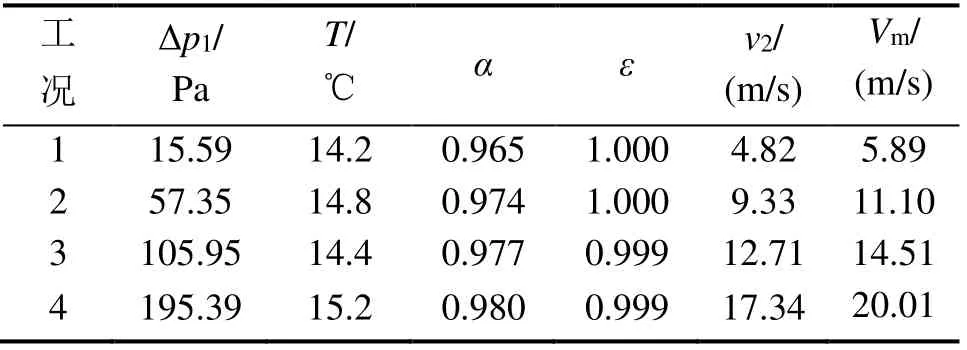
表1 不同雷诺数时实验数据结果

2 标准不确定度评定

2.1 用标准毕托管测量风速带来的不确定度u(Vm)

根据公式(7)得：

式中，E为重复性，cE=1；cK=1；cΔp2=0.5；cρ=-0.5。

毕托管的不确定度为U=0.3%（由标准给出）：u(K)=0.3%/2=0.15%。

压差变送器的不确定度u(Δp2)根据校准证书为U=0.016%，包含因子k=2，可得u(Δp2)=0.008%。

空气的密度由气体状态方程计算可得：

式中，T为空气温度，K。

本次空气温度的测量采用仪器为二等标准水银温度计，温度计的最小分度值为0.1 ℃，k=2，计算得到其不确定度u(T)=0.00009。

大气压的测量采用仪器为Delta 的HD2001 系列变送器，最大示值误差为±50 Pa，k=2，计算得到其不确定度u(pa)=0.0002。

把u(T)和u(pa)带入式(14)得出u(ρ)=0.057%。将u(Δp2)和u(ρ)的结果带入式(9)，得到各工况下，标准毕托管测量风速的不确定度，具体数据见表2。

表2 不同雷诺数时标准毕托管测量风速的不确定度

由表2 可知，标准毕托管测量风速的不确定度基本随着风速的增大而增大。在标准风速值大于14.51 m/s 时，该不确定度大于1%。

2.2 被检标准风道平均风速的不确定度u(v2)

根据式(6)得：

式中，cα=1；cε=1。

根据式(3)得α的不确定度：

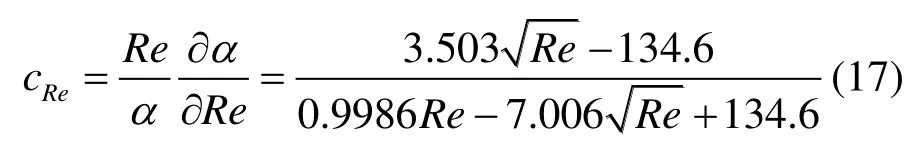
已知雷诺数Re=v1d/υ，υ为空气的动力黏度，可得雷诺数的不确定度为：

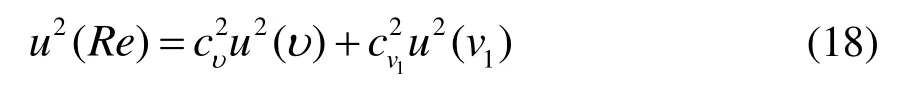
式中，cυ=-1；cv1=1。

α的不确定度，具体计算数据见表3。ε的不确定度约等于0，可忽略。

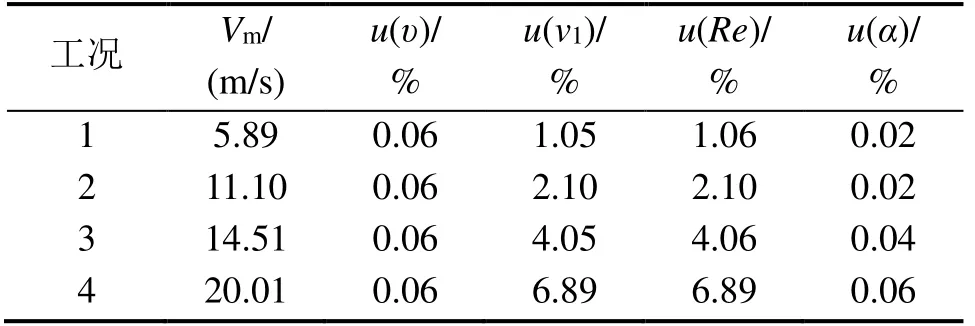
表3 不同雷诺数时α 的不确定度

将各数据带入式(15)，得到各工况下，被检标准风道平均风速不确定度，具体数据见表4。由表4 可知，被检标准风道的不确定度随着风速的增大而增大，且增长的幅度越来越快。

表4 不同雷诺数时被检标准风道平均风速的不确定度

2.3 标准风道的平均风速与标准毕托管所测轴心风速比值β 的不确定度u(β)

通过式(8)可以得到β的不确定度为：

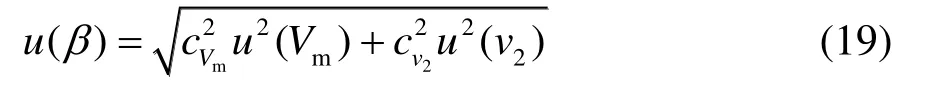
式中，mVc=1；2vc=-1。

根据式(19)，可得到β的不确定度，具体数据见表5。由表5 可知，β的不确定度随着风速的增大而增大。

表5 不同雷诺数时β 的不确定度

3 实验结果分析

标准风速为5.89 m/s 时，计算数据分析比较见图2 和图3。从图2 可知，Vm和v2的不确定度受多种因素的影响，重复性、K、压差和密度在该工况下对Vm的影响分别占84.7%、14.70%、0.01%和0.59%，重复性对Vm和v2的不确定度影响最大。

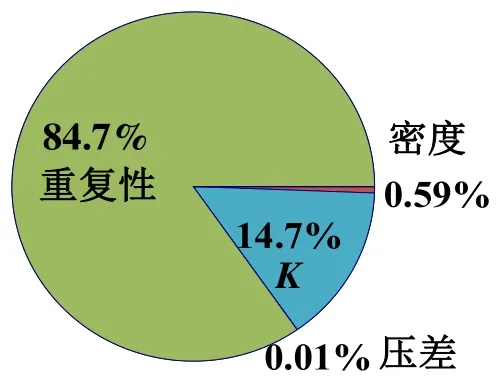
图2 参数对Vm 不确定度的影响

由图3 可知，β的不确定度随着风道内风速的增大而增大。在标准风道内的轴心风速在11.10 m/s内时，β的不确定度变化缓慢不超过1%。在标准风道内的轴心风速在11.10～20.01 m/s，β的不确定度增长的幅度变大，值大于1%。

图3 β 的不确定度随雷诺数的变化

4 结论

本文研究了一种吸入式喷嘴的风速标定装置通过将流量管转化的风速与通过标准毕托管所测的轴心风速之间的对比，通过对实验数据的处理分析，得到以下结论：

1）实验风速的不确定度受重复性的影响最大，以标准风速为5.89 m/s 时Vm为例，重复性在该工况下对Vm的影响占84.7%；

2）随着风道内风速的增大，风道内风速的不确定度的值基本呈上升趋势；

3）通过流量管所测的标准风道的平均风速与标准毕托管所测轴心风速比值β（修正值）的不确定度随着风道内风速的增加而增大，当风管内的风速超过一定值时，装置标定的可靠性会下降；该风速标定装置在11.10 m/s 以内数据可信赖性更高；

4）针对该装置重复性不确定度占比大的情况，风道设计要合理，比如增加整流稳定装置；要让电压稳定，变频器控制平稳来保证电机运转稳定；要在周围没有剧烈变化的环境下进行，防止周围环境的干扰。