考虑随机场景生成及优选技术的分布式能源站选型定容规划研究
王培汀,王 丹,贾宏杰,2,原 凯,宋 毅,张 梁
(1.天津大学智能电网教育部重点实验室,天津 300072;2.天津市智慧能源与信息技术重点实验室(天津大学),天津 300072;3.国网经济技术研究院有限公司,北京 102209;4.国网天津市电力公司经济技术研究院,天津 300171)
为缓解能源需求日益增长与环境保护日益迫切之间的矛盾,区域综合能源系统RIES(regional integrated energy system)备受各国关注[1-2]。分布式能源站作为RIES的核心,集成了多种能源耦合设备,涉及能源的供应、转换、存储等多个环节[3]。因此,对能源站各耦合设备进行合理的选型定容规划,是提高RIES的经济性,促进节能减排的重要环节。
传统的分布式能源站选型定容规划通常是基于确定性的规划场景,未考虑风、光等可再生能源的不确定性,未考虑用户负荷的用能不确定性[4-5],由此得到的分布式能源站选型定容规划配置在其实际运行过程中并非为最优结果。因此,在进行分布式能源站的选型定容规划时,需考虑各种不确定性因素的影响。如何在进行分布式能源站选型定容规划研究过程中对各种不确定性因素进行综合考虑,以及建立更加符合真实情况的随机场景是当前研究所面临的挑战之一。
目前国内外已有学者在对不确定性因素的处理方法上展开了相关研究。文献[6]考虑了风、光可再生能源的不确定性,基于风、光历史数据分别得到了风、光概率密度函数参数,用于描述风、光的不确定性;文献[7]采用区间数学规划方法考虑了不确定因素的取值区间,进而分别选取区间的上、下限,将不确定性问题转变为两个确定性问题进行处理,对于不确定性因素的随机特性考虑的较为粗糙;文献[8]考虑了风电的不确定性,通过蒙特卡洛随机抽样方法生成一定的不确定性场景并进行相应场景缩减,进而提出了一种基于场景法的两阶段规划求解策略;文献[9]提出了一种考虑多能负荷不确定性的区域综合能源系统鲁棒规划方法,该方法同样是以区间的形式考虑负荷的不确定性;文献[10]基于Copula 理论及时序重构技术研究了风速的相关性问题;文献[11]综合考虑了风、光不确定性和电负荷的不确定性,并且考虑了它们之间的相关性,生成了一系列随机场景,用于分布式能源系统的规划。
上述文献从不同角度对不确定因素进行了分析处理,但均未考虑各个不确定因素内部的时序自相关性。常用的随机场景生成方法不能表征实际场景下的风速、光照强度以及负荷内部的时序自相关性特点,因此,忽视各自不确定因素的时序自相关性而考虑不确定性,不能保证最终得到的随机场景真实合理。
综上所述,本文针对上述研究的不足提出了一种考虑随机场景生成及优选技术的分布式能源站选型定容规划方法。首先对各种不确定性因素进行建模,并提出了一种综合考虑时序自相关性和互相关性的随机场景生成及优选方法TA-MCRSGOM(Monte Carlo random scenes generation and optimiza⁃tion method considering time-sequence auto-correla⁃tion and mutual correlation);然后构建了随机场景下分布式能源站选型定容规划模型,在规划时兼顾了未来运行的经济性;最后通过相应算例进行对比分析,重点讨论在不确定性的风速、光照强度、电负荷和热负荷(以下简称为风、光、电、热)情况下,时序自相关性和互相关性对于分布式能源站优化配置的影响。
1 典型RIES 结构
RIES将传统分立的能源供应源、多样化供能网络及多能用户综合考虑,促进各种能源形式相互耦合,协同运行。同时RIES可充分利用当地风、光等自然资源禀赋,最终实现能源的综合利用,提高系统运行的经济性和环保性。
RIES 由多能网络、分布式能源站以及居民、商业、工业等不同功能的用户组成,涉及能源的“传输-转换-分配”等多个环节,其典型结构如图1 所示。作为RIES 能源耦合的核心,分布式能源站集成了热电联供CHP(combined heat and power)机组、燃气锅炉GB(gas boiler)、热泵HP(heat pump)、储能、风机WT(wind turbine)、光伏PV(photovoltaic)等设备,与不同区域负荷直接相连,可以协调区域间能源互联,为用户提供可靠、经济的能源供应。

图1 RIES 典型结构Fig.1 Typical structure of RIES
因此,本文针对分布式能源站,在考虑风、光、电、热各自时序自相关性以及它们之间的互相关性的情况下,研究分布式能源站内部耦合设备的选型定容规划方案。
2 不确定性因素建模
2.1 风速概率模型



2.2 光照强度概率模型

式中:PCAP,PV为光伏的额定容量;Ge为额定光照强度大小;Bg为光照强度基准值。
2.3 电、热负荷概率模型
电、热负荷的随机性服从正态分布,置信区间为95%,此时有1.96σ=0.2μ[17]。电、热负荷的概率密度函数f(L(m,s,t))可表示为
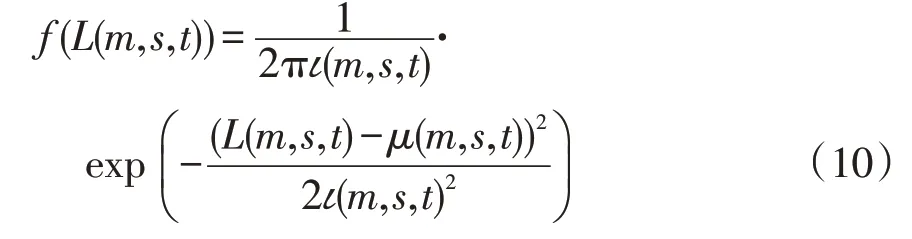
式中:L(m,s,t)为第m种负荷在s季节t时刻的负荷大小;μ(m,s,t)、ι(m,s,t)分别为第m种负荷在s季节t时刻的均值和标准差。
3 随机场景生成及优选方法研究
本文所构建的随机场景集考虑了风、光、电、热的不确定性。对于不确定性的分析,分别考虑了每个不确定性因素内部的时序自相关性和不确定性因素之间的互相关性,图2表述了时序自相关性和互相关性的含义,其中,时序自相关性描述了同一时间序列不同时刻的任意两个元素之间的关联程度,互相关性描述了不同时间序列之间的关联程度。

图2 时序自相关性与互相关性的含义Fig.2 Meaning of time-sequence autocorrelation and mutual correlation
3.1 时序自相关性建模


3.2 互相关性建模
在第3.1 节中,时序自相关性描述的是单一时间序列内部不同时刻的数值之间的关联,而互相关性则描述的是不同时间序列之间的关联程度。为了更好地描述非正态分布随机变量间的互相关性,本文引入Spearman 秩相关系数[18]。首先对随机变量按照从小到大进行排序,计算随机变量的秩,进而计算秩的Pearson相关系数。
两个随机变量X、Y间的Pearson 相关系数可表示为[10]

3.3 综合考虑时序自相关性和互相关性的随机场景生成及优选方法
为了使生成的随机场景集更贴合实际情况,将一年的风、光、电、热划分为过渡季、夏季和冬季进行处理。随机场景集的生成步骤如下。
步骤1 根据已有的典型风速、光照强度历史数据及电、热负荷规划数据,分别得到真实场景下各季度风、光、电、热各自的参考时序自相关性系数矩阵Ss,q,ref和风、光、电、热之间的参考互相关性系数矩阵ρs,ref。
步骤2 结合各不确定性因素的概率分布模型,利用蒙特卡洛进行随机抽样,得到N个初始不确定性场景,然后计算各场景中每个季度不确定性因素的时序自相关性矩阵,以风速为例,设过渡季风速F的时序自相关性矩阵为S1,1,通过对S1,1进行Cholesky分解可以消除由于随机抽样而产生的时序自相关性影响,即


式中:D为通过对S1,1进行Cholesky 分解得到的下三角矩阵;G为消除因随机抽样产生的时序自相关性后的N个过渡季风速序列所组成的矩阵。
步骤3 对G施加步骤1中求得的参考时序自相关性系数矩阵,可以得到比较符合真实情况的时序自相关性风速序列,即

式中:Dref为通过对S1,1,ref进行Cholesky 分解得到的下三角矩阵;Gauto为施加参考时序自相关性后的N个过渡季风速序列所组成的矩阵。
步骤4 通过上述步骤可分别得到三季度贴合真实时序自相关性的N个风、光、电、热序列,然后需要考虑风、光、电、热之间的互相关性,并通过粒子群算法筛选得到综合考虑时序自相关性和互相关性的随机场景集。由于惯性权重的设置对于粒子群算法的计算精度关系密切,惯性权重较大时算法有利于跳出局部最小值,便于全局搜索;惯性权重较小时算法有利于进行局部区域的精确搜索,便于收敛。因此本文通过采用惯性权重线性递减的粒子群算法,兼顾了算法搜索的全局性以及局部搜索的精确性,对所得到的N个风、光、电、热序列进行匹配,从中挑选出使得风、光、电、热之间的互相关性与真实场景下的互相关性误差最小的H个随机场景组成最终的随机场景集,实现以上全部过程的流程如附录图A1所示。其中粒子群算法的惯性权重ω(t)以及适应度函数min(Er)可分别表示为

式中:t为迭代次数;tmax为最大迭代次数;ωmax、ωmin分别为最大惯性权重和最小惯性权重;Er为互相关性误差;smax为所划分季节个数,本文将一年分为过渡季、夏季和冬季;qmax为不确定因素个数,本文为风、光、电、热共4 个;ρh,s为第h个随机场景s季节互相关性系数矩阵。
4 不确定性场景下分布式能源站选型定容规划模型
4.1 目标函数
不确定性场景下分布式能源站选型定容规划模型的目标函数为使分布式能源站投资、运行成本最低,其表达式为
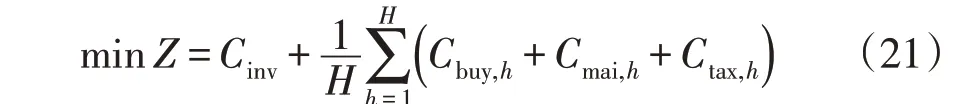
式中:Z为分布式能源站等值年规划总成本;Cinv为分布式能源站等值年投资成本;H为随机场景的数量;Cbuy,h、Cmai,h和Ctax,h分别为在第h种随机场景下分布式能源站等值年能源购置成本、设备运行维护成本和所产生的CO2折算后的等值碳税成本。

4.2 约束条件
分布式能源站选型定容规划模型的约束条件可分为规划类约束和运行类约束。规划类约束侧重于设备的固定投资方面,运行类约束侧重于分布式能源站中各设备的实时运行情况。
4.2.1 规划类约束

2)设备选型约束
规定当1 种设备存在多种型号时最多只能选择其中的1种,则相应的约束可表示为


综上所述,本文所建立的分布式能源站规划模型为混合整数线性规划模型,基于MATLAB 平台,使用YALMIP 软件包进行建模,并利用CPLEX求解器求得模型最优解[20-21]。
5 算例分析
5.1 算例设置
以北方某商业园区为规划对象,该园区建设规模为9×104m2,有较丰富的风能和太阳能资源,园区负荷主要为电、热负荷。根据其资源禀赋与用能特性,按照文献[22]中能源站的拓扑设计原则,构建了典型的分布式能源站拓扑结构,如图3所示。在此基础上,通过对该能源站规划不同类型和型号的能源设备,以实现综合利用风能、光能、电能和燃气,并为用户提供充足电能和热能的目的。对于该园区来说,待规划分布式能源站可考虑的能源设备有GB、CHP、HP、PV、WT、电储能和热储能设备。其中,GB、CHP和HP需要考虑设备型号和容量大小,本文定义的设备型号是用于区分同一种设备具有不同的转换效率和单位容量造价的情况;PV、WT、电储能和热储能仅规划设备容量。为了保证分布式能源站运行的经济效益和环境效益,需要对上述设备进行合理规划。可用于规划分布式能源站的设备如图4所示。

图3 待规划分布式能源站拓扑结构Fig.3 Topology of distributed energy station to be planned
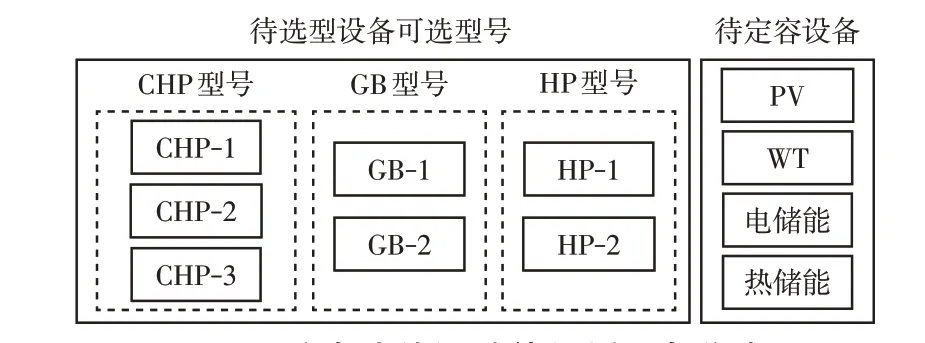
图4 分布式能源站待规划设备集合Fig.4 Collection of equipment to be planned for distributed energy station

5.2 不同随机场景集生成方法对比
为验证所提综合考虑时序自相关性和互相关性随机场景生成及优选方法的合理性,分别采用蒙特卡洛随机抽样技术MCRS(Monte Carlo random sampling)、考虑互相关性的蒙特卡洛随机抽样技术MCMCRS(Monte Carlo random sampling considering mutual correlation)以及本文所提TA-MCRSGOM 进行对比分析。分别通过采用以上3 种技术抽取50个随机场景集样本,选取随机场景中3个典型日的光照强度为例,与历史典型场景光照强度的结果对比如图5所示。
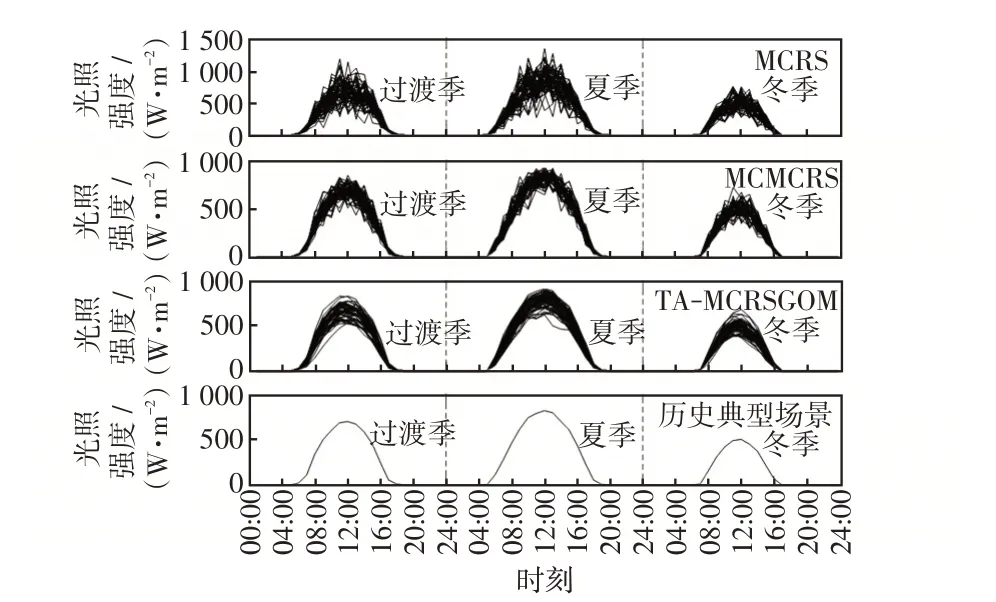
图5 不同方法产生的光照强度与历史典型场景对比Fig.5 Comparison between light intensity generated using different methods and that in typical historical scenes
由图5 可知,传统的MCRS 方法所得到的随机场景集十分粗糙,光照强度的变化情况与真实场景差异较大。而在此基础上考虑不同因素之间的相关性的MCMCRS方法可以得到一定程度的改善,但仍与实际典型场景有较大出入。若采用以上两种方法所生成的随机场景进行分布式能源站规划将会造成较大误差。由图5可知,本文所提综合考虑光照强度的时序自相关性和光照强度与其他因素之间的互相关性,所得随机场景光照强度的变化情况更符合真实场景,因而采用本文所提TA-MCRS⁃GOM 进行随机场景下的分布式能源站规划研究将更符合实际情况。
第5.2节是以光照强度为例定性分析了本文所提TA-MCRSGOM生成的随机场景相比于其他方法的优势,从定量的角度,根据3 个季节场景生成方法所得到的50 个不确定性场景,分别计算各场景的时序自相关性系数矩阵和互相关性系数矩阵,并与第3.3 节中得到的参考时序自相关性系数矩阵Ss,q,ref和互相关性系数矩阵ρs,ref对比,将平均误差分别列于表1,由表1可知,本文所提方法的误差明显小于其他两种方法,从而验证了本文所提方法的有效性。

表1 不同随机场景生成方法的平均误差Tab.1 Error analysis of different random scenes generation methods%
时序自相关性的误差计算公式可表示为

5.3 场景缩减合理性验证
本文首先采用蒙特卡洛方法随机生成1 500个随机场景,对所得到的各不确定性因素样本施加参考时序自相关性,得到考虑时序自相关性的风、光、电、热样本。通过采用惯性权重线性递减的粒子群算法从时序自相关性样本中筛选出较为符合真实场景互相关性的随机场景,筛选数量为50,从而完成了场景优选,得到了最终的随机场景。
图6对比了所筛选出的50个场景在1 500个时序自相关性样本中的分布情况,由图6 可知,所得到的随机场景集较为均匀地分布于自相关性场景集的中心,具有很好的代表性。

图6 优选后场景在时序自相关性样本中的分布情况Fig.6 Distribution of post-optimization scenes in timesequence autocorrelation samples
5.4 确定性对比场景设定
传统的分布式能源站选型定容配置研究大都基于确定性的典型场景[4,5,26,27],将其作为能源站规划求解的输入条件,而未考虑到风、光资源以及电、热负荷的不确定性所产生的影响。
为了证明风、光、电、热的不确定性对于分布式能源站规划所产生的影响,参照文献[5]的做法,将典型日的风速和光照强度以及电、热负荷的规划数据设为确定性场景,分别与传统的MCRS 方法所得到的随机场景集、MCMCRS方法得到的随机场景集以及TA-MCRSGOM 得到的随机场景集作为对比,以探究在确定性场景和不同随机场景下分布式能源站的规划结果。确定性场景和TA-MCRSGOM方法所得到的随机场景集的典型日对比如图7所示。

图7 确定性场景和不确定性场景对比Fig.7 Comparison between deterministic and uncertain scenes
5.5 分布式能源站优化配置分析
通过考虑不同方法所建立的随机场景集,以及第5.4 节构建的确定性规划场景,可分别得到不同场景下分布式能源站各设备的选型定容结果,如表2 所示。由表2 可知,在不同情况下所得到的规划结果差异较大,具体分析如下。

表2 不同场景下分布式能源站规划结果Tab.2 Planning results of distributed energy station in different scenes
(1)设备选型。不同随机场景集和确定性场景所得结果大体一致,这是因为虽然输入场景不同,但目标都是使分布式能源站投资运行成本综合最优。在设备选型上的差别体现在GB 设备上,确定性场景未规划GB,其他随机场景集选择了GB-1,主要是因为确定性场景下热负荷较小,而随机场景集中有些场景热负荷较大,因此在规划中选择了GB-1,起到负荷高峰时段的调峰作用。
(2)规划容量。本文所提方法对GB 规划容量明显大于其他两种方案的规划容量,这是因为,其他两种方案所生成的随机场景不符合实际情况,所生成的热负荷曲线波动较大,CHP受爬坡率约束的影响不能及时满足波动性较大的热负荷需求,因此只能增加供热容量。对于CHP 尤其HP 设备,MCRS、MCMCRS 方案设备的规划容量均大于本文所提方法的规划容量。从供热角度,GB 相比于CHP 和HP 具有较大的成本优势,若减少GB 规划容量,将GB 的部分供热能力转移到成本较大的CHP 或者HP 设备上,那么在平时供热过程中CHP或者HP会出现较大的容量冗余情况,而这部分冗余容量也只在“调峰”时起作用。综上,虽然本文所提方法规划的GB 容量相对偏大,但最终规划成本反而较低。
不同随机场景集下的供热设备规划容量均大于确定性场景的规划容量,但由于热储能设备造价较低,因此把热储能设备规划到所允许的最大容量。随机场景集中的热负荷具有一定的不确定性,在某些场景下热负荷较高,所以总规划容量相比于确定性场景要大。同时发现不同随机场景集之间的供热规划容量也有较大差距,本文所提方法供热规划容量最小,MCMCRS 次之,在MCRS 下供热规划容量最大。这是因为MCRS 和MCMCRS 所产生的随机场景未考虑到负荷的时序自相关性,负荷曲线波动过大,而机组受到爬坡率的约束不能即时满足负荷的变化需求,因此对于供热设备的规划容量偏大。
(3)供电设备容量。确定性场景和随机场景集设备规划的差异性较大,对于电储能设备,在随机场景集下电储能设备的规划达到所允许的最大额定容量。这是因为电储能设备具有良好的“削峰填谷”作用,提高了在不确定性情况下供电的稳定性。由于风、光均具有一定的不确定性,所以对于WT、PV的规划容量综合来看相比于确定性场景较小。不同随机场景集所规划WT、PV容量也具有一定差异,由于风速相比于光照强度具有更大的波动性,而MCRS和MCMCRS方法所产生的风速波动更大,因此其规划的风机容量较小,但由于光照强度较大,在这两种随机场景集下所规划的光伏容量相对较大。
表3 对比了不同场景下分布式能源站的投资和运行成本。可以发现确定性场景下系统的总成本要低于其他方法产生的随机场景下的成本,主要体现在能源购置费用上。这是因为在确定性场景下,认为风、光、电、热均处在典型日不变,但是在实际情况下,无论是风光资源,还是电热负荷,均存在着一定的不确定性,而确定性场景没有考虑这一实际情况,按照理想的确定性运行状态进行了规划,虽然理论计算成本较低,但实际情况下将会有较大偏差。

表3 不同场景下分布式能源站运行投资成本对比Tab.3 Comparison of investment costs for distributed energy station operation in different scenes 104¥
现选取确定性场景下能源站的规划结果,分析其在TA-MCRSGOM方法所产生的随机场景下的运行情况。发现确定性场景下所规划的分布式能源站无法满足部分随机场景下的供能需求。对于电负荷缺额,尚可由电网来补足,而对于热负荷缺额,由于确定性场景下供热设备规划容量较小,因此无法满足供热需求。通过计算可知,在确定性场景下规划设备最大热出力为366 kW,其中CHP 最大热出力为196 kW,HP最大热出力为80 kW,热储能设备最大热出力为90 kW,根据本文所建立的随机场景集可知,其中热功率最大为444 kW,在此随机场景下依然有78 kW的热功率缺额,无法满足随机场景下的热负荷需求。因此,在本文所提TA-MCRS⁃GOM 方法所建立的随机场景集下分布式能源站的规划结果,相比于确定性场景的规划结果不仅能适应更加复杂的不确定性运行场景,而且其投资成本也低于确定性场景规划结果。
不同随机场景下所规划的分布式能源站运行投资成本也存在较大差异,对于投资成本,如上文所述,由于采用MCRS 和MCMCRS 方法所产生的风、光、电、热场景不符合真实场景下的变化情况,即不满足实际情况下的时序自相关性,不同时刻之间的值波动较大,而CHP机组出力受到爬坡率的约束,因此为了满足负荷需求,所规划的容量偏大,投资成本较高,而运行成本与设备的投资成本密切相关,因此也存在一定差异。相比之下,本文所提TAMCRSGOM 方法下的规划结果既可以有效降低能源站投资成本,又可以满足多种随机场景下的运行需求,而且其所建立的随机场景集更加符合真实情况。
5.6 随机场景下所规划能源站的运行特性分析
为了探究TA-MCRSGOM方法下所规划能源站的运行特性,需要从以上随机场景集中选取相应的随机场景作为运行分析的输入条件。随机场景的选取原则为选择随机场景集中较为极端的场景,可采用以下方法得到。
(1)分别计算随机场景集中风、光、电、热3 个典型日之和的期望,即

式中,Vq(h,t)为场景h下不确定因素q在t时刻的值。
(2)计算不同随机场景下风、光、电、热的偏移度,从中选取上述4种不确定性因素各自偏移度最大的场景作为运行分析的输入条件,由此可确定4个随机场景。不同场景的偏移度计算公式为
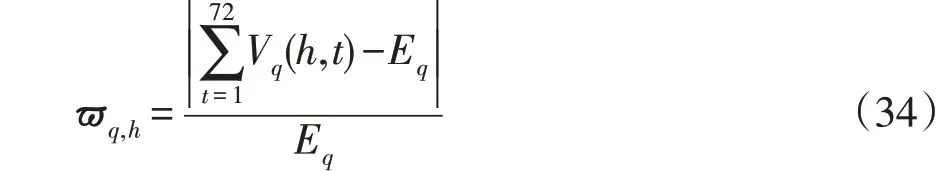
(3)挑选综合偏移率最大的场景作为用于运行分析的第5个随机场景,综合偏移度计算公式为

通过采用上述方法可以得到用于分析能源站运行特性的5个随机场景,其中不重复场景有4个,分别为场景6、场景40、场景41和场景49,各场景典型日的相关数据见附录图A6~A9。图8为场景40中3个典型日下分布式能源站的运行特性,其他3个场景典型日能源站的运行情况见附录图A10~A12。
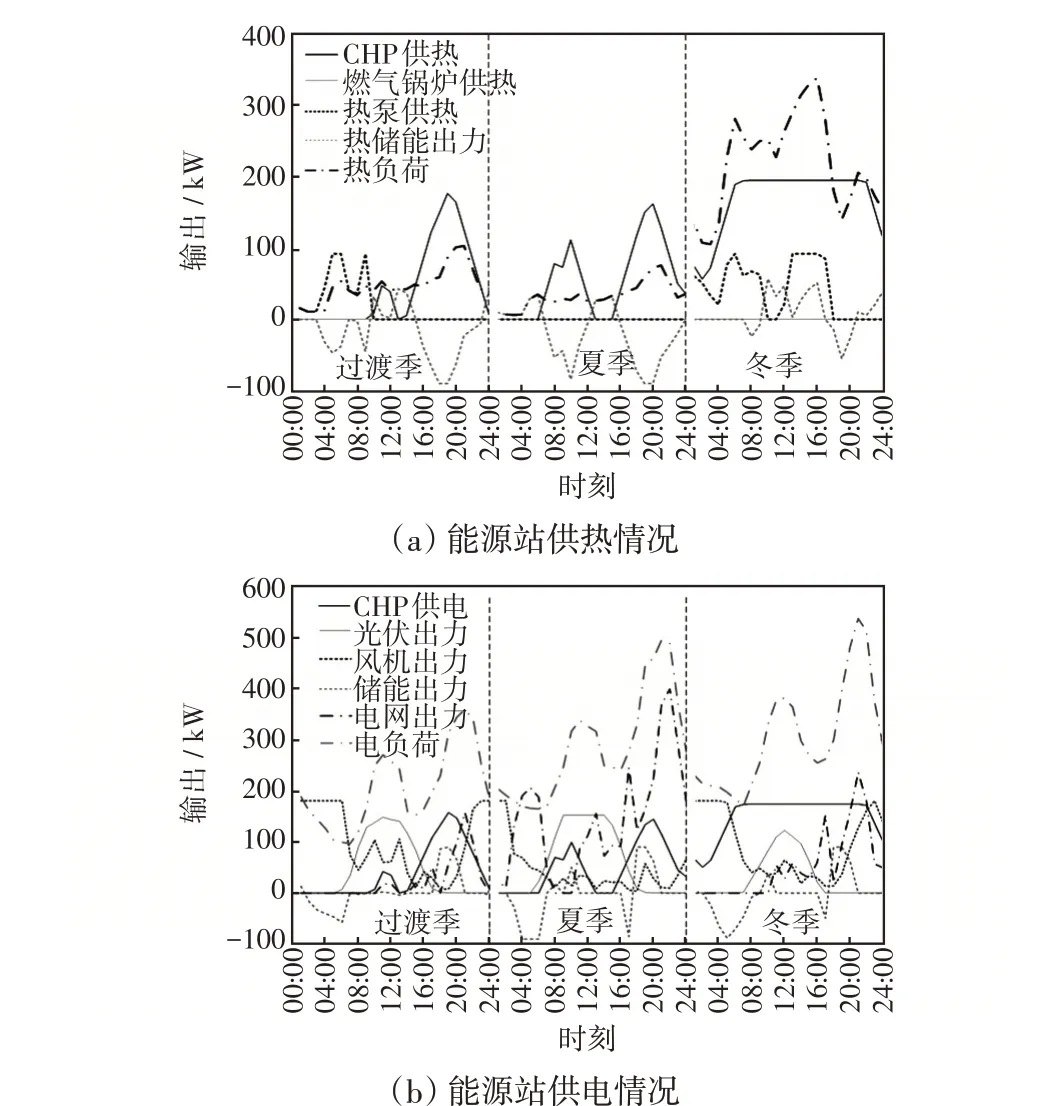
由图8(a)可知,由于过渡季和夏季热负荷较低,因此主要依靠CHP 机组就能满足用户供热需求,所产生的多余热能储存在热储能设备中。冬季热负荷较大,CHP机组容量有限,此时HP机组开始出力,能满足一天中大部分热负荷需求,但在热负荷峰值时段,则需要GB参与调峰出力。由于GB只参与调峰,因此对于GB规划的容量相对较低。
图8(b)展示了分布式能源站供电情况,由于WT 和PV 在运行的经济性和环境效益方面都具有巨大优势,因此WT和PV优先出力供应负荷。当可再生能源出力较低时,在谷时电价时段,电价相比于天然气价格存在一定优势,此时电网增加出力供应负荷,而在其他时段则由CHP机组增加出力供应负荷。

图8 场景40 典型日下分布式能源站运行特性Fig.8 Operating characteristics of distributed energy station on typical days in scene 40
综上可知,以选取的4 个场景典型日为例,验证了在综合考虑风、光、电、热各自的时序自相关性和它们之间的互相关性时,所规划得到的分布式能源站能够适应各种随机场景,并在运行过程中可以兼顾经济性和环保性。
6 结 论
本文研究了考虑多种不确定性因素的随机场景生成及优选方法,在此基础上进行了分布式能源站选型定容规划研究。主要工作如下。
(1)针对各不确定性因素进行建模分析,提出了TA-MCRSGOM,得到了用于分布式能源站规划的随机场景集。通过与各种抽样方法产生的随机场景对比,证明了本文所提方法能更加合理的反映风、光、电、热的变化特点,因此产生的随机场景更加符合实际情况。
(2)在生成随机场景集的基础上,构建了随机场景下分布式能源站的选型定容规划模型,该模型为混合整数线性规划模型,通过CPLEX 求解器可以得到最优解。
(3)在确定性场景和不同随机场景集下,对分布式能源站的规划结果进行对比,验证了本文所提TA-MCRSGOM 能够精准地考虑不确定性因素的时序自相关性和互相关性,从而对分布式能源站进行规划,其结果不仅能适应复杂的不确定性运行场景,而且其投资成本也低于确定性场景及其他随机场景集下的规划结果。
(4)分析了所规划的分布式能源站在随机场景下典型日的运行特性。通过考虑分时电价的影响以及可再生能源出力特点,各设备协同出力,可以较好地适应园区供能需求的不确定性。
另外本文对上述问题的研究具有局限性:①根据典型日的规划数据构建的随机场景,仅为能源站运行的一般情况,未考虑极端场景;②所研究的综合能源系统规模较小,未考虑分布式能源站输入侧以及输出侧的网络拓扑;③对于能源站中设备发生故障的可能性、故障发生类型以及故障发生后的应对措施未作考虑。这些将在后续工作中进行进一步研究。
附录A
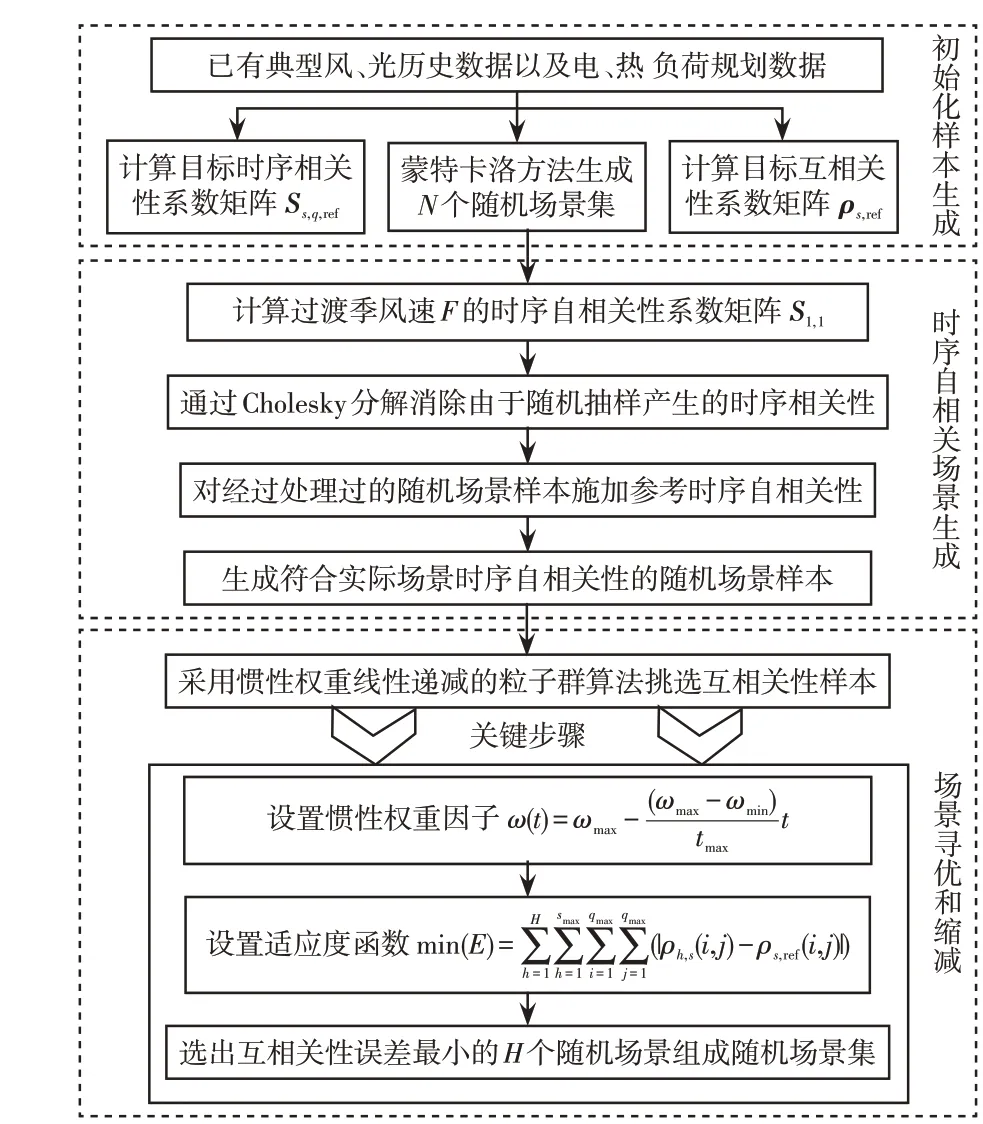
图A1 随机场景样本生成策略Fig.1 Random scene samples generation strategy

图A2 历史典型日风速曲线Fig.2 Wind speed curve on typical historical days
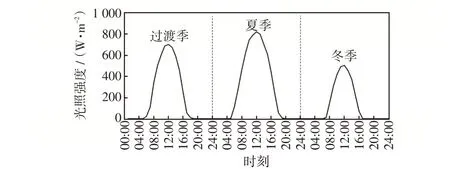
图A3 历史典型日光照强度曲线Fig.3 Light intensity curve on typical historical days
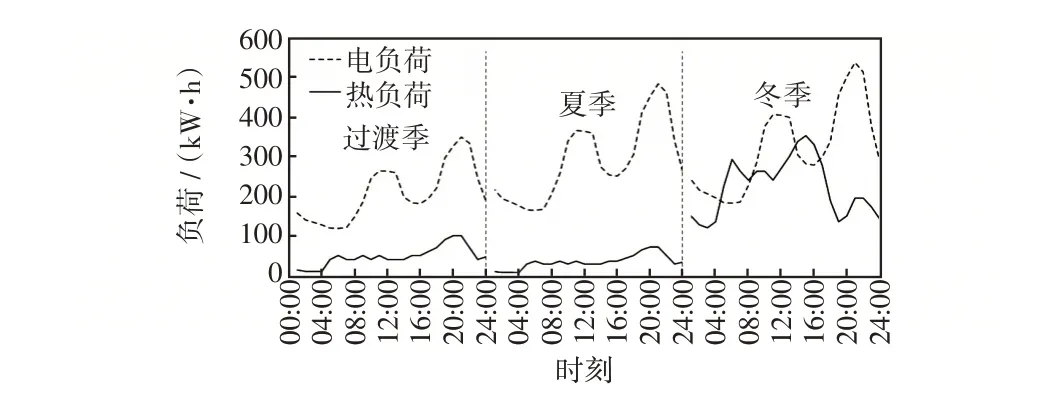
图A4 电热负荷规划数据曲线Fig.4 Curves of electricity and heat load planning data
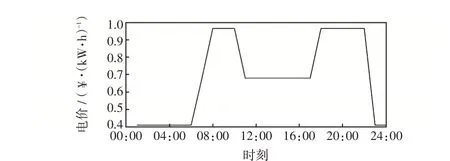
图A5 分时电价曲线Fig.5 Curve of time-of-use electricity price
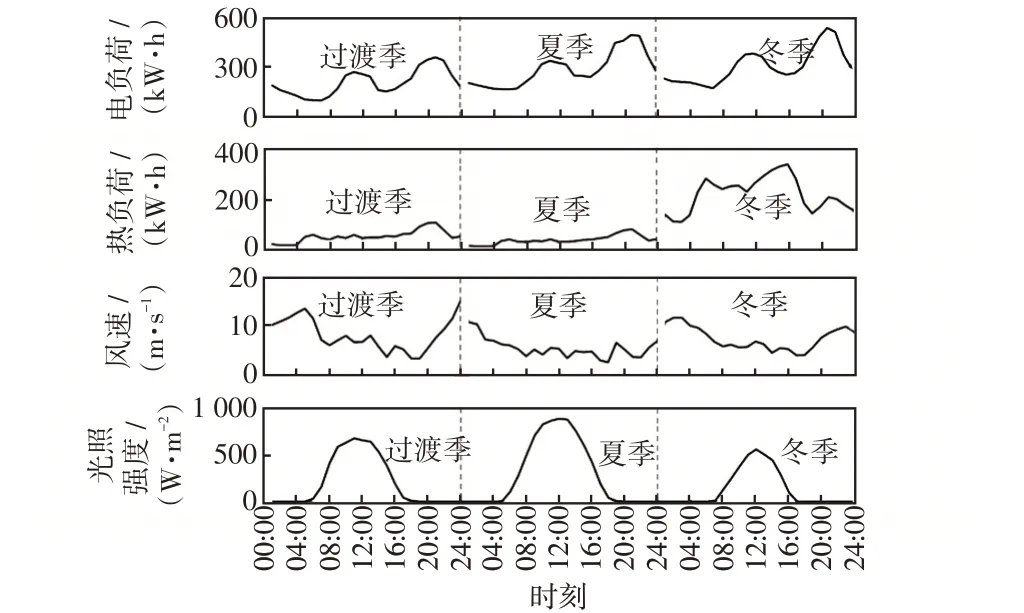
图A6 随机场景6 典型日的风、光、电、热数据Fig.6 Data of wind speed,light intensity,electrical load,and heat load on typical days in random scene 6
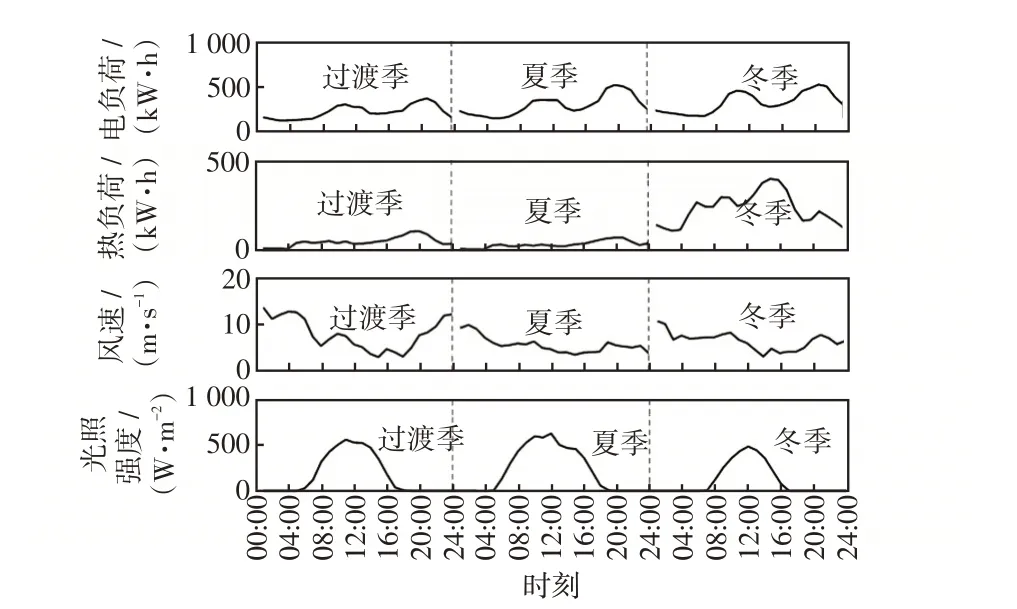
图A7 随机场景40 典型日的风、光、电、热数据Fig.7 Data of wind speed,light intensity,electrical load,and heat load on typical days in random scene 40
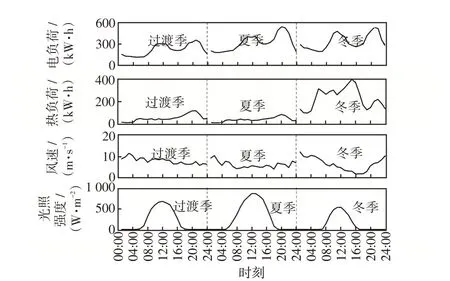
图A8 随机场景41 典型日的风、光、电、热数据Fig.8 Data of wind speed,light intensity,electrical load,and heat load on typical days in random scene 41
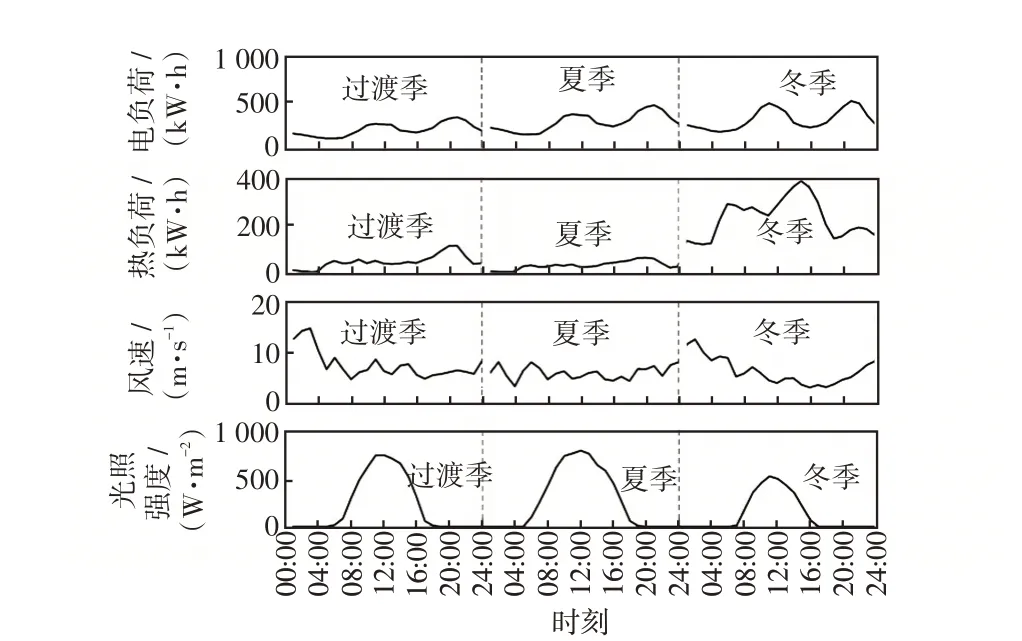
图A9 随机场景49 典型日的风、光、电、热数据Fig.9 Data of wind speed,light intensity,electrical load,and heat load on typical days in random scene 49
图A10 场景6 典型日下分布式能源站运行特性Fig.10 Operating characteristics of distributed energy station on typical days in scene 6


图A11 场景41 典型日下分布式能源站运行特性Fig.11 Operating characteristics of distributed energy station on typical days in scene 41

图A12 场景49 典型日下分布式能源站运行特性Fig.12 Operating characteristics of distributed energy station on typical days in scene 49
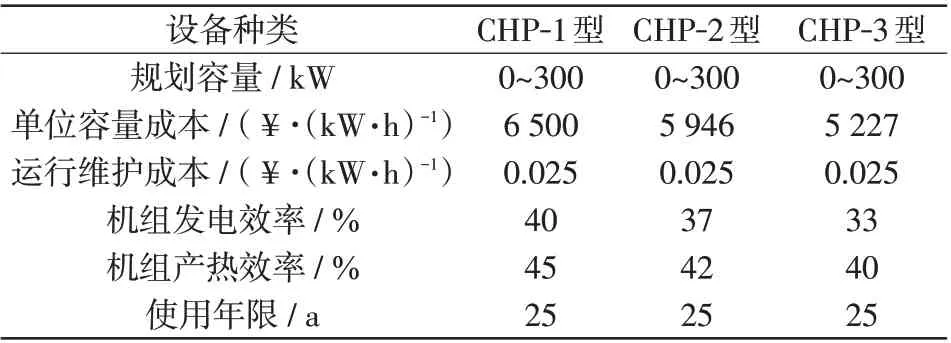
表A1 CHP 机组各型号设备参数Tab.A1 Equipment parameters of different types of CHP unit

表A2 热泵、燃气锅炉各型号设备参数Tab.A2 Equipment parameters of different types of heat pump and gas boiler
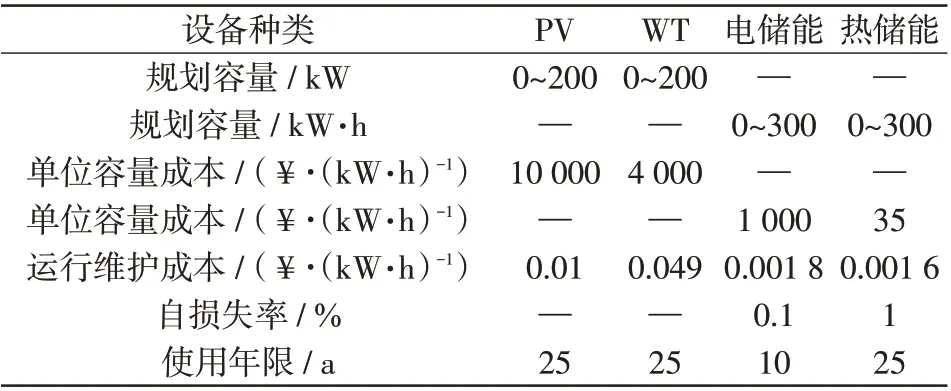
表A3 其他设备参数Tab.A3 Parameters of other equipment

