台风天气下配电系统韧性提升策略

邹 波，孙 可，胡成鹏，戴 攀，朱小军，叶承晋

（1.国网浙江省电力有限公司经济技术研究院，杭州 310020；2.国网浙江省电力有限公司，杭州 310007；3.浙江工业大学信息工程学院，杭州 310023；4.国网杭州市富阳区供电公司，杭州 311400；5.浙江大学电气工程学院，杭州 310027）

近年来，由于极端天气的影响，配电网大规模故障事故发生率不断上升。根据美国国家海洋与大气管理局、美国气象学会发布的《2016 气候状况报告》可知，2016 年极端天气事件显著增加[1]，在该年度中，极端天气造成的灾害事件发生797 次，相较于2010年，增加了46%。每年夏季的台风天气为我国造成数百亿元的经济损失，也为配电网的稳定可靠运行带来严峻挑战。为了抵御极端灾害带来的严重影响，提升配电网韧性作为配电网现代化的一项重要任务，逐渐成为学者研究的热点。

配电系统韧性可以定义为，在面对极端灾害时，配电系统能够做到抵御、适应和快速从灾害中恢复[2]。目前提升配电系统韧性的研究可分为两个方面：韧性运行，韧性规划。韧性运行主要关注灾害发生时或发生后电力系统的应对和恢复策略。文献[3]提出两阶段优化模型联合优化并求解配电网的灾后修复、系统恢复和网架重构策略，从而极大缩短了电网灾后重建的时间。韧性规划则关注灾害发生前系统的防灾能力和应对策略。文献[4]研究在配电网架规划阶段考虑灾难天气的因素，通过建立两阶段模型来求解具有高韧性的网架规划方案。相较于文献[4]在较长时间尺度考虑韧性规划，文献[5]则在较短时间尺度上，针对飓风天气，通过灾前临时加固杆塔和植被管理来提升配电系统的抗灾能力，并通过鲁棒优化模型求解加固策略。

针对台风天气，灾前提升配电系统韧性的方法主要有电网加固和配置分布式电源DG（distributed generation）或 储 能 装 置ESS（energy storage sys⁃tem）。电网加固有多种措施，例如架空线路加固，植被管理等。其中，在我国南方台风的极端天气中，杆塔的倒塌是导致大部分停电事故发生的原因[6]，因而架空线路加固一般采用加固杆塔的方式。在实际工程中，通常对升级之前出过问题的杆塔或根据经验进行有针对性的加固升级，该做法工程量大，实际抗灾效果差，因而亟需通过定量建模的方式对配电系统的加固提供决策支持。

目前，已有学者针对灾前加固配电网进行了广泛研究。文献[7]利用在不同的极端天气条件下，加固线路和提高故障设施修复速度等方式来提升系统韧性。文献[8]基于配电网功率拓扑图来辨识配电网薄弱环节，进而有针对性的加固薄弱环节以提升配网韧性。多种类型的DG和ESS接入配电网可以在灾害故障后，为本地重要负荷提供供电支撑。然而，上述研究没有综合考虑线路加固和DG 与ESS 的有效布点对故障区域内关键负荷的支撑；此外，忽略加固后线路的故障模型，并将其当作零故障线路建模这一思路也是不合理的。

本文针对台风极端天气，建立3 阶段韧性提升优化模型。第1 阶段确定加固线路和加固类型以及对分布式电源进行选址定容；第2 阶段在第1 阶段的基础上，以台风对配电系统造成损失最大化来确定故障线路的位置；第3 阶段是在“最坏情况”下，使停电损失最小化。通过降低配电系统在面对台风天气时发生故障的概率，最大化系统防御台风天气能力的同时保证所得策略的经济性。相较之前已有的研究，本文有以下两点创新：①在韧性提升策略中，根据系统故障规模综合优化线路加固和DG 与电池的选址定容，使所求策略更符合实际配网运行的需要；②根据负荷重要性对负荷进行等级划分，进而最大限度地保证故障区域内关键负荷的供电可靠性。对于3阶段优化模型，本文将模型中的第2层和第3层模型描述为max-min结构，并通过对偶理论转换成单层模型，从而将3层模型转换为双层模型，并设计了高效的迭代算法来求解转换后的双层模型。最后通过算例分析表明了所提模型和方法的有效性。

1 架空线路故障模型分析

架空线路故障模型主要考虑风速对不同类型的杆塔的影响，通过杆塔故障模型计算出配电线路在各种极端天气条件下的故障概率。

架空线路主要由杆塔和导线组成，但在极端天气灾害期间，杆塔在强风和暴雨的环境中容易发生损坏，且线路中的任一杆塔损坏都会导致整条线路的故障。因此可把杆塔故障模型建成1 个串联系统[9]。1 条线路的故障概率需要对线路内的每个杆塔进行故障模型分析。假设架空线路中的每个杆塔的故障概率是独立的，则可对极端天气导致的架空线路发生故障的概率建模，即

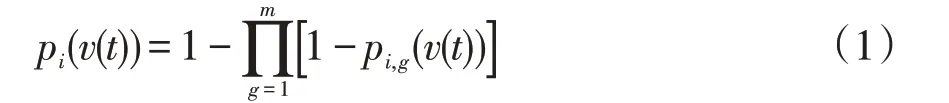
式中：pi(v(t))为线路i的故障概率；m为线路i中的杆塔数量，t为当前优化时段；pi,g(v(t))为与台风时速相关的函数，其用来表示在线路i上的第g个杆塔的故障概率，可用对数正态累积分布函数表示[10]，即

式中：v(t)为台风风速；mR为阻尼系数，ξR为强度测度的对数标准偏差，这两类参数会在杆塔采取不同加固策略时进行对应改变。式（2）将杆塔的故障概率表示为台风风速的函数。

2 3 阶段鲁棒优化模型

本文提出了3阶段鲁棒优化模型，旨在“最坏”的故障情况下，最小化切负荷量和投资成本。3 阶段优化模型如图1所示。第1阶段模型确定需要加固的线路和DG以及ESS的选址定容；第2阶段模型以使配电系统损失最大化，即“最坏情况”，来确定发生故障的线路；第3阶段模型以最小化故障线路引起的切负荷成本为目标进行优化。

图1 3 阶段优化模型Fig.1 Three-stage optimization model

2.1 3 阶段鲁棒模型的搭建

3阶段鲁棒优化模型可表示为

2.2 第1 阶段优化模型搭建

式中：Ee,t+1为t+1 时刻第e个ESS 的荷电状态；δe为第e个ESS的放电效率；Δt为优化时间间隔。

在本文中，仅考虑ESS 的放电行为，并假设安装的ESS 均充电至最高容量，以应对可能发生的故障。

2.3 第2 阶段优化模型搭建

加固和未加固两类线路发生故障的不确定性集合可表示为

2.4 第3 阶段优化模型搭建

第3阶段的优化模型可表示为

式中：Ri为线路i的电阻；Xi为线路i的电抗；M为一个足够大的数。如果线路i发生故障，即zi,t=1，由式（23）～（24）可得Pi,t=0，Qi,t=0。

系统电压和切负荷系数限制可分别表示为

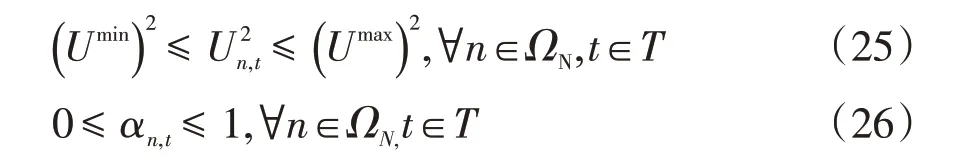
3 求解算法

为方便描述，将第2.1节的3阶段模型简化为

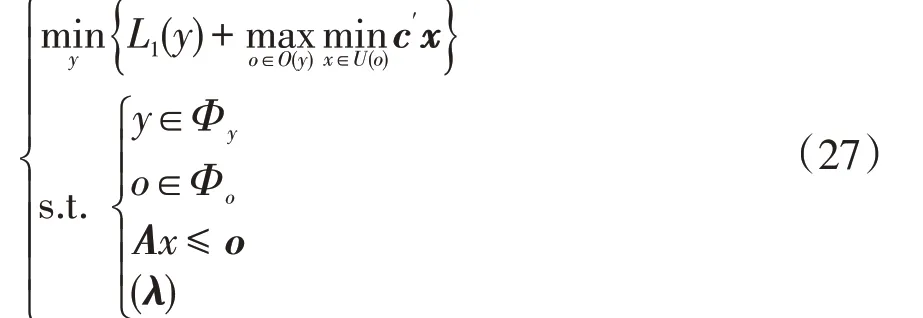
式中：c′x=L2(x)，c′为矩阵c的转置；c为成本系数，可由式（18）决定；x为第3 阶段的决策变量；Φy表示式（5）～（12）；Φo表示式（13）～（17）；约束Ax≤o表示式（19）～（26）；λ为其对应的对偶变量。对上述目标函数的max-min问题进行对偶变化可得如下形式。

基于式（30），设计如下迭代算法，算法流程如图2所示，算法步骤如下。

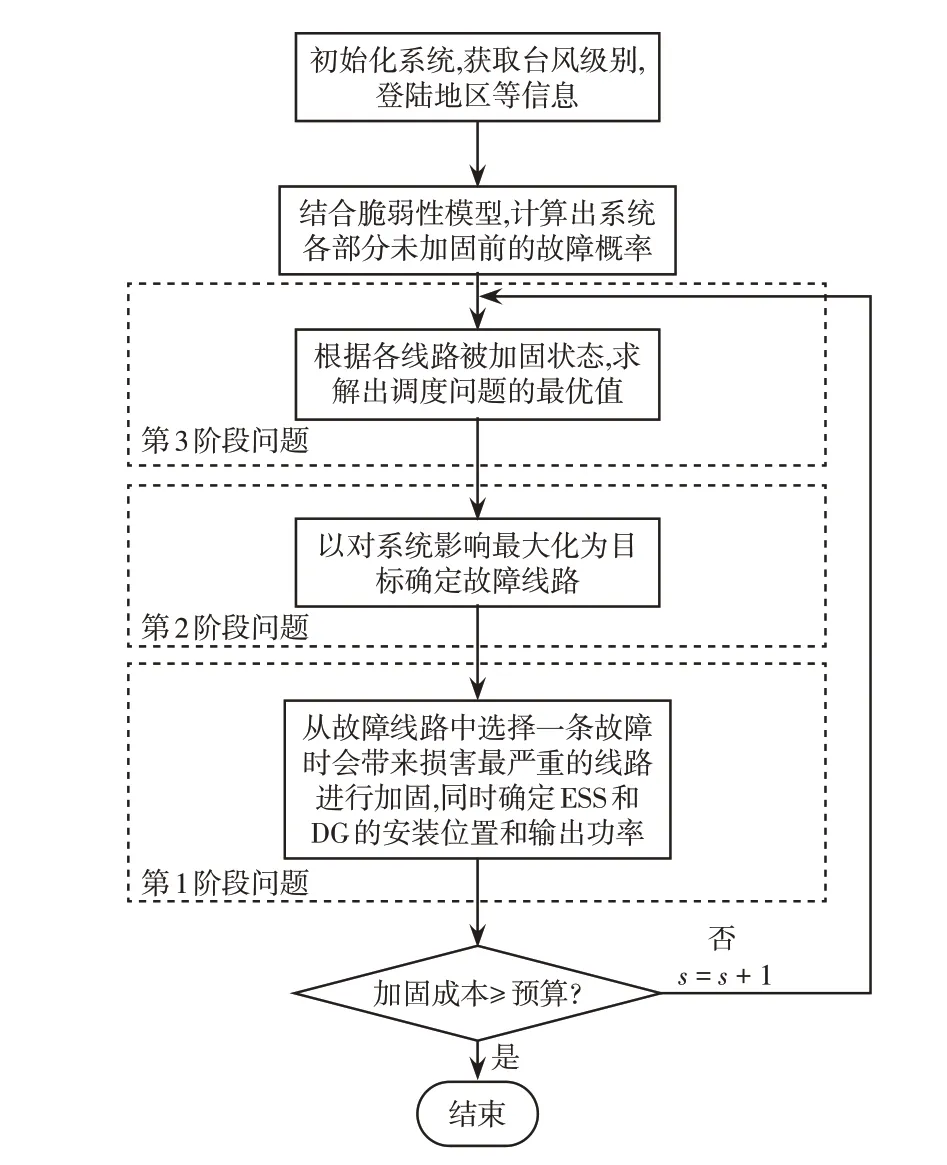
图2 算法流程Fig.2 Flow chart of algorithm

步骤1 初始化。设置台风参数（如台风等级等）和迭代次数s=0。计算配电系统加固和未加固两种情况下架空线路的故障率。

步骤2 计算如下优化问题。

将式（31）最优结果表示为{λs,os}，其中，λs为第s次迭代时对偶变量的取值，os为第s次迭代时不确定变量的取值。

步骤3 根据最优解找出对切负荷影响最大的关键线路，并将其加入关键线路集合。

步骤4 针对步骤3 的关键线路集合进行加固，求解如下优化问题。

根据目标函数的最优解判断加固成本是否超过预算。如果是，则结束程序。如果否，则设置s=s+1，返回到第2步。

4 算例分析

采用改进后的IEEE 33节点测试系统进行算例分析，如图3所示，其中，LP为负荷节点位置。本文的算例中考虑2种DG和3种ESS设备，其具体安装节点位置在3 阶段模型中求解得出。为了评估台风对配电系统的影响，基于统计建模方法，通过其静态和动态梯度风场对台风进行建模[11]，以模拟台风的空间分布、强度和最大风速半径。根据上述信息和测试系统的模拟数据，由式（1）～（2）计算配电线路的故障概率。

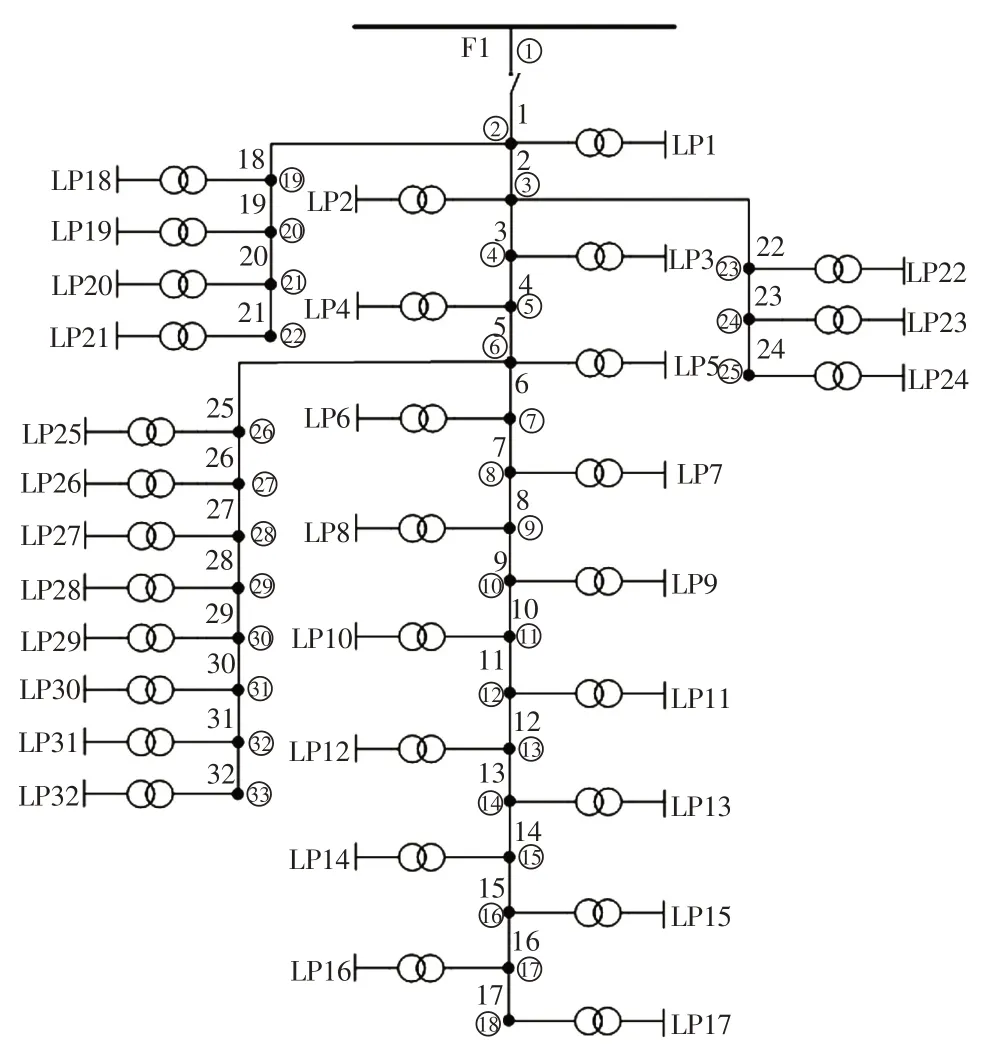
图3 测试系统拓扑Fig.3 Topology of test system

4.1 系统参数设置

杆塔在加固和未加固状态下的故障概率参数以及对应的加固费用见表1。电压范围设置在0.95～1.05，不确定预算w设置为0.005，切负荷成本系数cLoad设置为40¥/（kW·h），则一级负荷的切负荷成本为40 ¥/（kW·h），二级、三级负荷的切负荷成本分别为10¥/（kW·h）和8¥/（kW·h）。加固成本预算设为13 × 104¥，DG 和ESS 具体参数见表2和表3。各时段下节点总负荷需求和各节点负荷需求如图4～5 所示。一般台风登陆后的12 h 以内为配电系统遭受破坏高发期，故本文优化时段为台风登陆后的前12 h。

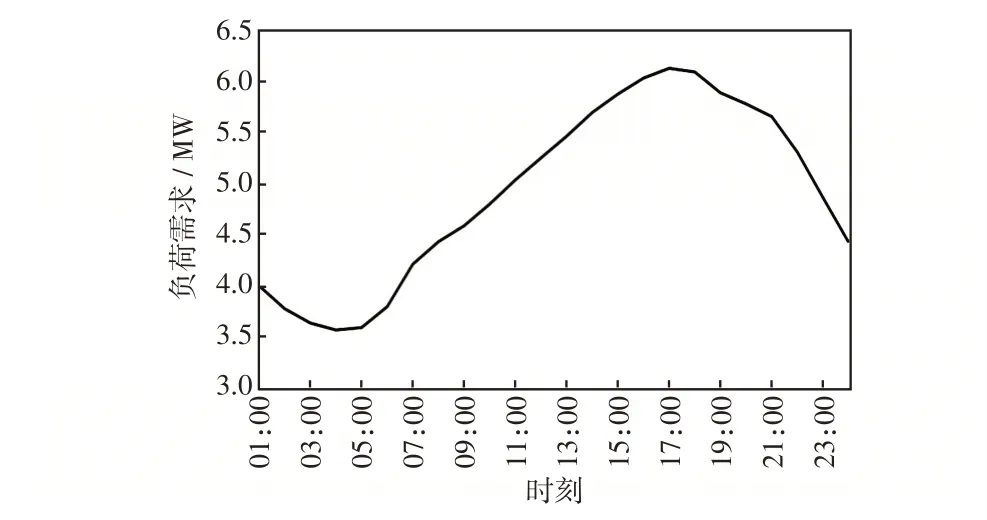
图4 总系统负荷需求Fig.4 Total load demand of system

表1 杆塔故障概率参数Tab.1 Parameters of tower failure probability

表2 DG 参数Tab.2 DG parameters

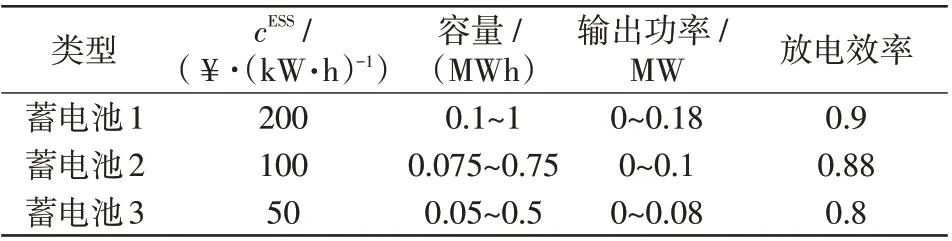
表3 ESS 参数Tab.3 ESS parameters

图5 初始时刻各节点负荷需求和负荷等级Fig.5 Load demand at each node and load levels at the initial moment

4.2 结果与分析

本节设置以下3种场景来进行算例分析。

场景1 假设DG 和ESS 已固定安装在配电网中，仅考虑线路加固策略。

场景2 综合考虑线路加固和DG、ESS 配置的联合优化，但不考虑负荷等级。

场景3 综合考虑线路加固和DG、ESS 配置的联合优化，同时考虑负荷等级，结果与分析如下。

（1）假设系统在遭受极端天气影响下的故障修复时间为6 h，两种类型的台风移动时，配电系统地面风速变化如图6所示，将台风等级设为一级。如果所有杆塔都不采取任何加固策略并且在没有安装DG 和ESS 的情况下，经过本文模型计算得出台风最终会导致线路L2-3、L5-6、L7-8、L2-19、L6-26发生故障，故障规模达到5 重。DG、ESS 布点位置和系统损坏情况如图7 所示，虚线为故障线路，虚框为系统故障区域。故障共造成23.676（MW·h）的切负荷量，总计228 240¥的经济损失。

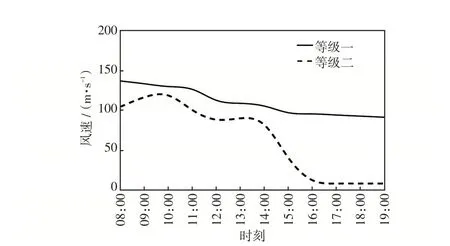
图6 台风的等级风速Fig.6 Wind speed of different levels under typhoon weather

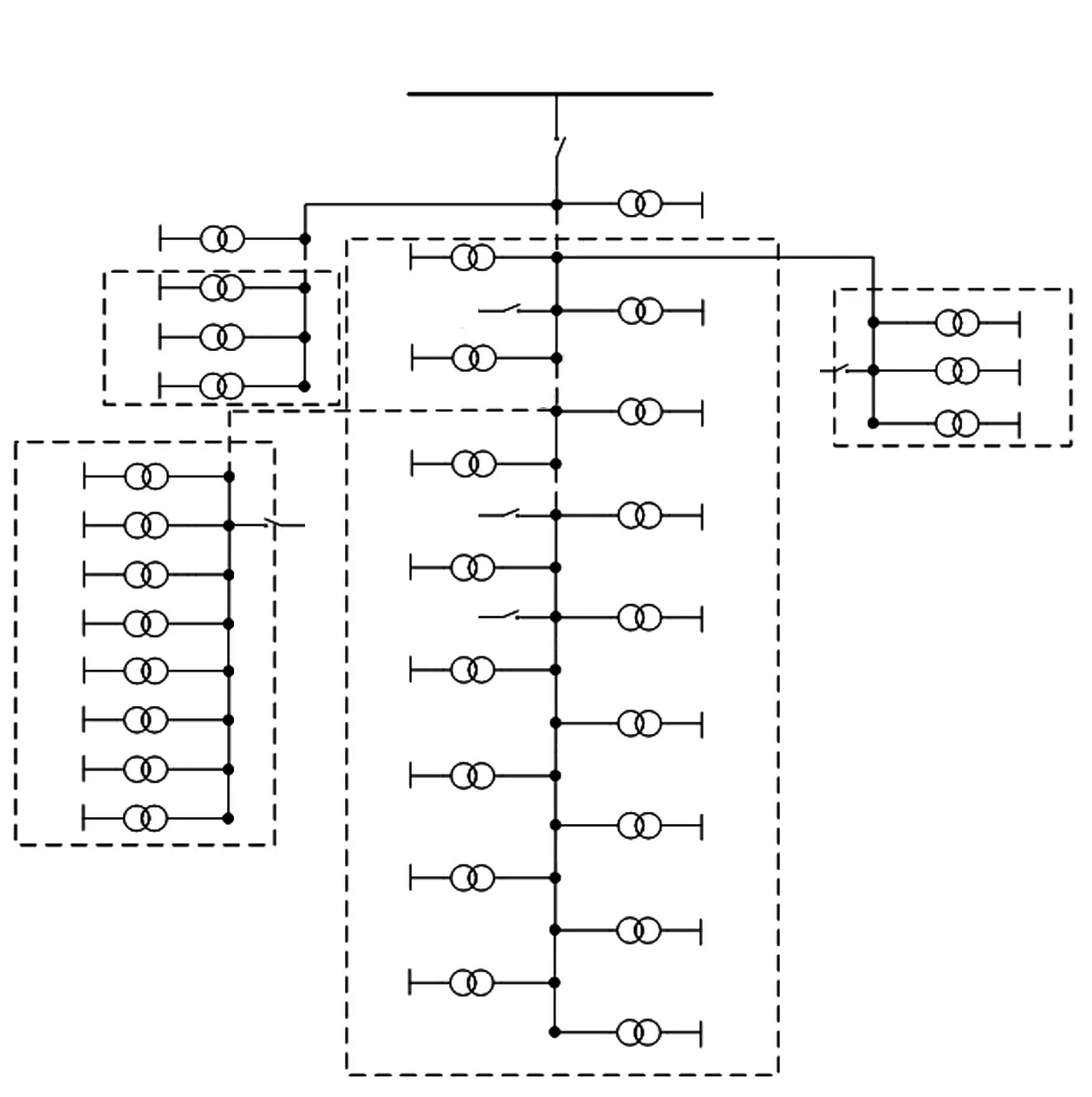
图7 系统未加固时线路毁坏情况Fig.7 Line damages when the system is not reinforced

（2）为防止出现如图7 所示的大规模切负荷的情况，采用场景1策略，即通过3阶段模型求解出最优加固线路，加固方案如表4所示。在每次的迭代过程中，选择1条故障后带来损失最大的线路进行加固，同时更新故障线路信息。例如，在第1 次迭代中，对线路L2-3进行了加固，因为一旦L2-3发生了故障，使得功率无法流向下游节点，将对系统造成严重的切负荷成本。在对系统进行共4 次线路加固之后，线路加固成本控制在总预算范围内。切负荷成本最终降低至85 060 元，降幅达到62.7%，“最坏情况”下故障线路为L9-10、L3-23。

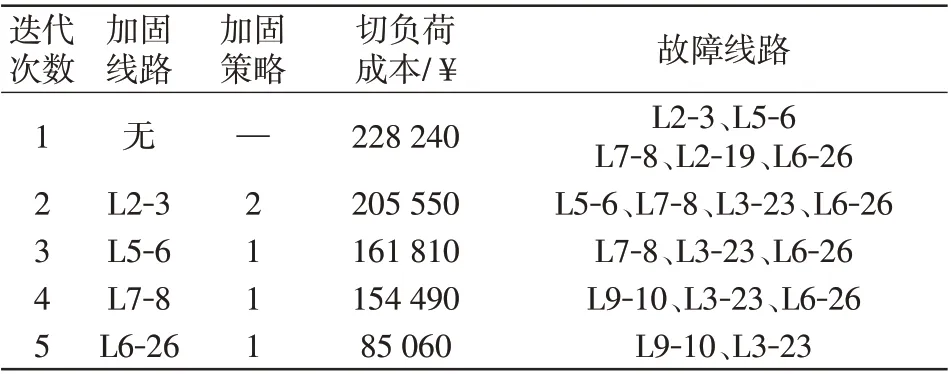
表4 场景1 中最佳线路加固方案Tab.4 Optimal scheme for line reinforcement in Scenario 1

（3）在仅考虑加固杆塔的措施下，切负荷成本会得到大幅度降低，但在4 次加固线路之后，系统仍然无法完全抵御极端天气的灾害，线路L9-10、L3-23仍会发生故障，导致下游负荷点10-18、23-25中的负荷失去供电，而此时故障区域内仅有3 台ESS 设备，其余DG 难以发挥对失电负荷的支撑作用。为此，考虑利用场景2 的策略，即采取综合考虑线路加固和DG，ESS 配置的联合优化，暂时不考虑负荷等级。所求最佳电源安装方案如表5所示。

表5 场景2 中DG，ESS 配置方案Tab.5 Deployment scheme for DG and ESS in Scenario 2

由于对DG/ESS的布点位置是根据故障区域而定，场景2 中的切负荷成本获得进一步降低，说明联合优化对韧性提升有着显著作用。故障区域内各节点的切负荷量如图8所示，白色柱块为该节点的切负荷量。由于场景2 中未对负荷重要性加以区分，导致分布式电源对故障区域内负荷的供电支撑没有针对性，甚至出现了对一级负荷完全不供电的情况。

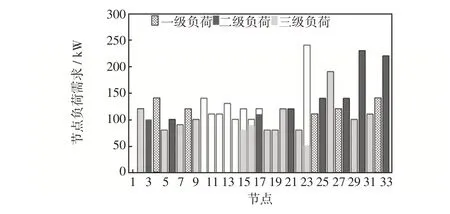
图8 场景2 中各节点切负荷量情况Fig.8 Load shedding at each node in Scenario 2

（4）由于节点10-18、23-25中的一、二级负荷占比较高。场景2 中的加固模式虽然可以进一步降低系统的切负荷成本，但对重要负荷的抗灾能力提升效果并不明显。为进一步提升系统韧性，减少关键节点的切负荷量，采用场景3 中的策略，即考虑负荷等级的基础上，综合考虑线路加固和DG，ESS 配置的联合优化，为可能面临断电风险的关键负荷提供供电支撑。所求最佳电源安装方案如表6所示。

表6 场景3 中DG，ESS 配置方案Tab.6 Deployment scheme for DG and ESS in Scenario 3

在场景3的加固策略中，最终的DG和ESS的安装位置以及线路毁坏情况如图9 所示。图中已标明加固线路和相应的加固策略。故障区域内各节点的切负荷量如图10所示。

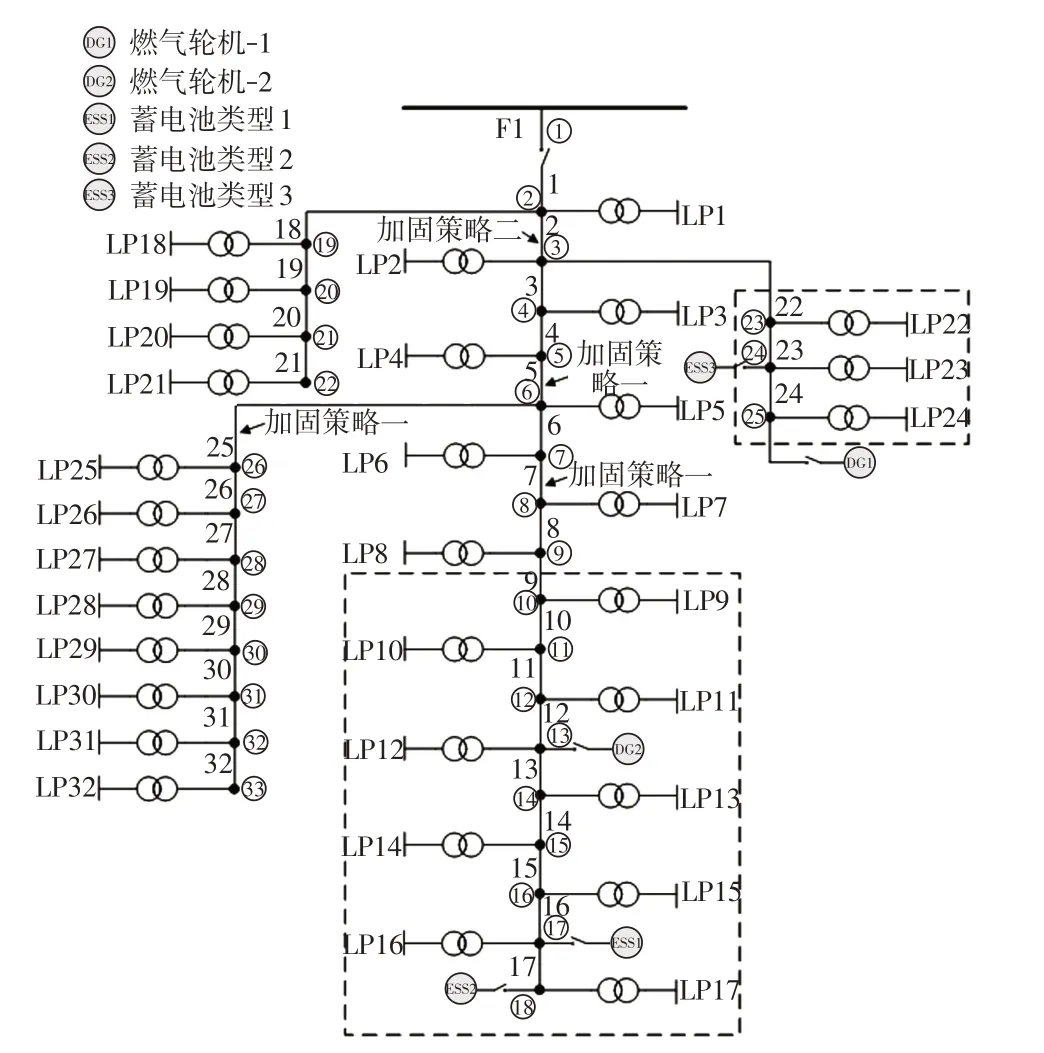
图9 场景3 电源安装位置和线路损坏情况Fig.9 Power supply deployment position and line damages in Scenario 3

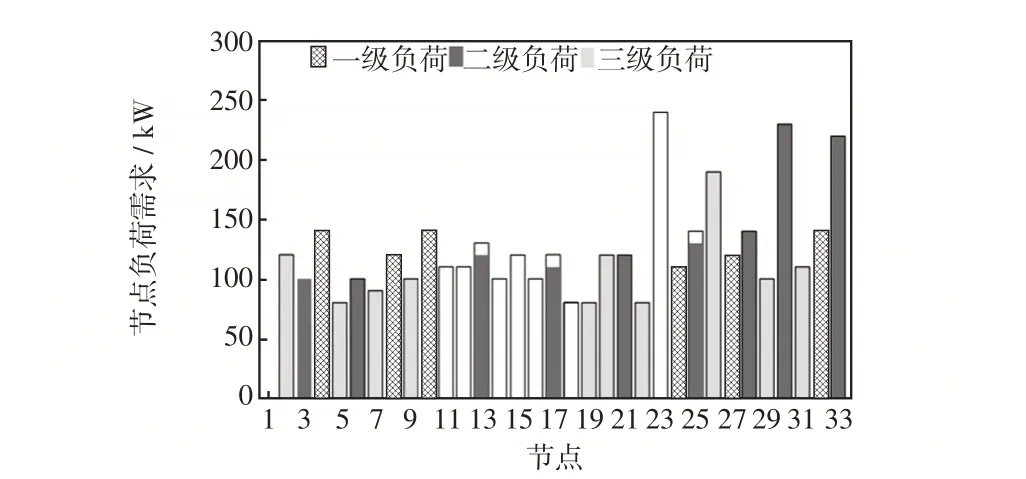
图10 场景3 中各节点切负荷量情况Fig.10 Load shedding at each node in Scenario 3

由于考虑了负荷的重要性，使在故障区域内的一级负荷节点10 和24 得到了供电支撑，在保证对所有一级负荷的供电之后，选择支撑相对重要的二级负荷，而把在故障区域内的三级负荷则全部切除。在场景3 中，最终可以将切负荷成本降低至41 110 元，投资总费用为122 610 元。在投资成本相同的情况下，场景3 较场景2 的切负荷成本进一步降低，降幅达到37.1%，说明了对故障区域内关键负荷的供电支撑可以显著提升系统韧性。

4.3 灵敏度分析

为说明投资预算和台风等级对系统韧性的影响，本文分析了加固投资预算和台风等级对系统切负荷成本的影响，并假设系统本身未进行线路加固和DG/ESS 布点配置，计算结果如图11 所示。对于所有等级的台风，切负荷成本会随着投资预算的增加而相应地减少。同时，更严重的台风天气会带来更大的切负荷成本及更高的加固投资成本。

图11 不同投资预算和台风等级下的切负荷成本Fig.11 Load shedding cost under different investment budgets and different typhoon levels

5 结 语

本文提出了一种通过事前加固杆塔和安装DG以及ESS 的方式来提升配电系统韧性的方法。将该问题建模为3阶段优化问题，进而将模型转变为双层模型求解，第1 层求解了升级杆塔和安装DG以及ESS 的策略，第2 层模拟配电系统在“最坏情况”下的最小化切负荷成本。在求解方面，将第2和第3 阶段的模型通过对偶理论和线性化理论转换成单段模型，进而设计迭代算法求解整体模型。最后在改进的IEEE 33节点测试系统上进行了算例分析，结果表明，所提模型和算法可以帮助配电公司制定最优电网加固策略和DG 布置方案，以减轻配电系统在极端天气中的经济损失。