柔性直流配电网的静态运行域初探

肖 峻，莫少雄，秋泽楷

（天津大学智能电网教育部重点实验室，天津 300072）

近年来，配电网“源荷”的直流特征日益明显，相比于交流配电网，直流配电网更利于光伏等直流电源及电动汽车等直流负荷的接入。另一方面，城市用电负荷日益密集，交流配电网面临线路走廊紧缺、供电容量扩展受限的问题[1]，而直流配电网能有效提高供电容量[2]。在此背景下，基于电压源换流器VSC（voltage source converter）的柔性直流配电网（简称柔直网）成为研究热点[1，3，4]，并已在城区、工业园区、大学校区建成示范工程[5]。

安全性是配电网运行的基本要求。目前，国内外学者多从控制策略优化角度提高柔直网安全性。文献[6]提出了柔直网分层协调控制架构，可兼顾运行成本与电压越限概率，维持直流电压稳定，实现源荷设备依序按可调功率裕度之比出力；文献[7]提出了考虑功率裕度并附加定直流电压控制的柔直网自组织下垂控制优化方案，可降低换流站过载风险，实现电压无差调节。在调度方面，文献[8]提出了反映柔直网下垂控制下功率和电压平衡状态的指标，为柔直网实时调度提供安全性判据；文献[9]提出了柔直网双时间尺度调度策略以平衡经济效益与安全性，其安全性是通过优化下垂系数改善电压分布、考虑控制器对不平衡功率响应来实现。上述文献均未确定柔直网调度运行边界，难以获得柔直网整体安全性测度与工作点安全裕度，不利于实现柔直网安全态势感知[10]和预防控制[11]。

域是系统在给定约束下的最大允许运行范围[12]，确定域是研究系统的基本问题。确定域后，可根据工作点是否在域内判断系统状态是否安全，并采取预防控制措施[11]，提高安全裕度。准确刻画域边界后，调度员才可将系统运行于接近边界的高效区域，从而提高系统效率。有学者针对交流配电网，提出了配电安全域DSSR（distribution system se⁃curity region）的概念和方法[12]，并形成理论体系[10-14]，其方法体现出速度快、可观测、安全信息丰富的优势[13]。DSSR 的概念和方法还扩展到舰船直流系统[15]与综合能源系统[16]。

目前，DSSR 研究主要基于N-1 安全准则，但在配电网运行的大部分时间，N-1事件概率不高，即使工作点越出N-1边界，当满足正常运行时的安全约束，配电网仍可正常运行，调度员既可采取预防控制措施，也可暂时观察不采取措施，但前提是清晰界定正常运行范围，即运行域。文献[17]提出了主动配电网中分布式电源和微网运行域的概念、模型与算法。文献[18]提出了三相不平衡配电网的分布式电源运行域仿射求解算法，运算速度较文献[17]有所提高。上述研究均采用仿真法，未得到域表达式，难以反映运行域完整边界。文献[14]建立了交流配电网运行域模型，采用解析法求得能反映运行域完整边界的域表达式。

由于柔直网具有最大允许运行范围，通过对运行域的研究能刻画出柔直网的调度运行边界。对于柔直网存在的动态稳定问题[6，7]，其运行域的研究需分静态和动态两步进行，本文只研究了其静态运行域。目前，现有交流配电网运行域模型不再适用柔直网，因此，本文提出了柔性直流配电网的静态运行域模型。首先讨论网络接线模式与稳态运行特性，然后给出静态运行域模型与求解方法，最后采用算例在不同控制策略下进行了验证与分析。

1 接线模式与稳态运行特性

1.1 柔直网接线模式

柔直网的接线模式有辐射状、单联络、环状、三端互联等[2，5]，其中单联络接线能兼顾可靠性与经济性，获得更多青睐。单联络柔直网示意如图1 所示，两端交流系统经换流站VSC1、VSC2连接到中压直流母线，再向馈线输送直流电。直流断路器将馈线分隔为n+1个馈线段，形成n个节点，各节点通过DC-DC或DC-AC适配器（图中未画出）连接直流或交流负荷。

图1 单联络柔直网Fig.1 Single-connection flexible DC distribution network

1.2 柔直网闭环运行方式

在柔直网中，因VSC具有抑制故障电流的限幅控制环节[19]，且不存在无功环流，故一般采取闭环运行方式。某一负荷由多个电源供电，当负荷失去某一电源供电时，其余电源会主动做出功率支援，无需开关倒闸操作。

1.3 柔直网潮流控制策略

柔直网具有潮流连续调控能力，其控制装置主要为VSC。柔直网的典型潮流控制策略有主从控制、电压裕度控制和下垂控制[3，4]。

主从控制设置一主换流站VSC0，其直流电压给定，有功功率可为容量范围内任意值；其余从换流站VSCk均给定有功功率，直流电压为安全电压范围内任意值。各换流站直流电压与有功功率的关系可表示为

式中：UVSC0、UVSC0,ref分别为主换流站的实际电压与电压参考值；PVSCk、PVSCk,ref分别为从换流站的实际功率与功率参考值；N为从换流站数量。

电压裕度控制是在主从控制基础上，在从换流站中设置一台加装电压偏差控制器的备用换流站VSCn，当其电压在设定范围内时采用定有功功率模式，当其电压达到设定的裕度上、下限时切换至定直流电压模式。各换流站直流电压与有功功率的关系可表示为

式中：PVSCn、PVSCn,ref分别为备用换流站实际功率与功率参考值；UVSCn、UrefH和UrefL分别为备用换流站的实际电压、电压裕度上限和下限。

下垂控制利用给定的各换流站直流电压与有功功率的斜率关系，实现多点直流电压控制以及有功功率在各换流站间的自动分配。各换流站直流电压与有功功率的关系可表示为

式中：UVSCk、UVSCk,ref分别为换流站VSCk实际电压与电压参考值；PVSCk、PVSCk,ref分别为换流站VSCk实际功率与功率参考值；Kk为换流站VSCk下垂系数。满足式（3）的节点被称之为下垂节点。

2 静态运行域模型与求解方法

2.1 交流配电网静态运行域模型

静态运行域是系统正常运行时满足各稳态安全约束的工作点集合[17]。其中，工作点是能唯一完整描述系统状态的一组独立变量，安全分析中选取负荷功率构成工作点[12]。交流配电网的静态运行域模型[14]可表示为

式中：ΩDR为运行域；W为由负荷视在功率Si构成的工作点；Θ为工作点定义域；Ui为节点i的电压幅值；θij为节点i和节点j的电压相角差；gij、bij分别为节点i和节点j间的电导和电纳；ṠBm,r、CBm,r分别为第m号馈线的第r段复功率与容量；Ω(Bm,r)为馈线段Bm,r下游负荷节点集合；Ploss、Qloss分别为馈线段Bm,r及其下游线路的有功和无功损耗；ṠTk、CTk分别为第k号主变复功率与容量；ṠBm,1为第m号馈线出口复功率；Ω(Tk)为所有由第k号主变引出的馈线集合。

式（5）～（6）为潮流方程；式（7）～（8）为馈线段和主变容量约束；式（9）为节点电压约束。式（4）～（9）模型不适用于柔直网，原因如下。

（1）式（4）～（9）模型针对开环运行的交流配电网，每处负荷都从单一电源经单一路径获取电能，由式（7）得到各馈线段功率等于下游负荷功率与网损之和；但闭环运行时，负荷可从多个电源经多个路径获取电能，各馈线段功率不能仅用下游负荷表示，因此，当柔直网闭环运行时，由式（7）无法计算各馈线段功率。

（2）柔直网改变了传统交流配电网潮流的自然分布。式（4）～（9）模型缺少潮流控制策略对应的约束，故不适用于柔直网。

综上，交流配电网运行域模型不适用于柔直网。此外，舰船直流系统的域模型[15]是针对舰船直流系统特定结构与开环运行方式，也不适用柔直网。

2.2 柔直网静态运行域模型

柔直网的静态运行域模型可表示为

式中：ΩDR为运行域；W为由负荷有功功率构成的工作点；Θ为工作点定义域；Pi、Ui分别为节点i的净注入功率和直流电压；Gij为节点i、j间的互电导，j∈i表示所有和i相连的节点j（含j=i）；Pij、CBij分别为节点i、j之间馈线段Bij的功率和容量；CVSCk、UVSCk、PVSCk分别为换流站VSCk的容量、直流电压和注入柔直网的功率；fk(PVSCk,UVSCk)=0 为VSCk电压与功率关系式；Ui,max、Ui,min分别为节点i允许的最高和最低电压。

式（11）为潮流方程；式（12）为馈线段容量约束；式（13）为节点电压约束；式（14）为换流站容量约束，因连接柔直网的主网可视为无穷大电源[20]，所以未考虑换流站交流侧约束；式（15）为换流站直流电压与有功功率关系约束。

式（10）～（15）柔直网模型与式（4）～（9）交流配电网模型的区别是：式（12）中馈线段功率采用由潮流计算得出的节点电压及节点电导表示，式（7）中馈线段功率直接用其下游所带负荷表示；柔直网模型相比交流配电网模型还增加了对换流站直流电压与有功功率关系的约束，即式（15）。

式（10）～（15）模型能适用于柔直网，是因为该模型兼顾了柔直网的闭环运行能力与潮流控制策略。其中，式（12）的馈线段功率由节点电压及节点电导表示，对于开环和闭环均适用；式（15）能够表示不同换流站的节点类型，该约束可在主从控制和电压裕度控制时提供主换流站电压、从换流站功率等已知量，在下垂控制时，将潮流方程与该约束联立求解。

2.3 模型求解方法

在求解交流配电网运行域及安全域时，为获得完整的域边界，常采用解析法求出域表达式[11-14]。求解过程中因潮流方程的非线性，难以得到显式解析解，故一般基于直流潮流线性化[11-14]。

本文也采用解析法求解柔直网运行域。与交流配电网类似，柔直网潮流方程式（11）也是非线性的，需要线性化才能求得域表达式。为此，本文采用柔直网的DistFlow 支路潮流线性化法[21]，在计算电压降时，用额定电压代替实际电压，将式（10）～（15）模型化为关于负荷功率的线性不等式组，求解得到域表达式，最后近似计及网损，具体步骤如下。

步骤1 检查网络并解环。检查柔直网是否含环网，若无环网，直接执行下一步；若含环网，则从定直流电压节点或下垂节点解环，形成与解环点电压相同的无环网络。

步骤2 获取馈线段功率表达式。根据Dist⁃Flow 支路潮流线性化法，获取的馈线段功率PBk关于节点净流出功率Pj的线性表达式为

式中：φ(Bk,Bn)为馈线段Bk与末端馈线段Bn之间节点集合；Pj为负荷功率，在下垂控制下含有下垂节点功率；PBn为末端馈线段Bn的功率。

步骤3 获取负荷节点电压表达式。根据Dist⁃Flow 支路潮流线性化法，以定直流电压方式或电压-有功下垂方式的换流站电压UVSCm为基准，用额定电压UN、馈线段电阻RBi和步骤2求得的馈线段功率PBi来计算电压降，负荷节点电压Uk关于各节点功率的线性表达式为

步骤4 处理下垂节点。在主从控制和电压裕度控制时，无下垂节点，直接执行下一步。在下垂控制时，将式（3）所示换流站电压-有功下垂关系式与线性化潮流方程联立求解后，将步骤2 和步骤3已获取表达式中的下垂节点功率和下垂节点电压用关于负荷功率的线性化表达式表示。

步骤5 考虑换流站运行方式切换。主从控制和下垂控制时，换流站运行方式不切换，执行下一步；在电压裕度控制时，备用换流站在定直流电压方式和定有功功率方式之间切换，根据换流站节点类型变化情况，重复步骤1～4，求出换流站所有运行方式下馈线段功率和负荷节点电压表达式。

步骤6 求出域表达式。使由负荷功率线性表示的馈线段功率、换流站功率及节点电压满足正常运行时安全约束，形成关于负荷功率的线性不等式组，并将换流站所有运行方式下的结果取并集，得到某一控制策略下静态运行域表达式。

步骤7 考虑网损修正域表达式。由于不同的运行域边界点网损不同，本文用网损最大与网损最小点的偏差率平均值eˉ来近似表示全体边界点的偏差率，用于修正域表达式中的容量约束，使边界向内平移eˉ，从而近似计及了网损。

3 算例分析

3.1 算例概况

单联络柔直网算例如图2 所示。设馈线总长为6 km，馈线容量为8.028 MW，各馈线段电阻均为R= 0.469 2 Ω。换流站容量CVSC1=CVSC2= 10 MW。主从和电压裕度控制下主站VSC1电压取额定电压UN=10 kV；电压裕度控制下VSC2电压裕度取±5%UN；下垂控制下2 个换流站控制参数均相同，直流电压参考值Udc,ref=10 kV，有功功率参考值Pref=4 MW，下垂系数K=0.1。负荷电压允许范围取[0.9UN，1.05UN]。

图2 算例电网结构Fig.2 Structure of grid network in a numerical example

3.2 静态运行域计算

采用本文模型与求解方法计算柔直网在典型控制策略下的静态运行域，以下垂控制为例，给出计算过程，其他控制策略的计算过程见附录A。

3.2.1 计算过程

步骤1 本算例不含环网，直接执行下一步。步骤2 获取馈线段功率表达式，即

步骤4 将换流站电压-有功下垂关系式与线性化潮流方程联立，即

式（20）的前两个等式是本文模型中式（15）针对下垂控制的具体化，体现了换流站直流电压与有功功率需要满足的下垂关系，而交流配电网静态运行域模型无法体现此下垂关系。对式（20）求解可得

将K= 0.1，R= 0.469 2 Ω，UN= 10 kV 代入式（21），根据换流站电压-有功下垂关系，得到VSC1功率和电压关于负荷功率的线性表达式为

步骤5 下垂控制下换流站运行方式不做切换，执行下一步。

步骤6 将式（22）代入式（18）、式（19），得到由负荷功率表示的馈线段功率、换流站功率、节点电压，使这些物理量满足正常运行时的安全约束，形成关于负荷功率的线性不等式组，即

步骤7 网损修正。网损最小和最大边界点分别为（7.699 7，7.699 7）和（0，13.437 9），求解过程见附录B。网损最小点与式（24）对应边界点（8.028，8.028）偏差4.09%，网损最大点与式（24）对应边界点（0，14.112 8）偏差4.78%，两偏差平均值为4.44%。将式（24）边界向内平移4.44%，得到近似计及网损后的域表达式，即

3.2.2 计算结果

不同控制策略下柔直网静态运行域表达式见表1。

表1 算例中柔直网静态运行域表达式Tab.1 Expressions of static dispatchable region of flexible DC distribution network in the example

3.2.3 误差分析

在本文模型求解中进行了近似线性化处理。为分析所得运行域边界的误差，先通过潮流计算得到精确边界点，再将求出的精确边界点P1值代入表1中的域表达式，求出对应有相同P1值的近似边界点，精确边界点与近似边界点的误差可表示为

式中：（a，b）为修正后近似边界点；（a，c）为与P1值相同的精确边界点。

边界点最大误差见表2，详细数据见附录表C1。

表2 算例中柔直网静态运行域边界点误差Tab.2 Errors at boundary points of static dispatchable region of flexible DC distribution network in the example

由表2可知，本算例（馈线总长6 km）运行域边界点误差较小。误差源于求解方法对网损的近似，网损与馈线长度正相关。目前柔直网应用的城区、工业园区、大学校区的馈线长度不大于6 km，因此本文求解方法能满足目前实际柔直网的精度要求。

3.3 不同控制策略下分析

可视化是研究域的常用手段[15-18]，故通过可视化比较不同控制策略下静态运行域。柔直网一般闭环运行，闭环运行时只有节点功率能反映负荷大小，馈线出口功率不能反映负荷大小。因此，在柔直网运行域可视化时，一般选取节点功率为观测变量。以节点功率P1、P2为观测变量的可视化静态运行域如图3所示。

图3 典型控制策略下柔直网可视化静态运行域Fig.3 Visualized static dispatchable region of flexible DC distribution network under typical control strategies

由图3可得如下规律。

规律1 主从控制和电压裕度控制下的静态运行域大小相同，其主要是因为电压裕度控制下柔直网有两种正常运行状态。

在状态1 下，VSC2电压在裕度内且给定有功功率，安全约束与主从控制的唯一区别是增加对VSC2电压范围的限制，由附录式（A7）结果可知，在特定VSC2功率下负荷允许范围较主从控制时变小，但当VSC2功率在全范围内可调时，负荷允许范围与主从控制相同。

在状态2 下，线路压降过大使VSC2进入定直流电压模式，VSC2电压钳制在设定的上限或下限，其功率不再可控，馈线段功率同时受馈线段电阻和2 个换流站电压差影响，使该状态下负荷允许范围较状态1 缩小，见附录式（A8）～（A9）。在状态2 中负荷允许范围缩小，但静态运行域是所有正常运行状态中的负荷允许范围，因此对上述两种状态中的负荷允许范围取并集后，电压裕度控制的静态运行域与主从控制大小相等。

规律2 主从和电压裕度控制下静态运行域大于下垂控制下静态运行域。其主要原因是在下垂控制下，由式（21）分析可知换流站功率与负荷功率间存在一定牵制关系，换流站功率不能独立调控；然而在主从控制和电压裕度控制下，从换流站功率可以独立调控，与负荷功率间无牵制关系，静态运行域约束和下垂控制相比，减少了与换流站数量相同的等式约束，因此静态运行域更大。

4 结 语

本文初探了柔性直流配电网的静态运行域，提出柔性直流配电网的静态运行域模型及其解析化求解方法，有效刻画了柔性直流配电网正常运行时的最大允许范围。误差分析结果表明，本文模型与求解方法能满足目前实际柔性直流配电网的精度要求。

本文模型与求解方法能适用于主从控制、电压裕度控制、下垂控制三种典型控制策略。研究发现主从控制和电压裕度控制的静态运行域大小相同，均大于下垂控制的静态运行域。

后续将研究N-1安全域，考虑稳定问题，扩展到LCC-VSC混合直流配电网与交直流混联配电网。

附录A 其他控制策略下静态运行域计算

A1 主从控制下静态运行域计算正文算例柔直网在主从控制下安全约束可表示为

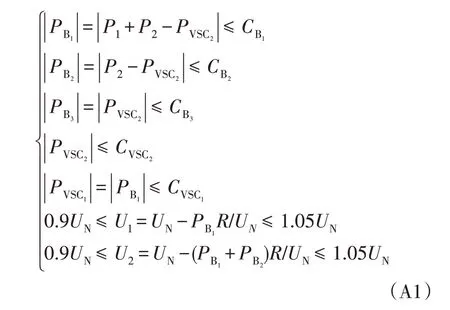
式中：主换流站电压为额定电压UN；从换流站功率PVSC2为可控量，这是模型式（15）对主从控制的具体化。

馈线段容量CB1=CB2=CB3=8.028 MW，换流站容量CVSC1=CVSC2=10 MW，额定电压UN=10 kV，负荷电压允许范围为[0.9UN,1.05UN]，各馈线段电阻R均为0.469 2 Ω。将数据代入附录式（A1），剔除无效约束，PVSC2取值范围为[-8.028，8.028]，则静态运行域表达式为

根据网损对附录式（A2）进行修正。潮流计算可得网损最小边界点为（7.725 6，7.725 6），与附录式（A2）对应边界点（8.028，8.028）偏离3.77%；网损最大边界点为（0，15.125 6），与附录式（A2）对应边界点（0，16.056）偏离5.79%。将附录式（A2）所示边界按偏差平均值4.78%向内平移，则修正后近似考虑网损的静态运行域表达式为

A2 电压裕度控制下静态运行域计算

在电压裕度控制时，备用换流站VSC2电压裕度为±5%UN，当VSC2工作在定有功功率模式且电压在±5%UN内时，柔直网安全约束为

当VSC2工作在定直流电压模式且电压为上限1.05UN时，柔直网安全约束为

当VSC2工作在定直流电压模式且电压为下限0.95UN时，柔直网安全约束为

附录式（A4）～（A6）中，主换流站VSC1电压均为UN。附录式（A4）给定备用换流站功率PVSC2且限定UVSC2在±5%UN内；附录式（A5）给定备用换流站电压1.05UN；附录式（A6）给定备用换流站电压0.95UN。这些均为模型式（15）对电压裕度控制的具体化。

附录式（A4）～（A6）化简后有效约束分别为

式中，PVSC2是在[-8.028，8.028]内的控制变量。

将附录式（A7）～（A9）表示的不同状态下安全约束取并集，代入数据，PVSC2取值范围为[-8.028，8.028]，则柔直网在电压裕度控制下的静态运行域表达式为

根据网损对附录式（A10）进行修正。潮流计算可得网损最小边界点为（7.725 6，7.725 6），与附录式（A10）对应边界点（8.028，8.028）偏离3.77%；网损最大边界点为（0，15.125 6）与附录式（A10）对应边界点（0，16.056）偏离5.79%。将附录式（A10）所示边界按偏差平均值4.78%向内部平移，得到修正后近似考虑网损的静态运行域表达式为

A3 主从和电压裕度控制下网损最小和最大边界点求解

由于主从控制和电压裕度控制下静态运行域边界相同，其对应边界点状态也相同，故统一考虑。

A3.1 网损最小边界点求解

网损最小时潮流具有对称性。图2中，B1和B3功率达上限8.028 MW，产生等量损耗；B2无功率流动，损耗为0；VSC1和VSC2电压均为10 kV，负荷功率为

由此可得网损最小的边界点为（7.725 6，7.725 6）。

A3.2 网损最大边界点求解

网损最大时，某一节点负荷为0，另一节点负荷最大。

1）P1=0，P2最大

边界点为（15.189 1，0）。

3）比较以上2个边界点（0，15.125 6）与（15.189 1，0）的网损大小，因2个边界点下的总注入功率均为8.028×2=16.056 MW，所带负荷15.125 6 MW<15.189 1 MW，故网损最大边界点为（0，15.125 6）。

附录B 下垂控制下网损最小与最大边界点求解

B1 网损最小边界点求解

网损最小时潮流具有对称性。图2中，B1和B3功率达上限值8.028 MW，产生等量损耗；B2无功率流动，损耗为0；2个换流站电压均为[10-0.1（8.028-4）]kV，负荷功率为

B2 网损最大边界点求解

网损最大的边界点产生于某一节点负荷为0且另一节点负荷最大的2个边界点之中，由于下垂控制时VSC1和VSC2控制方式及参数相同，故这两个边界点负荷分布是对称的，只需求其中任一边界点即可。

可求P1=0且P2最大的边界点，此时只有B3功率达上限8.028 MW，各馈线段均产生损耗，VSC2电压为10-0.1（8.028-4）=9.597 2 kV，则负荷P2节点电压为

附录C 静态运行域边界误差计算

各种控制策略，均给出某一精确边界点计算过程，其它边界点计算过程类似，不再赘述。

C1 下垂控制下误差计算

本算例有效约束均为馈线段容量约束，因此计算精确边界点时需令相应馈线段功率达到上限。下垂控制时，对于边界点（P1，P2），若P1P2，则仅馈线段B1功率达到上限；若P1=P2，则馈线段B1和B3功率均达到上限。

当P2=11.525 2 MW时，求出P1允许的最大值即可求出该精确边界点。根据功率平衡可知P1

负荷功率P1、VSC1电压UVSC1、VSC1功率PVSC1满足的方程组为

解得P1=2.615 1 MW，可得精确边界点为（2.615 1，11.525 2）。将精确边界点P1值代入表1中的域表达式，得到对应近似边界点为（2.615 1，11.504 9），由式（26）计算出该近似边界点的误差为

C2 主从和电压裕度控制下误差计算

因主从控制和电压裕度控制下静态运行域边界相同，其对应边界点状态也相同，误差计算一并考虑。

在主从和电压裕度控制时，边界点（P1，P2）、馈线段B1和B3功率均达上限值为8.028 MW。

假设P1=1.287 6 MW，求出P2允许的最大值即可求出该精确边界点。VSC1电压为10 kV，P1节点电压为

负荷P2大小为P2,1+P2,2=6.228 0+7.706 5=13.934 5 MW，此精确边界点为（1.287 6，13.934 5）。

将精确边界点P1值代入表1中的解析式，得对应近似边界点（1.287 6，14.001 4）。由式（26）算得误差为

按上述方法可求出多个精确边界点、近似边界点及其误差，三种典型控制策略下的域边界点误差见附录表C1。

表C1 典型控制策略下柔直网静态运行域边界点误差Tab.C1 Errors at boundary points of static dispatchable region of flexible DC distribution network under typical control strategies