整体温度变化下钢管混凝土拱桥结构效应分析

汪继文，潘兴虎，叶惠忠，周愉涛，卢彭真

(1.金华市交通工程管理中心 金华市 321001； 2.浦江县交通集团投资公司 金华市 322200；3.杭州市临安区公路服务中心 杭州市 311300； 4.浙江工业大学 土木工程学院 杭州市 310014)

0 引言

桥梁结构长期暴露在自然环境中，受到复杂多变气候条件的影响，在日照、骤然升降温、年温变化等温度荷载的作用下会产生温度应力[1]。桥梁结构的温度应力，实际上是一种约束应力，即结构由于温度变化产生的变形受到约束时所产生的应力。国内对混凝土桥梁的温度效应已进行了较为深入研究[2-5]。但目前相关的一些研究主要是以铁路桥、混凝土箱形梁桥、连续梁桥等为研究对象或仅选取某一结构的构件进行分析，而对于钢管混凝土拱桥这种新兴桥型的研究依旧较少。如，钟善桐[6]对单根柱进行了研究，陈宝春等[7]在此基础上结合所观测的实桥，编写了计算程序以指导设计与施工。针对上述问题，根据陈宝春等[8-10]在钢管混凝土拱桥温度效应方面的研究，以永宁江2号大桥为例，将等效时变的温度效应模型融入到钢管拱桥空间有限元模型中，计算了该钢管混凝土拱桥在温度作用下的位移及内力值，得到了在整体升降温温度荷载作用下钢管混凝土拱桥结构温度内力的变化规律，为今后在设计和计算同类型桥梁，尤其是在温差变幅较大的地区，修建该种结构的桥梁提供依据和参考。

1 工程概况及有限元模型建立

永宁江2号大桥B主桥为飞鸟式钢管混凝土拱桥，跨径布置为(30+80+30)m，主桥中心桩号为K2+422.0，桥梁全宽64.6m，左右分幅，单幅桥桥面宽32.2m。主桥立面、横断面如图1、图2所示。

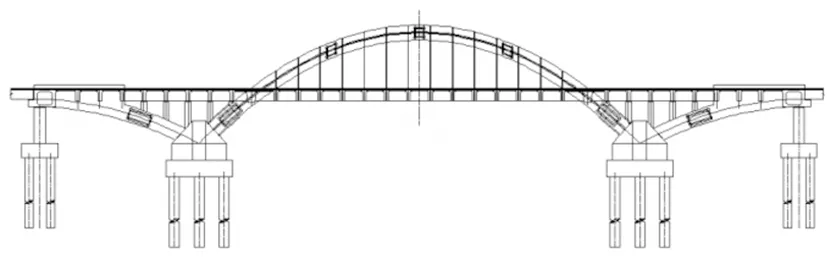
图1 主桥立面示意图

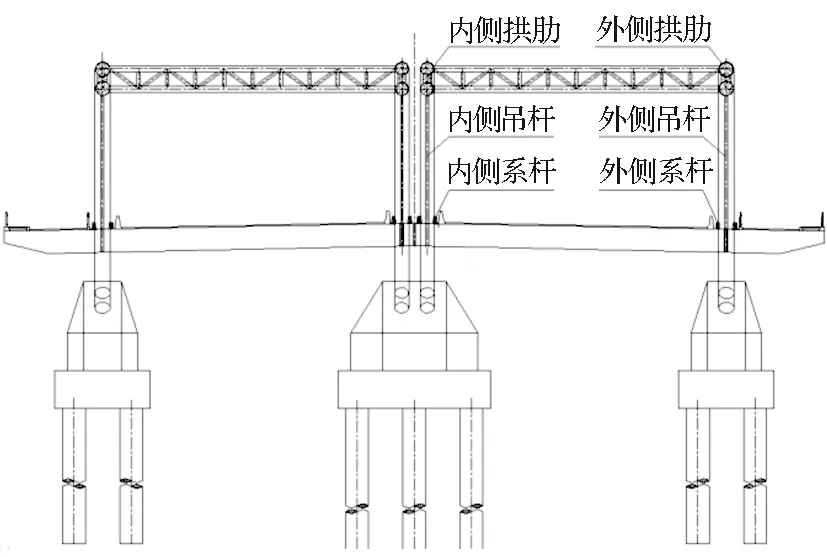
图2 主桥横断面示意图

采用ANSYS15.0建立了全桥有限元模型，对其拱肋核心混凝土进行了变形和应力模拟计算。主拱肋弦管采用哑铃型截面。在借鉴了以往钢管混凝土拱桥有限元建模后[11-12]，本研究以Beam188空间梁单元来模拟主拱肋钢管及混凝土、横梁、纵梁、风撑、立柱等结构，采用link8单元模拟系杆和吊杆，采用combine14模拟立柱和横梁。其中，钢管和混凝土单元采用共节点的形式建立，全桥模型见图3。

(a)视角1

2 温度效应理论计算

采用因温度降低而引起的材料收缩来等效混凝土收缩，其中温度产生的应变为：

εT=αCΔT

(1)

式中，αC为膨胀系数；ΔT=T0-T为温度变化，假设T0=17°。

而收缩徐变效应计算分析采用文献[8]中的CEB-FIP(MC90)模型。该模型定义的收缩应变公式如下:

εCS(t,ts)=εCSOβs(t-ts)

(2)

εCSO=εSβRH(fcm)

(3)

εS(fcm)=[160+10βSC(9-fcm/fcmo)]·10-6

(4)

βRH=1.55[1-(RH/RH0)3]

(5)

(6)

式中：εCS(t,ts)—混凝土龄期从ts到t的收缩应变；

ts—收缩开始计算时刻的混凝土龄期(d)；

t—计算所考虑时刻的混凝土龄期(d)；

εCSO—混凝土名义收缩系数；

fcm—混凝土28d龄期时的平均立方体抗压强度(MPa)；

βRH—与年平均相对湿度RH相关的系数，40%≤RH≤90%。

通过考察桥梁所在地区全年的气候条件，设置该钢管混凝土拱桥全年平均湿度RH=80%，年平均气温17℃，最高气温40℃，最低气温-7℃。

根据式(1)～式(6)即可计算得到不同时间收缩应变对应的温度变化。

3 整体温度变化对钢管拱桥挠度的影响

桥梁结构所处环境的温差变化值大小将决定桥梁温度附加内力的大小。一般桥梁结构在计算温度变化影响产生的附加力时，基准温度取结构的合龙温度，假设合龙温度为17℃，考虑五种温度变化(+20℃，+10℃，+0℃，-10℃、-20℃)。自重作用下温度变化对挠度的影响如表1所示。

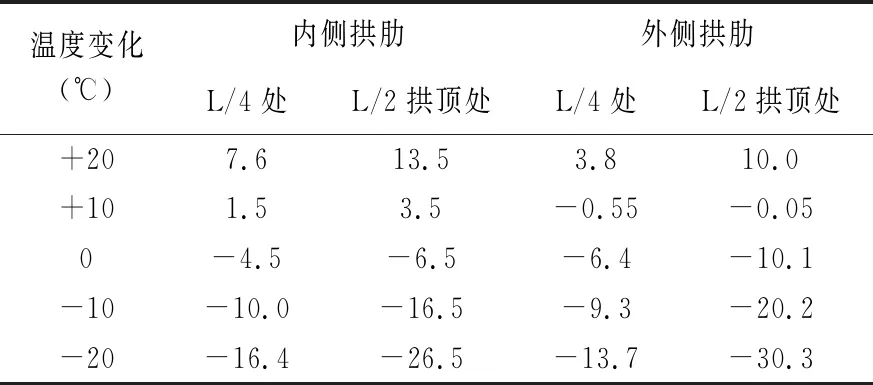
表1 自重作用下温度变化对拱肋挠度影响(mm)

从表1中可以看出，随着温度的升高，拱肋截面挠度由下挠转变为上拱；拱顶截面挠度变化较L/4截面更明显，且分别在外侧拱顶和内侧拱顶达到挠度最大值；当温度由-3℃变到37℃时，内外拱肋拱顶截面挠度分别增加了40mm和40.3mm，内外拱肋L/4截面挠度分别增加了24mm和27.5mm。

4 整体温度变化对结构内力的影响

4.1 整体温度变化对结构轴力的影响

温度变化对控制截面钢管和混凝土轴力的影响如图4所示。

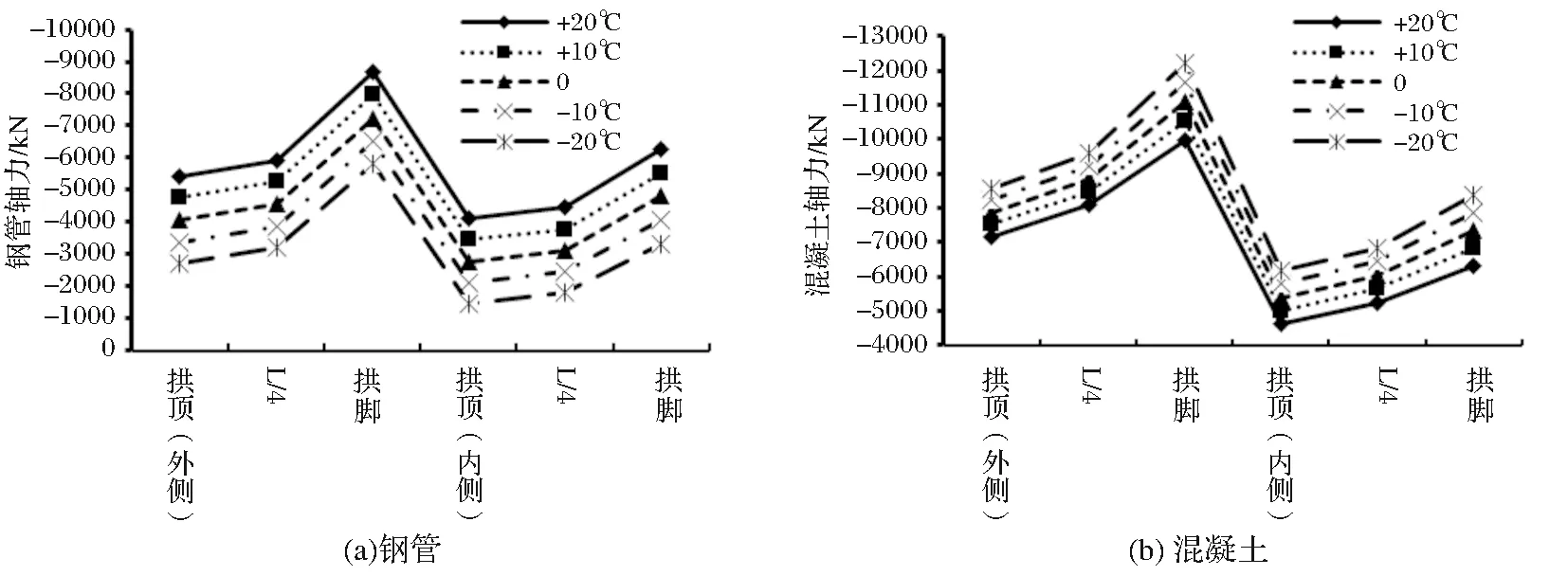
图4 温度变化对控制截面钢管混凝土轴力的影响

从图4中可以看出，随着温度升高，钢管轴力持续增大，混凝土轴力逐渐减小；轴力在拱脚到拱顶方向上呈不断递减的趋势，同时注意到，外侧拱肋轴力均大于同一位置的内侧拱肋的轴力；当温度从-3℃升高到37℃时，内外侧钢管拱脚轴力分别增大了0.90倍和0.50倍，拱顶轴力增大了1.86倍和1.02倍；温度从-3℃变到37℃时，内外侧混凝土拱脚轴力分别减小了25%和18%，拱顶轴力减小了25%和17%。

4.2 整体温度变化对结构弯矩的影响

温度变化对控制截面钢管和混凝土弯矩的影响如图5所示。

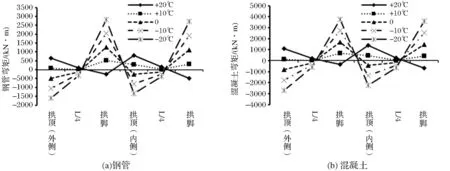
图5 温度变化对控制截面钢管混凝土弯矩的影响

从图5中可以看出，随着温度升高，钢管和混凝土弯矩方向发生变化，其中拱顶处弯矩由负变正，拱脚处弯矩由正转负；拱脚处弯矩小于拱顶弯矩，内侧拱肋弯矩则大于外侧拱肋；当温度从-3℃变到37℃时，内、外侧钢管拱脚处弯矩分别减小了1.18倍和1.09倍，拱顶弯矩增大了1.61倍和1.40倍；而内、外侧混凝土拱脚处弯矩分别减小了1.15倍和1.06倍，拱顶弯矩增大了1.53倍和1.34倍。

5 整体温度变化对结构应力的影响

温度变化对控制截面钢管和混凝土应力的影响如图6所示。

从图6中可以看出，随着温度的升高，拱顶截面应力减小，拱脚截面应力增大；钢管最大压应力为-45.5MPa，最大拉应力为7.7MPa，混凝土全截面受压，最大压应力为-8.8MPa；温度从-3℃变到37℃时，内外侧钢管拱脚应力分别增加了43%和42%，拱顶应力减小了4.53倍和13.44倍；温度从-3℃变到37℃时，内外侧混凝土拱脚应力分别增加了73%和58%，拱顶应力减小了14.5倍和3.1倍。

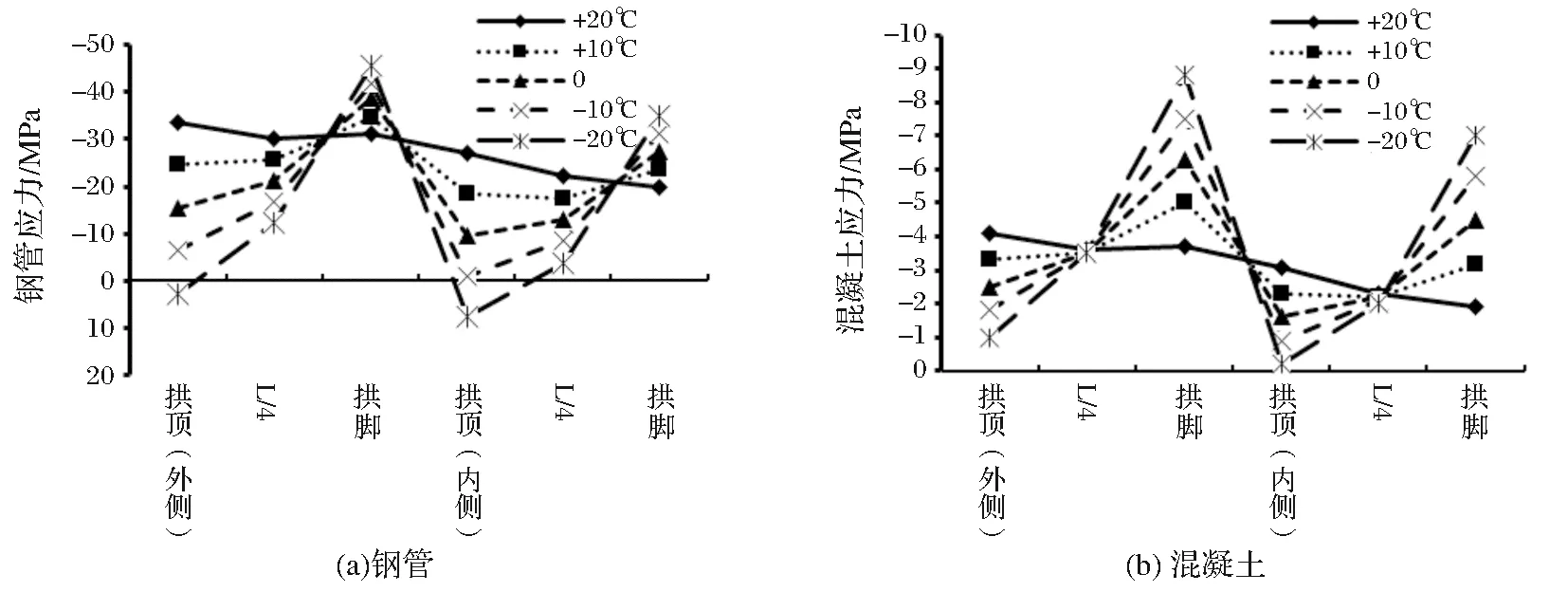
图6 温度变化对控制截面钢管混凝土应力的影响

6 温度荷载对钢管混凝土拱桥稳定性的影响分析

经计算，温度变化对控制截面稳定性的影响如表2所示。

表2 温度变化对稳定系数的影响

从表2中可以看出，随着温度的升高，稳定系数增大，失稳模态均为立柱面外弯曲失稳；稳定系数均大于4，满足设计规范的要求。

7 结论

以跨径布置为30m+80m+30m的某钢管混凝土拱桥为例，融合了等效时变的温度效应模型和有限元方法，建立精确的空间有限元模型，分析了整体温度变化作用下钢管混凝土拱桥的挠度、结构内力和应力以及拱桥稳定性的变化规律，得出了以下结论。

(1)整体温度变化对钢管拱桥挠度影响显著，甚至会出现挠度方向的变化；随着温度升高，钢管轴力增大，混凝土轴力减小；拱脚到拱顶方向上，轴力呈递减趋势；同时钢管和混凝土弯矩方向发生变化，拱顶负弯矩变成正弯矩，拱脚正弯矩变成负弯矩；且拱顶截面应力减小，拱脚截面应力增大，混凝土全截面受压。

(2)当温度由-3℃升至37℃时，内外拱肋拱顶截面、拱肋L/4截面挠度均有所增加；内外侧钢管拱脚、拱顶轴力均增大，内外侧混凝土拱脚、拱顶轴力则减小；内外侧钢管拱脚弯矩减小、应力增加，拱顶弯矩增大、应力减小；内外侧混凝土拱脚弯矩减小、应力增加，拱顶弯矩增大、应力减小。

(3)随着温度升高，稳定系数增大，且稳定系数均大于4，满足要求；失稳模态均为立柱面外弯曲失稳。可见整体温度变化对钢管混凝土拱桥的稳定性影响不大。