湖北省自动土壤水分站容积含水率订正系数阈值探讨
刘银秀,陈 宁,刘 莹,匡晓为
(湖北省气象信息与技术保障中心,武汉 430070)
土壤主要由无机物(45%)、有机物(5%)、空气(12%)和水分(38%)4种成分组成[1]。中国作为农业大国,土壤作为农业生产的最基本生产资料,其水分含量是关键的物理参数,在农作物的水分吸收和养分交换过程中起着至关重要的作用[2,3]。此外,土壤水是联系地表水和地下水的纽带,还能通过改变地表反照率、土壤热容量以及向大气输送潜热和感热等方式对气候变化和生态环境产生影响[4-8]。因此,准确测量和订正土壤水含量具有重要的实际意义和科学价值。
土壤水分的测量方法分为直接法和间接法。直接法即直接测量土壤中的重量含水量和容积含水率,最常见的方法为烘干称重法,测量准确,但耗时长,不具备实时性;间接法则是利用土壤中水分所具有的某些特性来间接推求出土壤含水量,主要包括频域反射测量法(FDR)、时域反射测量法(TDR)、张力计测量法等[9-14]。中国土壤水分自动观测站布设的DZN3型自动土壤水分观测仪采用的是FDR测量技术,该方法具有测量速度快、测量精度高,同一地点下可以连续多次测量且不破坏土壤等优点[15]。但在DZN3型仪器测量值转换为土壤容积含水率终值的过程中,需根据公式Y=A0+A1X进行订正,其中,A0和A12个订正系数由各站点的人工观测资料来确定。由于自动测量仪器与人工观测的原理不同,并且可能存在自动站设备不稳定和人工观测误差等因素,导致订正系数存在一定的不确定性[16]。有研究指出,在进行人工与自动观测的土壤水分对比工作时,当出现土壤水分总的平均绝对误差值偏大时,要分析分层次土壤水分平均绝对误差值是否存在异常,如果分层次有异常,就需要分析相对应的人工土壤水分观测的4个土壤重量含水量是否有异常[17]。研究发现,仪器和人工测量误差是造成江苏省土壤水分观测平均绝对误差值偏大的重要原因。针对土壤水分观测资料的质量控制也开展了许多研究,有学者采用数理统计学方法,分析不同深度人工观测土壤水分资料的历年分布和极值状况,确定各层土壤水分资料的阈值并应用于自动土壤水分观测业务,以提高土壤水分资料的应用价值[18]。张喜英等[19]利用观测数据建立了适合于常德市的土壤水分阈值和质量控制方案。对于特定型号的传感器,有学者采用更加细致的分阶段方法进行标定[20-24]。以往自动土壤水分资料的质控研究中,质控对象主要是订正后的土壤容积含水率及其衍生要素(如土壤相对湿度、重量含水率、有效水分贮存量等),关于土壤容积含水率器测值、标定方程系数质量控制的研究较少。因此,本研究首先对监利土壤水分自动站的归一化频率和容积含水率器测值进行统计分析,进而对容积含水率订正公式中A0和A12个订正系数的取值范围进行了探究。
1 资料与方法
1.1 资料来源
本研究资料来源于湖北省气象信息保障中心,主要为湖北省46个自动土壤水分观测站的气象资料和土壤水分资料。
中国气象局陆面数据同化系统(CLDAS-VI.0)由陆面驱动数据融合和陆面模式模拟两部分组成[25]。基于驱动数据,选取Canrmmity Land Model 3.5(CLM 3.5)作为CLDASVI.0系统的陆面模式进行模拟试验,学者对土壤模拟评估结果较好。为研究需要,利用从国家气象信息保障中心获取的CLDAS 6.25 km网格距5个层次的格点逐小时土壤水分资料,选取2016年7月至2017年12月逐小时CLDAS土壤容积含水率数据,采用水平双线性内插、垂直线性内插的方法,插值到湖北省46个自动土壤水分站点、8个层次。
1.2 观测仪器及数据处理
自动土壤水分观测站逐小时资料包含4个要素,即土壤容积含水率、土壤相对湿度、土壤重量含水率和土壤有效水分贮存量,均为整点小时前土壤测量深度10 cm的平均值。土壤测量深度共有8层,分别为10、20、30、40、50、60、80、100 cm。FDR系列的土壤水分仪利用电磁脉冲原理,根据电磁波在土壤中传播频率来测试土壤的表观介电常数(ε),利用传感器在不同土壤含水量中的SF(归一化频率)变化来得到土壤容积含水率(θv),两者的关系如式(1)所示。

式中,a、b为待定参数;SF为土壤水分传感器采集的信号经处理后的归一化频率。
Sentek公司DZN3型自动土壤水分观测仪出厂时所提供的归一化频率和容积含水率之间的关系如式(2)所示。

式中,A=0.195 7;B=0.404;C=0.028 52。
由式(2)可推导出:

容积含水率仪器测量值与人工测定值呈2次函数关系,通过拟合方程(订正公式),对每一测量层的仪器原始值进行数据订正。订正后如式(4)所示。

式中,X为仪器测量值θv,Y为人工测定值或终值。
根据Taylor中值定理[14],如果函数f(x)在含有x0的某个开区间(a,b)内具有直到(n+1)阶的导数,则对任一X∈(a,b)有:
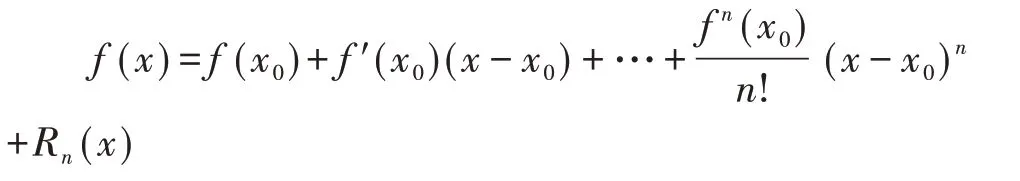
式(4)中,Y相当于f(x),其最高导数的阶数为2阶,故取n=1。
f(x)按(x-x0)的幂展开的带有Peano余项的n阶泰勒公式[14]。
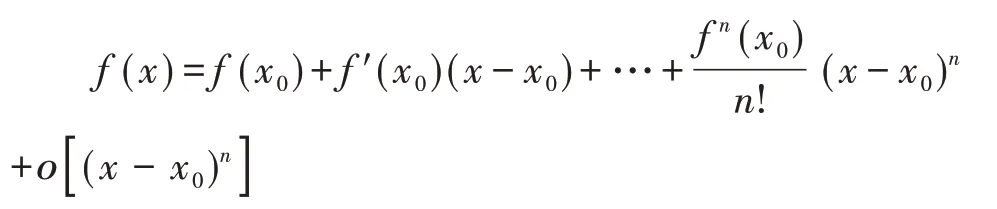
因此有(X-X0)+ο[ (X-X0)],忽略无穷小量,整理得Y≈(B0-B2X02)+(B1+2B2X0)X,实际应用中,令
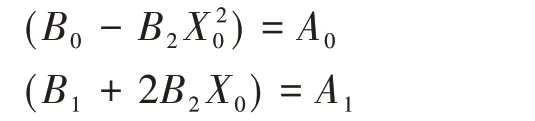
得到实际订正公式(也称标定方程)为:

对湖北省监利站2020年3—4月的观测数据进行研究。以归一化频率、土壤容积含水率订正系数、土壤水分物理系数为原始资料;由式(3)计算器测容积含水率;由式(5)计算容积含水率终值(也称订正后的土壤容积含水率)。用每天20:00的土壤容积含水率资料代表当天土壤容积含水率的日值。
相关数据统计方法如下。
设SF(h,d1)分别表示h厘米、日期d1的归一化频率,SF(h,d2-d1)表示h厘米、日期d2的归一化频率比日期d1的增加值,则有:
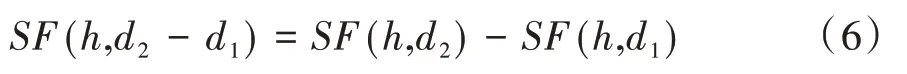
用f(h)表示h厘米、日期d2比日期d1的归一化频率的增加百分比。
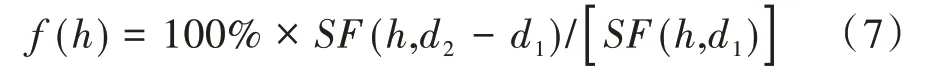
对容积含水率终值的统计方法同式(6)、式(7)。基本统计对象由“归一化频率”变为了“容积含水率终值”。
60 cm容积含水率逐日增值由式(8)求得。
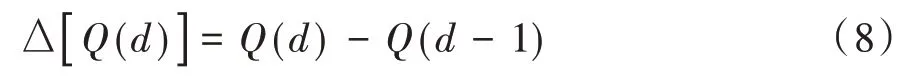
式中,Q(d)代表当日60 cm器测容积含水率;Q(d-1)代表前一日60 cm器测容积含水率,Δ[ ]Q(d)代表当日60 cm器测容积含水率增值。当Δ[Q(d)]<0时,表示比前一日器测容积含水率减少。订正后的容积含水率增值的计算方法依此类推。
2 结果与分析
2.1 发现A1出现负值和<0.1的小值不合理——以监利站、房县站为例
2.1.1 监利站降水和归一化频率实况 监利站2020年3—4月逐日降水量情况如下,3月10—24日无降水,3月25日雨量54.5 mm,4月12—17日无降水,4月18—20日的日雨量依次为22.6、7.5、26.7 mm。
监利站8个层次的2020年3—4月逐日20:00传感器归一化频率及日雨量折线如图1所示。利用图1中的SF,计算每一个对应的器测容积含水率。如3月24日60 cm归一化频率SF=0.836 7,代入式(3)得容积含水率器测值为33.410;再将A0=65.554,A1=-0.745 3,代入式(5)得到容积含水率终值40.61。
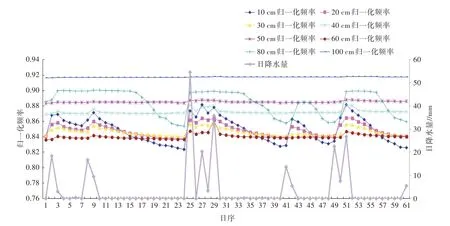
图1 监利站2020年3—4月逐日各层土壤归一化频率及日降水量日序变化
2.1.2 监利站2次强降水后归一化频率、容积含水率终值增值分析3月25日、4月18—20日是监利站2次强降水过程。监利站2次强降水后归一化频率增加百分比如表1所示,2次强降水后容积含水率终值的增加百分比如表2所示。
由表1和表2可见,2次强降水过程后,8个层次中除土壤测量深度60 cm外,土壤归一化频率、容积含水率终值的综合增加百分比均为正值。60 cm土壤综合增加百分比为1.14%,但容积含水率增加百分比为-1.82%,也就是说出现大的降水后,容积含水率下降,且降幅较大。对于以上归一化频率值对降水正响应、容积含水率终值对降水负响应的情况,从考察器测容积含水率对降水的响应情况来追根溯源。
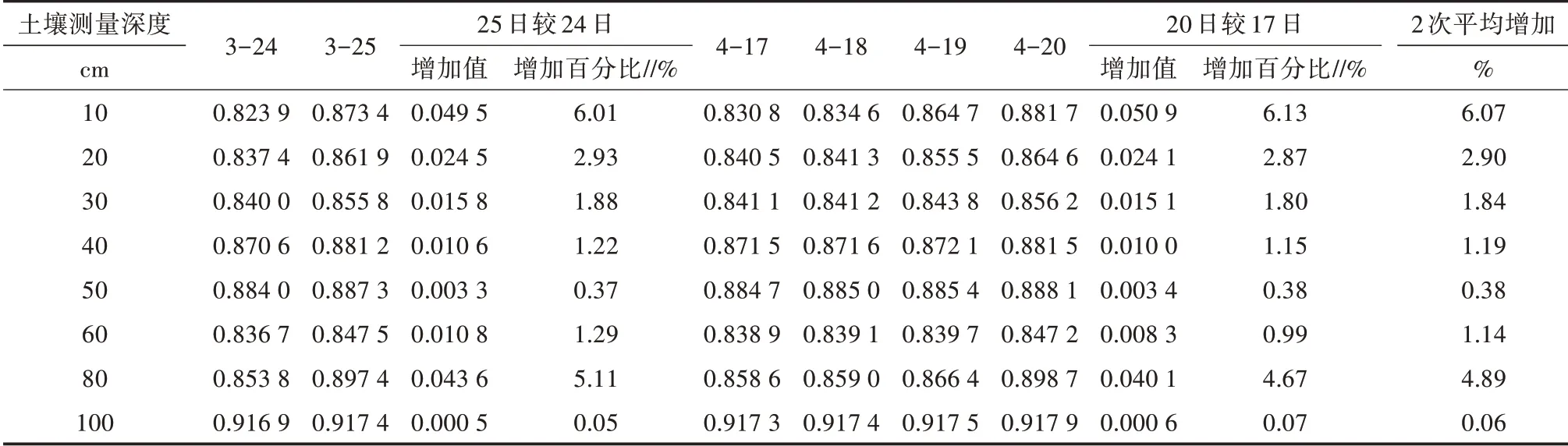
表1 监利站2次强降水后归一化频率增值情况
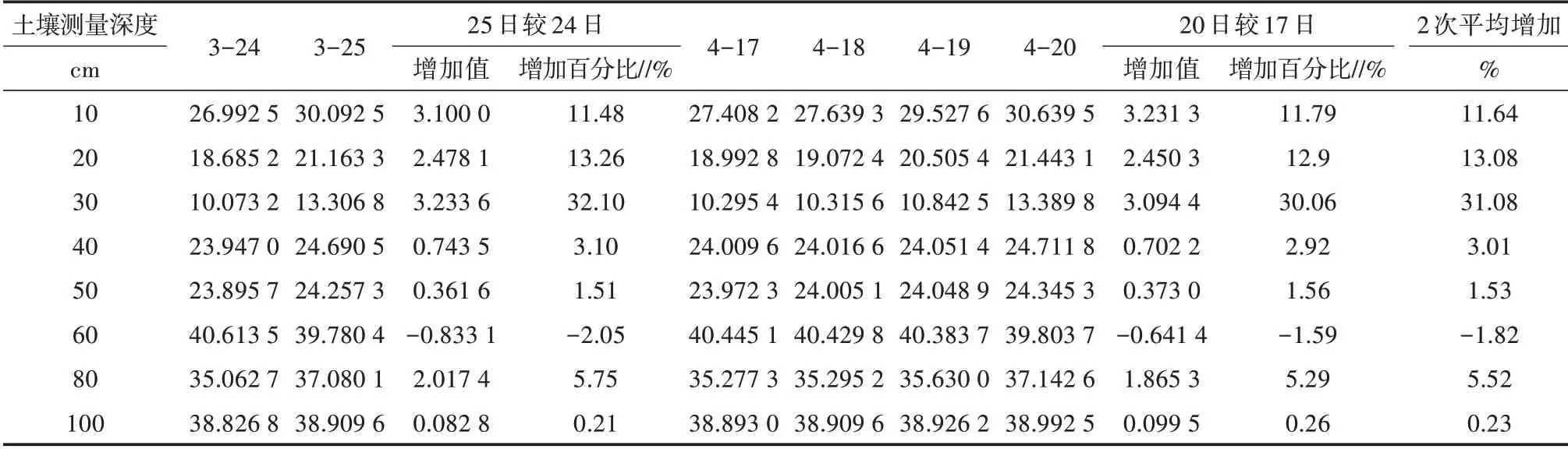
表2 监利站2次强降水后容积含水率终值增值情况
2.1.3 土壤容积含水率斜率项订正系数A1为负值的表现与讨论 监利站2020年3月土壤测量深度60 cm容积含水率逐日增值如表3所示。从表3可见,2—31日“器测容积含水率增值”和“订正后容积含水率增值”30对数据符号完全相反。如3月25日强降水后,器测容积含水率比前一天增加了1.118,订正后的容积含水率比前一天却减少了0.83。监利站土壤测量深度60 cm容积含水率标定方程截距A0和斜率A1分别为65.554、-0.745 3。相反地是,监利站土壤测量深度60 cm外的7个层次斜率系数A1均大于0。
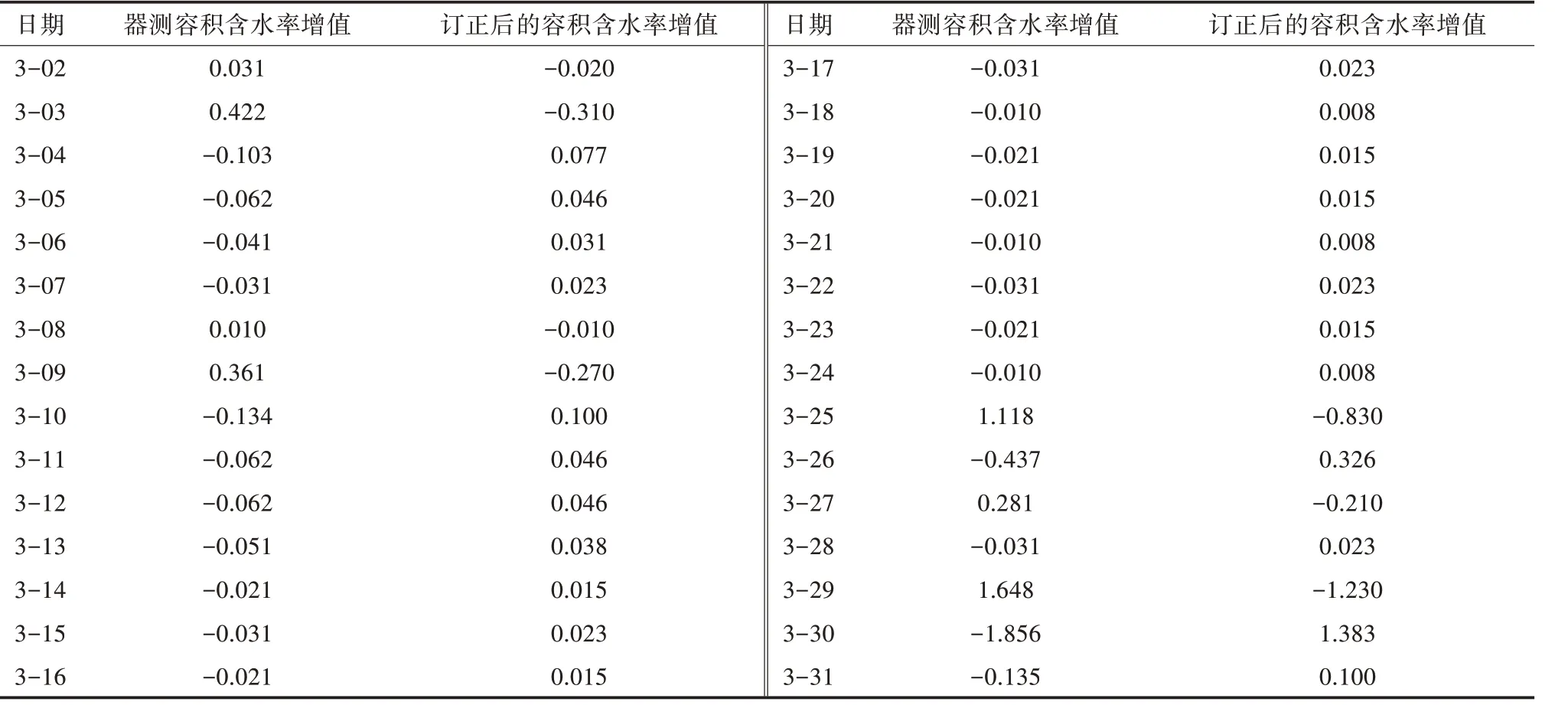
表3 监利站2020年3月60 cm容积含水率逐日增值 (单位:%)
在标定方程式(5)中,器测容积含水率、容积含水率终值随时间变化,均是时间的函数。在标定方程两边同时对时间t求偏导数:

因此,标定方程式(5)中,斜率A1实际上是将器测容积含水率随时间的增值放大的倍数。当A1<0时,容积含水率终值和器测容积含水率的随时间变化呈反位相,即当器测容积含水率随时间增加时,容积含水率终值却随时间减少,这样就违背了DZN系列土壤水分站测湿工作原理。
2.1.4 订正系数A1<0.1时的表现 房县站2020年7—10月10 cm标定方程式(5)的斜率项A1=0.005 7,截距项A0=25.604。房县站2020年7—10月土壤测量深度10 cm逐小时容积含水率终值与降水量的变化见图2。由图2可以看出,因斜率项太小,容积含水率终值大小基本受截距项左右,稳定在25%左右。故土壤容积含水率斜率项订正系数A1不能太小。
有鉴于清季官场用人乱象和运作机制的紊乱,北京临时政府认为在改建共和之际,用人行政不能新瓶装旧酒,理当有革故鼎新之气象。据《大公报》载,“目前袁总统特谕亲族及幕友人等,现改共和政体,革故鼎新,自应除百弊,凡有用人行政,原属公权,殊非一人之私,嗣后简任官缺均须选用贤才,汝等各宜自爱,不准徇情滥举,援引私人”⑧。袁世凯颁布命令,主张“以慎重用人为要素”,决计概不起用因赃私而去任的旧清大员,将劣迹照章,并对这些前清旧员另单存记,总计20多名,“以防日久有人推荐,混迹其间”。⑨
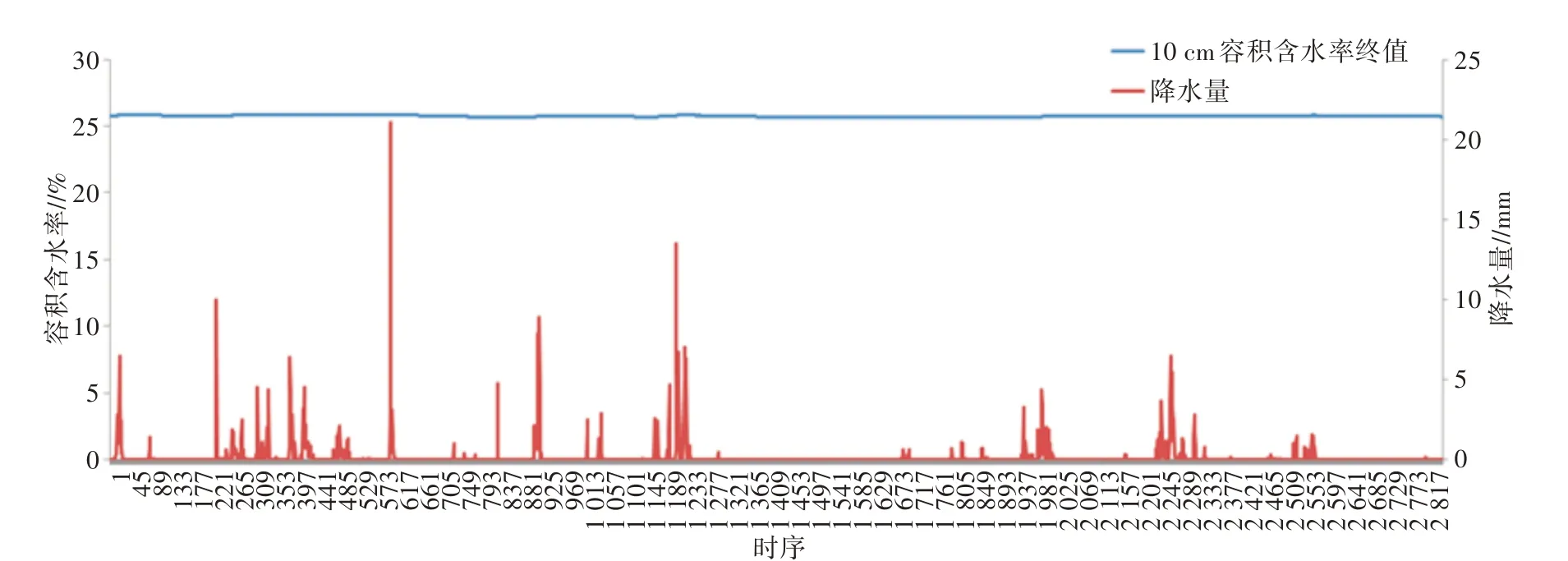
图2 房县站2020年7—10月土壤测量深度10 cm逐小时容积含水率终值与降水量时序变化
2.2 土壤容积含水率2个订正系数的界限值
2.2.1 订正系数的界限值初值的确定 在标定方程式(5)中,器测容积含水率X大于0。A1既不能为负值,也不能太小。根据相关研究,容积含水率的上限值为60%(土壤水分自动站逐小时资料质量控制方案(2016版)国家气象信息中心)。此外,根据式(3),绘制湖北省容积含水率(%)与归一化频率关系(图3)。归一化频率的上限值是100%(也就是1)。由图3可见,当容积含水率为53%时,归一化频率SF超过1。
由式(2)可知,归一化频率SF大于0.028 52,当SF=0.028 746 5时,器测容积含水率为2%(图3)。除非是在极度沙漠化地区,器测容积含水率的极小值应该不会小于2%,故设器测容积含水率的下限值为2%。
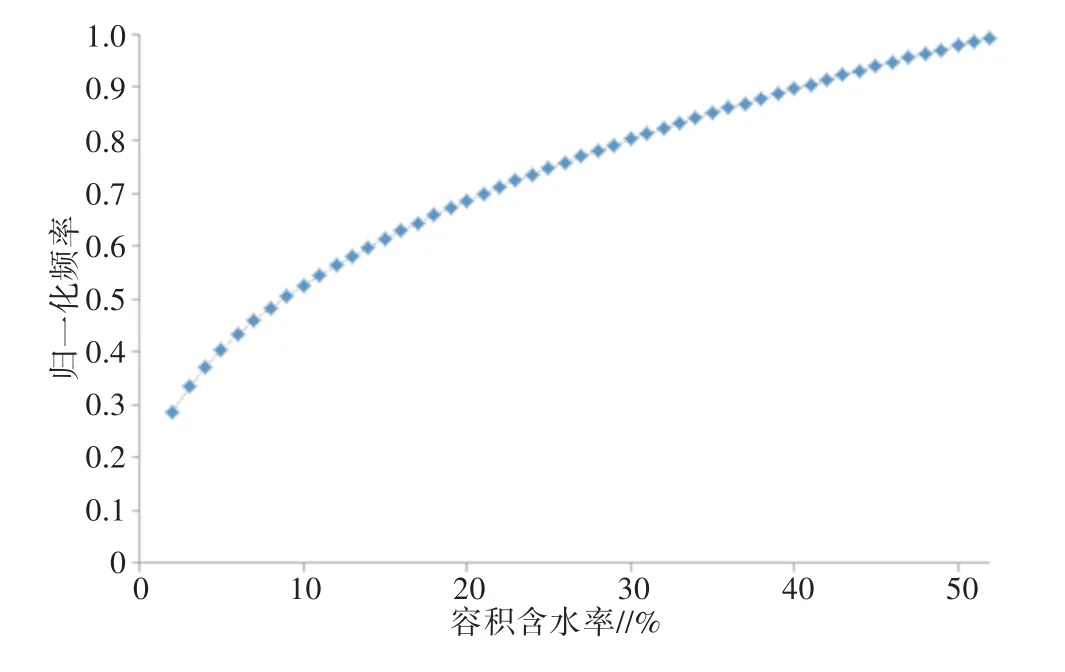
图3 湖北省归一化频率与容积含水率的关系
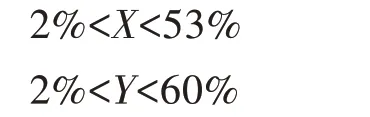
假设实际容积含水率随时间的增值为50%,相应的器测容积含水率随时间的增值仅为5%;或者实际的容积含水率随时间的增值仅为5%,相应的器测容积含水率随时间的增值却为50%,器测容积含水率随时间的增值与实际的容积含水率随时间的增值被放大(缩小)10倍,器测容积含水率就失去了它自身的意义。这种情况下,需要从仪器的性能、安装环境、现场标定角度找原因。
不妨将器测容积含水率随时间的增值与实际的容积含水率随时间的增值的放大(缩小)倍数达10倍作为A1界限值标准。
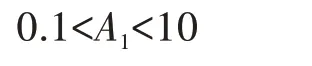
以X、Y、A1的界限值确定A0的界限值。
根据式(5)可得:
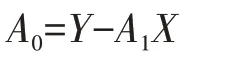
由表4可知,A0的范围太大,远超出了Y的界限值。在式(5)中,Y的组成主体应该是A1X,其次才是A0。放宽A0在Y中的占比到60%以下,则有

表4 土壤容积含水率2个订正系数的界限值试算
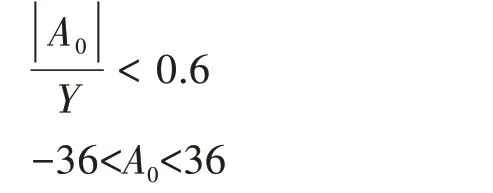
综上所述,A0、A1的界限值分别为-36<A0<36、0.1<A1<10。
2.2.2 湖北省订正系数界限值的经验值 根据湖北省46个自动土壤水分站(每站土壤测量深度分别为10、20、30、40、50、60、80、100 cm,共8个层次)A0和A1土壤容积含水率订正系数在实际中的表现,得出一般情况下湖北省土壤容积含水率订正系数阈值。
以10~30 cm为浅层,40~50 cm为中层,80~100 cm为深层,平原低洼地区60 cm为深层,鄂西北、山地丘陵地区60 cm为中层。湖北省土壤平均情况是上干下湿,且一般来说,浅层土壤湿度受降水、气温、光照的影响最大,变幅也最大;深层土壤湿度大,且变幅最小;中层土壤湿度变幅介于浅层、深层之间。
根据湖北省历年人工土壤水分观测资料,同时考虑强降雨积水后的过饱和状态(因人工取土时土钻不可能取出过饱和的水滴),得出湖北浅层土壤相对湿度年变幅在40%~80%;中层土壤相对湿度年变幅在20%~70%;深层土壤相对湿度年变幅在10%~60%。一般情况下,湖北省饱和状态下(非过饱和状态)容积含水率的值为36%~45%。
容积含水率变幅=饱和状态容积含水率×相对湿度变幅。
由相对湿度变幅、湖北省饱和容积含水率的范围值推导出容积含水率变幅,见表5。如浅层容积含水率变幅百分率的下限为14.4%;浅层容积含水率变幅的上限为36.0%。
计算湖北省2016年7月到2017年12月所有观测站(层)的器测容积含水率与容积含水率终值小时值的相关系数r1,如不出现特殊情况(比如更换仪器感应探头),理想状况下其相关系数应接近1。
利用2013年经过质量控制的中国气象局业务化自动土壤水分观测站实况数据、青藏高原试验观测数据及国际同类产品对CLDAS模拟结果进行评估[21],结果表明,从各省以及全国平均结果来看,相关系数普遍在0.8以上。
计算湖北省2016年7月到2017年12月所有观测站(层)的器测容积含水率与CLDAS容积含水率小时值的相关系数(r2)。r2越大,认为器测容积含水率值越能够正确地反映土壤水分的变化方向,仪器性能好、安装维护也到位。
计算湖北省2016年7月到2017年12月所有站(层)器测容积含水率的极差(最大值与最小值相减)、容积含水率终值的极差、CLDAS容积含水率的极差。
挑取r1>0.8、r2>0.6且容积含水终值的极差位于表5中对应层次“容积含水率变幅加宽”上、下限内的站(层)的资料,统计湖北省A0、A1界限值实况。由表5可见,湖北省A1的取值范围为(0.294 9,1.531 1);A0的取值范围为(-19.823,34.785)。将上述范围略作扩大,一般情况下,湖北省土壤容积含水率2个订正系数的界限值为0.25<A1<1.57、-20<A0<35。以下是2个相关实例。
在表6中,“sf_dif”表示归一化频率的极差;“sw_dif”表示容积含水率器测值的极差;“obs_dif”表示容积含水率终值的极差;“cldas_dif”表示CLDAS容积含水率的极差。

表6 麻城、竹溪站各层土壤水分极差情况
麻城站土壤测量深度100 cm容积含水率器测值极差“sw_dif”大于土壤测量深度50、60、80 cm,违背了浅层土壤湿度变幅大于深层的常理,土壤测量深度100 cm对应A1的值为0.294 9,将其器测容积含水率的变幅压缩至原来的约1/3。麻城站土壤测量深度100 cm是订正效果较好的例子,如图4所示。
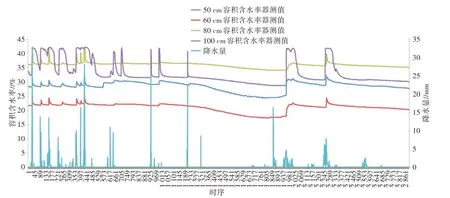
图4 麻城站2020年7—10月逐小时容积含水率器测值与降水量时序变化
由图5可以看出,在排除套管进水的前提下,竹溪站土壤测量深度60、80、100 cm器测容积含水率3条线起伏大体一致。仔细观察,各时间点土壤测量深度60、80、100 cm器测容积含水率依次由小到大;每次降水后的土壤测量深度60、80、100 cm器测容积含水率上升时间点依序后推,并且上升幅度依次由大到小;每次降水停止后土壤测量深度60、80、100 cm器测容积含水率下降时间点依序后推,并且下降幅度依次由大到小,真实反映了土壤水分的变化。土壤测量深度100 cm对应A1=0.154 8,订正后的容积含水率变幅不到器测容积含水率变幅的1/6,订正效果适得其反。因竹溪站土壤测量深度100 cm不符合r1>0.8、r2>0.6的标准,未被纳入表5中A0、A1界限值实况统计。
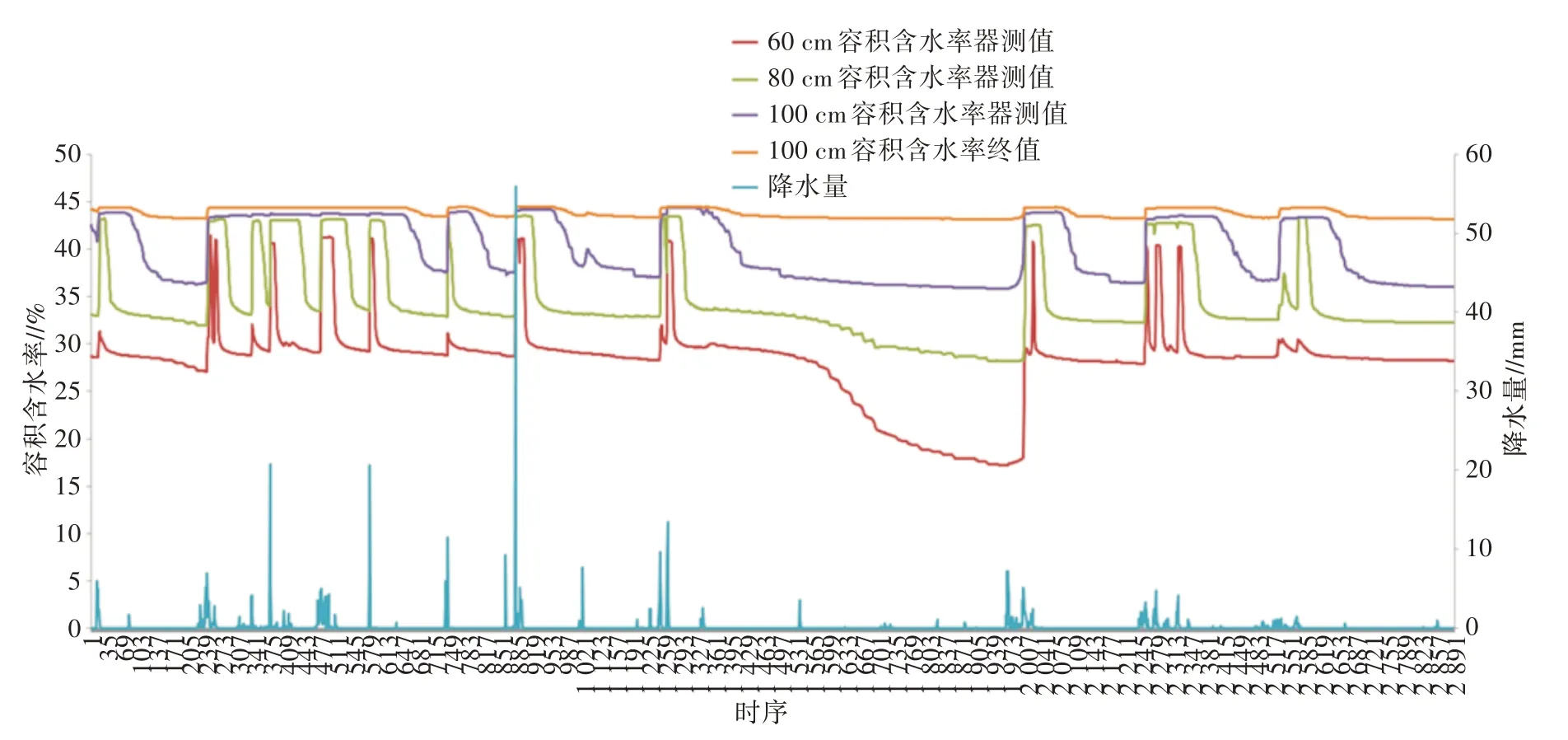
图5 竹溪站2020年1—4月逐小时土壤测量深度60~100 cm容积含水率器测值、土壤测量深度100 cm终值及降水量时序变化
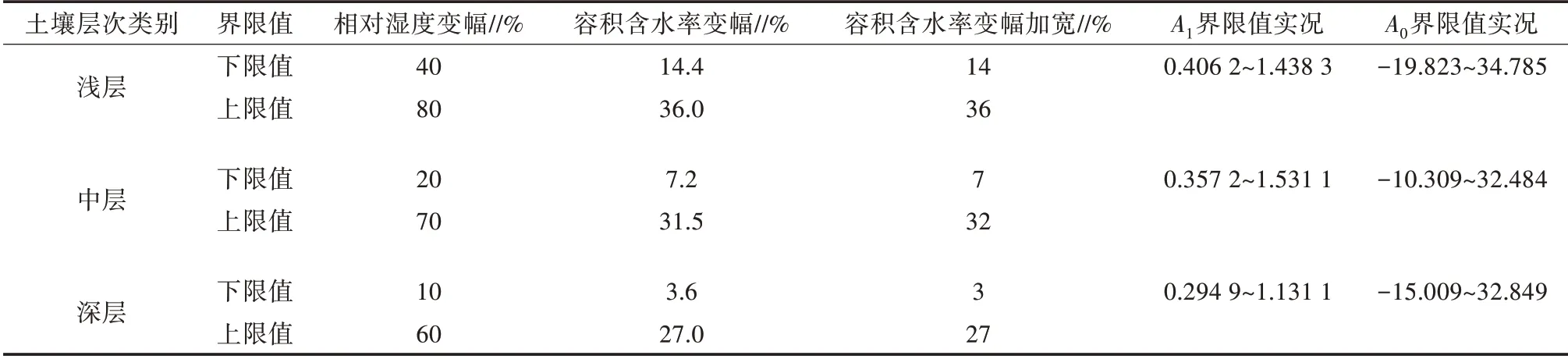
表5 湖北省土壤各层次容积含水率年极差(变幅)对应A0、A1界限值
3 小结
DZN3型土壤水分自动站测湿中,将土壤容积含水率器测值转换为终值的标定方程为Y=A0+A1X。在实际工作中,各种因素均可能会造成容积含水率订正系数A0和A1的不准确或者错误,这2个系数的阈值范围是进行土壤水分数据质量控制的重要参考。
1)A1<0违背了DZN系列土壤水分站测湿工作原理,且A1不能太小。本研究通过对湖北省监利站2020年3—4月2次强降水过程出现前后自动站测湿资料的计算发现,当A1<0时,容积含水率终值和器测容积含水率随时间的变化呈反位相。也就是说当器测容积含水率随时间增加时,容积含水率终值会随时间减少,这样就违背了DZN系列土壤水分站测湿工作原理。从房县站2020年7—10月10 cm逐小时容积含水率终值与降水量的变化分析,如果斜率项A1太小,容积含水率终值会稳定在A0附近。故土壤容积含水率斜率项订正系数A1不能太小。
2)湖北省2个系数的阈值范围为A0(-20<A0<35)和A1(0.25<A1<1.57)。通过对Sentek公司DZN3型自动土壤水分观测仪出厂时提供标定频率和容积含水率之间的关系公式进一步推导分析,得出了2个系数的阈值范围分别为A0(-36,36)和A1(0.1,10)。结合湖北省实际情况,得出湖北省2个系数的阈值范围为A0(-20,35)和A1(0.25,1.57)。文中对2个系数阈值范围逐步设定过程,可能对仪器的性能要求较高,加之湖北省已有的系数样本个例有限,相关问题还有待进一步探讨。
3)提高标定系数质量的建议。①作好田间标定对比观测,建议进行邻站对比、单站双套站对比;②加强对特殊状况,如土壤空虚层、仪器套管安装贴合状态不良、套管内部空间的干燥剂失效、底部积水、部分触点锈蚀等相关数据特性的分析;③出台类似《地面气象观测规范》中地温场维护整理规定的土湿场整理规定(包括表层松土、植被状况等)。田间标定方法中,人工与自动土壤水分对比观测资料是计算订正系数A0和A1的基础。人工每次观测的是土壤重量含水率,它需要乘以土壤容重才能得到容积含水率,故除了要保障每次土壤重量含水率的数据正确,作为常数的土壤容重大小更应该真实可靠。

