基于陷波滤波器的伺服系统机械谐振抑制
杨 光,丁玉发
(沈阳师范大学 数学与系统科学学院,沈阳 110034)
0 引 言
在现代化工业进程中,伺服系统作为核心部件被广泛应用。伺服系统主要由速度环、电流环以及二质量系统构成,二质量系统又由电机、负载以及它们之间的传动装置连接而成。然而,这些传动装置并不都是理想刚性结构,大多采用机械负载与旋转电机驱动之间的弹性耦合机械结构。弹性耦合机械结构包含固有的谐振频率,在执行高动态动作指令时可能会产生明显的机械振动[1],长时间的振动会导致传动部件转矩过大而受损,降低设备的使用寿命,甚至会直接使设备报废,因此有效抑制机械谐振是十分重要的。
针对谐振抑制问题,有许多解决办法。这些解决方法主要有主动和被动2种方式。主动方式主要通过改变设计的控制器的参数或结构抑制机械谐振;被动方式则是在保持系统的其他设计不变的前提下,通过在伺服系统中级联陷波滤波器达到抑制谐振的目的。主动方式主要分为基于PI的反馈控制[2-3]、PI控制[4-5]以及其他许多高级算法[6-8]等。利用极点配置设计PI控制器,虽然可以利用改变闭环系统的阻尼系数改善伺服系统的性能[9],但这种方法也存在一定的缺陷。利用模型预测控制器也可以抑制机械谐振,这一方法可以通过对电磁转矩进行预测输出达到目的,但是该方法也有一定的局限性,这种方法在轴系刚度等电机参数已知的条件下才能使用,而实际上这些参数是未知的,而且又不易辨识,因此在工业领域的应用价值并不高[10]。
本文提出了一种在伺服系统中级联陷波滤波器的方法进行谐振抑制。通过在系统中加入陷波滤波器,根据已知的谐振频率,并考虑相角裕度和幅值与阈值的相对大小,直接确定陷波滤波器的参数,并不需要手动调节参数,从而使之既能抑制谐振又能保持系统稳定,还可以提高抑制的效率。
1 模型建立
图1是简化的二质量系统的模型。

图1 二质量系统模型Fig.1 Two mass system model
为了便于分析,设传动部分无间隙,忽略电机的摩擦转矩,可以得到如下的动力学方程:

(1)
其中:Jm和Jl分别表示等效电机惯量和等效负载惯量;ωm和ωl分别表示电机侧和负载侧旋转的角速度;θm和θl分别表示电机侧和负载侧旋转的角度位置;Te表示电机的输出转矩;Ts表示弹性阻尼矩;Tl表示电机的负载转矩;Ks表示传动刚度;KW表示粘滞阻尼系数。
二质量系统传动部分的传递函数为
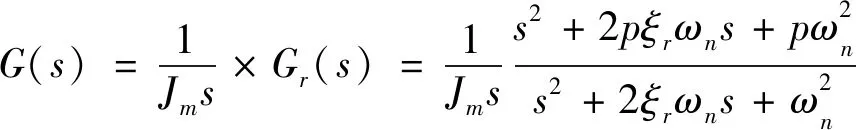
(2)
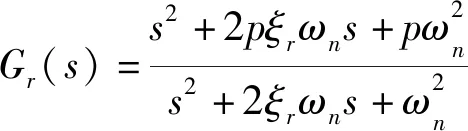

图2 谐振环节的Bode图Fig.2 Bode diagram of resonance link
其中谐振和反谐振频率分别为Bode图中幅值最大点和最小点对应的频率。
通常,二质量系统的电机与负载之间存在弹性传动,这就使得传动部分的传递函数产生2个复共轭极点,因而导致伺服系统机械谐振的发生。根据控制系统的稳定性条件[11],本文主要采用在伺服系统中级联陷波滤波器进行谐振抑制。其中,陷波滤波器的作用就是消除这一对共轭极点,或者将其调整到优化位置[12],从而谐振抑制。本文在传统的陷波滤波器参数确定方法上进行改进,结合考虑相角裕度和幅值与阈值的相对大小,直接确定出陷波滤波器的宽度和深度参数,从而提高谐振抑制的效率。
2 陷波滤波器设计
陷波滤波器作为一种常用的带阻滤波器,主要通过将某一频率点的输入信号迅速衰减到指定范围,从而阻碍该频率信号的通过。陷波滤波器的优点在于可以将指定频率点处的幅值衰减到特定值以下,对其他频率点没有任何影响,目前广泛采用的是谐振抑制方法。
2.1 陷波滤波器的原理
典型的陷波滤波器的传递函数为

(3)
其中:ω0是陷波中心频率;ξ是深度参数;k是宽度参数。
将陷波滤波器与二质量系统级联[13-14],并根据确定出的谐振频率调节陷波滤波器的参数抑制谐振。于是根据上述分析,级联陷波器的传递函数为
G0(s)=Gr(s)GN(s)
(4)
2.2 陷波滤波器的参数确定
由式(2)可知,当电机的参数已知时,伺服系统的谐振频率便确定下来。利用陷波滤波器进行谐振抑制需要确定如下参数:陷波的中心频率ω0、陷波的宽度k以及深度ξ,其中中心频率ω0就是谐振频率ωn。因此,本节将重点分析陷波滤波器的宽度参数k和深度参数ξ对谐振的影响,以及这2个参数的确定方法[15]。
2.2.1 深度和宽度参数分析
对式(3)选用不同的深度和宽度参数,由文献[16]可知,当宽度参数固定时,逐渐增大深度参数,陷波中心频率处的幅值衰减也逐渐增大,而对应的相角裕度逐渐减小;当深度参数固定时,逐渐增大宽度参数,陷波中心频率处的幅值衰减也逐渐增大,而对应的相角裕度逐渐减小。因此,如果深度和宽度参数选取过大,会使相角裕度变小导致系统不稳定,所以利用陷波滤波器进行谐振抑制时应选择适当的宽度和深度参数,保证在抑制谐振的同时还能维持系统的稳定性。
2.2.2 宽度参数和深度参数的确定方法
设定一个阈值Hth,当中心频率ω0处的幅值在阈值以下时认为不发生谐振。如图3所示,二质量系统的幅频特性曲线与阈值有2个交点,交点横坐标记为ω1和ω2。利用陷波滤波器对二质量系统进行谐振抑制,将其所有频率点处的幅值衰减到阈值以下,即使得级联陷波器在ω1,ω2以及中心频率ω0处的幅值全都低于阈值Hth。

图3 给定参考阈值下二质量系统的Bode图Fig.3 Bode diagram of two mass system with given reference threshold
由式(4),级联陷波器的传递函数为
令s=jω,则可以确定级联陷波器在任一频率点处的幅值:

(5)
由式(5)可以计算出级联陷波器在ω1,ω2和中心频率ω0处的幅值H(ω1),H(ω2),Hmax,于是得到一个不等式组:

(6)
解不等式组(6),可以得到关于陷波的宽度k和深度ξ的不等式。
要想既能抑制谐振,又能保持系统的稳定性,需保证相角裕度γ≥45°,其中相角裕度γ=180°+argG(jωc),ωc称为剪切频率。于是得到
γ=180°+argG(jωc)≥45°
(7)
解不等式(7),又可以得到关于陷波的宽度k和陷波的深度ξ的不等式。联立式(6)和式(7),即可以得到陷波的宽度k和深度ξ的值。
3 仿真与讨论
根据第2节中提出的陷波滤波器的参数确定方法,现对实验结果进行仿真。

表1 伺服系统机械仿真的参数Table 1 Parameters of servo system mechanical simulation
根据式(2)可以算出,谐振频率ωn=281.276 2,谐振阻尼系数ξr=0.110 5,谐振反谐振比系数p=0.177 0。由上述提出的参数确定方法,得到陷波滤波器的中心频率ω0=281.276 2,陷波深度ξ=0.375 5,陷波宽度k=37.081 4。抑制前后的Bode图如图4所示。
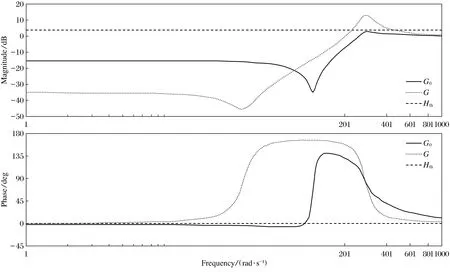
图4 抑制前后二质量系统的Bode图Fig.4 Bode diagram of two mass systems before and after suppression
从图4可以看出,二质量系统在ω1,ω2以及中心频率ω0处的幅值均降到阈值以下,此时认为系统不发生谐振,这就说明了机械谐振得到了有效抑制。
4 结 论
在工业领域中,伺服系统作为核心部件应用广泛。在伺服系统中,机械谐振是降低机器寿命的主要原因,长时间发生机械谐振就会降低机器的寿命甚至会使设备报废,因此抑制机械谐振是十分重要的。本文提出了在伺服系统中加入陷波滤波器的方法,在保证系统在等于阈值的频率点处以及谐振频率处的幅值都低于阈值的前提下,通过增大相角裕度保持系统的稳定性,直接确定出陷波器的参数,克服了以往手动调节陷波滤波器参数的缺陷,从而既能抑制谐振,又能使系统稳定,还能提高谐振抑制的效率。由此带来的经济及社会效益也将会是非常可观的。

