基于固结试验的Duncan-Chang参数反分析方法

王江营，雷 文，蒋中明,5，余元君，纪炜之，林 飞，张拥军，王导勇

（1. 长沙理工大学水利工程学院，湖南 长沙 410114； 2. 湖南建工集团有限公司，湖南 长沙 410004；3. 湖南省洞庭湖水利事务中心，湖南 长沙 410007； 4. 湖南省水利水电勘测设计研究总院，湖南 长沙 410007； 5. 水沙科学与水灾害防治 湖南省重点实验室，湖南 长沙 410114）

土体变形计算是土力学三大主要问题[1]之一，国内外学者为此提出了种类繁多的本构模型和计算方法。大量的工程实践表明，Duncan-Chang 模型具有很好的适用性和精确度[2～6]，特别是随着各类数值计算软件飞速发展，在土体变形计算中通常都需要用到Duncan-Chang 参数[5～7]。

众所周知，Duncan-Chang 模型[2]共包含8 个参数，分别是C、φ、Rf、K、n、G、F 和D，需要通过三轴固结排水试验进行测定，而对于许多中、小型工程来讲，因为受制于经费预算和工期，往往不会开展这方面工作，进而会对后续计算分析造成影响。因此，一些专家在不断研究在缺少试验资料的情况下，如何近似推求土体的Duncan-Chang 参数。王志亮和殷宗泽等[3]基于土体K0状态条件，针对缺少三轴试验结果的情况，提出了可适用于砂土和黏性土的切线泊松比计算公式；曹文贵等[4]基于土体变形的非线性特征，充分考虑初始应力和附加应力对土体变形模量的影响，建立出了无需使用土体压缩试验曲线或静载试验曲线的Duncan-Chang 模型沉降计算方法；彭长学等[8]针对软土压缩曲线接近双曲线方程的特点，提出以土体初始孔隙比和压缩模量确定其e-p 曲线方程，进而可确定Duncan-Chang 模型的切线模量，但是这种方法无法考虑土体侧向变形的影响；在此基础上，杨光华等[9]利用e-p 曲线推求了软土的非线性切线模量；孙明正等[10]结合具体工程，对已有的Duncan-Chang 模型参数推求方法进行了验证和敏感性分析，计算结果显示虽然存在一定偏差，但考虑到岩土工程的复杂性，仍具有较大的借鉴意义。

综上所述可知，现有方法多是利用土体的e-p 曲线来推求其切线模量，并与Duncan-Chang 模型相结合，以用于沉降变形计算，但是其所能获得的Duncan-Chang 参数比较有限，有关计算精度亦难以保证，且较为繁琐。为此，本文拟通过对土体标准固结试验进行数值模拟，并与其试验所得的e-p 曲线相结合，以期建立出一种更加便捷可行的Duncan-Chang 参数反演分析方法。

1 Duncan-Chang 参数反演思路

Duncan-Chang 模型包含了8 个参数，其中粘聚力C 和内摩擦角φ 可通过直剪试验求得，直剪中的慢剪与三轴固结排水试验具有较好的共通性；土体的破坏比Rf一般在0.60～0.90 之间，当缺乏试验数据时，可根据土体的种类近似取值，如黏性土的破坏比通常可取0.80，砂性土可取0.65[3]。

同时，在数值计算中K、n、G 和F 为常用参数，土体的切线弹性模量与切线泊松比与它们相关性较强，通常不会用到参数D[8-10]。因此，只需对K、n、G 和F 等参数进行反演，具体思路如下：

1）建立标准固结试验数值计算模型，确定计算边界条件、计算荷载及加载过程。

2） 拟定标准固结试验数值模型初始Duncan-Chang 计算参数。

3）进行标准固结试验的数值计算，获得数值计算下土体e-p 曲线。

4） 重复变化标准固结数值试验的Duncan-Chang 参数，再次进行数值计算，获取新的数值计算ep 曲线。

5） 采用最小二乘法优化算法，建立Duncan-Chang 参数与e-p 曲线的非线性函数关系。

6）将标准固结物理实验的e-p 曲线成果作为输入条件，反求Duncan-Chang 参数。

7）将反求得到的Duncan-Chang 参数再次用于标准固结实验的数值计算，获得新的e-p 曲线。

8）对反演参数获得的e-p 曲线进行误差分析，当误差满足要求时，“6）”所求得的Duncan-Chang 参数即为最终结果。

2 标准固结试验数值模拟计算

2.1 计算模型

根据土工试验标准中标准固结试验试样制作标准，利用有限元软件Ansys 建立一个直径为6.18 cm，高为2.0 cm 的圆柱体压缩试样模型，并进行网格划分，如图1 所示，再将其导入有限差分软件FLAC3D中，模拟标准固结试验，试验本构模型采用邓肯-张非线性弹性模型+摩尔-库伦模型。

图1 标准固结试验数值计算模型

2.2 标准固结试验数值计算过程

首先，对圆柱体压缩模型赋材料参数，其中C、φ值可由直剪试验得到，约束圆柱试样底面边界和周围边界，对模型设定重力加速度，计算出试样在自重作用下的位移并清除。

然后，根据标准固结试验加载顺序和步骤，按照压力等级为50 kPa、100 kPa、300 kPa、400 kPa 对试样进行逐级加载计算。

最后，利用Fish 语句编辑孔隙比、压缩系数和压缩模量计算式，输出结果（e-p 曲线）。

由于FLAC3D只能通过Fish 程序获取单元的体积应变增量和当前体积，无法直接获取当前的孔隙比，因此，可通过一些推导来获取单元体当前的孔隙比。

假定土体总体积为V，孔隙体积为Vv，固体颗粒体积为Vs，初始孔隙比为e0，荷载作用下体积变化量为ΔV，则土体体积应变εv为：

此时土体孔隙比e′为：

进而可得：

式中 e′——试样体积变化后的孔隙比。

因此，在Fish 程序中，只需获得每一级加载后试样的体积应变增量，即可计算得到此时的孔隙比。针对4 组不同压力，计算得到试样固结稳定后的孔隙比，以孔隙比为纵坐标，压力为横坐标，即可得到相应的e-p曲线。

2.3 建立非线性函数关系

为了建立Duncan-Chang 参数与e-p 曲线的非线性函数关系，需拟定不同的初始参数，通过数值计算得到相应的e-p 曲线，然后采用非线性最小二乘法优化算法，建立它们之间的函数关系。

非线性最小二乘法是通过最小二乘分析，用m 个观察点来拟合有n 个参数的非线性模型（m＞n），即考虑m 个数据点的集合，（x1，y1），（x2，y2），...，（xm，ym），以及一个曲线（模型函数）y=f（x，β），它除了变量x 外，还依赖于n 个参数β=（β1，β2，...，βn）。希望能找到参数矢量β，从而使得曲线在最小平方的意义上最好地拟合所给定的数据，也就是平方和最小，从而可建立出不同压力p 下，土体孔隙比e 与Duncan-Chang 参数的关系式。

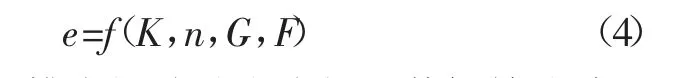
以湖南省沱江排水闸地基土为例，其初始孔隙比e0=0.67，通过拟定50 组初始参数，可以得到相应的ep 曲线，如表1 所示为不同参数和压力下土体最终的孔隙比。

表1 土体孔隙比试算结果

进而，可拟合出压力p 分别为50，100，300，400 kPa 时，土体孔隙比e 与K，n，G，F 等参数之间的函数关系式：

3 试验验证

将该土体标准固结物理实验的e-p 曲线作为输入参数，利用式（5）可求得到相关Duncan-Chang 参数：K=70.01，n=0.65，G=0.37，F=0.050。

进而，再将上述反求得到的Duncan-Chang 参数作为初始值，用于标准固结实验数值模拟，又可得到不同压力p 对应的孔隙比e，如表2 所示。

表2 不同方法下土体的孔隙比

同样可求得此时的e-p 曲线，可将其与试验结果绘制在一起，如图2 所示。

图2 不同方法下土体的e-p 曲线

由表2 可知，数值计算每级荷载作用下土体孔隙比e 与物理试验实测值误差较小，最大不超过3%；图2 中数值模拟和物理试验得到的e-p 曲线同样偏差较小，其精度可满足要求。此时，可认为由式（5）反求得到的Duncan-Chang 参数即为最终结果，表3 所示为反演计算结果和三轴固结排水试验的实测结果。

表3 土体Duncan-Chang 参数反演值与实测值

由表3 可知，本文方法所得结果相对文献[3]方法的结果更为理想。其中，K、n、G 等3 个参数的相对误差较小，最大不超过5%，而F 值相对误差较大，这是由于F基数很小，对数值模拟结果比较敏感，但误差范围仍在10%以内，对于数值计算来讲是相对可以接受的，即表明了本文所提出的Duncan-Chang 参数反演分析法是合理可行的。

4 结 论

1）利用有限差分软件FLAC3D，利用Fish 语句编辑土体孔隙比、压缩系数和压缩模量的计算公式，建立了土体标准固结试验数值计算方法。

2）基于土体标准固结试验数值计算结果和最小二乘法优化算法，建立出了Duncan-Chang 参数反分析方法。

3）本文建立的Duncan-Chang 参数反分析方法合理可行，能够满足相关数值计算要求。