基于VFIFE法的剪式铰结构建模研究①
杨玉龙,刘宇飞,李 萌,季京宣
(1.浙江大学 杭州 310058;2.中国空间技术研究院 钱学森空间技术实验室,北京 100094)
0 引言
剪式铰结构是一种应用广泛的展开结构,由多个剪式铰单元组成。剪式铰结构最早由学者Pinero提出[1],目前得到广泛的研究和应用[2-9]。杆系结构展开过程的运动学和动力学计算分析,通常采用多体动力学[10-12]。可展杆系结构建模时,对于杆件模型,可以分为刚性杆和柔性杆。通常刚性杆比较简单,柔性杆相对复杂。
向量式有限元法(VFIFE,Vector form intrinsic finite element)是一种新型的数值算法[13-14]。其建模方法是将结构划分为节点,节点间通过单元连接。结合有限元理论,建立单元模型。利用牛顿第二运动定律,建立整个结构的节点方程组。该方程组不包含刚度矩阵,所以在解决大变形及非连续问题有一定优势。在静力学领域,向量式有限元法已取得了一定的研究结果。在动力学方面,Yang拓展了建模方法[15],提出了间隙铰的建模方法,同时进行了间隙结构的特性研究。Wu进行了连杆滑块结构的运动分析[16]。
用VFIFE来研究分析可展杆系结构,首先需要解决的就是建模问题,本文重点论述了杆件的建模方法,并对两种建模方法的计算结果进行比较讨论。
1 VFIFE基本计算过程
可展杆系结构的VFIFE算法,是将结构分解成节点和单元,利用牛顿第二定律,建立中值差分公式,进行迭代计算tn时刻各个节点的位置。利用单元计算各节点在运动过程中的内力,结合体系所受外力,计算各节点tn+1时刻的位置。重复迭代计算,直至运动结束,文献[15]对基本计算过程,进行了较为详细的描述。

图1 杆件单元划分

图2 时间历程划分
各节点位置计算公式为:
(1)
各节点速度计算公式为:
(2)
其中,F为结构节点所受外力,f结构节点所受内力,m为节点质量。
对于不同结构及其不同单元,节点所受内力是计算的关键。
2 剪式铰柔性杆模型节点内力计算
剪式铰柔性杆建模,主要方法是将一根结构杆件,划分为多个梁单元。梁单元两端的节点上,承受力和弯矩,存在平动位移和转角。针对一个剪式铰单元,为说明和显示方便,在销轴附近,各自划分单元c、d和k、l。销轴(Joint,用J表示)和销孔(Bearing,用B表示)的受力主要是:外力F,内力fp,以及各自单元的节点力fe(如图3):

图3 剪式铰受力分析
销轴和销孔的运动方程为:
(3)
因为:
(4)
故:
mJ(fekb+felb)-mBF]
(5)
3 剪式铰刚性杆模型节点内力计算
刚性杆是一种力学意义上的杆,是理想化的一种杆件,在运动过程,杆件轴线始终保持直线。针对刚性杆建模,提出强制几何约束,即一根结构杆件,仅考虑单元头尾两个节点位置,两个节点间所有几何点的坐标,按直线插值考虑。对于杆件中间出现的销轴和销孔位置,通过直线插值进行计算。与柔性杆的差异在于,不考虑杆件横向变形,并且仅考虑杆件轴力。
对于图3所示的剪式铰,假设运动过程中,杆件销轴和销孔的轴线出现偏差,这些位移差,会在销轴和销孔的节点上产生力,通过二者受力协调,从而保证两根杆件运动的协调。

图4 理想节点位移差图
对于一个剪式铰单元,假设剪式铰的销轴上存在力P,分别作用在杆1和杆2上,二者方向相反,大小相等,如图5所示,分别垂直于杆方向的分力为F1和F2,

图5 剪式铰受力分析
(6)
按拟静力学法,假设各杆为简支梁,在垂直于梁轴线方向力的作用下,会产生挠度Δf1和Δf2,则有:
(7)
(8)
式中,a和c为作用力距计算节点距离,l为杆长,E为材料弹性模量,I为截面惯性矩。
剪式铰轴处两根杆位移为e,则有:
e=Δ1+Δ2
(9)
根据以上各式,推导可得:
(10)
(11)
(12)
如果杆1与杆2几何参数完全一样,并且铰在杆中间时,则有:
(13)
对于剪式铰中的每一个杆件,杆两端节点力,可以根据F1和F2和几何关系获得。
4 计算与讨论
4.1 计算模型
对于一剪式铰杆系模型,结构基本情况如图6,图中单位为m。节点O固定,在节点A和B施加水平力50 N。展开过程中忽略摩擦力和重力,如果相邻节点间水平距离小于0.1 m,计算停止。

图6 剪式铰模型
4.2 结果讨论
根据以上提出的建模方法,编制程序进行计算。柔性杆模型和刚性杆模型展开过程图见图7和图8。从图中可以看出,柔性杆模型中,在销轴位置存在节点,刚性杆模型中,在销轴位置没有节点。从展开过程可以看出,柔性杆和刚性杆模型均能顺利展开,并且展开过程正常。
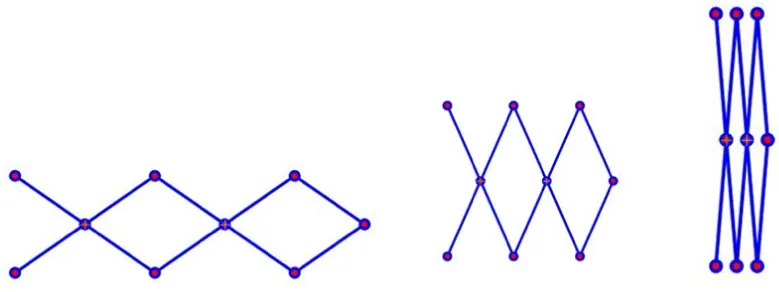
图7 柔性杆模型模拟展开过程

图8 刚性杆模型模拟展开过程
从图9结果可以看出,当满足展开条件时,柔性杆模型节点A位置为0.53253 m,刚性杆模型节点A位置为0.52613 m处,节点A横向坐标差为0.0064 m,为二者模型坐标位置均值的1.21%。两个模型均未达到理想位置,误差一方面来自于迭代步长,一方面来自于迭代误差。

图9 节点A展开过程横向坐标位置对比
从图10结果可以看出,当满足展开条件时,节点A横向速度差为0.0085 m/s,为二者速度均值的2.21%。图中可以看出,柔性杆模型节点A的横向速度略小于刚性杆模型的速度。但柔性杆模型展开时间却小于刚性杆模型,主要原因是柔性杆模型中,节点A所在杆件,直接受力,杆件有一定的横向弯曲,使得节点间的水平距离较早达到控制值0.1 m,计算停止,说明刚柔模型,对结构展开过程中位置精度有影响。

图10 节点A展开过程横向速度对比
柔性杆和刚性杆模型,计算结果存在差异,一部分原因是杆件刚柔存在差异,另外一部分原因来自于计算方法误差,这一部分需要后续研究中予以重视。二者的合理性,主要取决于模型分析的需要,考虑结构是以刚体运动为主,还是考虑杆件变形后的结构整体构型为主。
5 结论
基于向量式有限元法,本文提出了剪式铰刚性杆模型及其内力计算方法,同时推导了剪式铰柔性杆模型及其内力计算方法。两种方法均能顺利模拟展开过程。两种模型的模拟计算结果在展开位置精度、展开时间和展开速度存在微小误差。基于VFIFE法的展开过程的计算精度,在后续研究中需要重点关注。

