基于张量分解的知识超图链接预测模型

王培妍 段 磊 郭正山 蒋为鹏 张译丹

(四川大学计算机学院 成都 610065)

知识超图是一种图结构的知识库，通常以多元组的形式存储世界上的事实，其可以被视作知识图谱的推广.由于现实世界中存在大量事实，在知识库中获取并储存所有事实是不现实的.所以对现有知识库的最大挑战是其严重的不完整性，即部分实体间的链接是缺失的.以Freebase[1]为例，其储存有约300万的人物条目，其中71%的人缺少与出生地的链接，94%的人缺少与父母的链接，99%的人缺少与种族的链接[2].面对知识库的高度不完整性，手动为实体间添加链接是十分耗费人力和物力的，因此产生了对自动推理实体间缺失链接算法的需求.

链接预测算法能够基于实体间已知的链接去预测未知的链接，因此可以用于知识库补全，同时进一步促进基于知识库的下游任务，例如智能问答[3-4]、个性化推荐[5-6]、自然语言处理[7]和信息检索[8]等.自从谷歌在2012年发布了知识图谱(一种基于二元关系构建的图结构知识库)，基于知识图谱的链接预测开始受到关注，在社交网络分析[9]、生物医学[10]等领域中都取得了极大的进展.然而在现实世界中，关系通常是非二元的.例如“梁思成是李蕙仙和梁启超的儿子”，显然在这个事实对应的关系中共涉及到3个实体，分别为“梁思成”“李蕙仙”和“梁启超”，因此该关系是一种更为复杂的多元关系.有数据表明，在原始Freebase数据集中，超过1/3的实体参与到多元关系中[11]，超过61%的关系是多元的[12].可以看出，多元关系是一种普遍存在的关系，因此Wen等人[11]提出了知识超图的概念，并证明了通过S2C(star-to-clique)和具体化方法将知识超图转换为知识图谱会导致结构信息丢失.

知识超图能够保存事实间的多元关系，即事实的完整结构信息，因此吸引了研究人员的注意.一个自然而然的想法是将知识图谱中的链接预测模型推广到知识超图中去，例如m-TransH[11]是对TransH算法[13]的推广，m-CP[12]是对CP分解算法[14]的推广，m-DistMult[12]是对DistMult算法[15]的推广.但由于这类模型的原型是专为知识图谱设计的，所以不可避免地导致模型在知识超图上效果表现欠佳.以m-DistMult模型为例，其原型DistMult通过将二元关系表示为对角矩阵，以建模2个实体间的交互.而在知识超图中，m-DistMult仍然使用对角矩阵来表示多元关系，显然一个二维对角矩阵无法建模多于2个实体间的交互，因此m-DistMult在知识超图链接预测任务中效果较差.最近一些研究者们提出基于嵌入表示学习的方法，以解决知识超图中的链接预测问题，这些方法主要分为基于平移(trans-lation)的方法、基于张量分解(tensor decomposition)的方法、基于图神经网络(graph neural network, GNN)的方法以及基于键-值对(key-value pair)的方法.基于平移的方法通常较为简单，但是大多数这类方法不具有完全表达性，即不能准确地将事实(例如：“地球是一颗行星”)与非事实(例如：“地球是一颗恒星”)区分开来[16-17].基于张量分解的方法具有较强的数学理论基础，但通常计算量较大，且需要较多的内存资源.基于图神经网络的方法尽管目前取得了不错的实验效果，但是该类方法是不透明且难以理解的[18].基于键-值对的方法易于理解，但是通常需要确定主三元组及辅助键-值对，目前对于主三元组的确定没有统一标准.

Fig. 1 A toy example of knowledge hypergraph图1 知识超图的简单示例

知识超图通常是有向的，即关系中实体的排列是有序的.图1示例了一个简单的有向知识超图，可以发现：

1) 当同一实体出现在同一关系的不同位置时具有不同角色.例如：当“梁思成”出现在“子女-母亲-父亲”关系的首位时，表示其是“母亲”李蕙仙和“父亲”梁启超的“子女”；当“梁思成”出现在该关系的末位时，表示其是“子女”梁再冰的“父亲”.

2) 当同一实体出现在不同关系中时具有不同角色.例如：当“梁思成”出现在关系“子女-母亲-父亲”和“学生-大学-专业”的首位时，分别表示“子女”和“学生”2个不同的角色.

基于图1的观察，在预测知识超图链接时，考虑实体在不同关系以及不同位置上的角色差异十分重要.然而，现有方法要么没有考虑知识超图的有向性，要么只关注同一关系中不同位置上的实体角色差异[12].

本文提出了一个基于张量分解且具有完全表达性的模型Typer(tensor decomposition for knowledge hypergraph link prediction)，用于解决知识超图中的链接预测问题.Typer模型通过引入角色矩阵以建模实体在不同关系以及不同位置上的角色信息.同时受BoxE[19]的启发，对关系进行细化分解以提升模型性能.此外，为促进实体和关系间的信息流动，本文引入了窗口的概念，令实体和关系在窗口中进行充分交互.在2个大型知识超图数据集上的实验表明，Typer模型能有效处理复杂的多元关系链接预测问题.

本文的主要贡献有3个方面：

1) 提出了一个基于张量分解的知识超图链接预测模型Typer，不仅考虑到实体在不同关系以及不同位置上的角色差异，还对关系进行了细化分解，同时引入了窗口的概念，以增加实体与关系之间的交互.

2) 证明了Typer模型在理论上具有完全表达性，即存在一种嵌入表示能够使模型精确地划分事实与非事实.此外，还给出了Typer模型具有完全表达性时，嵌入表示的维度边界.

3) 在多个公开的真实知识超图数据集上执行了详实的实验，并与其他先进方法进行对比.实验结果和进一步的分析说明了Typer模型对于解决知识超图链接预测问题是有效的，且取得了较其他方法更好的实验结果.

1 相关工作

本节主要介绍知识超图中链接预测的相关工作，这些方法通常被分为4类：基于平移的方法、基于张量分解的方法、基于图神经网络的方法和基于键-值对的方法.

1.1 基于平移的方法

基于平移的方法通常将实体和关系嵌入到同一潜在向量空间中，然后通过关系对实体进行平移，从而学习到实体和关系之间的联系，进而利用学习到的嵌入表示进行链接预测.

TransE[20]是首次提出的基于平移的链接预测方法，对于知识图谱中的任意一个三元组(头实体，关系，尾实体)，其中头实体的嵌入表示加上关系的嵌入表示应近似于尾实体的嵌入表示.由于TransE只能处理二元关系，所以Wen等人[11]提出了m-TransH模型，通过对Trans系列中的TransH[13]进行扩展，用于解决知识超图中多元关系的链接预测问题.随后，RAE模型[21]通过将2个实体共同出现在一个多元关系事实中的概率增加到损失函数中，对m-TransH进行了扩展.

尽管上述基于平移的方法取得了较好的表现，但文献[16]和文献[17]证明了TransE及其一系列变体均不具有完全表达性，在关系建模方面具有局限性.最近，Abboud等人[19]提出了一个基于空间平移的链接预测模型BoxE，该模型将实体表示为低维向量空间中的点，将关系分解为同一向量空间中的一组超矩形，计算实体点到对应超矩形中心的距离，距离越小表示该多元关系事实越可能成立.据我们所知，BoxE是目前唯一一个基于平移且具有完全表达性的链接预测方法.

1.2 基于张量分解的方法

基于张量分解的方法通常将高阶张量分解为多个低阶张量.由于基于张量分解的方法在二元关系链接预测问题中具有较好的表现[22-23]，所以很多研究者将用于知识图谱的链接预测模型扩展到知识超图中，以处理多元关系，例如m-CP[12]和m-DistMult[12]模型分别是对CP[14]和DistMult[15]算法的推广.

最近，Liu等人[24]提出了GETD模型，该模型是对TuckER模型[18]的扩展.然而，GETD模型只能处理k-均匀超图(k-uniform hypergraph)，不能处理同时具有不同元数关系的数据集，即当一个数据集同时具有二元关系、三元关系及其他不同元数关系时，需要先将数据集按照关系元数进行划分，再分别进行训练.GETD是具有完全表达性的模型.Fatemi等人[12]受到SimplE模型[16]的启发，提出了HSimplE模型，该模型能够处理多元关系且具有完全表达性.HypE模型[12]观察到一个实体在同一个关系的不同位置上具有不同角色，因此基于位置为每个实体学习不同的嵌入表示，通过计算对应位置上实体和关系的嵌入表示，获得多元关系事实成立的得分.HypE模型同样具有完全表达性.

1.3 基于图神经网络的方法

图神经网络被证明是一种有效的基于深度学习解决知识图谱中链接预测问题的工具[25].由于图神经网络具有强大的学习能力，一些研究人员将其应用到知识超图中，以解决知识超图中多元关系的链接预测问题.

Yadati[26]提出了G-MPNN模型，通过将信息传递神经网络(message passing neural network, MPNN)推广到知识超图上，解决多元关系的链接预测问题.但是该模型使用双线性评分函数进行评分，导致其对于建模非对称关系具有局限性，同时该模型不具有完全表达性.HGNN模型[27]引入了超边卷积操作，在进行表示学习时，利用超边卷积处理多元关系中实体之间的关联.由于该模型在构建超边时，将实体及其邻居实体视为一条超边，没有考虑多元关系中实体的前后顺序，所以HGNN只能应用于无向超图中.NHP模型[28]采用图卷积网络以解决知识超图上的链接预测问题，但是其忽略了超边的类型，将所有超边视为同一类型，不能有效学习到实体和不同类型关系之间的交互，因此NHP不适用于具有多种关系类型的知识超图.

1.4 基于键-值对的方法

基于键-值对的方法通常将多元关系事实表示为一组键-值对集合，然后根据键-值对中包含的信息评估整个多元关系事实成立的合理性，以完成知识超图中的链接预测任务.

NaLP[29]利用一组角色-值(键-值)对来表示多元关系事实，通过将角色(键)及对应实体(值)的嵌入表示连接起来，送入到卷积层以及全连接层中，获得该事实中所有角色-值对的总体相关性，相关性越大则表明该多元关系事实越可能成立.Rosso等人[30]认为三元组中具有用于链接预测的基本结构信息，仅用键-值对的形式表示多元关系事实会导致次优模型，因此提出了HINGE模型，将多元关系事实表示为一个主三元组和一组辅助键-值对的形式，通过卷积层从主三元组和键-值对中学习相关性特征表示，然后利用最小化操作融合这些相关性特征，再将其送入到全连接层中，获得该事实成立的得分.NeuInfer[31]和HINGE类似，认为多元关系事实中存在一个主三元组，以及一组用于辅助描述主三元组的键-值对，分别计算主三元组的可信性得分，以及主三元组和键-值对的相容性得分，利用加权和获得多元关系事实成立的最终得分.StarE[32]模型利用多元关系事实中前2个实体及对应关系组成主三元组，其余实体用于构成键-值对，通过信息传递网络更新嵌入表示，然后利用Transformer[33]对多元关系事实进行评估.此类方法大多需要确定主三元组，以及设置键-值对中的关键词，而本文方法将多元关系事实视为多元组的形式，与这类方法不同，因此不将本文方法与此类基于键-值对的方法进行对比.

与上述工作相比，本文工作主要致力于解决有向知识超图中的链接预测问题.本文提出的Typer模型不局限于k-均匀超图，能够同时处理具有不同关系元数以及多种关系类型的知识超图，且通过引入角色矩阵显式地为实体在不同关系及不同位置上的角色信息建模.Typer模型将知识超图中的多元关系事实视为多元组，不需要使用额外信息对多元组进行转换.除此之外，Typer模型在理论上具有完全表达性.

2 预备知识

本节讨论知识超图中的链接预测问题，并给出一些基本概念.

定义1.知识超图.知识超图可以表示为G=(V,E).其中V是实体(节点)集；E是V的非空有序元组的集合，称为超边集.超边e∈E对应于一个关系类型映射函数φ(e)∈R，R是关系集合，表明每条超边都对应于一类特定的关系r∈R，关系r的元数|r|是固定的，即关系r涉及的实体个数是固定的.

例1.图1显示了一个知识超图的简单例子，其中共有7个实体，V={梁再冰,林徽因,梁思成,李蕙仙,梁启超,宾大,建筑专业}，3条超边，E={(梁思成,李蕙仙,梁启超),(梁再冰,林徽因,梁思成),(梁思成,宾大,建筑专业)}，2种关系类型，R={“子女-母亲-父亲”,“学生-大学-专业”}，其中φ(梁思成,李蕙仙,梁启超)=φ(梁再冰,林徽因,梁思成)=“子女-母亲-父亲”，φ(梁思成,宾大,建筑专业)=“学生-大学-专业”，关系“子女-母亲-父亲”和“学生-大学-专业”的元数均为3.

在知识图谱中，一个事实通常被表示为三元组(vh,r,vt)，其中vh∈V表示头实体，vt∈V表示尾实体，(vh,vt)∈E，r∈R表示实体间的关系.类似地，在知识超图中，一个事实可以被表示为一个多元组(r,v1,v2,…,vn)，其中r∈R，vi∈V，(v1,v2,…,vn)∈E.

由于知识超图并不能储存所有事实，这里用Tall表示世界中的全部事实集合，对于任意给定的元组(r,v1,v2,…,vn)，若该元组属于Tall，则称该元组为正元组，否则称该元组为负元组.T⊂Tall表示知识超图中的事实集合，T′=Tall-T表示知识超图中缺失的事实集合.给定一个候选元组t∉T，链接预测的目的就是判断该候选元组t是否属于知识超图中缺失的事实，即t是否属于T′.

3 基于张量分解的Typer模型

本文提出的Typer模型主要由3个模块组成：角色信息模块、关系分解模块和交互窗口模块.图2给出了Typer模型的整体架构.

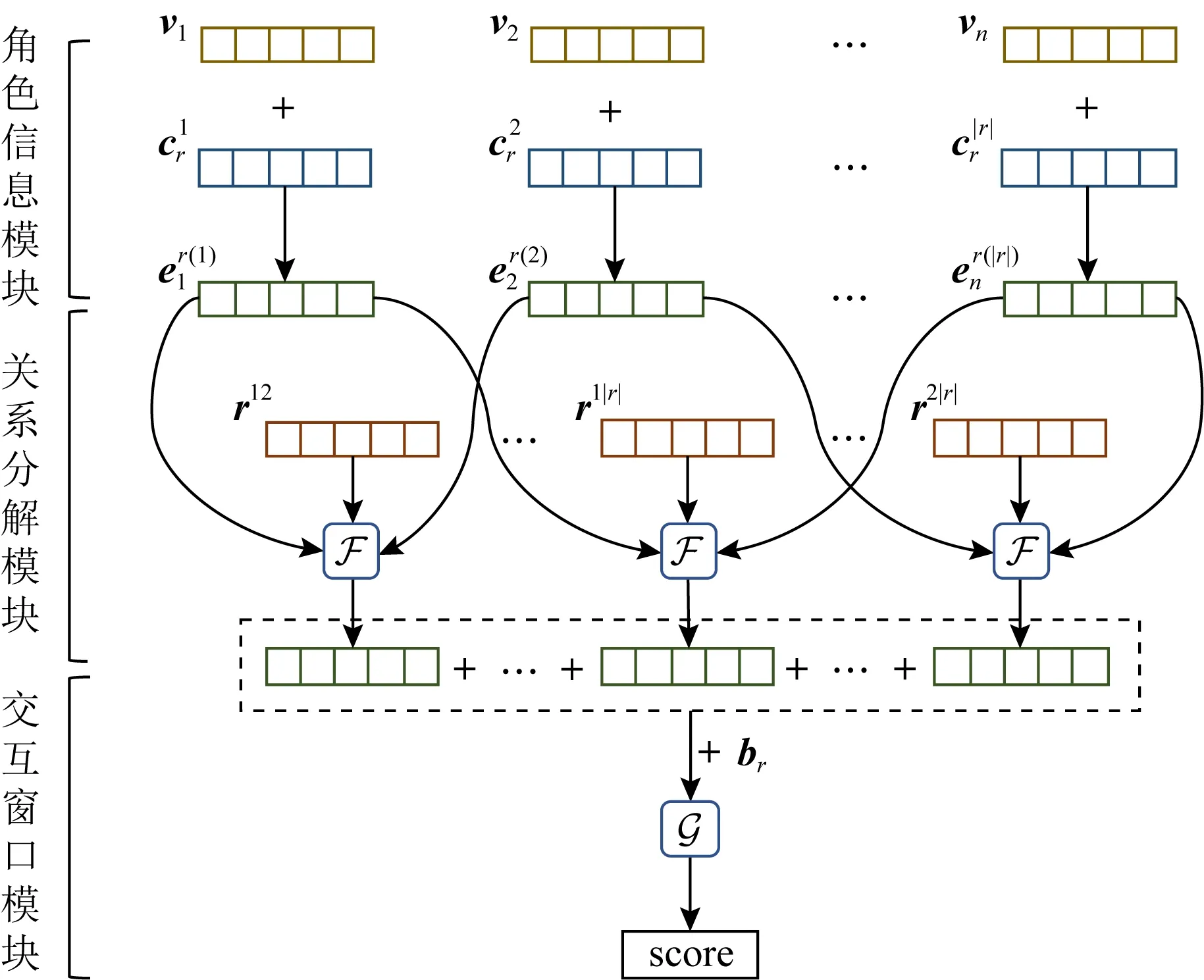
Fig. 2 Architecture of Typer图2 Typer模型的架构

3.1 角色信息模块

由于实体在同一关系的不同位置，以及不同关系中具有不同角色.为显示建模角色信息，这里引入了对应于关系r的角色矩阵cr∈|r|×d，该矩阵的每一行都对应于关系r中一个位置上的角色，即1×d表示关系r位置p上的角色向量.通过将该角色向量与实体本身的嵌入表示向量进行相加，可以使实体在给定的关系和位置中具有特定角色信息.形式化地，给定任意元组t，其对应于关系r，对于该元组中第p个实体vk(由于元组t中第p个实体不一定是vp，为不失一般性，使用vk表示元组t中第p个实体)，其在此元组中的嵌入表示为

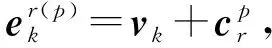
(1)

其中，vk∈1×d是实体vk的嵌入表示，得到的嵌入表示1×d既具有实体本身的信息，又具有关系r中位置p上的角色信息.

3.2 关系分解模块

通常在解决链接预测问题时，关系会被当成一个整体来进行处理，比如HypE,HSimplE等方法.但对关系进行分解会使模型具有更好的表现，比如当前最先进的模型BoxE，其将关系分解为一组超矩形，极大地提升了模型的效果.

给定一个元组t，其对应于关系r，对关系r进行分解后得到多个子关系，每个子关系及其连接的2个实体可以构成一个子三元组(rpq,vi,vj)，其中rpq表示连接元组t中第p个实体vi和第q个实体vj的子关系.为了计算多元组t的最终嵌入表示，首先计算每个子三元组(rpq,vi,vj)的嵌入表示：

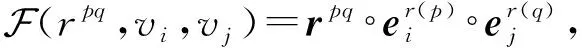
(2)

其中，∘是哈达玛积，rpq∈1×d是关系r对应的子关系rpq的嵌入表示，1×d为具有关系r位置p上角色信息的实体vi的嵌入表示，1×d为具有关系r位置q上角色信息的实体vj的嵌入表示.因为关系r可以分解为个子关系，所以元组t可以生成τ个子三元组.所有子三元组的嵌入表示之和为元组t的最终嵌入表示：

(3)

其中，br∈1×d是对应偏置br的嵌入表示，偏置能够增加模型的灵活性.

3.3 交互窗口模块

由于关系和实体间的交互越多，学习到的嵌入表示越能体现实体和关系间的关联[34-35].为使关系和实体间的交互增多，本文引入了窗口的概念，令实体和关系在窗口中进行充分的信息交互，从而获得每个窗口对元组成立贡献的得分.为方便计算，令窗口大小w为嵌入表示维度d的约数，即d能被w整除，所以窗口数量nw=d/w.经过逐窗口计算后，共获得nw个窗口对于元组t成立贡献的得分，将这些得分加和，即可获得元组t成立的最终得分：

(4)

其中，σ是sigmoid函数，索引[(k-1)w+i]指的是嵌入表示中的第(k-1)w+i个元素.通过非线性函数sigmoid可以使窗口中的实体和关系的信息交互更加充分.

3.4 模型训练

为学习到实体、关系、角色和偏置的嵌入表示，本文使用小批量梯度下降法(mini-batch gradient descent)对模型进行训练.最小化文献[36]中提出的交叉熵损失函数，该损失函数已被证明能有效解决链接预测问题[11-12]：

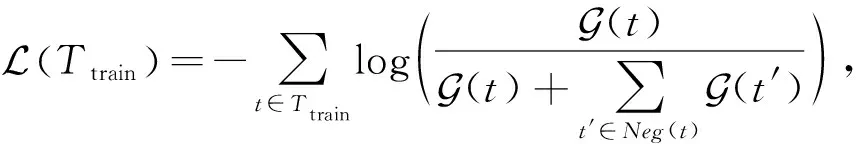
(5)

其中，Ttrain是正元组集合T的训练集，Neg(·)是一个基于给定正元组生成负元组集合的函数.给定一个正元组t，假如负采样率为n，那么对于该正元组中的任意一个实体vi，随机采样n个实体来替换该实体，同时确保生成的负元组t′∉T.通过最小化该损失函数，可以减少模型在链接预测时的误差，从而使模型具有更好的预测表现.算法1给出了Typer模型的伪代码.

算法1.Typer模型.

输出：训练集Ttrain中所有实体嵌入表示v、关系嵌入表示r、角色嵌入表示c、偏置嵌入表示b.

① 利用Xavier均匀分布[37]初始化v,r,c,b;

② fori=1 toNdo

⑤ 生成负元组集合Neg(t);

⑥ fort*∈{t}∪Neg(t) do

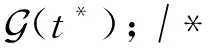
⑧ end for

⑨ end for

4 Typer模型完全表达性分析

本节对Typer模型的完全表达性进行理论分析，并给出当Typer模型具有完全表达性时，嵌入表示维度的边界.

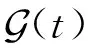
(6)

其中，ε<1/(|T|+2).该评分函数使正元组得分大于等于1-ε，负元组得分小于(|T|+1)ε.由于1-ε和(|T|+1)ε永远不相交，所以该评分函数能够正确划分所有正元组与负元组.因此当Typer模型的评分函数满足式(6)时，其具有完全表达性.

接下来证明Typer模型能够使式(6)成立，这里根据正元组数量，分|T|>0和|T|=0两种情况讨论.

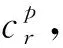
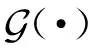
(7)

获得tp在第p个窗口中的得分后，继续计算其在第q个窗口中的得分(q≠p，|T|>1).由于每个正元组对应于一个窗口，所以第q个窗口对应于T中第q个正元组tq.这里分2种情况对tp在第q个窗口中的得分进行讨论，一种是tp和tq对应的关系相同，一种是tp和tq对应的关系不同.

首先讨论第1种情况，由于tp和tq对应于同一个关系，关系元数相同，所以至少有一个实体vi∈tp不在tq中，否则tp=tq，即T中有2个重复的正元组，显然这是不可能的.因此存在z>0个tp中的实体不在tq中，使得这z个实体在窗口q中的嵌入表示元素值为0.因为每个实体都涉及到|r|-1次子三元组得分的计算，所以z个实体共涉及到z×(|r|-1)次子三元组得分的计算.由于在窗口q中，这z个实体的嵌入表示元素值为0，关系r对应的角色嵌入表示的前|r|个元素中存在一个0，导致z×(|r|-1)次子三元组的计算得分减少x.所以tp在第q个窗口中的得分计算为

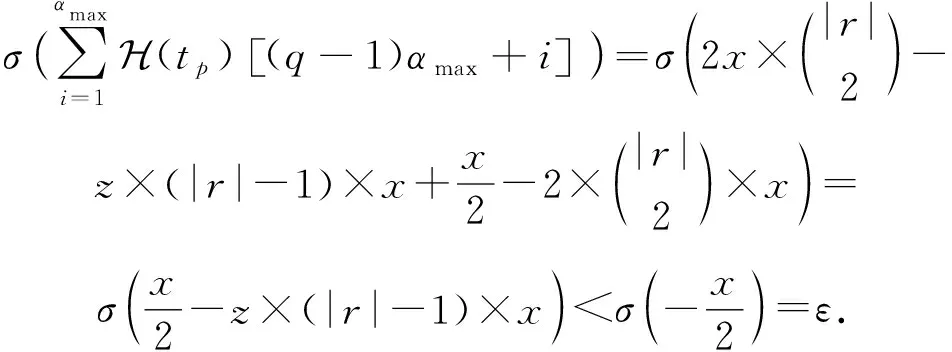
(8)

接下来讨论第2种情况，由于tp对应的关系和tq对应的关系r不相同，所以第q个窗口中r嵌入表示的所有元素值为0，此时tp在第q个窗口中的得分计算为

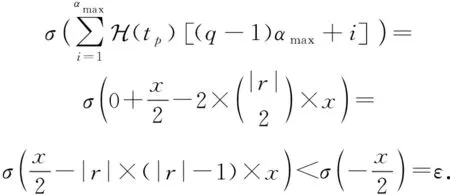
(9)

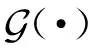
对于任意负元组，根据式(8)和式(9)可知，其所有窗口的得分均小于ε，所以负元组的最终得分必然小于(|T|+1)ε.至此，我们证明了当|T|>0时，Typer模型的评分函数满足式(6).

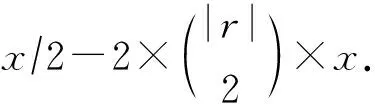
证毕.

例2.为便于理解，图3中给出了该证明的简单示例，其中空方格表示0.在该例子中，共有|T|=3个正元组，即t1，t2和t3，最大关系元数αmax=3.令窗口大小为αmax=3，窗口数量为|T|=3，此时使Typer模型具有完全表达性的嵌入表示维度为αmax|T|=9.

Fig. 3 A toy example of Typer model embedding assignment图3 Typer模型嵌入表示赋值的简单示例

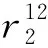
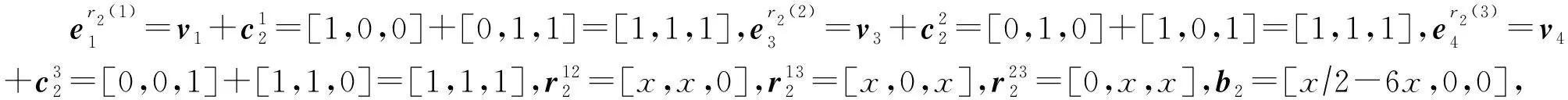
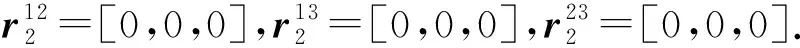
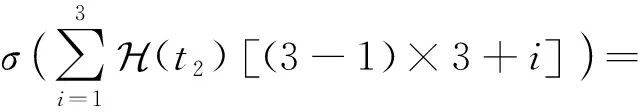
所以正元组t2的最后得分大于1-ε.同理，对于任意负元组，经过上述计算，可以得到每个窗口的得分都小于ε，所以最后总的得分小于3ε，也必然小于(|T|+1)ε=4ε.

5 实 验

本节通过知识超图上的链接预测任务对Typer模型进行有效性验证.我们将实验分为3组以达到不同的实验目的：1)在2个公开数据集上对Typer模型进行有效性实验，并将其与之前的先进方法进行对比，以评估Typer模型的有效性；2)通过消融实验分析Typer模型各模块对模型性能的影响；3)通过参数敏感性实验分析一些重要超参数对模型鲁棒性的影响.在详细说明这些实验前，首先介绍实验中用到的数据集、评价指标以及基线模型和实验设置.

5.1 数据集

本文使用2个公开的真实大型知识超图数据集对Typer模型进行评估：

1) JF17K[11]是基于Freebase过滤得到的，首先删除Freebase中包含出现次数较少的实体的事实，以及涉及字符串、数字及枚举类型的事实，从每个元关系中随机选出10 000个事实，进一步删除包含出现次数少于5的实体的事实，然后利用文献[11]中提出的逆向化方法生成多元组以构成数据集.

2) FB-AUTO[12]也是基于Freebase过滤得到的，移除Freebase中只包含一个实体的事实，以及涉及到数字和枚举类型的事实，按顺序连接具有相同关系和头实体的事实，构成多元组，从中选择头实体标签为“automotive”的事实构成此数据集.

由于JF17K中没有验证集，所以本文使用与文献[12]和文献[16]相同的训练、验证、测试集设置，即从JF17K的训练集中随机选取20%作为验证集.JF17K和FB-AUTO数据集的详细统计信息如表1所示：

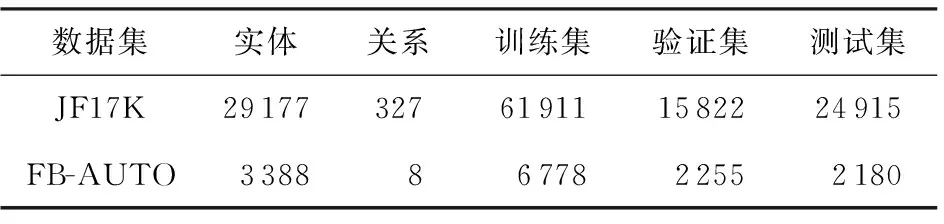
Table 1 Statistics of Datasets表1 数据集的统计信息

5.2 评价指标

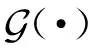
(10)

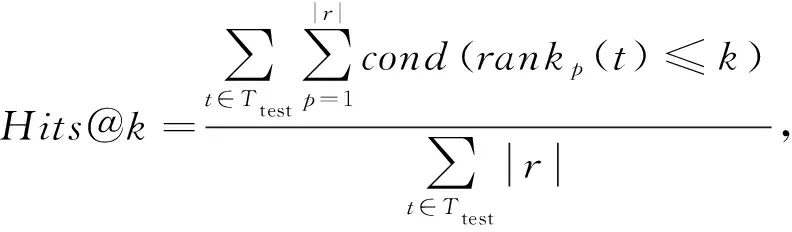
(11)

其中，r是正元组t对应的关系，cond(·)是条件函数，当条件成立时值为1，否则值为0.MRR和Hits@k值越大表明模型性能越好.

5.3 基线模型和实验设置

为公平比较，本文只考虑那些能够处理具有不同元数关系的数据，且不需要额外信息辅助的模型作为基线模型.因此选择如下模型作为本文的基线模型：

1) m-DistMult[12].对DistMult算法[15]进行了扩展，通过计算多元关系事实中所有实体和关系嵌入表示的哈达玛积的元素和，获得多元关系事实成立的得分.

2) m-CP[12].对CP算法[14]进行了扩展，通过赋予一个实体多个嵌入表示，以建模同一实体在不同位置上的角色信息.

3) m-TransH[11].对TransH算法[13]进行了扩展，通过将实体嵌入表示映射到对应关系的超平面上，以建模同一实体在不同关系中的角色信息.

4) HSimplE[12].将实体嵌入表示视作该实体基于不同位置嵌入表示的连接，对嵌入表示中的元素移动，即可获得实体基于不同位置的嵌入表示.

5) HypE[12].通过使用多个卷积核获得实体在不同位置上的嵌入表示，对卷积后的实体嵌入表示和关系嵌入表示的哈达玛积求元素和，即为多元关系事实成立的得分.

6) BoxE[19].将实体映射到潜在向量空间中，基于同一向量空间将多元关系分解为多个显式超矩形，通过计算实体嵌入表示相对于超矩形的位置，获得多元关系事实成立的得分.

本文与所有基线模型公开的最好结果进行对比.由于BoxE使用的排名方法与其他基线模型不同，为公平比较，将其改为其他基线模型中使用的排名方法，然后进行对比实验.此外，也给出了Typer模型在BoxE排名方法下的对比实验结果.

我们利用PyTorch[38]实现Typer模型，并通过Adam优化器[39]进行优化.实验默认参数设置如下，嵌入表示维度为200，负采样率为10，训练次数为1 000，批大小为128，学习率为0.1，窗口大小为2，验证检查点为100，选择在验证集上MRR指标表现最好的模型进行测试.

5.4 有效性分析

表2给出了Typer模型和其他先进模型在数据集JF17K和FB-AUTO上的对比实验结果.实验结果表明，本文提出的Typer模型在2个知识超图数据集上的所有评价指标均超过了基线模型.更具体地说，就MRR指标而言，Typer模型相较于HypE在数据集JF17K和FB-AUTO上分别提升了6.88%和8.83%.在FB-AUTO数据集中，Typer模型Hits@3指标的结果已经超过了所有基线模型Hits@10指标的结果，表明了Typer模型能够有效完成知识超图中的链接预测任务.

Table 2 Results of Link Prediction表2 链接预测结果

根据实验结果可以发现，像m-DistMult和m-CP这类直接将二元关系链接预测模型推广到多元关系上的模型实验效果并不好，说明对于多元关系链接预测问题，需要根据其特点进行针对性设计，多元关系链接预测问题与二元关系链接预测问题并不完全相同.HSimplE和HypE结果低于Typer的主要原因是由于二者均将关系视为一个整体，且没有考虑到同一实体在不同关系中具有不同角色.通过对实验结果的分析，Typer模型表现较好的主要原因是其不仅考虑到实体在不同关系以及不同位置上具有不同角色，而且对关系进行了细化分解，还引入了窗口的概念，使实体与关系间的交互增多.

由于BoxE使用了不同的排名方法，所以为了公平比较，这里在FB-AUTO数据集上使用BoxE的排名方法对Typer模型性能进行评估，其中窗口大小设为1，其余参数保持不变，实验对比结果如图4所示.从图4给出的结果可以看出，本文方法在各项指标上都超过了BoxE.此外，BoxE在不同排名方法下，模型性能相差很大，就MRR指标而言，实验结果相差为0.352.而本文方法各项指标基本保持稳定，MRR指标上的实验结果相差仅有0.002.表明Typer模型能够很好地学习到实体与关系间的交互，所以在不同排名方法下仍然保持性能稳定.

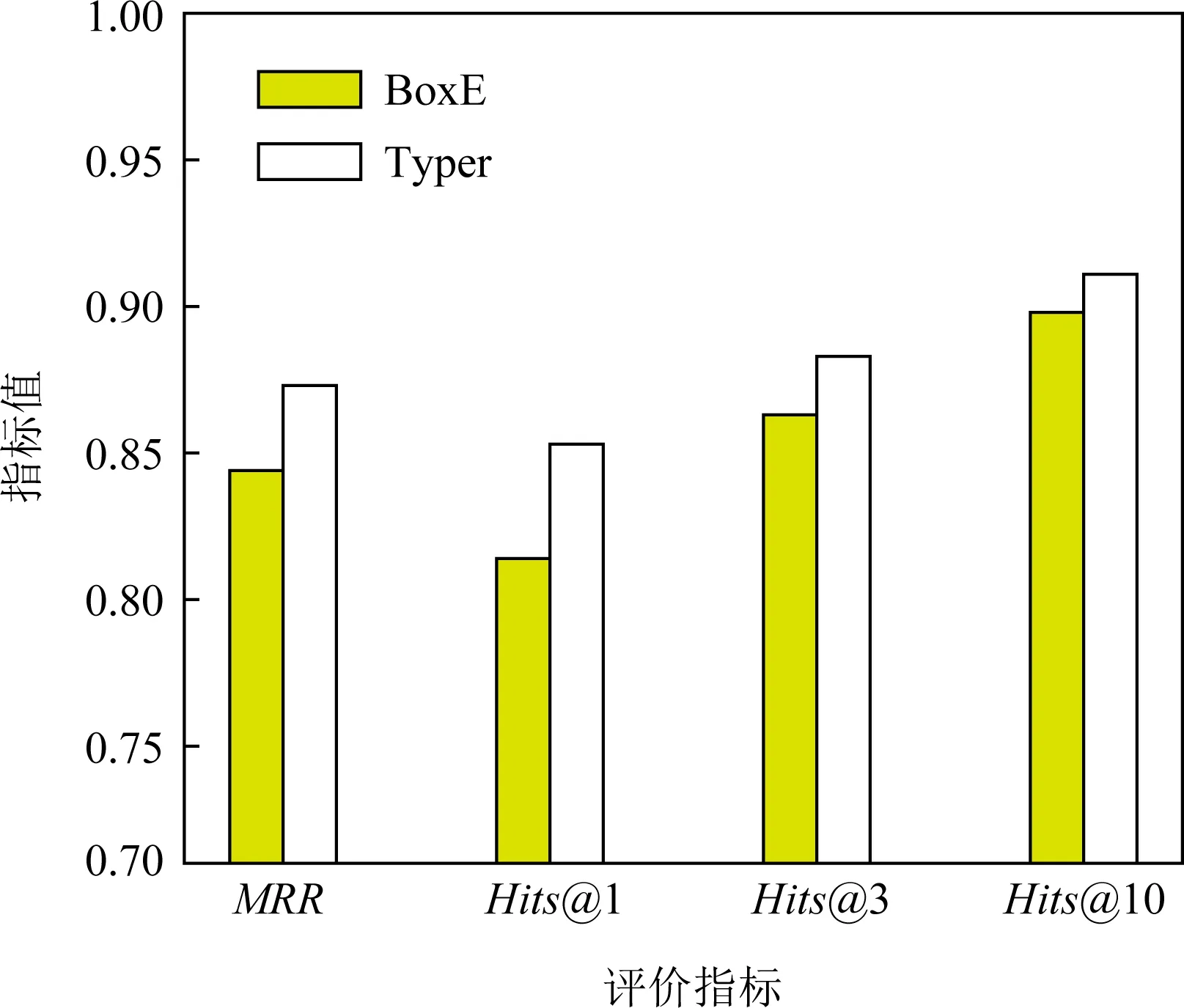
Fig. 4 Comparison of Typer and BoxE on FB-AUTO图4 Typer和BoxE在FB-AUTO数据集上的对比

为了深入研究Typer模型在处理不同元数关系时的差异，首先将FB-AUTO测试集中的数据按照关系元数进行划分，其中包含764个二元关系、44个四元关系以及1 372个五元关系.然后令Typer模型分别在这3个具有不同元数关系的数据集上进行测试.表3给出了Typer模型及基线模型关于MRR及Hits@10指标的实验对比结果.从实验结果中可以看出Typer模型在所有元数关系上均超过了基线模型.这表明Typer模型不仅能够很好地处理具有更高元数的关系，在处理二元关系时同样具有优势.

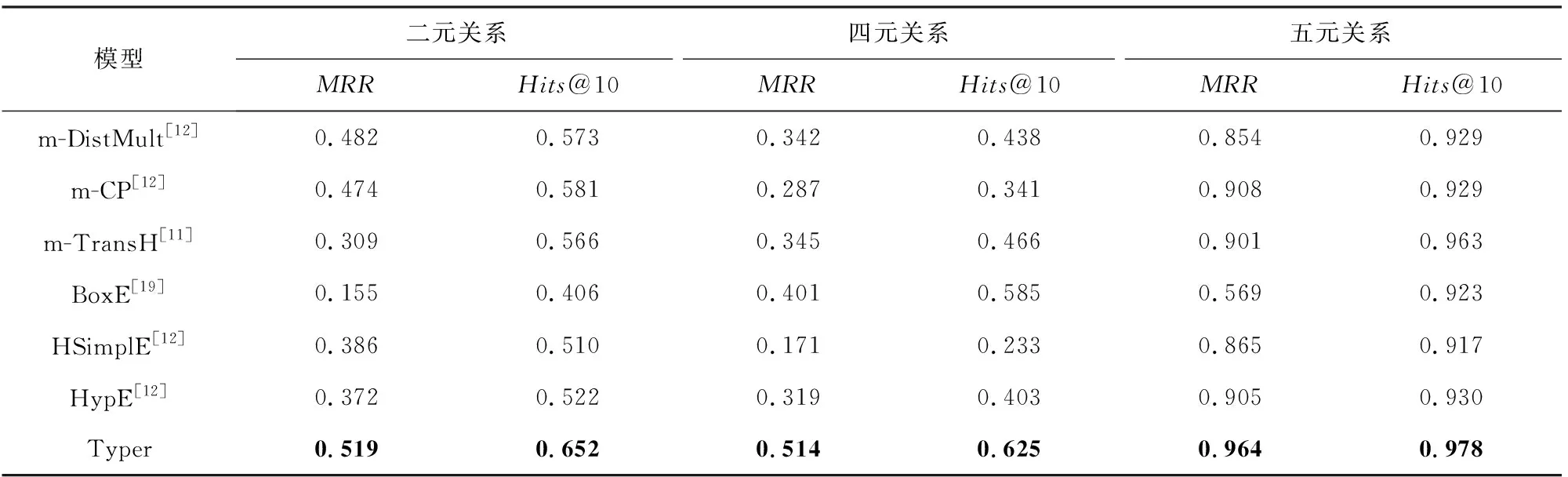
Table 3 Results of Link Prediction for Relations with Different Arities表3 具有不同元数关系的链接预测结果

5.5 消融实验

为验证各模块对模型性能的影响，本文基于Typer模型设计了3个变体，即Typer-Role，Typer-Rel以及Typer-Win，分别表示在Typer模型的基础上移除了角色信息模块、关系分解模块以及交互窗口模块.Typer模型及其3个变体在FB-AUTO数据集上的实验对比结果如表4所示：

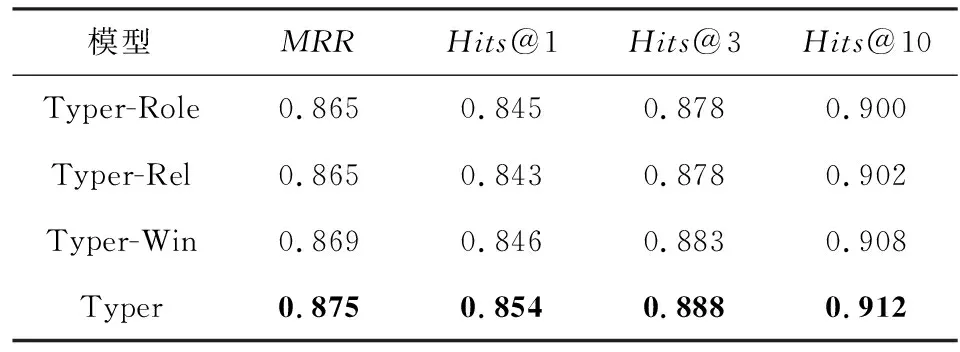
Table 4 Results of Ablation Experiments on FB-AUTO表4 FB-AUTO数据集上的消融实验结果

观察表4，可见Typer模型在各项指标上均优于其3个变体.具体地，就MRR指标而言，Typer模型相较于变体Typer-Role，Typer-Rel以及Typer-Win分别提升了1.16%，1.16%以及0.69%.显然缺少任何一个模块都会使得模型效果变差，这表明Typer模型的3个模块能够很好地捕捉到实体与关系之间的交互.更重要的是，缺少其中任何一个模块都不能保证Typer模型仍然具有理论上的完全表达性.

5.6 参数敏感性分析

为研究Typer模型的鲁棒性，本文在FB-AUTO数据集上进一步分析了一些重要超参数对模型性能的影响，包括嵌入表示维度d、负采样率n以及窗口大小w.令嵌入表示维度d∈{50,100,150,200,250,300,350,400}，负采样率n∈{1,5,10,15,20}，窗口大小w∈{1,2,4,5,8,10,20}.为实验公平，除当前研究的超参数外，其余超参数均与5.3节实验设置中相同，实验结果在图5中给出.

图5(a)显示了Typer模型在不同嵌入表示维度下，各项评价指标的变化趋势.从图5可以看出，当嵌入表示维度小于200时，随着维度的增加，各项指标呈上升趋势；而当维度到达200时，各项评价指标逐渐达到平稳；表明当嵌入表示维度超过200时，Typer模型是相对稳定的.

图5(b)显示了Typer模型在不同负采样率下，各项评价指标的变化趋势.从图中可以看出，负采样率对Typer模型的影响不大.因此，就负采样率而言，Typer模型是稳定的.

图5(c)显示了Typer模型在不同窗口大小下，各项评价指标的变化趋势.从图中可以看出，当窗口大小开始增加时，实验结果中各项指标均有所提升，表明增加实体与关系间的交互有助于模型性能的提升；但随着窗口大小进一步增大时，各项指标开始下降，表明过多的交互可能对模型学习无益.因此，窗口大小对模型Typer而言是一个敏感的超参数，需要根据数据集对窗口大小进行仔细调整以使模型发挥出最佳效果.

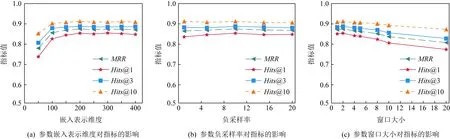
Fig. 5 Parameter sensitivity analysis图5 参数敏感性分析

6 总结与展望

本文提出了一个用于解决知识超图链接预测问题的张量分解模型Typer，并证明了该模型在理论上具有完全表达性.Typer模型不仅考虑到实体在不同关系以及不同位置上具有不同角色，还考虑到对关系进行细化分解有助于提升模型性能.此外，Typer模型引入了窗口的概念，以增加实体与关系间的信息流动.在2个大型公开知识超图数据集上进行的详实实验说明了Typer模型的有效性和先进性.

下一步，计划研究将背景知识(例如规则等)注入到模型中，以及融合多模态数据以进一步提升模型性能的方法.此外，基于张量分解的方法虽然具有数学理论支持，且有着较为广泛的学习研究，但是其计算量较大，训练推理时间较长，无法做到实时链接预测，所以后续计划尝试采用并行计算的方法来加速模型的训练和推理.同时，还计划探索Typer模型在现实中的应用，我们认为将其扩展到大规模数据集上也是一个有趣的研究方向.