基于啁啾补偿的自相似脉冲压缩光栅对的设计
李沐霖,张巧芬,史圣达,庞亮雨,高梓皓
(广东工业大学 a.机电工程学院; b.精密微电子制造技术重点实验室,广州 510006)
0 引 言
超短脉冲在信息的超速获取、半导体纳米结构的研究、生物医疗[1-2]和信息高速传输等方面都有重要应用,获取优质的超短脉冲光源一直都是光纤光学研究领域的热点话题。近年来针对该问题,国内外学者提出了一系列行之有效的方案,包括通过色散补偿光纤[3-4]、光栅对[5]和啁啾光纤光栅[6]等色散补偿器件或利用光脉冲在光纤中的孤子效应[7]和交叉相位调制效应[8]进行光脉冲压缩,从而获得优质的超短脉冲。其中光栅对因其结构简单、色散补偿量大且可以灵活调节等优点在光脉冲压缩领域得到了广泛应用。为了保证压缩质量,在利用光栅对压缩前,需要保证脉冲在整个宽度上具有强线性啁啾,通常的做法是使脉冲通过一段带有正色散的光纤,但光纤中的非线性作用会导致脉冲输出频率啁啾线性范围较窄、线性度较差,严重影响了光栅对的压缩质量。对此,国外的Kruglov V I[9]等人和国内的Zhang Q F[10-11]等人提出的自相似脉冲能很好地解决该问题。所谓自相似脉冲是指在群速度色散(Group Velocity Dispersion, GVD)和自相位调制(Self-Phase Modulation, SPM)及增益的共同影响下,产生能量被显著放大、具有很强线性啁啾和时域形状类似抛物线型的脉冲。本文利用色散渐减光纤(Dispersion Decreasing Fiber, DDF)产生自相似脉冲,然后利用光栅对对自相似脉冲进行啁啾补偿压缩,意在获取优质的超短脉冲光源。
1 DDF产生自相似脉冲
当光脉冲宽度>5 ps时,光脉冲在光纤中传输的高阶色散和高阶非线性效应相对较小,因此光脉冲在DDF中的传输方程可由下面的非线性薛定谔方程描述[12-13]:
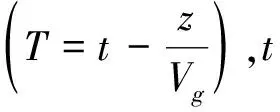
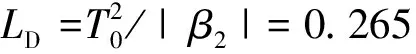
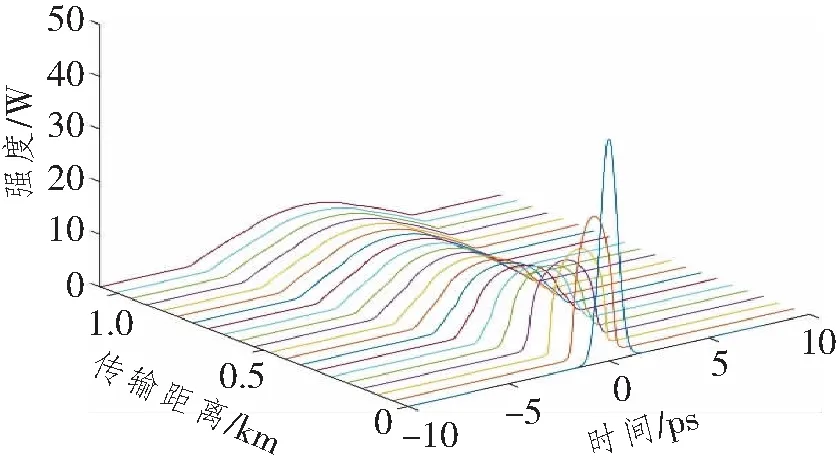
图1 时域波形演化图
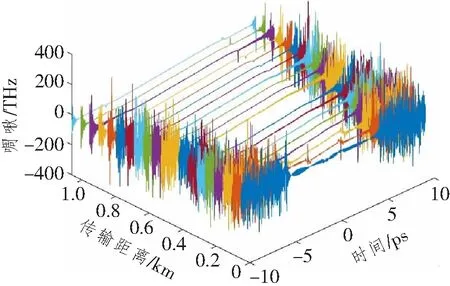
图2 频率啁啾演化图
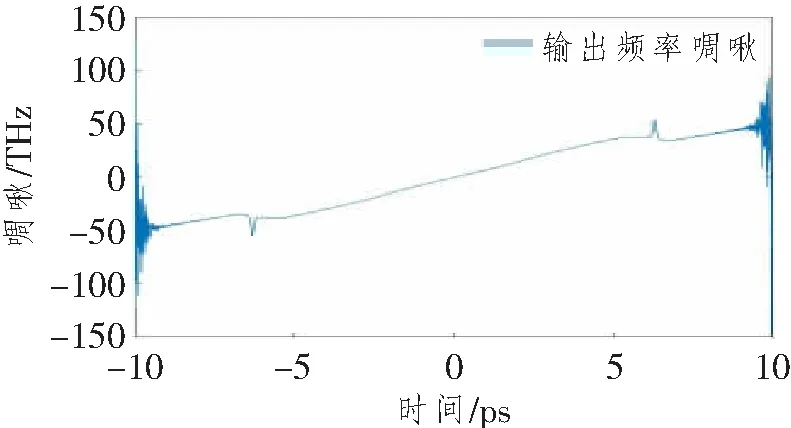
图3 输出脉冲频率啁啾分布图
由图1可知,初始高斯脉冲在时域内波形不断展宽,其原因是电磁波与电介质的相互作用导致折射率n(w)对频率w的响应不同,在同一个电介质内,脉冲的不同频率分量移动的速度不同,在正常色散区(β2)内,高频(蓝移)分量会比低频(红移)分量移动的慢,从而导致低频分量在到达终点时比高频分量快,随着传输距离的增大,这种差距会越来越明显,最终会形成图1所示的时域波形展宽现象。同时,由图2可知,随着脉冲感应出的频率啁啾随着光纤长度的增加,线性区域会明显扩大,脉冲两侧的边缘震荡也会逐渐减小。当光纤长度达到4倍LD时,如图3所示,此时脉冲有很宽的线性啁啾范围,SPM效应所感应出的非线性啁啾在整个脉冲范围内几乎被正常GVD效应线性化,可认为此时脉冲已完成了自相似演化。
2 利用光栅对压缩自相似脉冲
当光脉冲入射到光栅对的一个光栅时,不同频率分量w经过光栅后衍射角θ(w)不同,从而存在不同的时间延迟,蓝移分量会比红移分量提前到达,当具有正线性啁啾的自相似脉冲进入光栅对时,自相似脉冲中原来速度较慢的蓝移分量会逐渐赶上原来速度较快的红移分量,此时的光栅对就好比一段具有负色散的光纤,通过调整光栅对的参数,就能达到脉冲压缩的目的。具体数学分析如下。
脉冲通过光栅对时,不同的频率分量会产生不同的时间延迟,因此不同频率分量在经过光栅时会产生不同大小的相移,频率w所获得的相移可表示为
式中:Lp(w)为频率为w的脉冲分量移动的光程长度;c为光在真空中的速度。由图4通过几何关系可知Lp(w)为
式中:α为入射角;d为光栅间距;L1和L2为脉冲经过光栅对的两段光程长度,如图4所示。
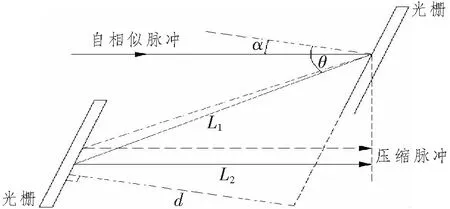
图4 光栅对压缩示意图
当实际脉冲宽度远大于中心频率w0时,可将相移φ(w)在w0处进行泰勒级数展开:
式中:φ0为常数;φ1与通过光栅对的时间有关;φ2和φ3分别为光栅对的色散效应。当脉冲的谱宽远小于w0时,φ3和更高次项部分色散效应的影响相对φ2小的多,可以忽略不计,如果再同时忽略不重要的常数项φ0和线性项φ1,则自相似脉冲在光栅对中产生的相移仅由φ2决定。
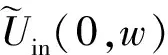
由色散补偿原理[15]有:
式中:D1为DDF的二阶色散总量;D2为光栅对提供的补偿二阶色散总量。通过数值模拟可得脉冲经过DDF后产生的正常二阶色散总量为D1=-0.134 7 ps-2,为了补偿脉冲经过DDF后产生的正常二阶色散总量,应调整光栅对的各项参数使得光栅对提供的补偿色散总量为0.134 7 ps-2。取光栅对的光栅周期Λ为1 μm,设自相似脉冲经过光栅对的入射角为α,衍射角为θ,当色散完全补偿时,α与θ和光栅间距d的关系如图5和6所示。
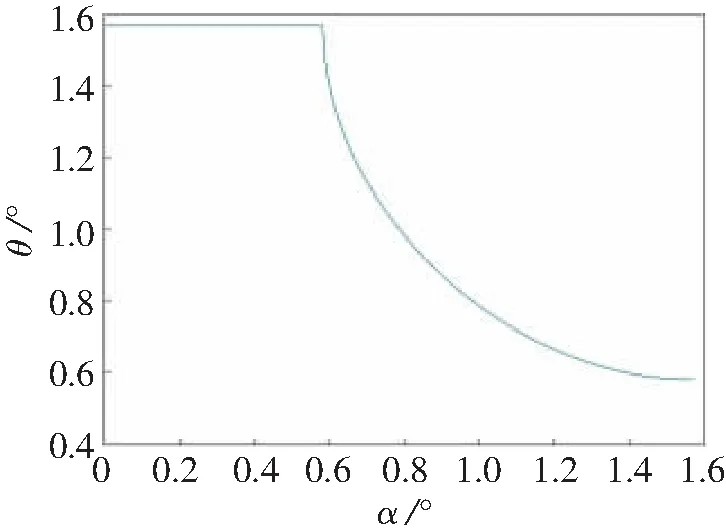
图5 α与θ关系示意图
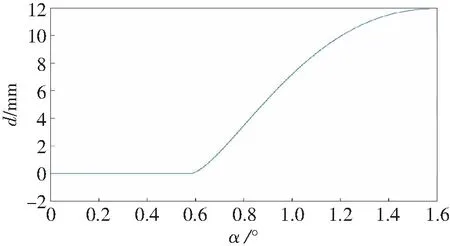
图6 α与d关系示意图
理论上,图5和6中的每一对入射角α、衍射角θ和与之对应的光栅间距d都能够实现对自相似脉冲压缩的目的,但随着d的增大,自相似脉冲的能量会显著衰减,同时为了增大光栅的衍射效率需要保证α接近于闪耀角(Littrow)[16],即保证|α-θ|绝对值要小。本文选取α=55 °,θ=46.96 °,d=6.50 mm,其光栅对压缩的数值模拟结果如图7所示。
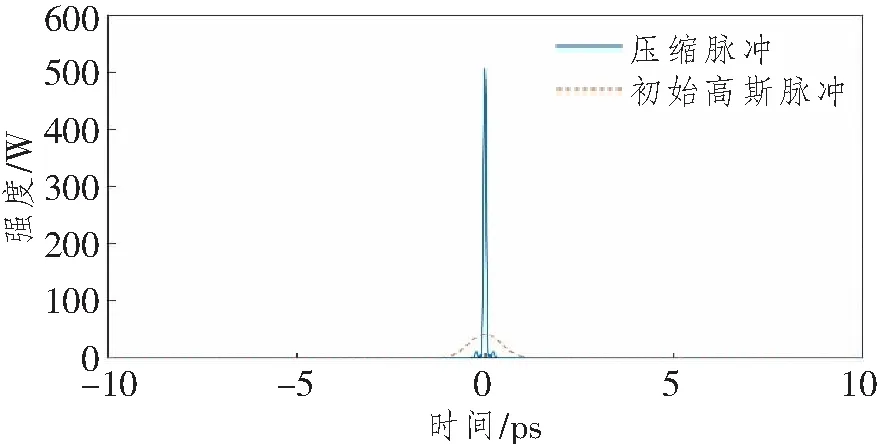
图7 压缩脉冲时域波形图
如图所示,压缩脉冲的峰值功率为507.6 W,压缩FWHMTFWHM为80 fs。为了衡量光栅对对自相似脉冲的压缩质量,我们定义归一化压缩品质参量Q:
式中:Pout为压缩脉冲的输出峰值功率;pin为输入高斯脉冲的峰值功率;压缩因子F=TFWHM/T0。显示,Q越大则脉冲压缩的质量越好,对于一个峰值功率确定的输入脉冲,为了提高脉冲的压缩品质,往往会导致脉冲F的降低。因此,衡量一个脉冲压缩系统的好坏,不仅要得到高的压缩因子F,还要保证具有较高的输出峰值功率。通过计算可知,光栅对对自相似脉冲进行压缩的Q为0.96、F为12.5时,压缩质量较为理想。
3 三阶色散对光栅压缩的影响
脉冲在光纤中传输的色散效应主要受二阶色散影响,这是由于光纤的脉冲频谱宽度远大于中心频率,导致高阶色散效应相比于二阶色散小得多。当入射脉冲波长在光纤的零色散波长附近或脉冲的宽度<1 ps时,高阶色散的影响就不能忽略了。考虑三阶色散时,式(2)变为以下形式:
式中,β3为三阶色散参量。等号右边3项分别为光纤中的二阶色散、三阶色散和非线性效应。取三阶色散系数为1×10-3ps3/km,通过数值模拟得到初始高斯脉冲经过DDF后脉冲演化的时域波形和输出频率啁啾,分别如图8和9所示。

图8 考虑三阶色散时初始高斯脉冲经过 DDF后输出脉冲时域波形图
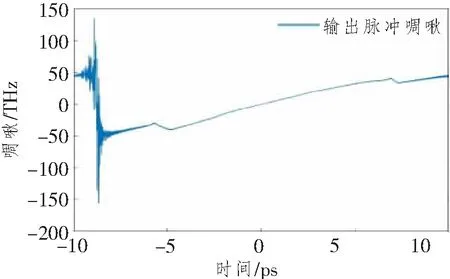
图9 初始高斯脉冲经过DDF后 输出脉冲频域啁啾分布图
由图8和9可知,由于三阶色散的作用,自相似脉冲的时域波形和输出频率啁啾变得不再对称,输出峰值功率略微向原点左侧移动,输出频率啁啾的线性范围仍然保持得较宽,但频率啁啾中心略微向原点右侧移动。将该自相似脉冲以同样的入射角进入光栅对,通过数值模拟得到最终的压缩脉冲输出峰值功率为213.1 W,输出FWHM为130 fs,压缩品质参量Q仅为0.67,压缩因子F为7.5,压缩脉冲时域波形图如图10所示。
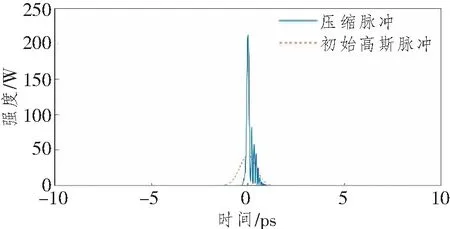
图10 考虑三阶色散时压缩脉冲时域波形图
由图可知,在三阶色散的影响下,压缩脉冲的时域波形产生了畸变,在时域波形的右侧出现了大量的基座,导致了输出脉冲功率的降低,严重影响了脉冲的压缩质量。通过分析式(9)、结合式(8)以及光栅的衍射公式可得,光栅对提供的有关三阶色散参量φ3为
可见φ3≥0,因此光栅对产生的是正的三阶色散,无法为脉冲提供负的三阶色散补偿,因此当三阶色散参量较大时,则必须要考虑三阶色散对光栅对压缩性能的影响,为了探究三阶色散效应的大小对光栅对压缩质量的影响,我们保持输入脉冲不变,DDF的二阶色散β2不变,改变三阶色散β3的取值,使β3从0增加到1×10-3ps3/km,间距为5×10-5ps3/km,同时保持光栅对的各参数不变,通过数值模拟得到不同β3值时脉冲的Q值,通过曲线拟合得到Q随β3变化的关系如图11所示。
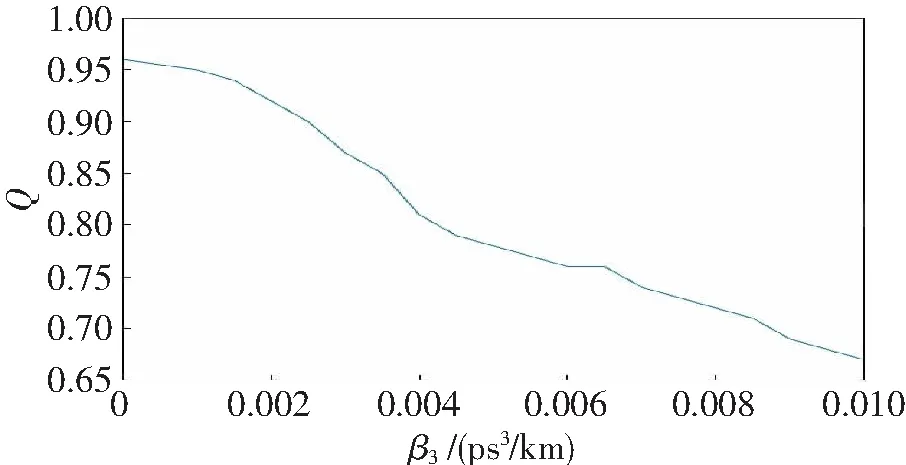
图11 Q与β3的关系图
由图可知,随着β3的增大,光栅对的Q值不断降低,因此要提升自相似脉冲-光栅对压缩质量,必须保证光纤中的β3足够小。在本系统中,若要保证Q>0.9,则DDF中的β3应<2.5×10-4ps3/km。
4 结束语
本文将自相似脉冲与光栅对结合,利用DDF产生具有宽线性范围和强线性啁啾特性的自相似脉冲,然后利用光栅对自相似脉冲进行压缩,最终得到了峰值功率为507.6 W、压缩FWHMTFWHM为80 fs的超短脉冲,压缩比为12.5,Q为0.96,F为12.5。在此基础上,我们分析了三阶色散对该压缩系统的影响,当DDF中的三阶色散参量为1×10-3ps3/km时,得到压缩脉冲的峰值功率为213.1 W,FWHM为130 fs,Q为0.67,F为7.5。随后通过进一步分析发现,随着三阶色散的增大,光栅对压缩质量Q会显著降低。

