方柱间液气交界面形状研究

张万秋，谭栋文，周新平,2

(1.华中科技大学，湖北 武汉 430074； 2.浙江大学 流体动力与机电系统国家重点实验室，浙江 杭州 310027)

毛细现象在自然界较为常见，比如：水黾水面行走、植物种子漂浮、浮萍聚集；在工业界也有着比较广泛的应用，比如：喷洒反湿润喷雾防止眼镜和车窗上的水汽遮挡视线、油墨打印技术、毛细光刻技术等。在表面张力作用下液体会在固体表面变形[1-5]，固体周围液气界面形状由颗粒重力、毛细力、液体压力决定，与其表面接触角、密度、尺寸形状有关。当两个固体颗粒逐渐靠近时，它们之间存在相互作用力，每个颗粒周围的液气界面形状也在不断的改变，在能量最小时达到平衡状态。

多个固体在液面上时，液体表面因变形产生的毛细作用力会制约固体的自由运动。固体之间液气交界面形状决定了两者之间的相互作用力。Uzi等[6]基于线性叠加假设，研究了漂浮颗粒之间的横向毛细作用力。Sasai[7]基于线性公式求解了漂浮在熔融态钢液表面上的三氧化二铝渣粒之间的毛细吸引力。Danov和Kralchevsky[8]基于线性假设开展了毛细多极子理论研究工作。然而，线性化处理在不满足小坡度假设的情况下可能会导致结果的失真，最小能量法可以避免这个问题。Dushkin[9]研究了两个圆柱(圆球)之间的毛细受力情况，使用线性化方法简化杨-拉普拉斯方程，略去非线性项。Raufaste等[10]则基于最小能量法计算了倾斜圆柱的液气交界面形状，使用最小能量法在结果上等价于求解完全的杨-拉普拉斯方程，具备较好的精度。对于方柱弯月面形状的研究还比较缺乏，本文使用最小能量法，研究两个方柱间液气交界面的形状随着放置方向、间距、接触角、邦德数的不同而变化的情况，在方法上具备良好的精度，能对研究方形物体的弯月面形状带来一定的启示。

1 模型

当液体润湿固体表面时，系统的总能量W包括重力势能Wg、液体表面能Wm和壁面润湿能Ww。稳定的弯月面构型在系统总能量最小的时候取得。可以采用变分法推导出非线性的杨-拉普拉斯方程，但一般情况下该非线性弯月面方程难以求解，为了计算简便，常采用基于线性化假设的处理方法。也可以通过直接数值求解系统的最小能量来找到对应的弯月面构型。本文采用有限元软件Surface Evolver(SE)[11]进行数值求解，得到系统最小能量对应的弯月面构型。重力势能Wg为体积分形式，而液体表面能Wm和壁面润湿能Ww都为面积分形式。在SE中，将系统的重力势能项Wg从体积分形式转化为面积分形式，而对于壁面润湿能项Ww，将其从壁面处的面积分形式转化为线积分形式。

采用SE计算时，需要确定计算域的几何条件，进行网格划分，并对点、线、单元按一定的顺序和方向编排序号。定义方柱中轴与x轴(水平方向)的夹角为方位角α。图1所示为两柱方位角都为0°(两方柱边对边放置)条件下计算域网格划分示意图。图1中：线段1、2、3、4和5、6、7、8分别表示两个方柱的壁面边界线，需要根据方柱的形状参数设定几何约束；线段9、10、11、12为计算域远场的边界，无须设置几何约束。编写相关文件并运行计算，可以得到弯月面最终构型。

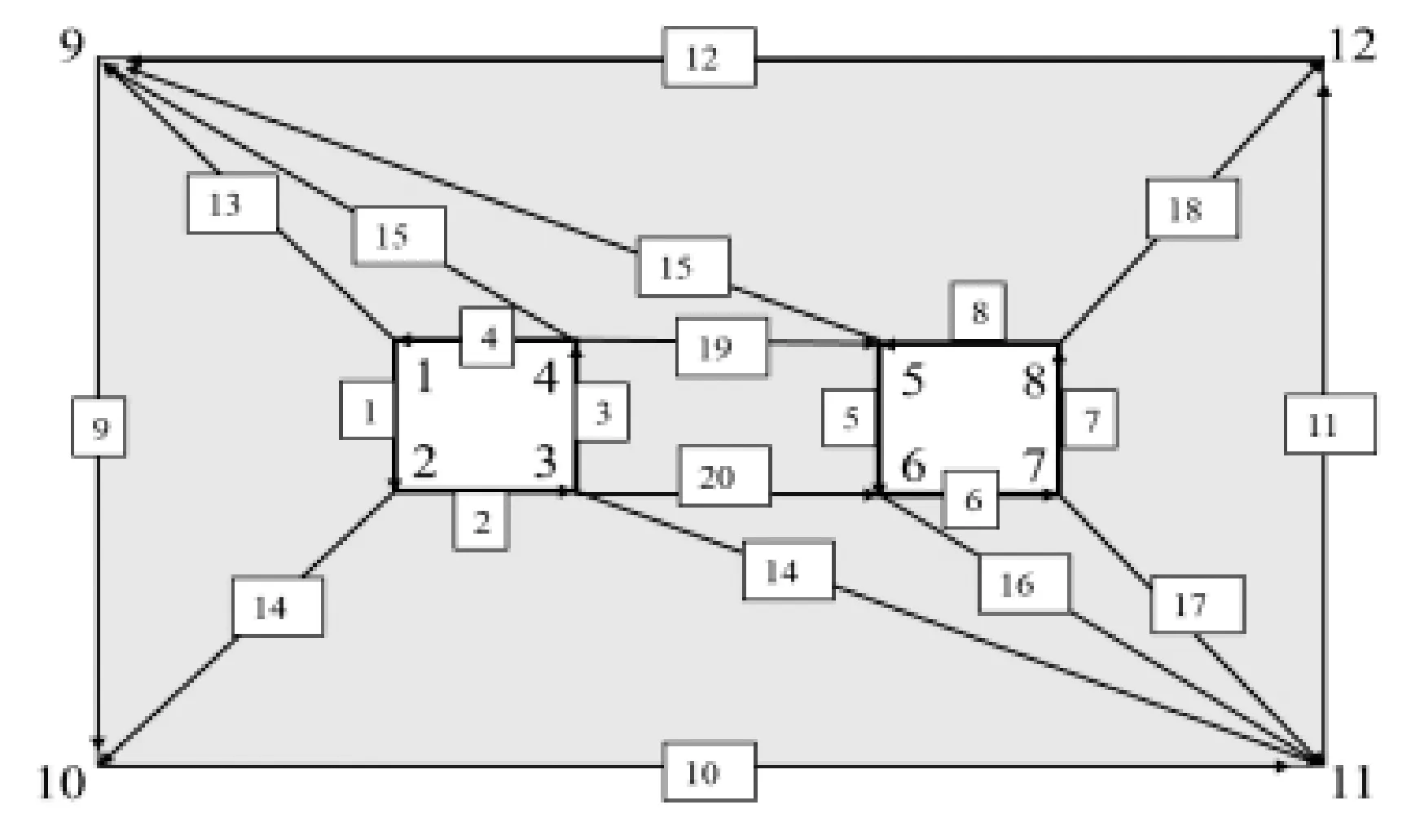
图1 当两个方柱的方位角α=0°时的计算域网格划分示意图

通过改变几何或物理参数，如方柱中心间距D、方位角α、接触角θ和重力加速度g，可以得到不同条件下的弯月面构型。以标准状况下的水为研究对象，水密度ρ=1 000 kg/m3，表面张力系数γ=0.072 N/m，并假设两个方柱具有相同的条件，即具有相同的边长、方位角和固液接触角，并令边长为固定值L=2.7 mm，定义无量纲参数邦德数Bo=ρgL2/γ来表征重力加速度的变化。

2 结果与讨论

当SE计算收敛时，所形成的稳定弯月面构型如图2所示。根据主视图，弯月面高度变化类似于一个马鞍形，关注“马鞍”的中点，令方柱中心线连线中点的弯月面高度为Hm，并观察Hm随不同参数的变化。SE计算收敛时的结果如图2所示。当两个方柱的对应对称轴之间的夹角改变时，弯月面形状也将随之改变。

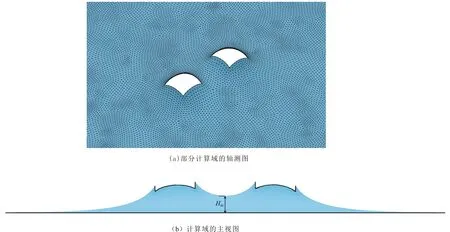
图2 当α=0°，θ=30° D=2.5 L，Bo=1时的SE计算结果

图3比较了α=0° (边对边放置)和α=45°(尖对尖放置)两种条件下Hm随D的变化。由图3可以看出：随着方柱逐渐靠近，中心高度增加；方柱间距足够远时，对两个方柱之间弯月面中心高度的影响较小。随着两方柱逐渐靠近，两者之间的毛细作用变强，中间自由面的凸起变大；另外，在两方柱间距较小的情况下，与α=0°条件相比，α=45°条件下的Hm有明显的增加。

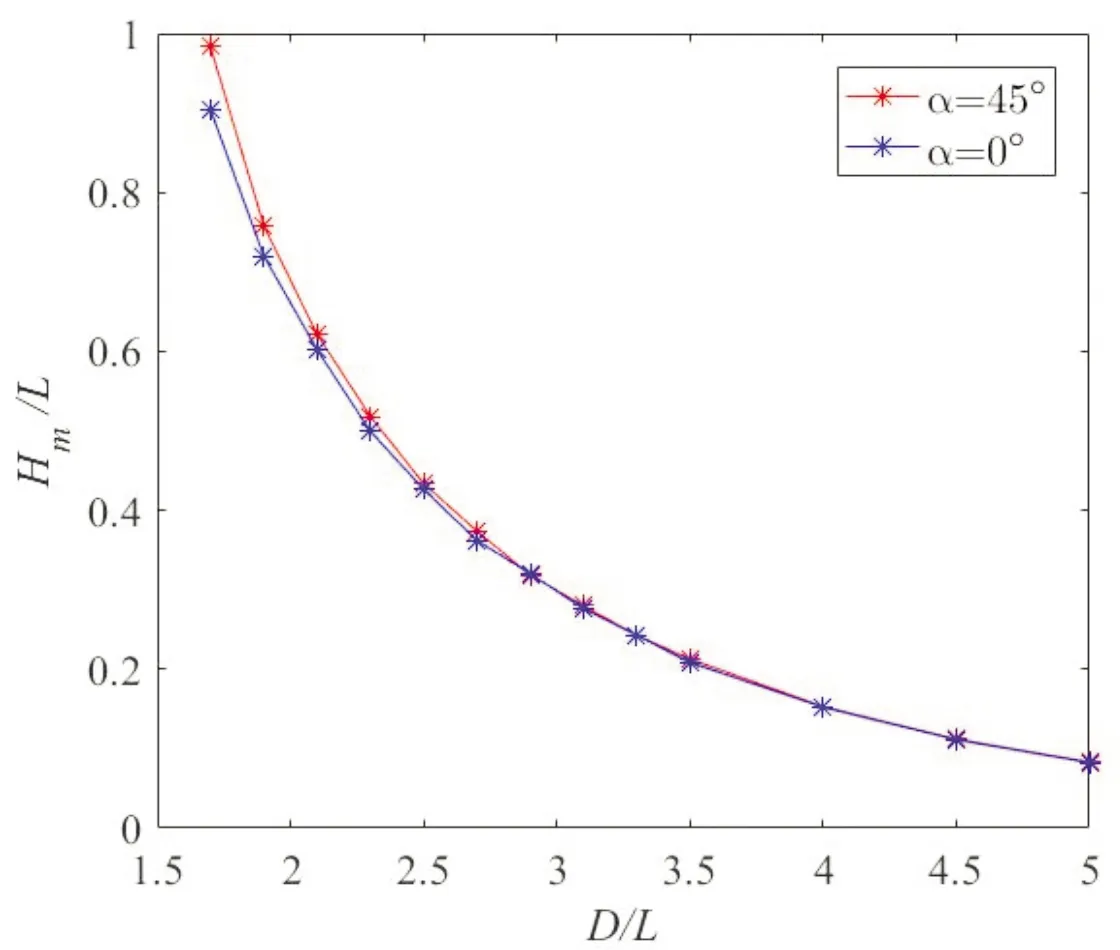
图3 当θ=30°，Bo=1时，在α=0°和α=45° 两种条件下的Hm随D的变化

毛细相互作用与接触角有关。为了显示方柱之间弯月面高度与接触角的关系，图4给出了Hm随θ的变化情况，结果表明：随着接触角的变大，中心高度逐渐变低；当方柱壁面为亲水性时，中心高度高于无穷远处自由面，当壁面接触角为90°时，中心高度等于无穷远处自由面，当壁面为疏水性时，中心高度低于无穷远处自由面。方柱之间弯月面的形状主要是由表面张力与重力平衡决定的。因此，重力也将决定自由面上升高度。

图5以亲水性方柱表面(θ=30°)为例，表示了中心高度随着邦德数(Bo)的变化情况，结果表明：小的邦德数导致了高的自由面中心高度，在接近微重力条件下这种高度增加效果更明显。可以看出，在方柱表面亲水且接触角没有改变的情况下，邦德数越小，自由面能被拉升到更高的位置，在重力加速度极小的情况下，自由面将被拉升到非常高的位置。

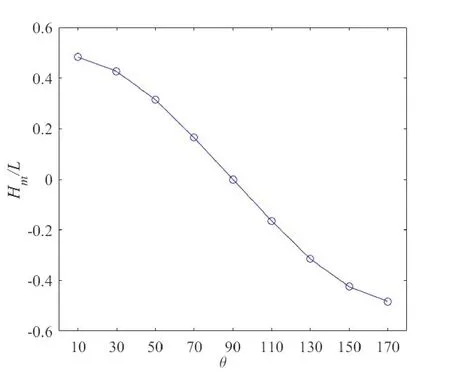
图4 当α=0°，D=2.5 L，Bo=1时Hm随θ的变化

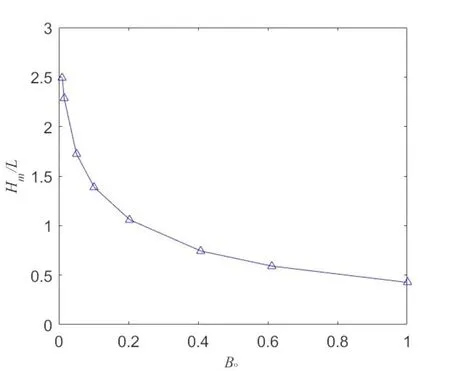
图5 当θ=30°，α=0°，D=2.5 L时Hm随Bo的变化

3 结论

采用最小能量法，对表面张力和重力作用下两方柱间液气交界面形状进行了数值计算，研究了两种放置情况下两方柱间液气交界面形状随着间距、邦德数和接触角条件的变化情况，结果表明：随着表面亲水的方柱间距逐渐减小，方柱间液气交界面逐渐升高，两方柱交错放置比平行放置的液气交界面中心高度更大；表面亲水的方柱平行放置，在间距不变的情况下液气交界面随着邦德数的减小而逐渐升高；平行放置的方柱无论亲水疏水，在间距和邦德数不变的情况下，方柱间液气交界面随着接触角减小逐渐升高。