基于FLUENT的地铁屏蔽门通风数值模拟研究

陈荟多，周东一*

(1.邵阳学院机械与能源工程学院，湖南 邵阳 422000；2.邵阳学院高效动力系统智能制造湖南省重点实验室，湖南 邵阳 422000)

地铁列车运行时，隧道内由于受列车运行活塞效应的影响，会产生大量气流。过大的活塞风会对隧道内设备以及列车上的乘客产生不利影响，这是现代城市轨道交通运营中不可忽视的问题。应用地铁环控系统可有效解决上述问题。屏蔽门系统是地铁环控系统的重要组成部分，因此对地铁屏蔽门通风进行研究具有重要意义。

当前，国内外学者主要针对地铁环控系统及节能优化展开了研究[1-3]。赵西平等人基于西安地铁站台屏蔽门测试了地铁隧道内风速及温度变化，提出了调控通风量的变频技术策略[4]；袁中原等人对复合式屏蔽门系统通风展开研究，提出了两种通风方案并进行了仿真分析，得到了“进站端活塞风井通风模式”优于“出站端活塞风井通风模式”的结论[5]。上述研究都没有针对列车停站时的工况进行相应分析。

综合上述文献分析，笔者首先建立一个前方列车在站内停车、屏蔽门开启且后方列车在隧道内行驶的仿真模型；然后进行相应的计算网格划分，确定好边界条件；最后利用FLUENT进行流场仿真并对屏蔽门系统仿真时的通风进行研究分析，为进一步开展在实际工况下地铁屏蔽门通风的研究奠定基础。

1 模型建立及理论基础

1.1 模型建立

为对地铁运营时地铁屏蔽门系统通风量变化进行研究,建立了一个前方列车在站内停车、屏蔽门开启且后方列车在隧道匀速行驶的仿真模型。考虑到三维仿真方法建模复杂且对计算机要求较高，在保证数值模拟准确性的基础上采用二维仿真模型进行仿真，所建仿真模型如图1所示。

图1 仿真模型示意图

1.2 理论方程

流场数值模拟中控制方程为流场流体的数学表达，笔者所建模型的控制方程表达如下。

连续性方程

式中：ρ为密度，t为时间，u为速度矢量。

能量方程

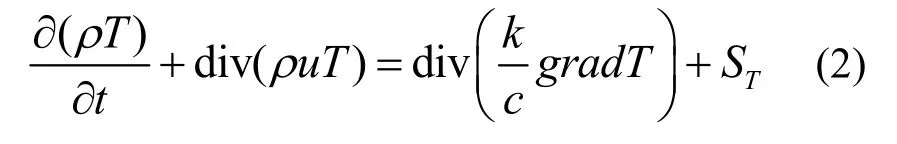
式中：T为温度，c为比热容，k为导热系数。

动量方程：

式中：μ为动力粘度，S为广义源项，θ为速度变量。

2 数值模拟及结果分析

为了对地铁屏蔽门系统开门状态下的通风状况进行研究[6-7]，采用FLUNET对所建模型进行流场仿真。

2.1 计算网格划分

在流体力学计算中，计算网格的划分对流场计算有着至关重要的影响。合理划分出高质量的网格可以使得CFD计算更加准确。考虑到地铁隧道模型建模复杂且模型内部存在动边界问题，笔者基于ICEM的非结构网格对模型进行网格划分，所划分网格最小尺寸为500mm。划分后的计算网格模型如图2所示。

图2 计算网格模型

2.2 边界条件及求解器设置

将ICEM中划分好的网格模型导入到FLUENT中。为了实现仿真模型中列车行驶工况，采用动网格来实现列车与隧道之间的相对运动。在FLUENT仿真中进行任意仿真都需设置好边界条件，边界条件的设置对求解结果的准确性有较大的影响。将所建地铁屏蔽门通风模型边界条件设置如下：

(1)隧道出入口分别为压力入流、压力出流，且存在一定压力差。

(2)井和屏蔽门处为压力出流，压力设置与大气压一致。

(3)其余部分均设置为静止壁面。

2.3 仿真结果分析

各项参数设置完成后，开始进行仿真。考虑到计算精度与计算时长，设置时间步长为0.01s，计算500步长，总计算时间为5.0s。仿真结束时，仿真模型车站处速度云图如图3所示。

图3 停站列车处速度云图

由图3可以看出，仿真结束时，隧道内气流进入车站内时分别沿着停站列车向两端隧道间隙流入；由于车站站厅与车站隧道存在压力差且车站隧道内气压高于站厅气压，因此，靠站厅测气流速度更大，部分气流通过屏蔽门流入站厅，仿真模型中车站屏蔽门处存在速度极小区域。

针对车站屏蔽门整体[8-10]进行分析研究。通过CFD-POST将所研究车站的屏蔽门系统中每一扇屏蔽门处的气流速度变化图分别提取出，并求得其通风量。仿真模型中站台屏蔽门处速度变化如图4所示，各屏蔽门的通风量如图5所示。

图4 站台屏蔽门处速度变化图

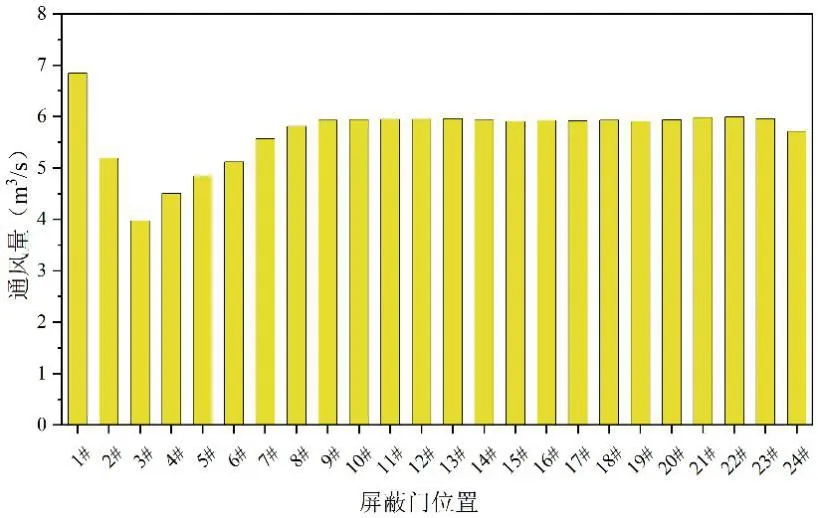
图5 各屏蔽门通风量

由图4可以看出，在仿真过程中，1号至7号屏蔽门处的风速变化较大，8号至24号屏蔽门处的风速变化相对平稳。由图5可看出，各屏蔽门的通风量变化总体呈现先下降再上升最后趋于稳定的趋势，其中1号至7号屏蔽门的通风量变化相对较大。1号屏蔽门的通风量最大，为6.85m3/s；随着通风量的逐渐降低，最低值出现在3号屏蔽门处，为3.97m3/s；4号至7号屏蔽门的通风量逐渐上升；从8号屏蔽门开始，通风量趋于稳定。

3 结论

为对地铁屏蔽门通风进行研究，笔者建立了一个前方列车在站内停车、屏蔽门开启且后方列车在隧道匀速行驶的仿真模型，进行了数值仿真，并对仿真时同一站台各屏蔽门的通风量变化进行了研究。研究结果表明，各屏蔽门的通风量变化总体呈现先下降再上升最后趋于稳定的趋势，其中1号屏蔽门的通风量最大，3号屏蔽门的通风量最小。