一个圆柱形双栅场效应晶体管的物理模型*

刘佳文 姚若河 刘玉荣 耿魁伟

(华南理工大学电子与信息学院, 广州 510641)

1 引 言

目前, 金属氧化物半导体场效应晶体管(metaloxide-semiconductor field-effect transistor, MOSFET)的尺寸从微米级进入纳米级, 为了提高沟道的可控性, 通过在围栅MOSFET器件引入内部控制栅形成的圆柱形双栅(cylindrical surrounding double-gate, CSDG) MOSFET结构, 得到了广泛的关注.与双栅[1]、三栅[2]及围栅MOSFET[3]器件相比, CSDG MOSFET提供了更好的栅控性能和输出特性[4-9].

Fahad和Hussain[10]表明CSDG MOSFET能够在产生更大的驱动电流同时拥有高的面积效率,并实现硅纳米线场效应晶体管所需的低泄漏电流(18.5 nA)特性.Verma等[11]仿真对比了CSDG和圆柱形单栅(cylindrical surrounding gate, CSG)MOSFET的器件特性, 结果表明CSDG MOSFET比CSG MOSFET有更好的漏源电流、跨导等特性.Bairagya等[12]利用Pao-Sah二重积分方法建立了CSDG MOSFET器件的电流解析模型, 得出CSDG MOSFET比传统的单栅MOSFET器件的反型层电荷浓度更高, 具有更好的栅控性能和更大的输出电流.Maduagwu等[13]研究了器件的硅体厚度、栅氧化层厚度和沟道长度等对CSDG MOSFET的阈值电压和亚阈值摆幅的影响, 表明阈值电压随沟道长度的减小而减小, 亚阈值摆幅随硅体厚度、栅氧化层厚度的减小而减小, 随沟道长度的减小而增大.

本文通过求解圆柱坐标系下的二维泊松方程,建立CSDG MOSFET的电势模型, 并由Pao-Sah积分, 建立CSDG MOSFET的漏源电流模型, 进一步分析讨论CSDG MOSFET器件的表面势、表面电场、漏源电流、跨导和阈值电压等特性.

2 物理模型

图1为CSDG MOSFET沿沟道方向的剖面示意图, 图2为CSDG MOSFET圆形横截面示意图.当不考虑CSDG MOSFET的内栅时, 它实际上就是一个围栅场效应晶体管.给外栅加上偏置电压时, 沿着环绕栅的界面生成二维载流子剖面.从俯视图来看, 外栅可以近似为4个有效栅, 产生4个不同的载流子剖面.这些载流子剖面相互作用,导致它们偏离Si/SiO2界面, 向硅体中心移动, 这种相互作用转化为向MOSFET中心的可用载流子态密度的激增.因此, 给围栅场效应晶体管增加内栅形成CSDG MOSFET后, 可以增加载流子剖面相互作用的影响, 使得态密度(以及载流子浓度)的峰值像抛物线一样位于内外栅的中心, 这种现象称为体积反型(volume inversion)[14,15].体积反型使低能带相互作用, 从而提高它们的能级, 处于低能态的少数载流子能够与表面电荷一起参与电流传导.随着晶体管厚度的减小, 由于与氧化物/界面陷阱电荷和表面粗糙度相关的散射减少, 载流子的迁移率增大, 使CSDG MOSFET的输出驱动电流增强, 泄漏电流减小, 短沟道效应减弱.

图1 CSDG MOSFET沿沟道方向的剖面示意图Fig.1.Schematic view of CSDG MOSFET along the channel direction.

图2 CSDG MOSFET圆形横截面示意图Fig.2.Circular cross-sectional view of CSDG MOSFET.

CSDG MOSFET有两种不同的工作模式, 即分离反型和体积反型.在分离反型中, 形成了两个导电沟道, 一个位于外栅氧化硅衬底的界面, 另一个位于内栅氧化硅衬底的界面.在体积反型中, 内外沟道融合到整个硅区.因此, 在这种工作模式下,载流子数量和迁移率都得到了提高, 器件性能也得到了显著提升.

2.1 电势模型

如图3所示, CSDG MOSFET在圆柱坐标系下的二维泊松方程[16]为

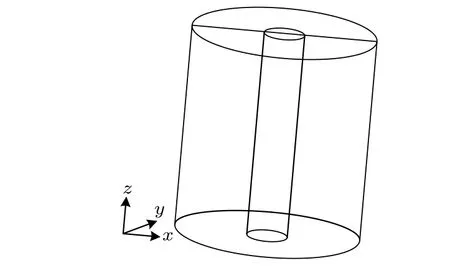
图3 圆柱坐标系下的CSDG MOSFETFig.3.CSDG MOSFET in cylindrical coordinates.

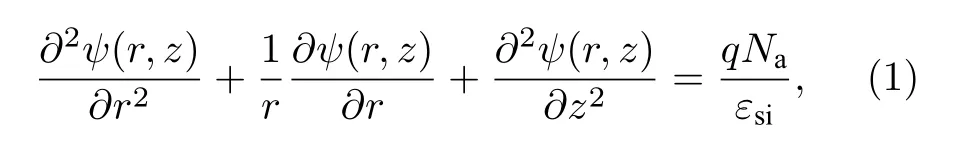
其中, q为电子电量, Na表示沟道掺杂浓度, εsi表示硅的介电常数, ψ (r,z) 为硅薄膜中的电势分布.

由叠加原理, 将电势 ψ (r,z) 分解为1个一维泊松方程的解 V1D(r) 和1个二维拉普拉斯方程的解U(r,z)之和[17]:

V1D(r)满足一维泊松方程[18]:

U(r,z)满足二维拉普拉斯方程[19]:

满足一维泊松方程和二维拉普拉斯方程的解的边界条件如下:

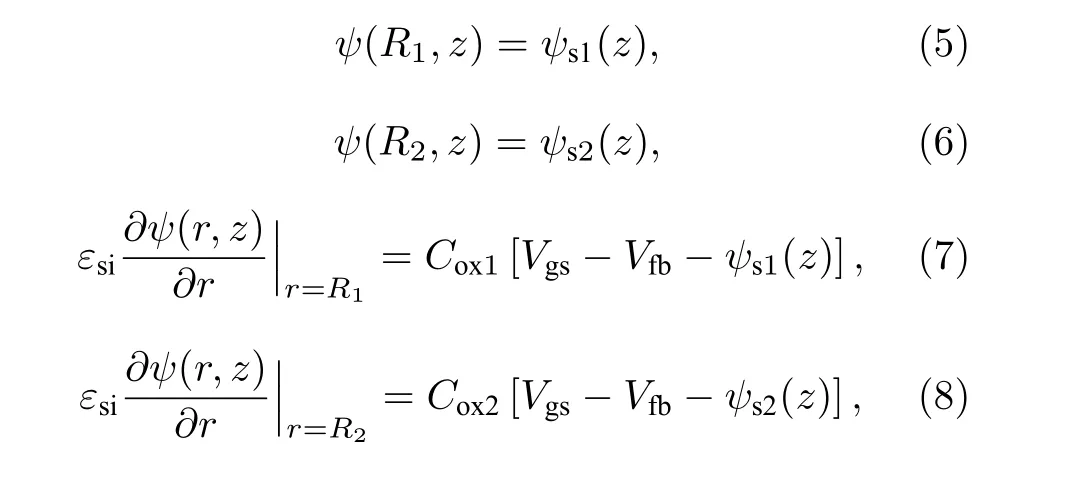
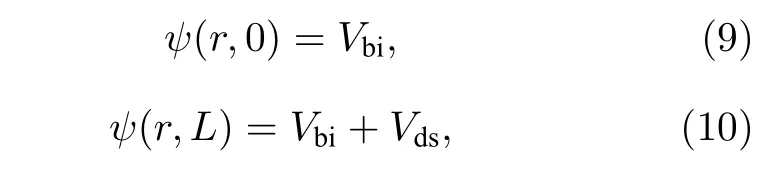
式中, R1表示内栅介质层与硅体接触处半径;R2表示外栅介质层与硅体接触处半径; ψs1(z) 表示内栅 表面势; ψs2(z) 表示 外 栅表 面 势; Vgs表示 栅源电压; Vfb表示平带电压; Vbi表示内建电压; Vds表示漏源电压; L为沟道长度; Cox1和 Cox2为CSDG MOSFET内栅和外栅电容,

其 中, εox表示 栅 介质 层 介 电 常 数, tox表 示 栅 介 质层厚度.

根据边界条件, 求解一维泊松方程和二维拉普拉斯方程, 可以得到 ψ (r,z) 的表达式为[13]

式 中, Csi=εsi/tsi; Cox是栅电 容; An和 Bn是 贝塞尔-傅里叶级数系数; λn是特征值, 满足特征值方程:

其中, tsi为沟道厚度, J0表示零阶贝塞尔函数,J1表示一阶贝塞尔函数.

由于(13)式无穷级数求和中的高阶项快速衰减, 因此CSDG MOSFET内栅和外栅表面势的近似表达式(取n = 0)为[20]

特征值 λ0和系数 A0,B0分别为

CSDG MOSFET沿沟道以及沿半径的电场表达式可以分别表示为

2.2 漏源电流模型

CSDG MOSFET源漏端的表面电势分别为ψs(0) , ψs(L) , 硅体区域的反型电荷可以表示为

其中, i = 1, 2分别表示内栅和外栅.

根据Pao-Sah二重积分, 漏源电流可以表示为[21,22]

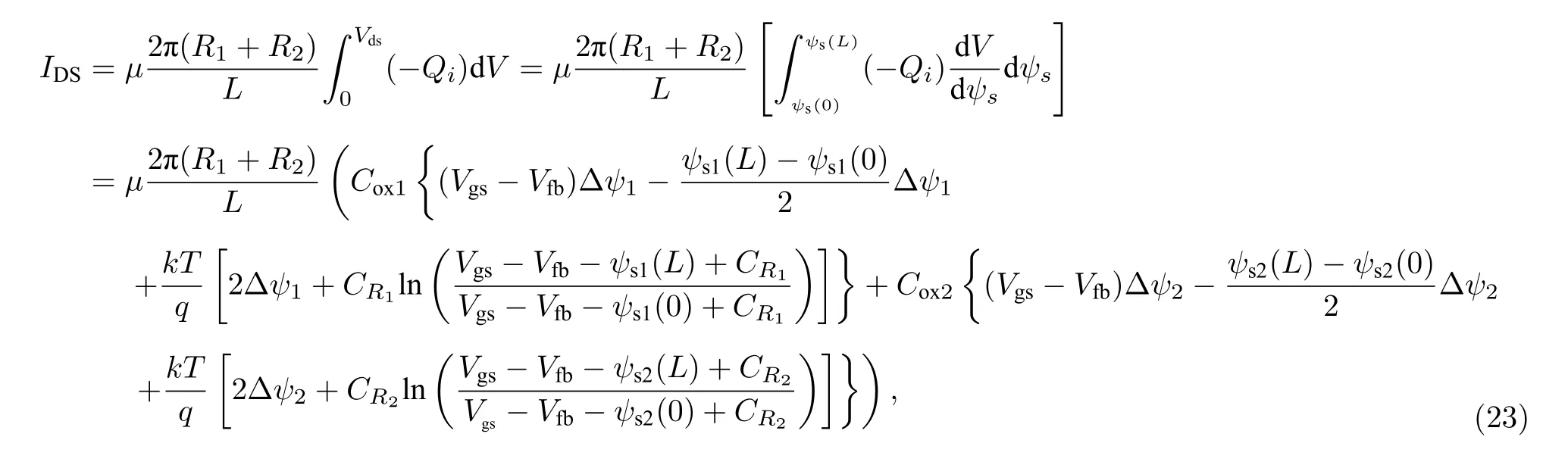
其中, μ 表示沟道载流子迁移率, k表示玻尔兹曼常数, T表示热力学温度.

3 模型仿真与分析

基于上面给出的器件模型, 对CSDG MOSFET特性进行了数值仿真分析, 具体采用的器件参数见表1.其中 ε0为真空栅介质, 3.9ε0为SiO2介质,7ε0为Si3N4介质, 1 2ε0为ZnO介质, 2 0ε0为HfO2介质.

表1 CSDG MOSFET器件参数值Table 1.Model parameters of CSDG MOSFET.

基于(15)式和(16)式的电势模型, CSDG MOSFET在不同栅介质下的外栅表面势沿沟道变化情况如图4所示.由图4可见, 表面势沿沟道先减小后逐渐增大, 最小表面势随栅介质层介电常数的增加而降低, 这是因为栅电容增大后, 垂直电场增大, 栅极对沟道的控制增强, 使沟道表面势下降.

图4 表面势沿沟道的分布Fig.4.Surface potential distribution along the channel.

图5所示为CSDG MOSFET在不同SiO2栅介质厚度下外栅表面势沿沟道变化曲线, 可以看出, 随着SiO2氧化层变薄, 栅极对沟道的控制增强, 垂直电场增大, 使最小表面势下降.CSDG MOS FET在不同沟道长度下的表面势沿沟道变化情况如图6所示, 其中沟道长度为30和50 nm时的电势分布情况与文献[23]的结果基本一致.随着沟道长度的减小, 最小表面势上升, 这是因为沟道长度减小后电荷控制的线性区域减小, 使电势向源区偏移, 从而影响了沟道中心的最小表面势[24].

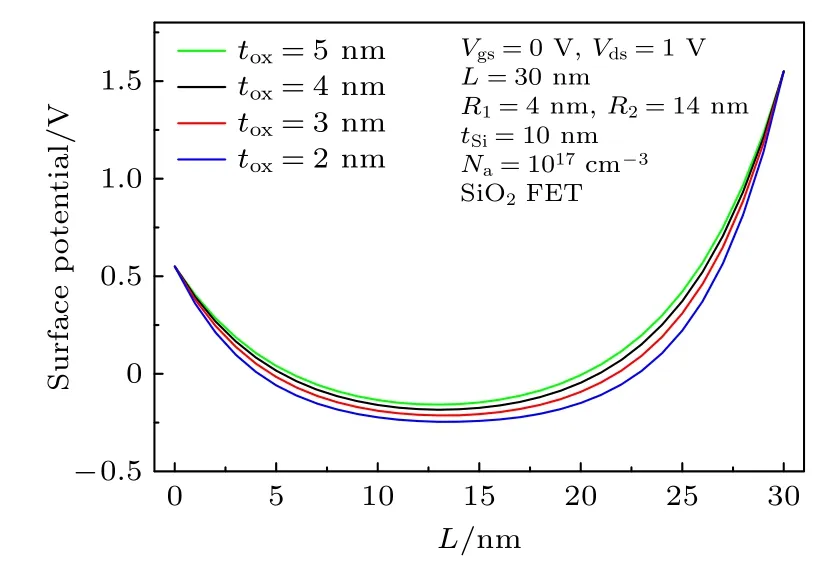
图5 不同氧化层厚度下表面势分布Fig.5.Surface potential distribution with different oxide thickness.

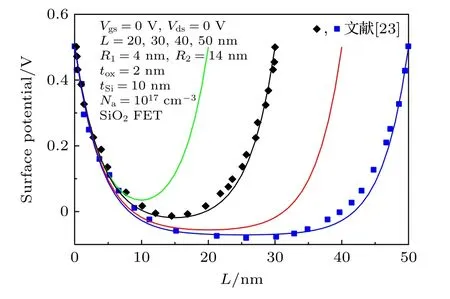
图6 不同沟道长度下表面势的分布Fig.6.Surface potential distribution with different channel length.

CSDG MOSFET在不同栅介质下的电场沿沟道的变化情况如图7所示.随着栅介质层介电常数增大, CSDG MOSFET在源漏端的电场逐渐增大,这是因为栅介电常数的提高使栅电容增大后, 栅极对沟道的控制增强, 源漏端的电场逐渐增大.

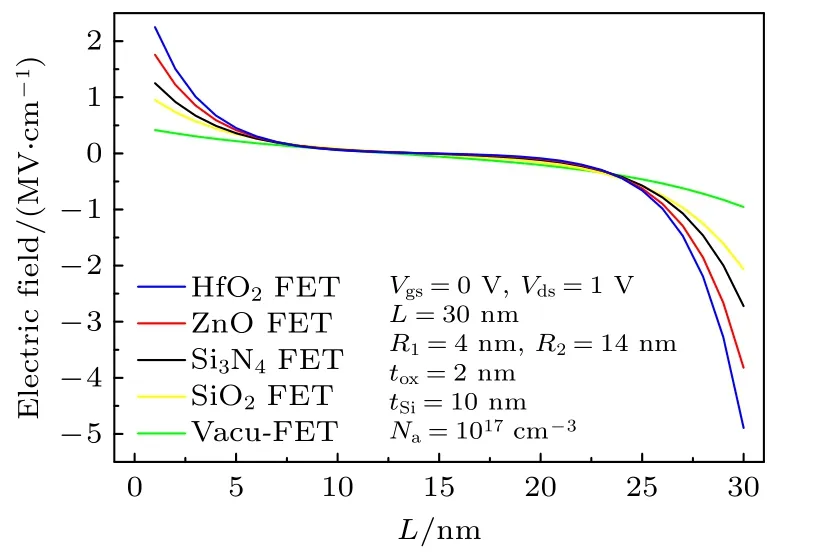
图7 不同栅介质下外栅表面电场沿沟道的分布Fig.7.Electric field distribution along the channel at the outer surface of CSDG MOSFET with different gate dielectric.

在漏源电压固定时, SiO2介质下CSDG MOS FET在不同栅源电压下的电势和电场沿半径变化情况如图8和图9所示, 随着栅源电压增大, 电势逐渐增大且变得更平缓, 电场减小.

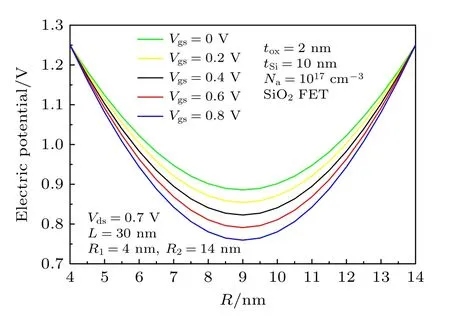
图8 不同栅电压下电势沿半径的分布Fig.8.Electric potential distribution along the radius with different gate voltage.

图9 不同栅电压下电场沿半径的分布Fig.9.Electric field distribution along the radius with different gate voltage.

CSDG MOSFET在不同栅介质下的电场沿半径变化情况如图10所示, 真空栅介质时CSDG MOSFET的电场较低, 随着栅介质层介电常数的增大, 栅极对沟道的控制增强, 沿半径的电场也逐渐增大.

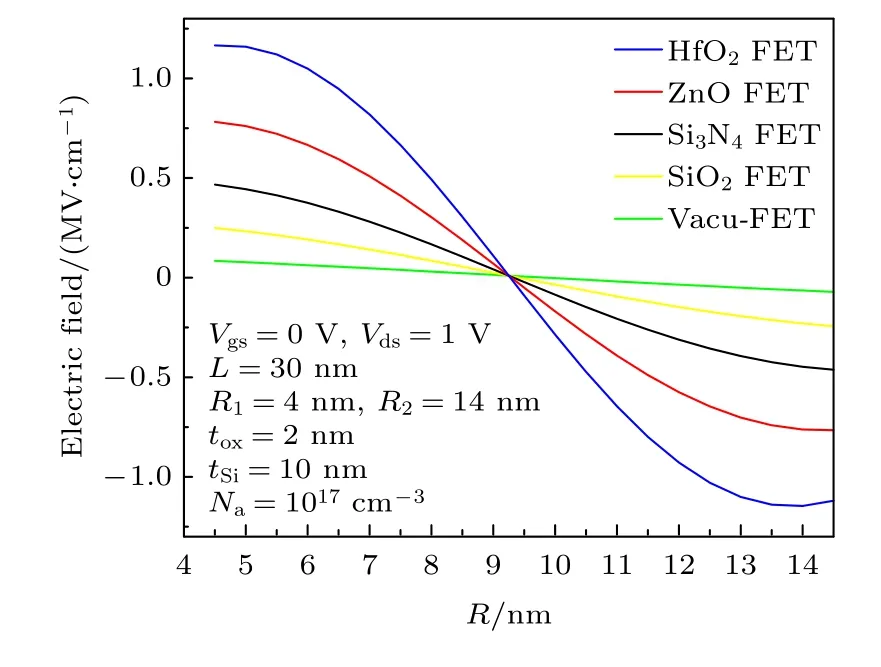
图10 不同栅介质下电场沿半径的分布Fig.10.Electric field distribution along the radius with different gate dielectric.

图11是CSDG MOSFET在不同栅介质下的漏源电流随栅源电压变化曲线, 插图为不同栅介质下的阈值电压对比.由图中 Ids— Vgs变化关系可知,当 Vgs达到一定值后, 电流开始迅速增加, 说明CSDG MOSFET的栅控性能得到了较大程度的提高.若以漏源电流2.0 × 10—7A时的栅源电压作为阈值电压[25], 由图11可见, 随着栅介质常数的增大, 栅控性能变好, 沟道反型电荷密度增大, 漏源电流增加, 阈值电压逐渐减小.

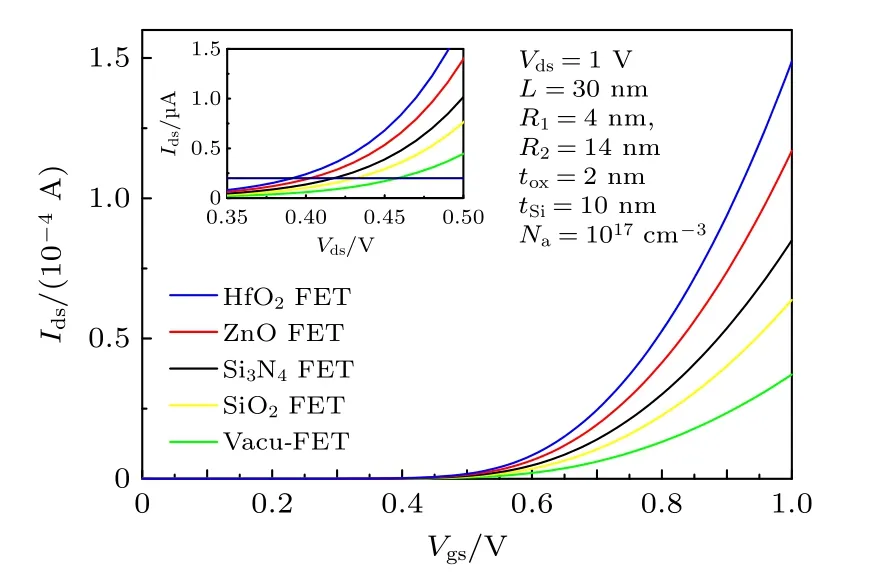
图11 不同栅介质下 I ds - V gs 曲线Fig.11.Curves of I ds versus V ds with different gate dielectric.

图12 是CSDG MOSFET在不同SiO2栅介质厚度下的跨导随栅源电压变化曲线.跨导随栅介质厚度的增大而减小, 这是因为栅介质厚度增大后栅电容减小, 垂直电场减小, 栅极对沟道的控制减弱, 使CSDG MOSFET的漏源电流减小, 跨导减小.

图12 不同SiO2栅介质厚度下的跨导Fig.12.Transconductance with different SiO2 dielectric thickness.

为了对基于(23)式的漏源电流模型的仿真结果与TCAD的仿真结果进行比较, 用文献[26]中给出的器件尺寸和材料参数进行仿真, 结果见图13,模型仿真得到的 Ids- Vds特性与TCAD的结果[26]基本一致.

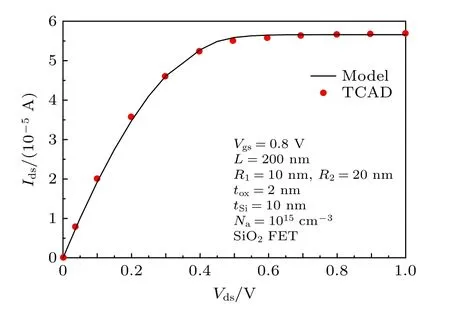
图13 本文模型仿真得到的 I ds - V ds 曲线与TCAD结果比较Fig.13.Curve of I ds versus V ds between the model in this paper and the TCAD result.

为了探讨10 nm下CSDG MOSFET的特性,进一步根据上述的仿真结果, 按比例缩小CSDG MOSFET, 具体参数见表2.图14和15分别是根据表2参数仿真得到的CSDG MOSFET输出特性和跨导特性.在栅长为3, 5, 7, 10 nm下, CSDG MOSFET的漏源电流和跨导随栅长的减小而减小, 这是由于随着栅长、半径的等比例减小, 沟道最小表面势上升, 反型电荷密度减小, CSDG MOSFET的漏源电流减小; 栅极对沟道的控制减弱, 导致跨导减小.

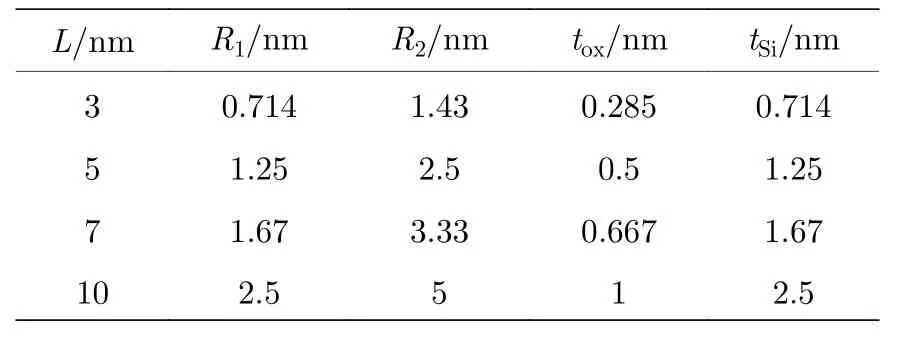
表2 不同栅长的CSDG MOSFET器件参数值Table 2.Model parameters of CSDG MOSFET with different gate length.

图14 不同栅长下的输出特性Fig.14.Curves of I ds versus V ds with different gate length.

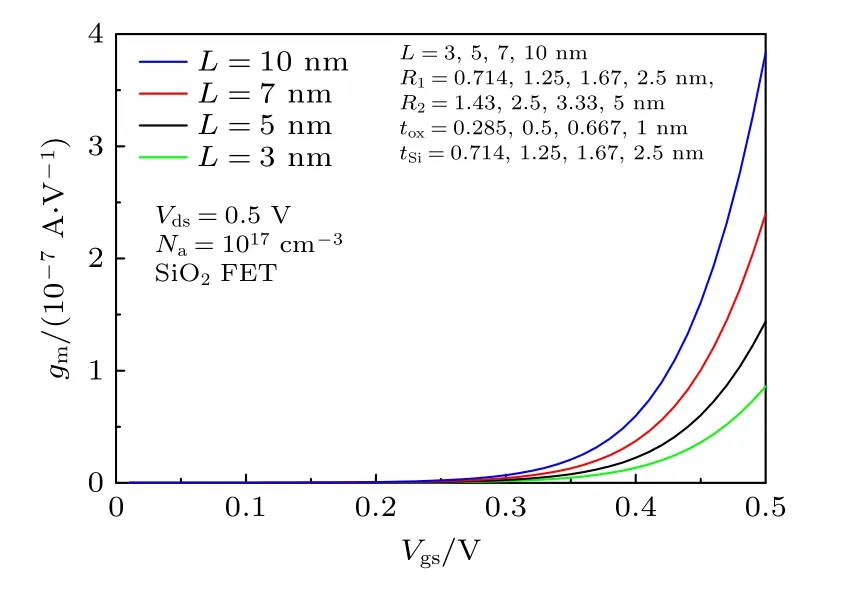
图15 不同栅长下的跨导Fig.15.Transconductance with different gate length.

4 结 论

本文通过求解圆柱坐标系下的二维泊松方程,得到了CSDG MOSFET的电势模型, 通过对反型电荷沿沟道积分, 得到漏源电流模型, 分析讨论CSDG MOSFET器件的特性.结果表明: 相同Vds下CSDG MOSFET的最小表面势随栅介质常数增大而减小, 随沟道长度减小而增大, 随栅介质厚度减小而减小; CSDG MOSFET沿沟道与沿半径方向的电场、漏源电流随栅介质常数的增大而增大; CSDG MOSFET沿半径方向的电势随栅源电压的增大而增大; CSDG MOSFET的阈值电压随栅介质常数的增大而减小; CSDG MOSFET的跨导随栅介质厚度的增大而减小.随着器件参数的等比例缩小, 沟道反型电荷密度减小, 其漏源电流和跨导也减小.