基于自适应匹配追踪算法的齿轮箱轴承故障特征提取

李有新

(青海高等职业技术学院 机电工程系，青海 海东 810799)

0 引言

由于齿轮箱故障振动信号稀疏、效果差，包含大量的噪声，所以对齿轮箱故障诊断在于如何剔除噪声信号和有效提取齿轮箱故障信号特征[1-3]。近年来很多学者针对齿轮箱的故障诊断开展研究。杨秀杰等人提出的匹配追踪在齿轮故障诊断中的应用，成功提取了故障齿轮的冲击信号[4]；王平等人发表了匹配追踪算法的优化及其在滚动轴承故障诊断中的应用，进而对匹配追踪算法进行优化，更好地剔除噪声信号[5]。匹配追踪算法每次迭代的结果是次最优的，这导致重构的信号精度不够，需要的内存大，运行时间长，效率低[6]。基于此，王聪等人提出齿轮箱故障诊断中的自适应匹配追踪算法[7]，该方法通过定量提取故障特征，将已知故障信号分类特征与实验信号特征进行对比，成功提取齿轮箱故障特征，并对故障类型进行分类。SAMP算法需要多次去选择信号的稀疏度，而稀疏度的选取直接影响算法重构信号的精度，且SAMP算法迭代过程中每次只选择一个原子来更新子集合，这都导致重构时间过长，而且每次重构时恢复数据的计算存在误差[8-10]。为了提高齿轮箱轴承内外圈在传动振动过程中故障诊断能力，采用自适应匹配追踪(SAMP)算法建立了故障诊断模型，并展开了仿真分析及实验验证。

1 自适应匹配追踪算法

1.1 自适应匹配追踪算法

本文主要采用SAMP算法提取齿轮的故障特征。SAMP算法是在自适应匹配追踪算法基础上加入步长和支撑集的概念[11-12]，可以在未知信号稀释度的情况下，应用回溯思想，经过预先、候选以及剪裁三步，分段进行。在每一段都采用逐步更新步长、不断增大支撑集、增加原子规模逐步逼近稀疏度的方法，直至达到迭代条件，退出迭代，来更加精确地重构故障信号。自适应匹配追踪算法能够有效降低齿轮箱振动故障信号中的噪声，同时减少了重构的时间。对于稀疏性差的信号也能有相对好的处理效果。基本原理如图1所示。

图1 SAMP算法基本原理图

U=abs[ATrt-1] (即计算〈rt-1,aj〉，1≤j≤N)

(1)

式中：选择u中L个最大值，将这些值对应A的列序号j构成集合Sk(列序号集合)。

SAMP算法分多阶段迭代，在每个阶段不改变支撑集的大小。

另At={aj}，再求取y=Atθt的最小二乘解：

(2)

(3)

1.2 SAMP算法的有效性验证

为了验证SAMP算法的有效性，本文构造了一个一维随机信号，测量个数M=64，信号长度N=256。分别通过SAMP算法作仿真信号的重构信号与残差图，信号稀疏度与测量精度图。

由图2(本刊黑白印刷，相关疑问咨询作者)的SAMP算法重构图可知，SAMP算法能够精确重构出一维随机仿真信号，能够剔除信号的残差信号，并提出信号的主要特征。

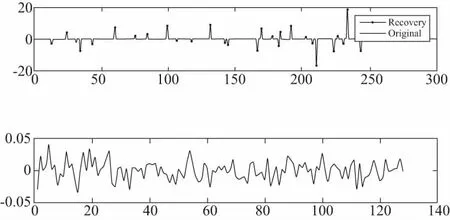
图2 SAMP算法重构图

由于大多数信号不具备稀疏性，需要选取合适的测量矩阵和稀疏矩阵。本文构造了一个N×N的随机高斯测量矩阵，稀疏矩阵选择单位矩阵，运用到SAMP算法能够处理稀疏性差信号，且重构精度高。步长的选取也影响重构的精度，处理齿轮箱故障振动信号时，选择固定步长为5，经过验证能够保证稀疏度估计的准确性。本文改变以往匹配类追踪算法选择设置迭代步数作为终止条件的方法，把残差值是否达到0作为终止条件，能够更加有效地使噪声值降到最低，更加有效地提取故障的主要特征。

2 仿真分析

2.1 仿真轴承故障信号

在实际工作中，滚动轴承存在微弱振动，不会对正常工作产生影响，当有部分零件出现损伤时，损伤的滚动轴承的零部件会有周期性振动。振动信号的表达式如下：

(4)

式中：M为冲击的个数；Bm为冲击的幅值；β为冲击的衰减系数；Tp为相邻冲击之间的间隔；fc为故障的特征频率(fc=1/Tp)；fre为共振频率。

2.2 轴承的外圈振动信号

为了验证SAMP算法对轴承故障信号的降噪效果，简化轴承的外圈故障信号数学模型，便于分析轴承故障。其表达式如下：

(5)

设轴承固有振动频率为fn=1 000 Hz，位移常数为y0=5，阻尼系数为ζ=0.1，冲击周期为0.01 s，采样频率为fs=4 096 Hz，采样点数N为1 024。加入噪声N(t)为高斯噪声信号。转频fr=12，外圈通过频率为foc=36 Hz。

如图3所示，从SAMP算法重构轴承外圈仿真加噪信号时域波形图中看到，轴承外圈故障仿真加噪信号被淹没在噪声中。对比图2、图3，通过SAMP算法对轴承外圈故障仿真加噪信号处理，不仅能够看到信号呈周期性波动，还能够清楚看到齿轮的故障。从频谱图中能够清楚显示了滚动轴承的固定频率为1000Hz,且固定频率周围出现(1 000±36)Hz的边频带。

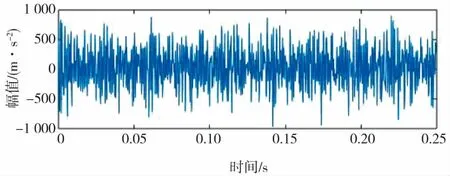
图3 SAMP算法重构轴承外圈仿真加噪信号图

2.3 轴承内圈振动仿真信号

简化轴承的外圈故障信号数学模型，便于分析轴承故障。其表达式如下：

(6)

Bm=cos(2πfrt+ΦA)+y0

(7)

式(6)-式(7)中，设轴承固有振动频率为fn=1 000 Hz，位移常数为y0=5，阻尼系数为ζ=0.1，冲击周期为0.01 s，采样频率为fs=4 096 Hz，采样点数N为1 024。加入噪声N(t)为高斯噪声信号。转频fr=12，内圈通过频率为foc=59 Hz。

从图4时域波形图中看到，轴承内圈故障仿真加噪信号不呈周期性波动。经过SAMP算法处理的轴承内圈故障仿真信号呈周期性波动，能够清楚看到滚动轴承的故障。SAMP算法重构轴承内圈仿真加噪信号频谱图能够清楚显示了滚动轴承的固定频率为500Hz，且固定频率周围出现(500±20)Hz的边频带。在SAMP算法重构轴承内圈仿真加噪信号谱图中显示了轴承内圈通过频率60Hz以及转频10Hz，且出现轴承内圈通过频率的5倍频，在轴承内圈通过频率周围出现(60±10)Hz，且轴承内圈通过频率和倍频以及边频带呈现逐步衰减，故障特征明显。

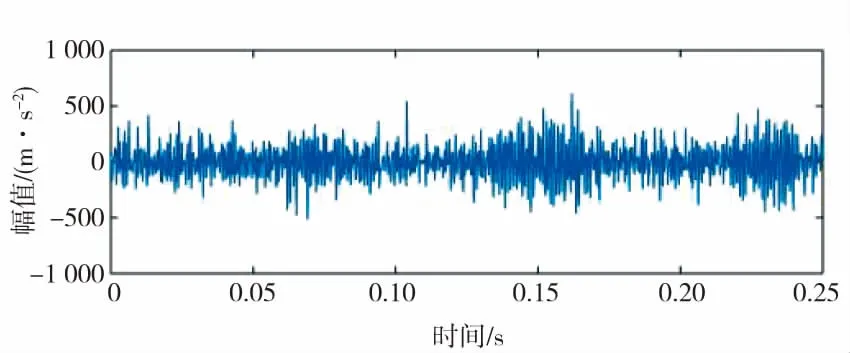
图4 SAMP算法重构轴承内圈仿真加噪信号图

3 结语

1)轴承外圈故障仿真信号呈周期性波动，能够清楚看到滚动轴承外圈的故障，轴承外圈的通过频率及其倍频呈现逐步衰减，轴承外圈故障仿真加噪信号被淹没在噪声中。通过SAMP算法对轴承外圈故障仿真加噪信号处理，能够看到信号呈周期性波动。

2)轴承内圈的通过频率和倍频以及边频带呈现逐步衰减，故障特征明显。从SAMP算法重构轴承内圈仿真加噪信号时域波形图中看到，轴承内圈故障仿真加噪信号不呈周期性波动。经过SAMP算法处理的轴承内圈故障仿真信号呈周期性波动。