基于增益-调度控制和高保真飞机模型的实时四维航迹生成

Olusyo Ojemu , Mhdi Mhfouf , Lohithksh M. Miyr , Arr Al-Hindi ,Mihl Weiszer , Jun Chen ,*

© 2021 THE AUTHORS. Published by Elsevier LTD on behalf of Chinese Academy of Engineering and Higher Education Press Limited Company This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

1. 引言

近来的研究表明，为了实现高效运作，满足机场不断增加的飞机和客流量的需求，有必要对每架航班实施门到门的全程引导[1,2]。这种全程引导被称为四维航迹（4DT）引导。四维航迹是指飞机从登机口到跑道的时空导航（包括滑行和回推路径）[3]。四维航迹引导系统不仅能优化地面运动的各个阶段，而且还能协调机队的行动。四维航迹引导系统能减少高达55%的滑行延误[4]。因此，许多空中交通管理人员目前正在研究如何提高机场的数字化水平，包括新的地面决策支持和导航技术，以应对拥堵并提高机场运行的鲁棒性[1]。到2035年，乘客数量将增至2012年公布数量的1.5倍[1,5]，为了完成管理各个机场的飞机地面运动这一日益艰巨的任务，实现四维航迹算法变得更加紧迫。此外，飞机排放占全球温室气体排放的3% [5,6]，这为地面运动优化提供了重要动力。

人们针对机场地面决策支持和导航系统的可行性进行了大量的研究[7-10]。这些研究大致可以分为两类。第一类包括优化机场地面作业的路径和调度的算法。这类研究更关注整个机场的运行模式，而不是特定的飞机。这类算法主要解决的是滑行时间的最小化问题[4,11]，并不主动或直接优化燃油效率及其排放。少数例外情况，如主动路径和调度算法，直接考虑燃油消耗和排放[5,12]。然而，这些算法以简化的飞机运动方程和燃料排放模型为基础，生成的四维航迹可能不符合操作限制，而且由于其与预设的四维航迹不完全一致，遵循这些轨迹可能会增加燃料的消耗和排放。另外，考虑计算的复杂性，用来生成四维航迹的算法通常是离线执行的[5,9]，因此很难在出现全新事件时自动生成新的轨迹。

第二类研究与控制算法有关，这些算法针对特定的飞机，可以实现预定的输出以及研究人为因素的影响。Haus等[7]研究了自动化系统如何帮助飞行员在滑行过程中进行决策。为了成功生成四维航迹，必须将这两种方法紧密结合起来进行使用。具体来说，调度程序会根据某种最优调度方法来确定最优时限和路径点[11]，而特定的飞机则以最优方式遵循该最优调度。

通常情况下，飞机能够如实地遵循既定调度，这需要由飞行员来控制环路。有时，调度程序会给出一个最优速度轨迹（如参考文献[5,13]），但要求飞行员严格遵循速度轨迹是不现实的，因为飞行员在滑行过程中的工作量非常大，而且在滑行操作中经常要执行一系列复杂的项目检查工作。为了解决上述问题，研究人员开展了在滑行中使用全自动系统的研究[8]。然而，由于在地面作业中采用自动滑行系统仍具有很多问题，全自动滑行模式没有得到广泛应用[8]。但是，正如下一代航空运输系统（NextGen）[2]和欧洲单一天空空中交通管理研究（Single European Sky Air Traffic Management Research, SESAR）报告[1]中讨论的那样，为了满足严格的四维航迹要求，就必须引入全自动滑行系统。采用半自动滑行模式可以规避这一问题。例如，参考文献[8]主要研究了以人为中心的四维（4D）地面导航系统，其中飞行员仍负责控制飞行，信息通过滑道照明元件被传递给飞行员，以帮助其决策。这种方法被称为followthe-greens方法[14]，目前伦敦希思罗机场和新加坡樟宜机场等全球各大机场都在使用该方法[7]。然而，这种半自动滑行模式存在一些缺陷。第一，由于没有采用全自动滑行，这种模式并不能完全跟随所要求的四维航迹。此外，此类系统在设计最优控制系统时，通常会做出许多与实际情况不符的假设，如飞行员以怠速滑行。参考文献[15]指出，滑行过程中的功率设置并不是固定的，通常取决于飞行员的操作行为。如果飞行员偏离这些假设，就会出现次优滑行。另外，许多引导飞行员滑行的算法并没有主动降低燃料燃烧或发动机的排放。例如，参考文献[7]提出的引导系统确保了轨迹能够被严格遵循，但并未考虑燃料和排放问题。

本文提出了一种新的自动化系统。该系统能够完全实现四维航迹导航，并且主要用于两种情况：①作为反应型决策支持工具，生成能够解决全新事件的新轨迹；②充当半自动和全自动滑行的自动驾驶系统。本文所采用的方法是求解一个离线优化问题，即找到基于比例-积分-微分（PID）的控制系统的增益，使特定目标函数最小化。目标函数一经确定，就能和调度算法紧密结合，并且该方法考虑了高保真飞机模型的燃油消耗和排放。具体而言，该调度算法考虑了基于飞机模型的约束，确定了最优的滑行路线，然后控制飞机的滑行，此过程利用了最优PID增益，使其以最优方式遵循调度。这种方法的优点在于使用了一种直观、简单而高效的比例-积分-微分控制系统。由于控制器的优化在在线部署之前是离线运行的，因此易于部署，且不需要在线优化，减少了在线计算的繁重的工作量。因此，每当有干扰使调度算法的原始计划不可行时，通过该算法可以在线生成一个新的、高效的四维航迹。

就像飞机在飞行模式中的自动驾驶一样，该控制系统能被直接应用在飞行控制装置中。这种方法允许全自动滑行，而不需要飞行员进行干预。此外，该控制系统可以为飞行员提供决策支持，其方式类似于前文的follow-the-greens方法。特别地，该方法可以帮助飞行员确定适当的控制输入组合，以确保目标函数（燃料消耗）在半自动滑行时最小化。参考文献[16]全面回顾了最优控制算法的使用。

本文其余部分的结构如下：第2节提供了利用大型喷气式飞机模型验证该算法的详细过程；第3节对该算法进行了描述并解释了如何将其用于飞机的自动滑行；第4节概述了将该方法应用在复杂飞机模型上的结果；第5节总结全文，概述了所取得的成果，并对未来的研究方向提出建议。

2. 飞机模型建立

本节介绍了研究中使用的非线性波音747-100飞机模型的数学方程。该数学模型是由刚体运动的一般方程导出的状态空间模型公式。根据牛顿力学，对于运动中的刚体，线速度和角速度（分别用V和Ω表示）的变化率与作用在该刚体上的合力和力矩有关，如下式所示：

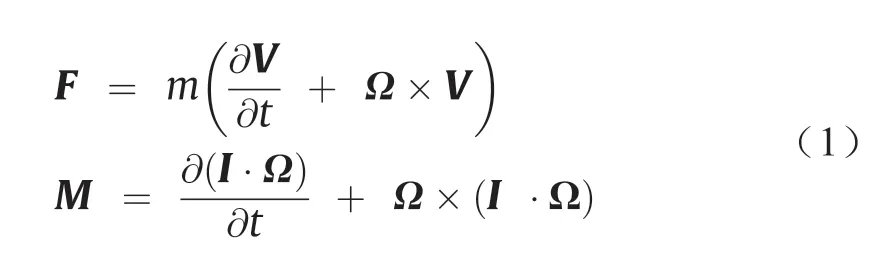
式中，F= [Fx Fy Fz]T和M= [L M N]T分别是沿着机体坐标系中x、y、z轴的力和力矩向量；V=[u v w]T是线速度向量，其中u、v、w分别是x、y、z轴上的速度；Ω= [p q r]T是角速度向量，其中p是滚转角速度，q是俯仰角速度，r是横摆角速度；m是飞机的质量；t是时间；I是恒定惯性张量（飞机的力矩和惯性的乘积）[17]。式（1）可以改写为如下状态空间公式：

式（2）为标准状态空间形式，一般可以写成：

式中，x∈RK是相应时间导数，用x·表示。其中R代表实数；K代表状态的总数。u∈RW代表维度W的时变输入；υ∈RZ是维度Z的扰动向量（如大气扰动）。式（3）是非线性时变状态方程，该方程对飞行器所受的力和力矩进行了隐式建模。

式（3）的非线性时不变等效模型一般能模拟包括飞机在内的任何实际的物理动力系统。因此，本研究假设为非线性时不变模型。尽管惯性矩取决于许多其他因素，如飞机的质量等，但它与时间（即飞机的机龄）无关。在本研究使用的波音747-100飞机模型中，状态变量的个数为13。具体来说，这些状态包括标准的12维变量（控制机身角速率和加速度）以及一个被称为“预推力”（pre-thrust）的附加变量。这些状态用于描述发动机的动态性能。2.2节对状态方程作了简要描述。

2.1. 波音747-100飞机模型

波音747-100是一种四扇喷气式大型运输机，于1967年投入使用。波音747-100配备一个舵柄和一个方向舵，在滑行时便于控制方向。假定推力由两个内部发动机产生。波音747-100还配备了内外克鲁格襟翼和带有四个副翼的可移动稳定器，由于在滑行过程中没有使用它们，因此它们没有被包含在模型中。研究中用于波音747-100建模的数据来源于参考文献[18,19]。

作用在机体坐标系上的力和力矩的设定如图1所示。图2显示了在本研究中用于建模的飞机部件。发动机和燃油系统是根据国际民用航空组织（ICAO）的数据库进行建模的。

2.2. 状态方程

如前文所述，非线性状态方程由13个非线性函数组成。这些状态又细分为以下几个子状态：

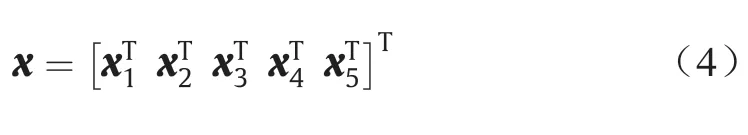
式中，x1、x2、x3、x4、x5分别代表旋转速度、平移速度、姿态、位置和预推力子向量。x1= [p q r]T、x2= [V α β]T、x3= [φ θ ψ]T、x4= [h x y]T、x5=预推力。x1取决于滚转角速度p、俯仰角速度q和横摆角速度r；x2是线速度向量V、迎角α和侧偏角β的函数；姿态向量x3是滚转角φ、俯仰角θ和偏航角ψ的函数；位置向量x4由高度h和位置x、y组成。旋转速度和平移速度分别是在飞机的机体坐标系和气流坐标系内定义的，而姿态和位置是在地面坐标系中定义的。最后一个变量表示推力，在飞机的机体坐标系中也有给出。将向量状态导数与向量状态和输入联系起来的向量函数f如下式所示：

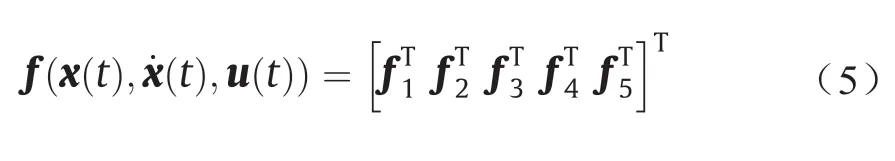
图1. 飞机的力和力矩的设定。

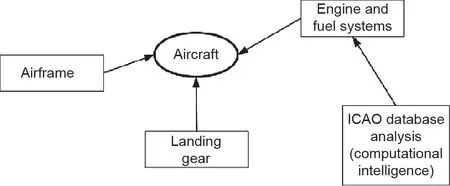
图2. 飞机滑行部件及其设定。ICAO：国际民用航空组织。

式中，f1、f2、f3、f4和f5分别代表旋转、平移、姿态、位置和预推力向量与状态变量之间的向量子函数。除了预推力变量外，每个子函数都源自参考文献[20]，子函数详见附录A。

在波音747-100飞机模型中，发动机增压比（EPR）或预推力决定了飞机产生的推力。这一推力由时间常数为5 s的一阶动态系统表示。为了使其与其他状态方程兼容，并且为了便于模型的建立，需将其转换为状态空间形式。对于给定的静态EPR（即稳态值）[这一数值取决于节流阀调定（thr）]，预推力可由以下公式得到：

式中，g代表静态EPR，是与节流阀调定和给定状态有关的函数。如2.3节所示，已知预推力，可以计算出发动机产生的推力。状态方程适用于任何飞机，但是每一架飞机有不同的力和力矩值。对力和力矩分量以及所使用的数值推导见2.3节。

2.3. 力和力矩的推导

本节给出了波音747-100飞机模型的力和力矩方程，包括气动元件、发动机元件和起落架元件，其数据来自参考文献[18,19]。

2.3.1. 气动力和力矩

当飞机滑行时，特别是在相对高的滑行速度下，气动力和力矩是不可忽略的。力和力矩的气动力分量都是在气流坐标系上计算的，然后被转换到机体坐标系上。气动力数据集以无单位特征系数C*的形式得到。如附录A所示，下标*是指定的6种气动力分量的6个下标之一。

2.3.2. 发动机力和力矩

波音747-100飞机模型有4台Pratt和Whitney JT9D-3发动机，起飞推力为43 500 lbf (193 500 N)。在整个模拟过程中假定只有两台发动机运行。因为滑行过程中通常不使用反向推力[它只在着陆到大约100 kn（51 m·s-1）时使用]，所以飞机发动机的建模过程不考虑反向推力。按以下步骤计算发动机产生的最终推力。

（1）首先得到节流阀角度，然后利用这个角度计算发动机油门杆角度（PLA）。需要注意的是，本文已经对开发的波音747-100飞机模型做了一些修改，以规范节流阀调定系统，使输入系统中的是一个在0和1之间的数字。在波音747-100飞机模型中，介于60°～130°的节流阀角度被转换为0～1的数字。使用以下公式对其进行标准化。

（2）给定发动机油门杆角度（或使thr规范化为0～1，如模型所示），以确定静态EPR。与thr和EPR相关的多项式模型如下式所示：式中，k0、k1、k2、k3是多项式系数，如表1所示。

表1 计算EPR的多项式函数的系数

（3）如前文所述，发动机包括一个瞬态系统，该系统由一个时间常数为5 s的一阶动态系统表示。最后一步计算出的静态EPR表示EPR的参考水平或稳态。值得强调的是，瞬态系统可由状态空间形式表示，因此如前文所述，需要增加一个状态预推力。从本质上讲，预推力变量代表了动态EPR。

（4）根据参考文献[18,19,21]，美国国家航空航天局（NASA）提供了随着飞机马赫数增加，在动态EPR中增加增量EPR的图。然而，本次模型并未考虑EPR的增量[因为滑行速度通常小于40 kn（21 m·s-1），所以速度增加带来的EPR的增量可以忽略不计]。

（5）当EPR已知（EPR本质上是动态的）时，最后一步是计算每个发动机推力的净推力。净推力是与发动机EPR和环境条件有关的函数。净推力的推导公式如下：

式中，斜率为90°，截距为-90°。

由于在所开发的模型中使用国际单位制（SI）进行计算，因此以磅（lb, 1 lb = 0.453592 kg）为单位的推力乘以因子4.44822后被转换为牛顿。上述步骤中推导出的推力仅适用于一台发动机。综上所述，计算每台发动机推力的过程如图3所示。

怠速推力：在节流阀调定为零时，EPR的近似值为1.02，这使得发动机产生正的净推力。同样值得注意的是，发动机会在飞机的重心附近产生力矩。在双引擎滑行模式（使用内引擎，关闭外引擎）中，发动机推力产生的净力矩为零，而在单引擎滑行模式中，发动机将产生一个力矩使飞机偏航。这个力矩由力和发动机离飞机重心的距离的乘积进行计算。根据参考文献[18,19]，这个距离等于39.167 ft（11.938 m）。

图3. 计算净推力的步骤。

燃油流量和排放：由于本研究的目的之一是寻找更有效的方法来帮助飞机滑行，因此准确测量发动机燃油消耗和排放至关重要。基于ICAO燃油和排放数据库[22]，我们建立了一个发动机油耗模型。ICAO数据库已被广泛应用于研究在不同推力设置下的燃油消耗和发动机排放[15]。该数据库提供了1980年以后生产的大约500台发动机的列表，以及它们在4种不同推力设置下的燃料消耗和排放情况。数据库中所有发动机的额定推力分布如图4所示。

图4. ICAO数据库中发动机额定推力的分布。

除参考文献[22]所示的排放和燃料统计数据外，ICAO数据库还包含与发动机有关的其他重要信息，如停产状态、燃料类型、发动机制造商以及发动机是否停用。数据库列表中不包括JT9D-3发动机，可能是由于该发动机是在1980年之前制造的。为了便于计算JT9D-3发动机的燃料燃烧和排放，我们对数据库进行了全面的统计分析。先前，已经有人使用过模糊逻辑模型来分析这类数据[23-25]。研究发现，发动机的额定推力和停产状态对于预测燃料流量很重要。因此，这两个变量可以被用来预测任意额定推力和停产状态已知的发动机燃油流量，如JTD9-3发动机的情况。不同推力值（每台发动机4个推力值）下的燃料流量以及发动机停产状态构成一个矢量，然后利用多项式回归找出对应函数，对燃料流量和排放进行预测。将数据分为训练数据集和测试数据集（分别为60%和40%）。多项式回归分析的结果如图5（a）、（b）所示。JT9D-3发动机的额定推力约为193.5 kN，发动机目前已停产。将这两个变量输入多项式回归模型中以预测燃料流量和排放。这些预测的结果如图6（a）、（b）所示。图6（a）中的燃料流量ffuel采用多项式方程计算，其系数如式（10）所示。图6（b）中的一氧化碳（CO）排放指数fCO由式（11）计算得出。

2.3.3. 起落架力和力矩

参考文献[18,19]中给出了用于计算起落架力和力矩的数据和公式。飞机起落架已经简化为一个三轮车模型。在三轮车模型中，假定飞机具有三个起落架，将每个起落架视为一个非线性油压杆模型。飞机有两个主起落架（左和右）和一个前起落架。前起落架用于转向，但仅能通过两个主起落架进行制动。

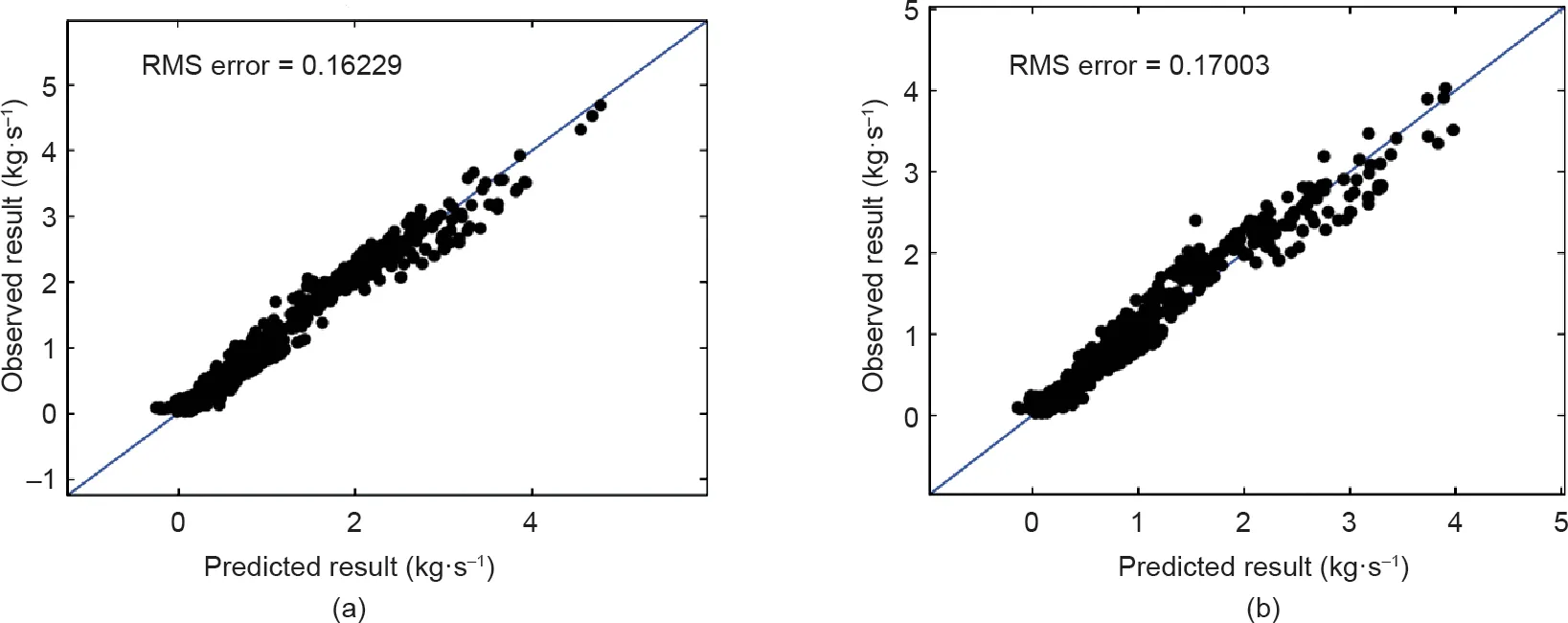
图5. 给定额定推力和非工作状态下燃料流量的预测结果。（a）训练数据结果；（b）测试数据结果。RMS：均方根。

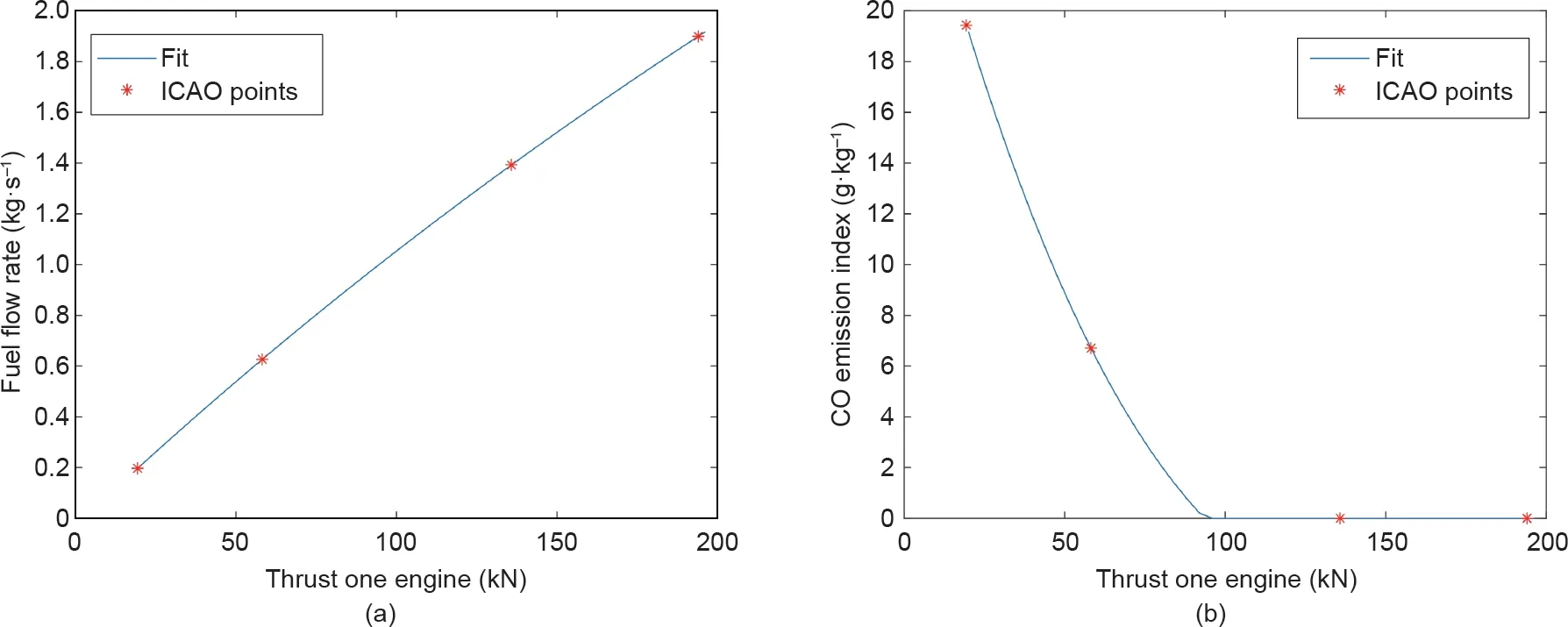
图6. 波音747-100飞机模型的JT9D-3发动机的预估。（a）燃料流量；（b）一氧化碳（CO）排放。

当飞机在地面上运动时，地面、轮胎和油压杆之间复杂的相互作用会产生影响飞机运动的力和力矩。由起落架产生的力和力矩分别在起落架的局部坐标系上计算，并将其转换到机体坐标系上。同其他部分的力和力矩一样，这些力和力矩取决于飞机的状态。计算起落架力和力矩的步骤如下。

·计算油压杆的压缩量和压缩率。对于每个起落架（前起落架、左起落架和右起落架）、压缩量和压缩率的推导如图7所示。

·计算垂向力。确定油压杆压缩量和压缩率后，就可以计算出力的三个分量（每个分量在起落架的局部机架中）。第一个分量用于计算垂向力Fz。垂向力承载飞机的重量，并在滑行期间为乘客提供舒适感。计算每个起落架的垂向力需先确定每个起落架的阻尼力和弹簧力，原因是起落架由非线性质量阻尼弹簧系统表示。弹簧力可从参考文献[18,19]中获得。与用于计算静态EPR的发动机数据一样，需对起落架数据（主起落架和前起落架的弹簧力和阻尼常数）进行多项式拟合。

图7. 油的压缩量和压缩率的推导。ΔSi和ΔS·i分别表示第i个起落架油的压缩量和压缩率（假定为三轮车模型，i = 1, 2, 3）。给定ΔSi和ΔS·i，图中所示为求出垂向力的必要步骤。垂向力沿着支柱从轮胎作用到飞机的机身。θB和φB分别是机身的俯仰角和倾斜角。xi、yi、zi是第i个起落架到机身轴重心的距离。

·计算侧向力。飞机滑行运动需要包括转弯的一系列操作。转弯运动是飞机不同部件的侧向力作用的结果。计算起落架侧向力的步骤如下：第一步需根据作用在轮胎上的垂向力确定轮胎的挠度。作用在轮胎上的垂向力与飞机的姿态有关。下一步需计算总侧向力，总侧向力是轮胎和运动方向之间的角度与轮胎挠度的乘积。最大总侧向力是轮胎垂向力的60%。

·计算阻力。阻力产生制动力，该制动力由主起落架施加，并在滑行期间使飞机停下或减速。在起落架中，阻力与制动力和摩擦力有关。制动力与常数KB= 0.263、飞行器质量和制动踏板偏转量有关。制动力的最大值取决于飞机的质量、滚动摩擦（对于干滑行道，μB= 0.4）和最大制动力常数（KBM= 0.834 + 4.167 ×μB）。摩擦力包含两个分量[爆发力（bof）和恒定的滚动摩擦力]。爆发力取决于飞机的地面速度（VG），其确定方法如下：

制动踏板的偏转已归一化在0到1之间。

·将力转换到机体坐标系。以上在每个起落架中计算出的力都要转换到机体坐标系中，以便计算机身的力和力矩。参考文献[19]所示的转换方程式如下（仅对小角度有效）：

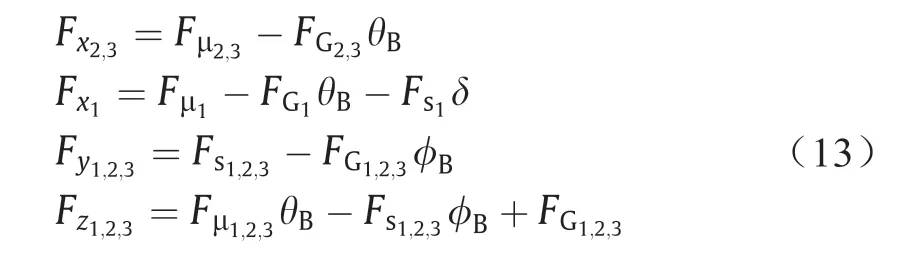
式中，θB和φB分别是机身的俯仰角和倾斜角；下角标1、2和3分别代表三个轮胎。Fμi、FGi和FSi分别是第i个轮胎的轮胎阻力、垂直油压杆支撑力和轮胎侧向力；δ是前轮转向角。通过三个起落架的力可以得到起落架的总力，如下所示：

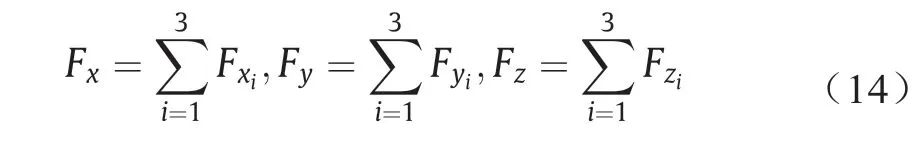
力矩方程式如下：

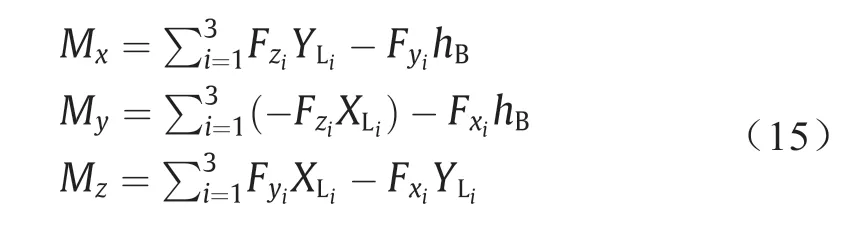
式中，XL和YL是飞机重心到完全伸展开的起落架末端的距离。hB= 17 + ΔSi，是飞机重心到轮胎与跑道接触所产生的法向力、侧向力和阻力的垂直距离。

2.3.4. 重力模型

有两种方法可以将重力产生的力加入飞机模型：第一种方法是利用平移加速函数[请参见式（5）]；第二种方法明确说明重力，然后将它们计入作用于飞机机身中的总力和力矩。我们使用后一种方法对这架飞机进行建模。假定重力直接作用在飞机的重心上，表明没有产生力矩。机体坐标系中沿x轴（Fgx）、y轴（Fgy）和z轴（Fgz）方向的力由下式给出：

式中，GSA是地面倾斜角度。一个重要的问题是如何将滑行道的地面坡度加入重力模型。如果飞机正在下坡行驶（正斜角），则气体将沿飞机的x轴产生正向力。此时地面倾斜角已忽略不计。

3. 飞机导航优化

导航系统由图8所示的方框组成，该系统允许飞机以最佳的方式在地面上移动。在每个机场中，调度程序通常都会提供航路点列表以及到达每个航路点的时间期限。这些航路点通常由最优调度算法[如具有时间窗的k条最快路径（k-QPPTW）算法[5] ]或机场多目标A*（AMOA*）算法[26]决定，且飞机需要以最佳方式遵循该调度。导航系统由一个外环控制器（由速度和航向算法表示）组成，用来确定参考点。与现有的开环方法[27-29]相比，这些参考点根据到下一个航路点的距离和时间限制进行在线计算。内环控制系统改变控制输入端，使飞机遵循参考点。当没有自动驾驶时，内环系统控制器通常由飞行员替代。内环系统控制器可以引导飞行员改变控制器输入，从而完成航路点之间的最佳滑行（使用最小数量的燃料）。因此，本部分的主要目标是开发一个最佳的控制器，以便在满足计划的同时使飞机（无论是通过完全自动化实现还是作为决策支持）通过滑行道。这里使用的方法是通过调整PID控制器的参数，使所设定的目标最小化，比如在遵循计划的同时尽可能减少所消耗的燃料。

3.1. 外环控制系统

外环控制系统决定了遵循指定计划时的航向和速度。本研究中未对外环控制系统进行优化。以下例子给出了确定参考航向和速度的过程。

示例1：假设调度程序向外环控制器提供以下信息，即在50 s内沿着500 m的距离直线移动。

外环控制系统将使用以下步骤确定速度和航向参考。

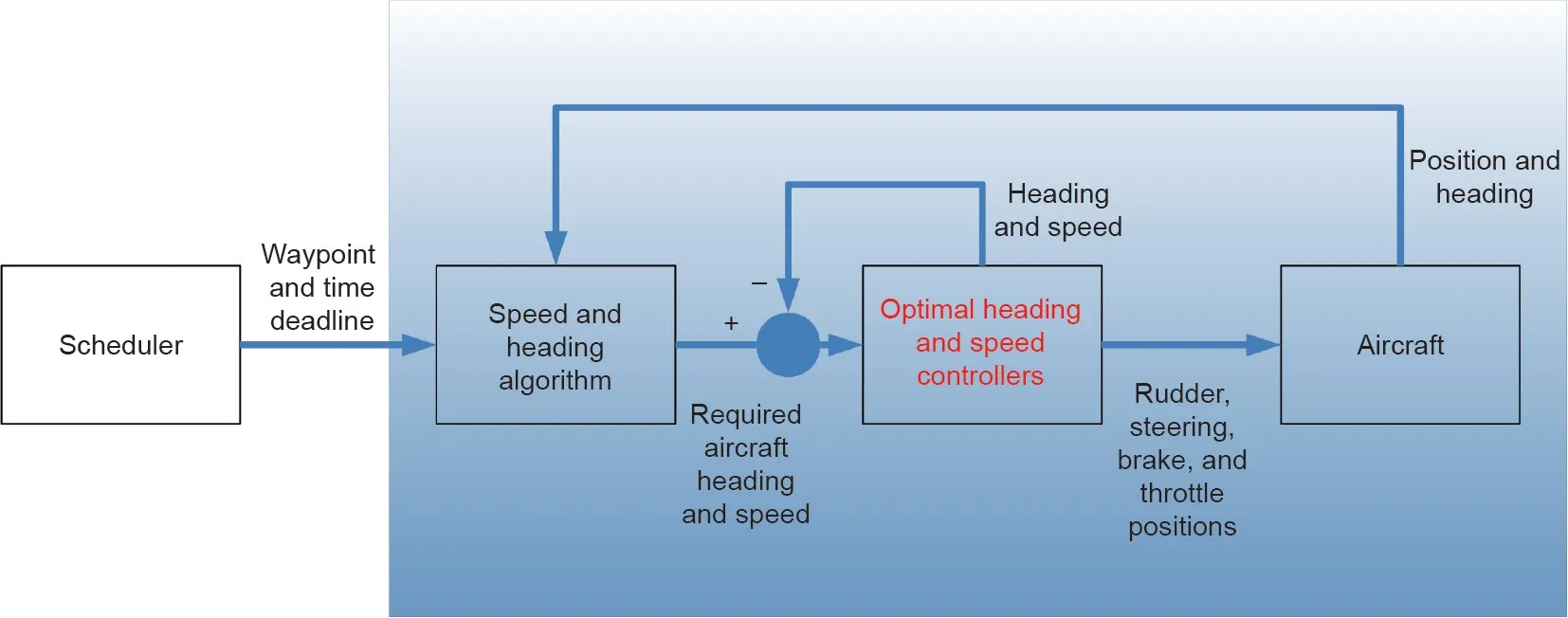
图8. 导航系统的方框图。

（1）确定航行段的类型。第一步是确定到达指定航路点的移动是转弯还是仅为直线段。在步骤2中计算出直线段的距离。

（2）计算到下一个航路点的距离（D）。

式中，（xp,yp）是航路点的坐标；（xc,yc）是当前飞机位置的坐标。

（3）假设飞机继续以当前的速度移动，计算预测的距离。预测距离（Dpred）如下：

式中，tr是到达航路点的剩余时间；Sc是当前的速度。将从到航路点的距离减去预测距离可以得到距离误差变量（E）。

（4）计算参考值。

式中，Sref是内部控制器的参考值；γ是确定参考速度的变化速率的常数。γ可以进一步被优化，但当它未被优化时，经反复试验可得γ= 10时的工作效果良好。

（5）在某些情况下，在末端指定速度约束（例如，当从直线段移动到转弯段时，将在该转弯段处使用恒定速度）。在这种情况下，利用以下算法可以计算参考速度。

（i）根据当前速度（Sc）得到最大减速度（1 m·s-2）和最大加速度（1 m·s-2），计算飞机从当前速度达到要求速度所需的时间（td）。这一时间可以通过方程td=ΔS/1求得，其中ΔS是Sc和航路点指定速度（Sf）之间的差的绝对值。

（ii）给定td并假定加速度或减速度恒定，计算该加速度或减速度满足航路点速度约束所需的距离（Dd）。计算方法如下：

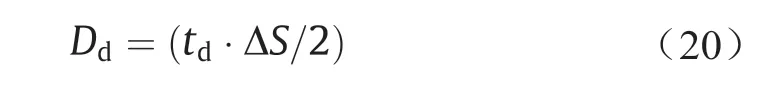
（iii）计算缓冲区距离（Db），以确定在满足航路点的速度约束时行驶的总距离。计算方法如下：

上述方程确定了通过加速或减速满足航路点的速度约束所需的距离。

（iv）如果抵达航路点所需的剩余时间大于td，则遵循正常控制程序[如步骤（i）～（iii）中的定义]，用D-Db代替D，用t-td代替t。

（v）如果剩余时间小于或等于td，则设置Sref=Sf。

上述提出的导航算法已经在以下几种情况下进行了测试，其中包括在50 s内从原点移动到(500 m, 0 m)处，且初始速度为5 m·s-1，最终速度为5 m·s-1。在上述情况下，该算法的测试结果如图9所示。

由图9分析可得，导航系统能够在规定的截止时间前到达指定的航路点。对于转弯段，同样使用上述导航算法，但以不同的方式计算距离。具体地说，假设转弯速度恒定（每秒4°），然后计算完成转弯所需的时间和开始转弯的时间。

3.2. 内环控制系统

到目前为止，讨论只涉及了如何确定参考（即航向和速度）。内部控制回路负责改变飞机输入（机舵、节流阀和制动器），以使飞机遵循参考点。内环控制由三套PID控制器组成，每个PID控制器分别操纵节流阀、制动器和机舵。对于制动器，只使用了比例控制器。为了避免同时使用制动器和节流阀的情况，控制块设定飞机仅在速度大于参考速度时使用制动器，而在当前速度小于参考速度时使用节流阀。PID控制系统的配置如图10所示。

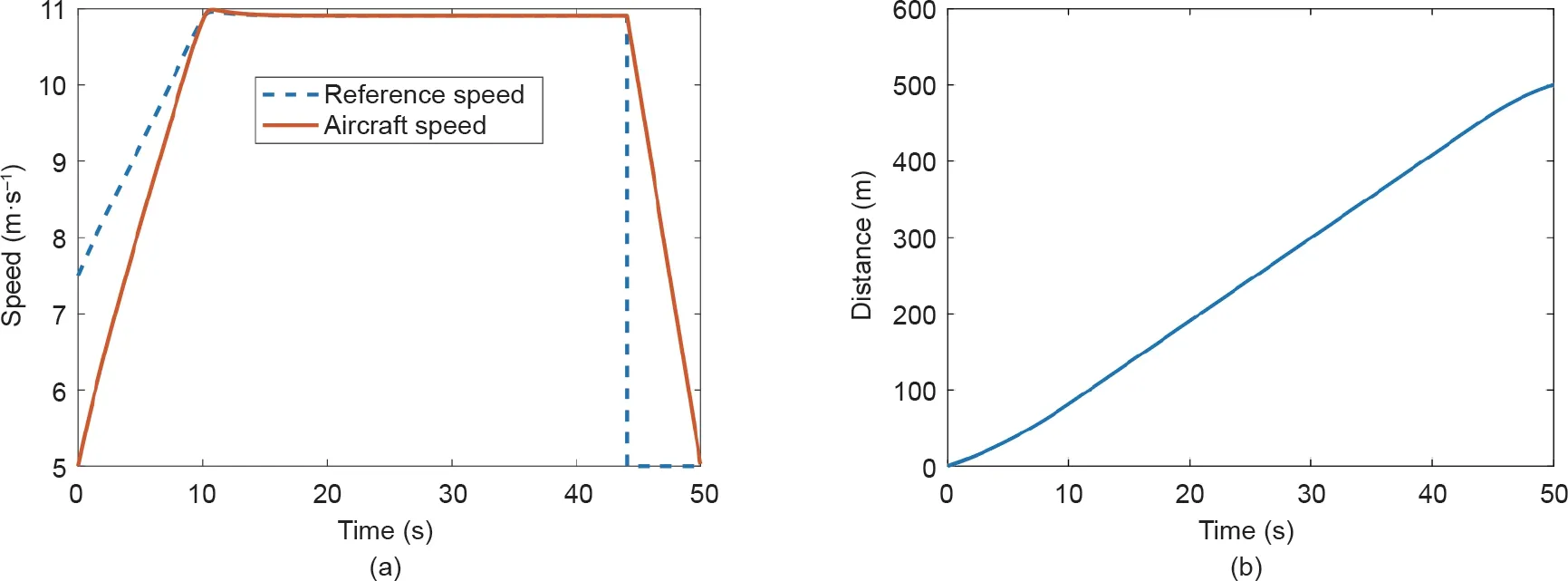
图9. （a）在规定最终速度的情况下，飞机的参考速度和实际速度（5 m·s-1）；（b）随时间变化的距离。

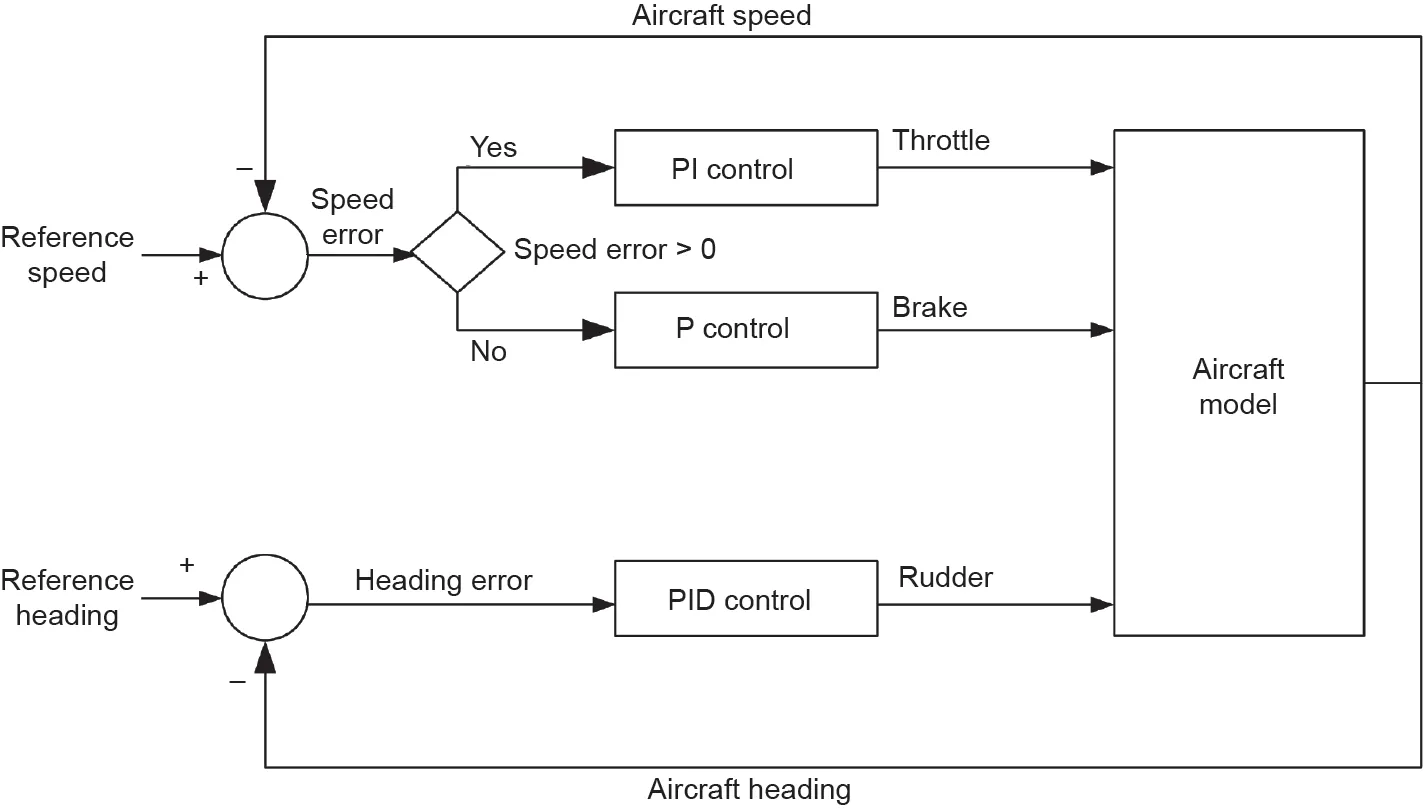
图10. 在内部控制回路中使用的PID控制系统的配置。P：比例，PI：比例-积分。

PID的参数需根据机场滑行的飞机情况进行优化。前文讨论的示例1是一个典型的情况。在MATLAB（MathWorks，美国）中使用遗传算法（GA）进行优化。性能标准取决于执行指定任务时所消耗的燃料。综上所述，优化算法所使用的目标函数采用如下方程式表示：

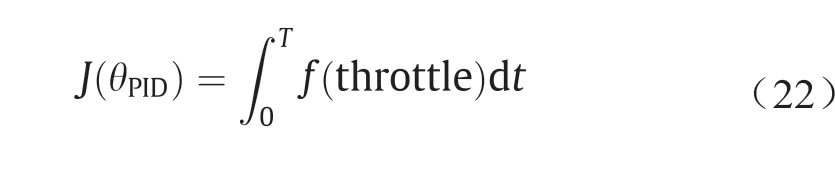
式中，J是目标；θPID表示PID增益；T表示完成由调度程序确定的计划所需的时间；而f(throttle)是根据图5得出的燃料消耗模型。如式（22）所示，节流阀大小取决于PID增益。本研究中的GA将种群大小设置为1000。平均而言，这些算法在第90万代时近似收敛。上述方法的一个缺点是，PID增益对于另一种方案而言可能不是最佳的。为了找到新情况的最优增益，优化算法需要重新运行，因此当存在大量不同情况时，可能会产生显著的计算成本。以英国曼彻斯特机场作为案例研究，调度程序包括大约9万个场景[图11（a）]。显然，获得9万套最优的PID增益是不可行的。为了解决这个问题，本文提出对情况列表进行聚类分析。假设集群的中心代表集群成员。优化只在表示集群中心的情况上进行，并且在整个集群成员中利用集群中心的PID增益。曼彻斯特机场案例的集群分析结果如图11（b）所示。

图11.（a）场景的散射图；（b）集群分析场景，其中用红点表示的6个集群是各集群的中心。

表2包括了在10个随机选择的情况中与其他两种方法相比的结果。第一个是从6个控制器中随机选择的一个控制器，第二个是为所选择的所有情况选择一个固定的控制器。

从表2中可以看到，使用聚类策略比对所有场景使用一个控制器具有更好的性能。对于控制策略违反调度程序或飞机限制的情况，应包括惩罚项（消耗2000 kg燃料）。1000个随机选择方案的三种不同控制策略所消耗的总燃料如表3所示。可以看出，平均而言，基于聚类的方法始终比使用固定控制器的策略性能更好。

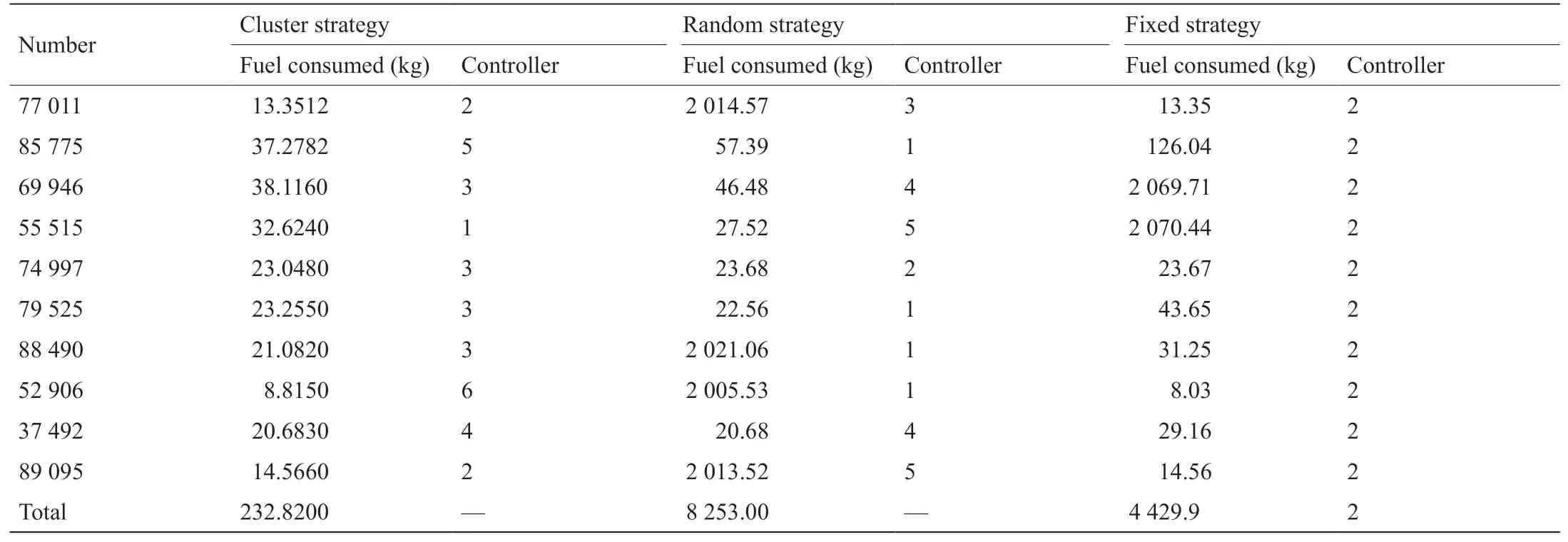
表2 三种控制策略的结果的比较

表3 随机选择的1000个情况的总燃料消耗量。控制器2在固定策略方法中提供了所有控制器中的最佳性能

4. 结果

本文在两种情况下对提出的方法进行了测试，并在以下小节中进行讨论。

4.1. 沿着矩形路径滑行

第一种情况是沿着矩形方向进行滑行，如图12所示。

选择飞机要遵循的路线图是为了考虑飞机在滑行期间的限制，如最大加速度、减速度和转弯速度的限制。该路线图包括两种滑行道。第一种是沿着矩形路径滑行，并假设没有地面坡度；第二种是沿着矩形路径滑行，并假设地面坡度为2°。坡度因素很重要，因为飞机在滑行过程中会经过地面坡度不同的滑行道。飞机的起点为矩形底部直线的左端。从该点开始，路径被分为8个不同的部分。路径的各段测量位置轨迹如图13所示。模拟数据段的截止时间见表4。

表4 模拟数据段的截止时间

滑行的结果如图14所示，由图可知飞机能够在遵守时间计划的同时遵循指定的路线。

4.2. 曼彻斯特国际机场滑行

在英国的一项真实滑行研究中对本文提出的算法进行测试，该研究中的路线为从英国曼彻斯特国际机场登机口滑行到跑道等待点（准备起飞）。机场滑行道布局和调度程序的优化路线如图15所示。航路点的坐标见表 5。

表5 从调度程序算法输出的航路点的地理坐标

如图16所示，在曼彻斯特国际机场滑行时，与传统的Ziegler-Nichols PID方法相比，文章提出的方法可以节省约11%的燃料。

图12. 用于测试的矩形图。

图13. 矩形路线试验中飞机的地理坐标。（a）无坡度滑行；（b）以2°坡度滑行。

图14. 通过坡度为0°的矩形段滑行的输入。（a）节流阀；（b）制动器；（c）机舵。

图15. 曼彻斯特国际机场的滑行道和跑道布局。优化的滑行路线以红色线突出显示。

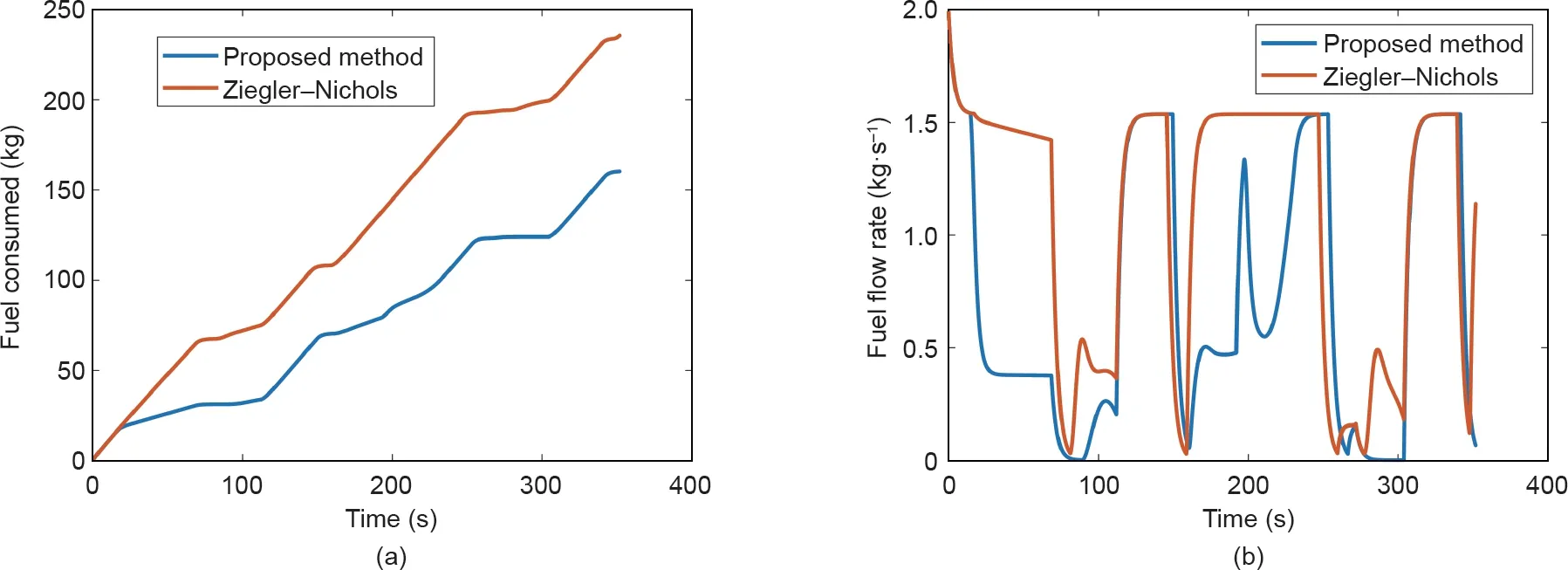
图16. 在曼彻斯特国际机场的航路点导航中使用优化的PID的燃料消耗与使用Ziegler-Nichols方法的PID的燃料消耗的对比。（a）通过曼彻斯特国际机场滑行时所消耗的总耗油量；（b）通过曼彻斯特国际机场滑行时的燃料消耗率。

5. 结论

本文提出了一种针对机场飞机在实际滑行过程中的最佳导航方法。虽然该算法是基于波音747-100飞机模型进行开发和测试的，但所提出的方法是通用的。该方法包括使用GA优化PID增益，从而使飞机以最优的方式进行滑行。这种方法可以用于全自动滑行的飞机，也可以作为飞行员的决策支持，即在飞行员以最佳的方式执行操作时，向其提供能够满足调度程序的时间限制的最佳控制输入。在将其用于解决实际滑行问题时，与传统的Ziegler-Nichols PID控制器相比，该方法可以节省高达11%的燃料。本文的研究结果是在世界范围内实现飞机从门到门运行中的一个重要飞跃。这种方法不仅有效地提高了飞机的操作效率，而且还有助于减少飞机的燃料消耗（燃料消耗是造成温室气体排放的重要因素）。未来的研究需量化飞机地面运动中许多不确定性的影响，如飞行员的操作和飞机的不同配置。

Acknowledgements

This work was funded by the UK Engineering and Physical Sciences Research Council (EP/N029496/1, EP/N029496/2, EP/N029356/1, EP/N029577/1, and EP/N029577/2).

Compliance with ethics guidelines

Olusayo Obajemu, Mahdi Mahfouf, Lohithaksha M.Maiyar, Abrar Al-Hindi, Michal Weiszer, and Jun Chen declare that they have no conflict of interest or financial conflicts to disclose.

Appendix A. Supplementary data

Supplementary data to this article can be found online at https://doi.org/10.1016/j.eng.2021.01.009.