基于LS-SVM的结构损伤识别仿真分析

罗丽燕 王添龙

（1广东省建筑设计研究院有限公司；2东莞市路桥投资建设有限公司）

基于LS-SVM的损伤识别，借助LS-SVM lab工具箱，主要使用分类和回归函数对结构进行损伤识别。LS-SVM损伤识别方法流程图如图1。

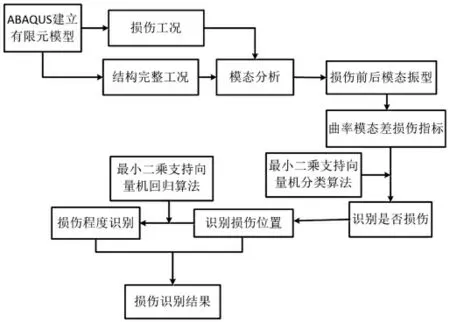
图1 LS-SVM的损伤识别流程

1 曲率模态损伤识别理论

梁的振动微分方程为：

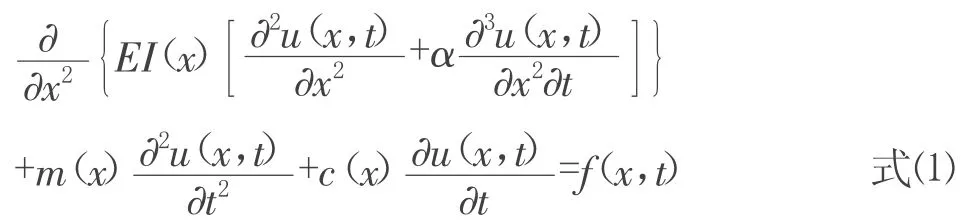
其中，u（x，t）表示t时刻在x处的横向振动位移，m(x)表示单位长度梁的质量，α是刚度系数。

式⑴的简谐运动形式为：

其中U(x)为振型函数，与位置有关；T(t)为简谐运动函数，与时间有关。

将式用各阶位移模态φi（x）来表示[1,4]：

其中qi（t）表示模态坐标。

由文献[12]知梁振动的微分方程的解为：

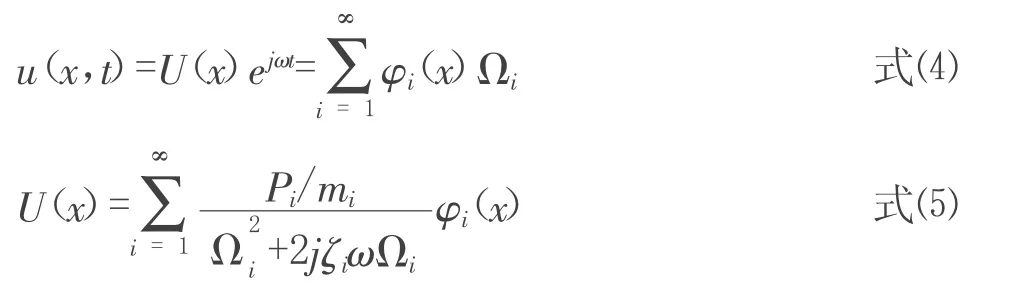
则由曲率的定义可得：

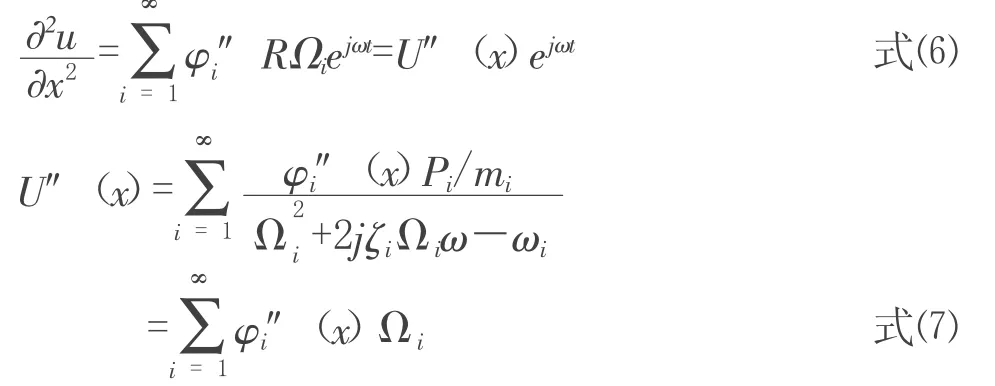
其中，φi表示各阶位移模态，Δl为相邻两测点间的距离。

曲率模态差是结构损伤前后曲率模态值的差的绝对值[11]，公式如下：

2 LS-SVM原理

LS-SVM作为SVM的一种改进算法，它提高了SVM的分类正确率，弥补了SVM在某些方面的不足。所以推广LS-SVM的研究应用很有必要[3]。已知一组训练集：

（x1，y1），…，（xl，yl），x∈Rn，y∈R对于非线性问题，可以用非线性变换φ（.）将输入向量映射到高维特征空间，转化为类似的线性回归问题。LS-SVM最小化目标函数为：

其中，w为权向量；γ为正则化参数；ei为样本训练误差。

用拉格朗日法求解：

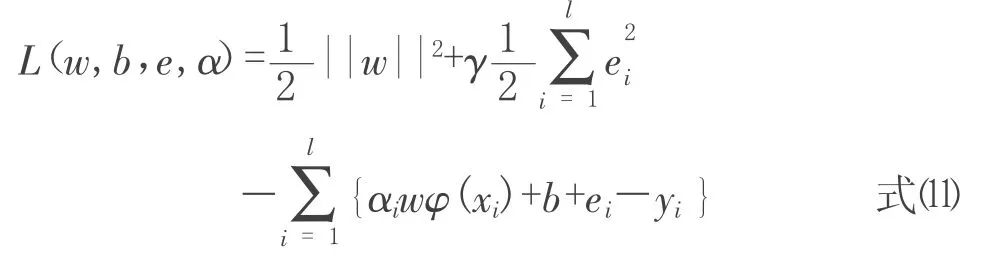
其中αi（i=1,2,…,l）是拉格朗日乘子。对w，b，ei，αi求偏导，根据优化条件，可得到：

其中，αi=γei，wφ（xi）+b+ei－yi=0

定义核函数K=（xi,yi）=φ(xi)·φ(xj)是满足条件的对称函数。根据文献[5]，优化问题转化为求解线性方程：

最后用最小二乘法求出α和b得到LS-SVM回归函数为：

K（x,xi）=ϕ（xi）·ϕ（x）称为核函数，在本文中选择的是RBF函数。

RBF函数（径向基核函数）：

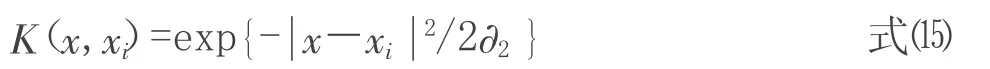
和SVM一样，LS-SVM使用核函数K（x,xi）代替高维空间的内积形式可以解决高维计算问题[6]。

3 钢桁架数值模拟分析

用一长度为2.5m，宽度和高度均为0.5m的空间钢桁架作为有限元分析模型。结构及结构损伤杆件编号如图2所示。

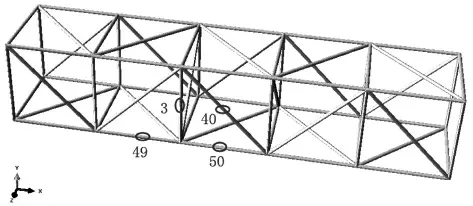
图2 模型及损伤杆件编号

该结构共有66根杆件，分成66个单元，使用弹性模量折减的方式模拟杆件损伤。根据相关计算分析，输出结构的模态频率和振型，算出结构的曲率模态差值，一共有三种损伤类型，6种损伤工况，损伤工况如表1所示。

表1 损伤工况

3.1 损伤位置识别结果

利用LS-SVM分类算法和回归算法分别实现损伤位置和损伤程度识别功能，针对各损伤工况，进行损伤位置识别时，采用各工况发生损伤程度为10%、15%、20%、30%、35%、40%、50%、60%、70%的样本作为LS-SVM的训练样本，以损伤程度为25%、45%、65%的样本作为LS-SVM的测试样本，算出结构在三种不同损伤位置类型下不同损伤程度的模态曲率差值，作为LS-SVM的输入参数，结构的损伤位置作为LS-SVM的输出参数。构造好训练样本和测试样本后即可使用LS-SVM对训练样本进行分类，检验LS-SVM对结构损伤位置的识别能力。其损伤识别结果如表2所示。

表2 损伤位置识别结果

3.2 损伤程度识别结果

在建立的LS-SVM模型基础上，可对损伤工况出现25%、35%、55%、65%的损伤程度进行预测，进行损伤程度识别时，以结构各工况发生损伤程度为10%、15%、20%、30%、35%、40%、50%、60%、65%、70%、75%的 样 本 作 为LS-SVM的训练样本，以发生损伤程度为25%、45%、55%、65%的样本作为LS-SVM的测试样本，其程度损伤识别结果如表3所示。

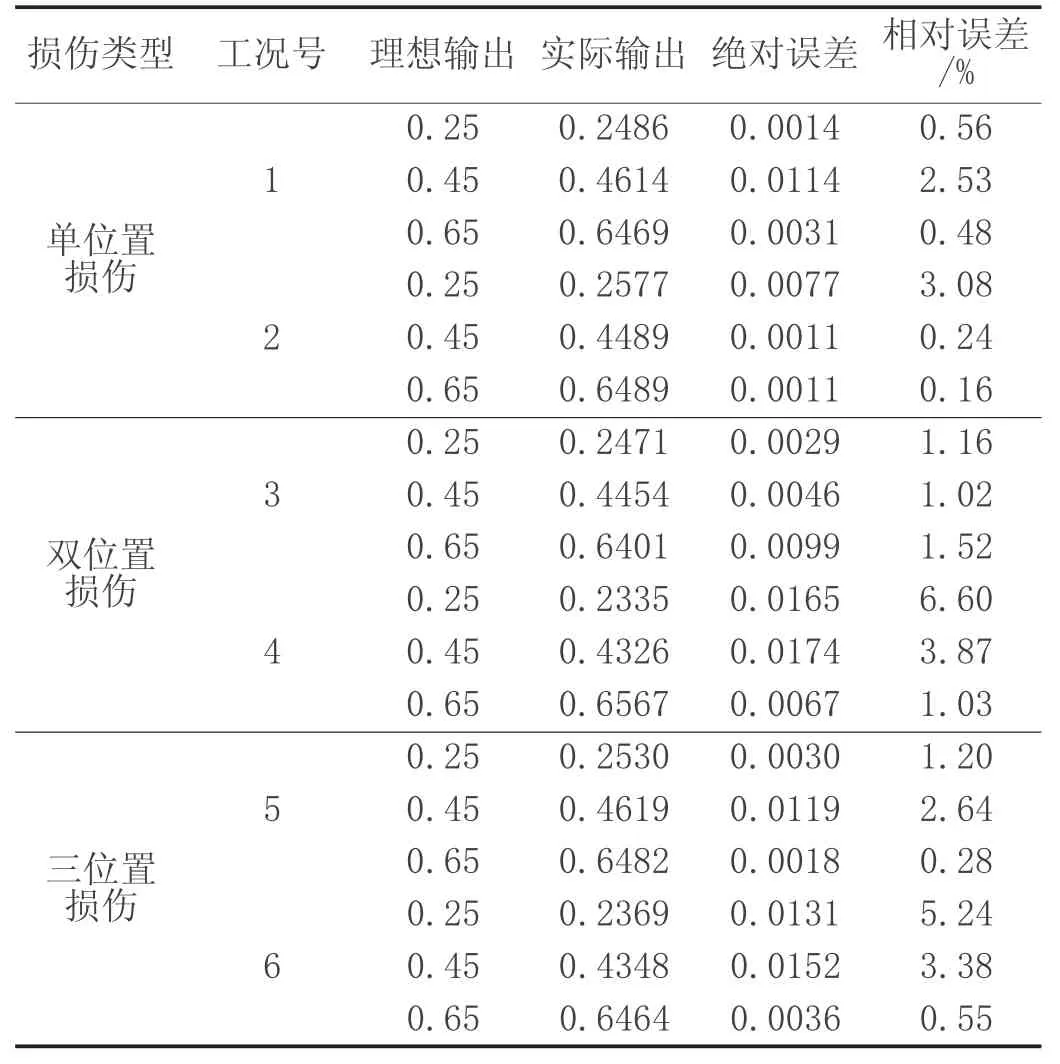
表3 损伤程度识别结果

4 结论

通过建立一个空间钢架的有限元模型，用LS-SVM的分类和回归模式识别方法对结构进行了损伤识别，均取得良好的识别结果。可得出以下结论：

⑴使用LS-SVM的分类算法和回归算法对模型算例进行损伤识别，说明了LS-SVM具有很好损伤定位和损伤程度识别效果。

⑵LS-SVM与模态分析方法与LS-SVM有机结合，可准确地对结构进行损伤位置的定位和损伤程度的识别，还可以有效地识别出结构同时发生单位置、双位置、甚至多位置处的多处不同程度损伤的损伤位置和损伤程度。