去蜂窝大规模MIMO系统中预编码算法研究
朱翠涛,赵瑶
(中南民族大学 智能无线通信湖北省重点实验室,武汉 430074)
为提升用户覆盖率和用户体验,2017年NGO等人提出了去蜂窝大规模MIMO的概念[1-2],结合集中式大规模MIMO和分布式大规模MIMO的优点,打破传统小区的概念,不存在所谓的边缘用户,因此可实现更加均匀的覆盖[3].虽然去蜂窝大规模MIMO技术有着广阔的应用前景,但是仍然存在一些需要解决的问题.例如,如何选择合适的预编码算法,在获得较好系统频谱效率的同时降低计算复杂度[4].
在去蜂窝大规模MIMO系统的下行链路发送端,信号在传输过程中会受到用户之间的干扰,导致系统性能的下降.而由于在用户端较难采取有效手段消除用户间干扰,因此需在发送端进行预编码处理.目前,在去蜂窝大规模MIMO中,常用的预编码算法有共轭波束成形 (Conjugate Beamforming,CB)预编码[5]、迫零(Zero-forcing,ZF)预编码[6-8]、正则化迫零(Regularized Zero-forcing,RZF)预编码[9]以及最小均方误差(Minimum Mean Square Error,MMSE)预编码[10-11].其中,CB预编码比较简单,但存在用户之间的干扰.与此相反,ZF预编码、RZF预编码以及MMSE预编码都可以消除用户之间的干扰,但涉及矩阵求逆运算,增加了运算量且提升了实际通信系统中硬件实现难度[12].因此,减少矩阵求逆的运算量也就降低了预编码算法复杂度.在大规模MIMO系统中,文献[13]给出了截断多项式扩展预编码算法,该算法利用矩阵多项式代替矩阵求逆,可以降低系统复杂度,但需要处理复杂的参数优化问题.文献[14]中利用高斯塞尔德迭代把矩阵求逆问题转化成求解方程式的解,降低了计算复杂度.虽然在大规模MIMO系统中关于低复杂度的预编码算法已经存在一些研究成果,但在去蜂窝大规模MIMO中却研究较少.
因此,在去蜂窝大规模MIMO系统中,提出一种基于Neumann级数(Neumann Series,NS)的低复杂度预编码算法.该算法首先计算ZF预编码中Hermitian矩阵即信道矩阵转置与信道矩阵共轭的乘积,为了满足Neumann级数收敛条件对该矩阵进行加权处理,接着通过Neumann级数多项式展开法,对前有限项进行求和,最后近似得到正定Hermitian矩阵的逆矩阵.NS预编码没有复杂的参数,采用多项式迭代过程代替ZF预编码矩阵的求逆运算,有效降低了计算复杂度.
1 系统与信号模型
如图1所示,去蜂窝大规模MIMO系统由一个中心处理单元(Central Processing Unit,CPU)、M个接入点(Access Point,AP)和K个用户终端(User Equipment,UE)组成,满足M>K,每个AP和UE均为单天线配置,并随机分布在一个给定的区域内.其中,所有的AP通过回程链路与CPU连接,并在同一个频带资源内同时服务于所有UE,该系统中所有的AP和UE都以时分双工(Time Division Duplex,TDD)模式进行工作,AP和UE之间的信道具有互易性.
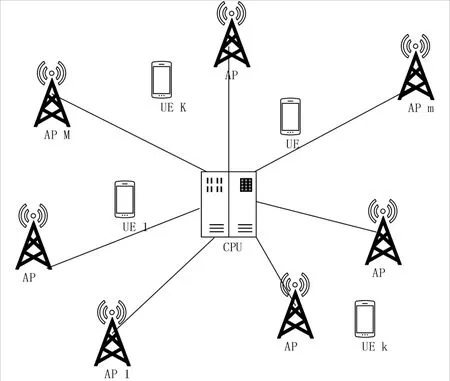
图1 去蜂窝大规模MIMO系统Fig.1 Cell-free massive MIMO system
在去蜂窝大规模MIMO系统下行链路中,第k(k=1,2,…,K)个UE的接收信号为:
(1)
其中,Hmk表示第m(m=1,…,M)个AP与第K个UE之间的信道系数,xm表示第m个AP的发射信号,nk表示第k个UE处的加性噪声,服从均值为0,方差为1的复高斯分布.
由于AP和UE之间的信道具有互易性,可通过上行链路训练获取下行链路的信道状态信息(Channel State Information,CSI).根据文献[2]可知,第m个AP与第k个UE之间的信道系数由大尺度衰落和小尺度衰落两部分组成:
(2)

在上行链路导频训练中,CPU随机分配导频给所有UE,接着所有的UE同时发送导频给所有AP,最后在AP处进行信道估计.则第m个AP处的MMSE信道估计为:
(3)

(4)
在去蜂窝大规模MIMO系统下行链路中,UE信道信息的获取和预编码处理都是在AP上独自执行的。当使用线性预编码处理时,第m个AP发射的信号为:
(5)
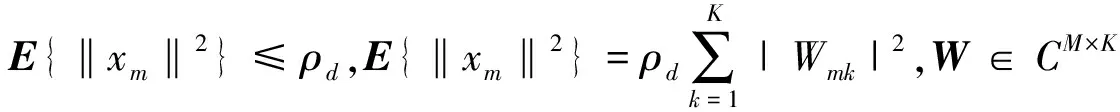
2 基于Neumann级数预编码
2.1 迫零预编码
在去蜂窝下行链路中,根据上行链路AP上所获得的CSI,采用ZF预编码技术进行信号预处理,定义ZF预编码算法的预编码矩阵为:
WZF=BZFP,
(6)

因此,在下行链路中,采用ZF预编码技术,更新公式(1),第k个UE的接收信号为:
(7)
式(7)中接收信号被划分为四部分,第一部分为有效信号,第二部分为其他用户间的干扰,第三部分为信道误差造成的干扰,第四部分为信道噪声.
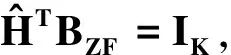
(8)
考虑信道估计以及ZF预编码的计算,并参考文献[16],第k个UE的频谱效率为:
(9)
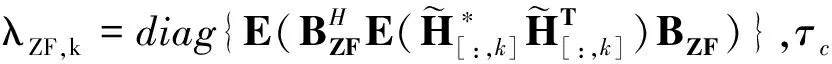
由于ZF预编码中存在大矩阵求逆计算,随着UE数量K和AP数量M的增加,其复杂度也随之增加。为了降低该复杂度,避免矩阵的求逆,提出了一种基于NS算法的改进预编码算法.
2.2Neumann级数多项式展开法
Neumann级数直接对矩阵的逆进行估算,假设K阶方阵Z满足:
(10)
其中,I,0k分别为K阶单位矩阵和K阶零矩阵,则方阵Z的逆可以使用Neumann级数进行展开,则:
(11)
(12)
化简得:
(13)
由式(13)可知,对于给定的迭代次数N,近似ZZF-1的精准度取决于(IK-DZZF)矩阵特征值的大小,若要使算法的收敛性快,则D的特征值必须小。从这个思路出发,取矩阵ZZF每个对角元素的倒数所形成的对角矩阵作为D,D的表达式可表示为:
D=diag(1/ZZF(1,1),1/ZZF(2,2),…,1/ZZF(k,k)).
NS预编码算法步骤如下:

步骤2不满足收敛条件,则进行加权处理,获得矩阵DZZF;
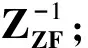
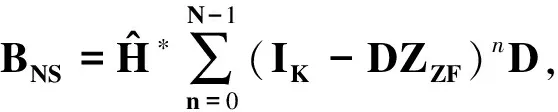
WNS=BNSP.
3 复杂度分析
通过理论方法比较ZF预编码和NS预编码的复杂性,由于加法的运算量相对于乘法来说很低,因此仅计算各算法的乘法运算量,另外因为除矩阵求逆过程外其他部分运算量相同,所以仅对矩阵求逆进行复杂度的比较.ZF预编码的复杂度是3K3+2K2,NS预编码的复杂度如表1所示.

表1 NS预编码复杂度Tab.1 NS precoding complexity
如图2所示,M=100时NS预编码的计算复杂度随着N的增加而增加,当N<5时,NS预编码的复杂度小于ZF预编码,而当N=5时,NS预编码的复杂度接近ZF预编码的复杂度.但是,在实际的通信系统中矩阵求逆计算对硬件的要求较高,实现起来相比于矩阵乘法困难,所以NS预编码更适用于实际的通信系统.
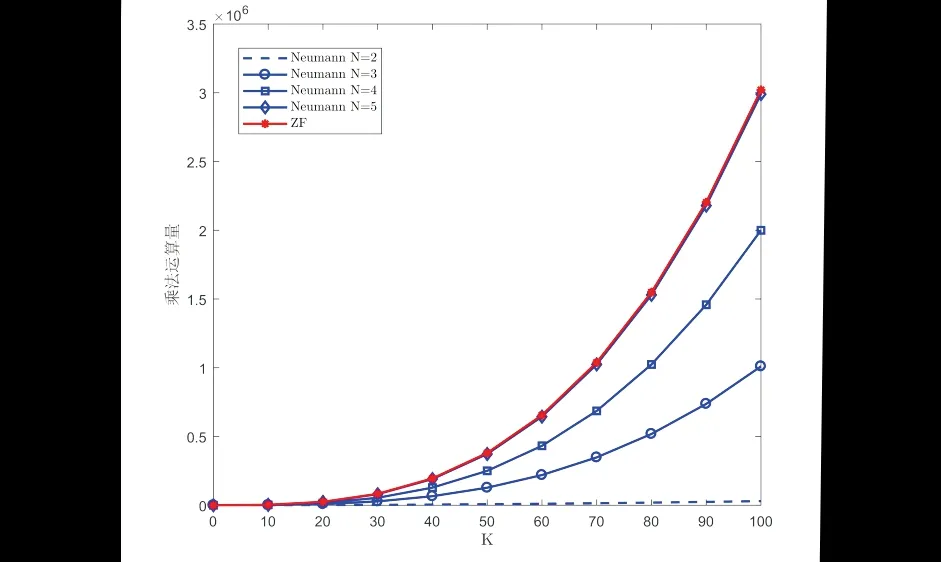
图2 计算复杂度分析Fig.2 Computational complexity analysis
4 仿真分析
为了验证所提出的NS预编码算法理论分析的正确性以及算法的性能,本实验将对NS预编码算法与ZF预编码算法进行性能比较.在一个由M个AP与K个UE组成的1000 m×1000 m的系统中,所有AP和UE的位置都是随机生成的,系统的仿真参数如表2所示.
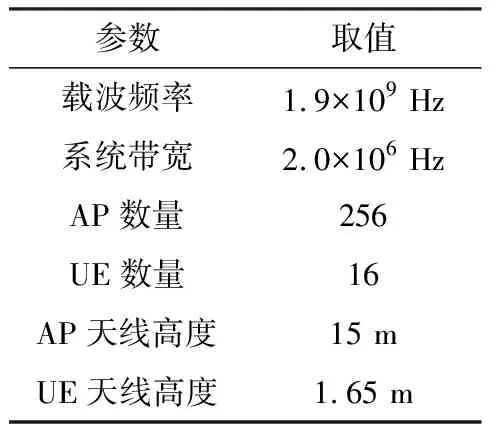
表2 系统仿真参数Tab.2 System simulation parameters
图3为CB、NS以及ZF预编码算法的用户频谱效率累积分布图,从图中可以看出,当AP和UE数量为定值时,ZF预编码算法和NS预编码算法的系统性能远远优于CB预编码.而且,随着迭代次数N的线性增加,尤其是当N=4时,NS预编码算法的累积分布曲线接近于ZF预编码.
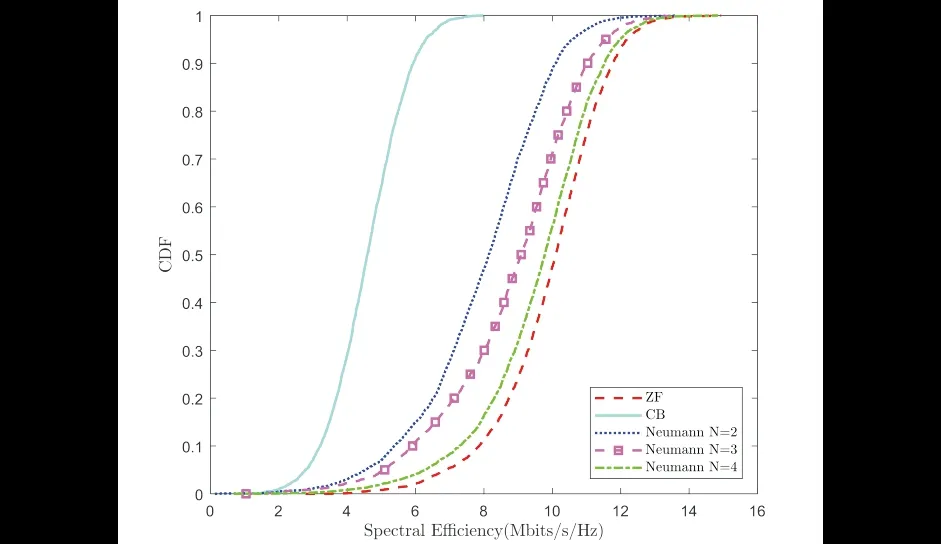
图3 用户频谱效率累积分布图Fig.3 Cumulative distribution of user spectrum efficiency
由图4可以看出,当K=16时,系统的平均频谱效率随着AP数量M的增加而增加,NS预编码的平均频谱效率也随着迭代次数的增加而增加.当迭代次数N=4时,ZF预编码平均频谱效率与NS预编码的最大差值为1.4309兆比特/秒/赫兹,最小差值为0.2455兆比特/秒/赫兹,NS预编码的平均频谱效率随着M的增加逐渐近似ZF预编码的平均频谱效率.
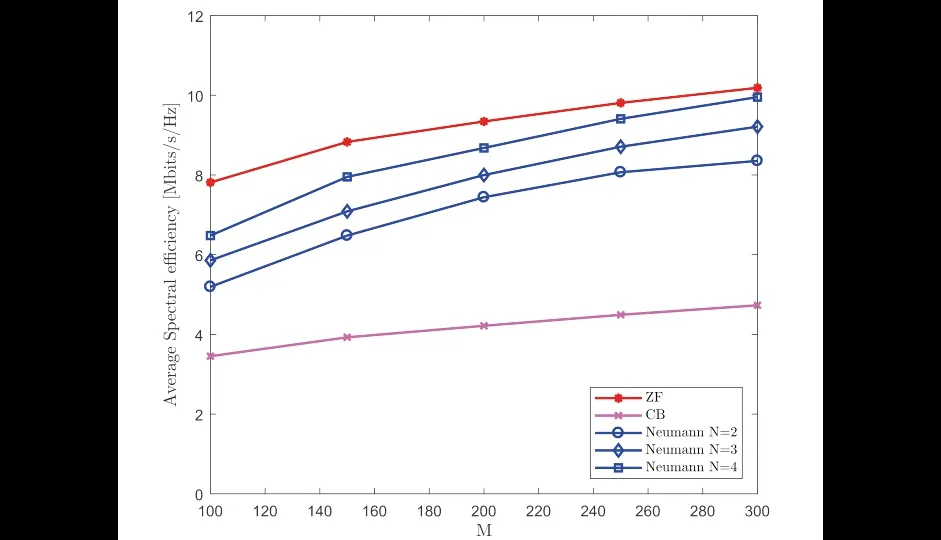
图4 接入点数量对系统平均频谱效率的影响Fig.4 The influence of the number of access pointson the average spectrum efficiency of the system
图5为下行链路发射功率对系统平均频谱效率的影响,随着发射功率的增大,两种预编码算法的平均频谱效率值较为稳定.当迭代次数N=4时ZF预编码与NS预编码的平均频谱效率之差基本保持在0.5兆比特/秒/赫兹左右,两者之间的差距较小.
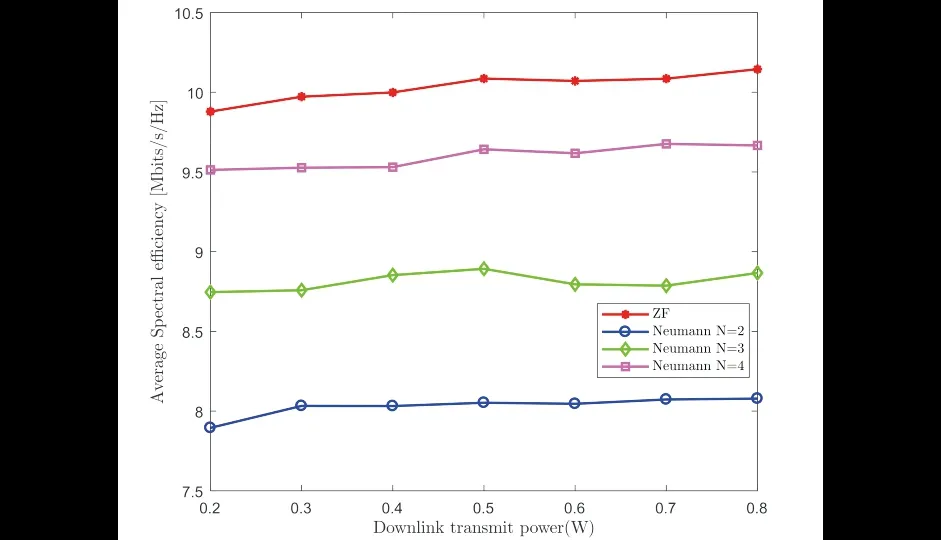
图5 下行链路发射功率对系统平均频谱效率的影响Fig.5 The influence of downlink transmit power on the average spectrum efficiency of the system
5 结语
综上所述,针对去蜂窝大规模MIMO系统中ZF预编码计算复杂度高的问题,提出一种基于NS低复杂度预编码算法.该算法将ZF预编码中矩阵的逆矩阵用一个具有N项的矩阵多项式代替,避免矩阵求逆的过程.通过对两种预编码算法的复杂度分析,当迭代次数N<5时,NS预编码算法相比于ZF预编码算法系统复杂度低.仿真结果证明,NS预编码算法在降低复杂度的同时用户平均频谱效率与ZF预编码算法相比差距较小,可以近似代替ZF预编码算法.

