面向质量设计的Kriging组合建模技术

肖甜丽，马义中，林成龙

(南京理工大学 经济管理学院，江苏 南京 210094)

0 引言

现代质量工程中，产品的稳健设计通常依赖于高保真的数值仿真。然而，这些高保真的数值仿真往往因耗费大量时间，造成计算成本过高。为减少计算成本，借助计算机试验构建代理模型，以替代昂贵的高保真数值仿真，受到了广泛关注[1-3]。Kriging模型作为计算机试验中常用的代理模型之一，首次由SACKS等[4]应用于计算机试验。一个Kriging模型主要由趋势项和高斯随机过程项两部分组成，分别用均值函数和协方差函数来表示。在均值函数已知的情况下，协方差函数中的核函数对Kriging模型的拟合效果起决定作用。工程设计中，最广泛使用的核函数为高斯核函数。XIONG等[5]利用高斯核函数构造的Kriging模型来建立方差模型和均值模型，优化了非线性信号响应系统;同样地，ACAR[6]的研究表明，高斯核函数的预测性能优于指数核函数和线性核函数。然而，由于高斯核函数的平滑度对于许多实际过程来说是不现实的，STEIN[7]建议使用Matérn核函数而不是高斯核函数。值得注意的是，最优核函数高度依赖于具体问题，没有某个单一核函数对所有问题都是最优的。现有大部分关于Kriging模型的研究基本都是预先指定核函数，这可能导致所建立模型的预测效果较差。而利用不精确预测模型所获得的优化参数组合，无法保证质量设计方案的可靠性。

为避免错误使用不合适的核函数，可将多个不同的核函数构成的Kriging模型组合为一个整体，即Kriging组合模型。Kriging组合模型不是为特定问题选择某个最佳核函数，而是充分利用多个核函数的预测能力来构建一个具有普适性的强大集成模型[8-10]。PALAR等[11]利用组合建模技术，将Kriging模型中的高斯、Matérn3/2和Matérn5/2三种常见的核函数组合在一起，并通过一个空气动力学实例证明了所提Kriging组合模型在精度上更为稳健，能够实现与最佳单个核函数相似的性能;PALAR等[12]通过试验分析表明考虑多个核函数的Kriging组合模型提高了有效全局优化的稳健性和预测性能;GINSBOURGER等[13]提出将指数核函数和高斯核函数相结合来构建Kriging组合模型，避免了Kriging核函数错误指定的风险。

Kriging组合模型的一般表现形式为多个子模型的线性加权组合。因此，组合建模过程中包含两个关键问题：①如何确定子模型集；②如何确定子模型的权重。现有关于子模型集的研究大都是预先指定，而后采用一定的方式加权组合。然而，并非所有子模型都能显著提升组合模型的预测精度，有些子模型可能不合适。因此，在构建组合模型前，有必要从候选子模型集中剔除冗余子模型。ZHOU等[14]提出利用逐步回归对构成组合模型的4个候选子模型进行选择;OUYANG等[15]指出文献[14]所提的模型选择方法是一次性的选择过程，从方法的稳健性方面无法反映每个子模型的优势和劣势，并提出基于Bootstrap重抽样法来分析每个子模型的性能。上述模型选择方法均未考虑使用者的先验知识。随机搜索变量选择(Stochastic Search Variable Selection, SSVS)法主要用于回归模型中变量的选择，不仅考虑了统计意义，还将使用者的先验知识通过先验假设融入到变量的选择过程[16]。因此，本文通过借鉴SSVS法的思想，提出了在Kriging组合建模中的核函数选择方法。

在确定Kriging组合模型的子模型集后，还需计算各子模型对应的权重。按照子模型权重的确定方法，可将组合模型分为全局组合模型[8-9]和局部组合模型[17-18]两类。全局组合模型在整个设计空间具有不变的权重因子，而局部组合模型则具有随预测点的位置变化而变化的权重因子。尽管局部组合模型比全局组合模型具有更高的精度，但其在设计优化中的计算成本远高于全局组合模型。考虑到计算经济性，全局组合模型更适合应用于实际的设计优化过程。然而，该方法在整个设计空间中只有一组权重因子，这可能导致设计空间的某些区域无法获得很好的预测。因此，为兼顾多个区域的预测精度，本文考虑通过划分多个子组来优化权重因子，提出在Kriging组合建模中基于K均值聚类的多组权重因子法。

1 Kriging代理模型

为构建Kriging组合模型，本文在普通Kriging(Ordinary Kriging, OK)模型的基础上，考虑了3个广泛使用的核函数，即高斯核函数、Matérn3/2核函数和Matérn5/2核函数。

1.1 Kriging模型

假设设计空间具有n个观测样本点，样本输入矩阵表示为x=(x1,x2,…,xn)T，对应的响应为y=(y(x1),y(x2),…,y(xn))T。其中，第i(i=1,…,n)个输入值xi=(xi1,xi2,…,xip)，p为输入因子的维度，则普通Kriging的模型形式为：

y(xi)=μ+Z(xi)。

(1)

式中：μ为Kriging近似的均值，用于代表总体趋势;Z(xi)为中心化的平稳高斯过程，用于插值。假定任意的两个点xi和xj，则y(xi)和y(xj)之间的协方差为cov[Y(xi),Y(xj)]=cov[Z(xi),Z(xj)]=σ2R(xi,xj)。其中，R(xi,xj)为核函数(相关函数)，可由超参数θ=(θ1,θ2,…,θp)来进一步确定；σ2表示过程方差。

对于任意一个新的输入x*，OK模型的最优线性无偏预测为：

(2)

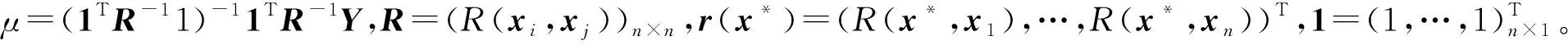
1.2 Kriging模型的核函数

1.2.1 高斯核函数

高斯核函数的一般表示形式为：

(3)

式中：h=‖xi-xj‖，i和j分别表示两个不同的设计点;θ=(θ1,…,θd)为核函数的超参数。

1.2.2 Matérn类核函数

Stein基于Matérn的工作提出了将Matérn类函数应用于Kriging模型。Matérn核函数的一般表示形式为：

(4)

式中：v≥1/2表示形状参数;Γ为Gamma函数;κv为第2种改进的贝塞尔函数。通过使用特定的v值可构造特定的Matérn核函数。根据RASMUSSEN等[19]对于机器学习的高斯过程研究发现，Matérn类核函数中最有趣的两个特例为v=3/2和v=5/2。

当v=3/2时，Matérn核函数的表示形式为：

(5)

当v=5/2时，Matérn核函数的表示形式为：

R(θ,h,v=5/2)=

(6)

以上两种Matérn核函数广泛用于实际过程建模。因此，除高斯核函数外，本文还选择Matérn3/2和Matérn5/2作为Kriging组合模型的候选核函数。

2 Kriging组合模型的构建方法

2.1 基于SSVS法的Kriging核函数选择

首先将组合模型表示为：

y=β1f1(x)+…+βmfm(x)+ε。

(7)

进一步地，将f1(x),f2(x),…,fm(x)分别替换为M1(x),M2(x),…,Mm(x)，则式(7)可表示为：

y=β1M1(x)+…+βmMm(x)+ε。

(8)

式中M1(x),M2(x),…,Mm(x)表示由不同的单个候选核函数所建立的Kriging子模型。

给定一组试验数据集{(x1,y1),(x2,y2),…,(xn,yn)}，则对应的线性回归模型可表示为：

(9)

式中：Mj(xi)(i=1,2,…,n;j=i=1,2,…,m)为第j个子模型在xi处的预测值；ε=(ε1,…,εn)T服从均值为0，协方差为σ2In的多元正态分布。为获得xi处各子模型的预测值，本文以除第i次试验运行外的样本数据{(x1,y1),…,(xi-1,yi-1),(xi+1,yi+1),…,(xn,yn)}作为训练集来构建由不同的单个候选核函数所建立的Kriging子模型，而后利用所建立的各子模型来预测xi处的输出。

在GEORGE等[16]提出的随机搜索变量选择法的基础上，将由单个核函数所构建的Kriging子模型看作单个变量以实施核函数的选择。子模型的显著与否，可通过在式(8)中引入指示性变量γj=0或1来判断。首先假设γj先验分布为

P(γj=1)=1-P(γj=0)=pj。

(10)

进一步地，将模型系数βj的先验分布表示为一个混合正态分布

(11)

式中：τj取较小值，表示当γj=0时βj的取值紧靠0附近，对应的子模型是不显著的；cj取较大值，表示当γj=1时βj具有非0的估计值，对应的子模型是显著的。残差方差σ2独立于指示性变量γj和模型系数βj，其先验分布假设为一个逆伽马分布

σ2～IG(v/2,vλ/2)，

(12)

2.2 基于K均值聚类的多组权重因子确定方法

由ACAR等[9]提出的全局组合建模在现有的全局组合建模方法中性能表现较好，是常用组合建模方法之一。为节省计算成本，本文将其作为全局组合建模方法的代表。该方法通过优化如下最小化问题来计算权重因子：

s.t.

1Tw=1。

(13)

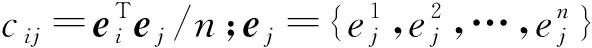
上述计算权重的方法仅有一组权重因子，可能导致某些区域的预测效果较差。为改善该问题，本文提出以K均值聚类的方法将设计空间中的样本点划分为多个不同的组，然后优化分组权重，从而获得多组权重因子。流程如图1所示，具体实现过程如下：

步骤1初始化聚类数为l0，令k=0。

步骤2利用K均值聚类将n个训练样本点划分为lk个组别。假设第q个组别所包含的样本点数为nq(j=1,…,lk)，则n=n1+n2+…+nlk。

步骤3对于步骤3所划分的组，通过最小化式(13)来获得各组权重因子，进而得到整个设计区间的权重因子。

步骤4计算测试样本点与训练样本点中各组质心的距离，以距离最近组的权重作为该聚类数下测试样本点的权重。

步骤5更新聚类数为l(k+1)，令k=k+1。重复步骤2～步骤5，直到达到最大聚类数lmax。此时优化的权重总组数为lmax(lmax+1)/2。考虑到计算成本，设置最大聚类数为10。

步骤6计算并比较不同聚类数下的测试样本点的均方根预测误差(Root Mean Square Prediction Error, RMSPE)。

步骤7以最小RMSPE所对应的聚类数作为最佳聚类数，最佳聚类数所对应的权重即为最优组合权重。

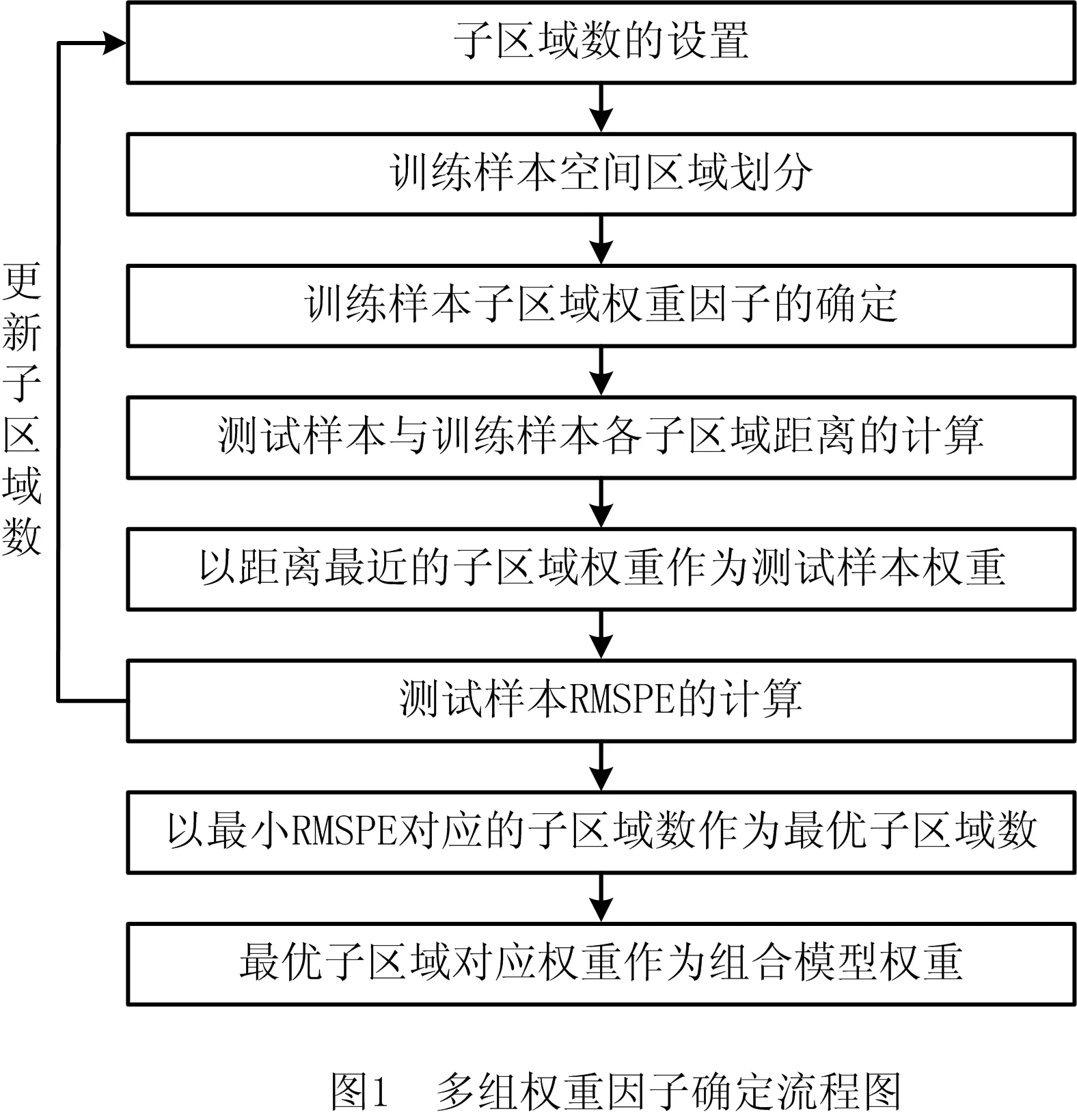
2.3 基于SSVS法和K均值聚类的Kriging组合建模

组合模型可解释为专家知识的集合，其一般形式为：

(14)

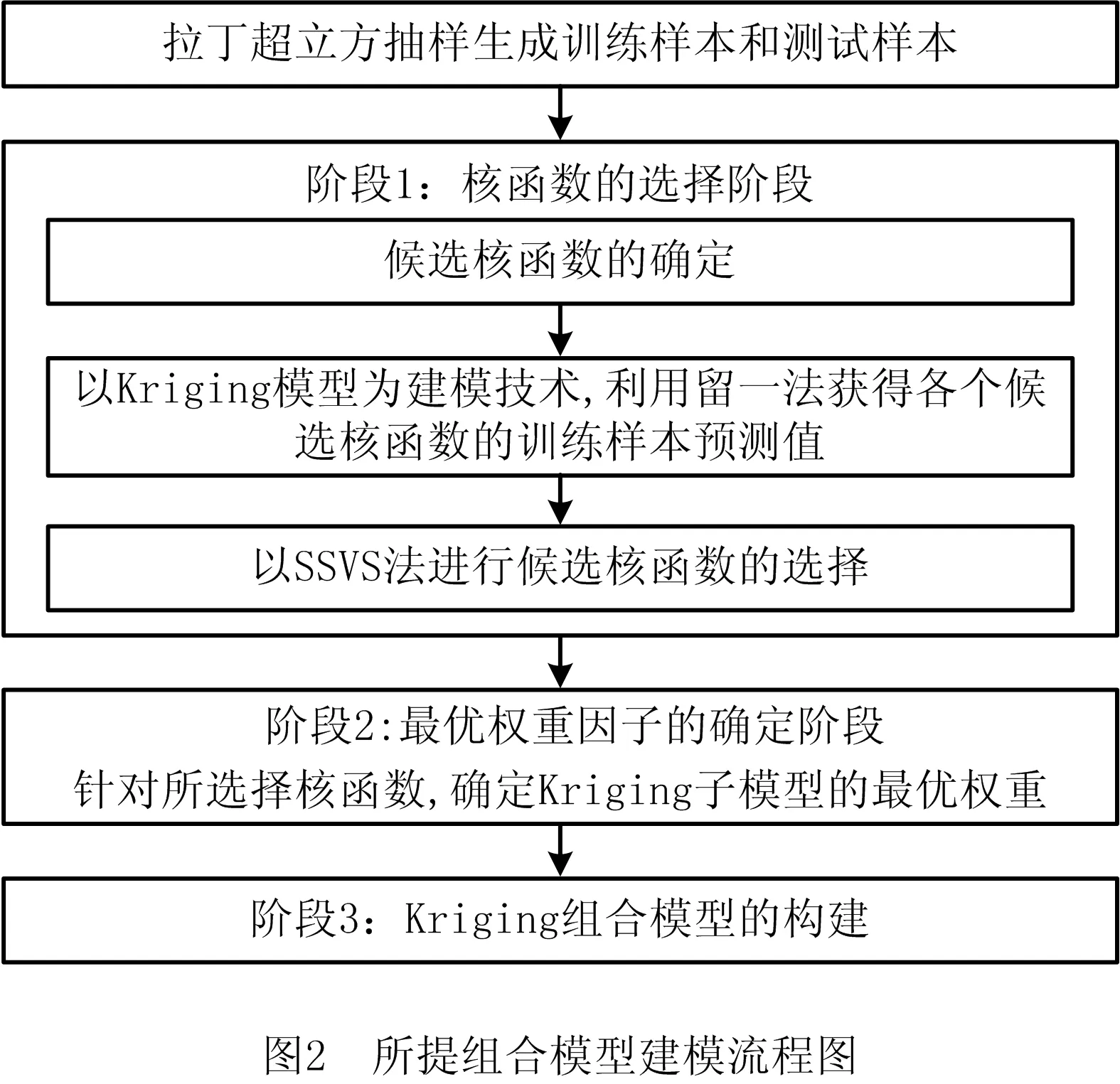
由式(14)可以看出，组合模型的两个关键因素为子模型集和权重因子。基于此，本文在Kriging组合建模过程中，同时考虑核函数的选择及多组权重因子以优化一般Kriging组合建模，其流程如图2所示，具体实现步骤如下：

步骤1利用最大最小拉丁超立方抽样产生n个训练样本点，以及Ntest个测试样本点。

阶段1：核函数的选择阶段。

步骤2选择高斯核函数、Matérn3/2核函数和Matérn5/2核函数作为Kriging代理模型的候选核函数。

步骤3在步骤1产生的训练样本的基础上，利用除第i(i=1,2,…,n)个样本点外的其他样本{(x1,y1),…,(xi-1,yi-1),(xi+1,yi+1),…,(xn,yn)}来构建单个候选核函数的Kriging代理子模型，而后利用所建立的第i个子模型来预测xi处的响应值Mj(xi)(i=1,2,…,n;j=i=1,2,…,m)。进一步，将子模型预测Mj(xi)(i=1,2,…,n;j=i=1,2,…,m)表示为式(9)的形式。

步骤4将单个核函数所构建的Kriging代理子模型看作一个变量，基于SSVS法进行核函数组合的选择。各参数的先验假设及调节参数的设置详见2.1节。

阶段2：最优权重因子的确定阶段。

步骤5利用2.2节所提方法及实现步骤，得到组合模型的最优权重因子。

阶段3：Kriging组合模型的构建阶段。

步骤6将步骤4所选择的子模型和步骤5所获得的最优权重因子代入式(14)，从而可获得本文所提Kriging组合代理模型。

3 算例研究

3.1 试验设置

为体现同类型单一核函数建模在多种场景下的不同表现性能，并证明所提Kriging组合模型在预测稳健性和预测精度方面的优越性，本文选择如下6个具有代表性的分析函数[18,21-23]：

(1)2D多模态函数

(15)

(2)Camelback函数

(16)

(3)Dette&Pepelyshev函数

(17)

(4)Hartman-3D函数

(18)

(5)Friedman函数

f(x)=10sin(πx1x2)+20(x3-0.5)2+

10x4+5x5。

(19)

(6)修正的Hartman-6D函数

(20)

其中Hartman-3D函数和修正的Hartman-6D函数中的参数ci,aij,pij分别如表1和表2所示。以上6个分析函数的试验设置如表3所示，包括维度、输入变量的定义域、训练样本的数量及测试样本的数量。

表1 Hartman-3D函数的参数设置

表2 Hartman-6D函数的参数设置

根据候选核函数的类型，本文需要建立的候选Kriging子模型包括高斯核Kriging模型、Matérn3/2核Kriging模型及Matérn5/2核Kriging模型。为方便起见，分别使用Gau、M3/2和M5/2来简单表示。全部候选Kriging子模型的线性加权是常用Kriging组合模型的一般形式，而本文所提组合建模在此基础上同时考虑了核函数的选择和多组权重因子。为证明所提方法的优越性，建立了4种不同类型的组合模型，包括既不考虑核函数选择也不考虑多组权重因子的一般Kriging组合模型、仅考虑核函数选择的Kriging组合模型、仅考虑多组权重因子的Kriging组合模型及二者同时考虑的Kriging组合模型，分别用EK、EKS、EKM、EKSM简单表示。以上7种Kriging模型中核函数的超参数θ范围均设置为[0.001,5]。

(21)

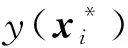
表3 各分析函数的试验设置

3.2 结果与讨论

图3所示为针对2D多模态函数、Camelback函数和Hartman-3D函数的7种Kriging建模方法的RMSPE箱线图。每个箱体的顶部和底部分别表示RMSPE的上四分位数和下四分位数，箱体中间的直线表示中位数，从箱体末端延伸的线表示剩余数据相对于下四分位数和上四分位数的延伸，最大延伸长度是四分位数范围的1.5倍，“*”符号表示超出须线限度的异常值。由图3可知：

(1)2D多模态函数中，高斯核函数在单一核Kriging模型中具有最少的异常值、最集中的数据分布和最小的平均值，说明在预测可靠性、稳健性及精度方面表现最佳，为最优核函数。同样地，通过对箱线图的分析可知，Hartman-3D函数中最优核函数为Matérn3/2核函数，Camelback函数则为Matérn5/2核函数，说明同一类型单一核函数的Kriging建模技术在不同情形下预测精度不同，没有某个单一核函数对所有的分析函数都是最优的，最优核函数高度依赖于具体问题。

(2)对比3个分析函数中组合模型与单一模型的预测性能知，无论最优单一核函数的类型如何变化，4种Kriging组合模型的箱线图须线长度、箱体大小及异常值数量均优于最差的Kriging单一模型，接近最优的Kriging单一模型，说明Kriging组合建模比单一核Kriging建模更具有普适性。

表4～表9以具体数字的形式分别展示了7种Kriging建模技术在6个分析函数不同训练样本量下的RMSPE平均值和标准差，最优值在各表中以粗体形式显示。由RMSPE平均值可知：

(1)Kriging单一模型的预测精度随核函数的变化而变化，不同核函数对应不同的RMSPE平均值。

(2)考虑核函数选择的Kriging组合模型EKS的预测精度优于未考虑核函数选择的一般Kriging组合模型EK，如Friedman函数样本量为60时，EKS的平均RMSPE为0.178 4，与EK的平均RMSPE 0.1908相比，预测精度提升了6.5%。

(3)考虑多组权重因子的Kriging组合模型EKM的预测性能优于仅考虑一组权重因子的一般Kriging组合模型EK，如Dette&Pepelyshev函数样本量为30时，EK的平均RMSPE为0.473 0，而EKM的平均RMSPE为0.402 1，精度提升了15%。

(4)同时考虑核函数选择和多组权重因子的Kriging组合建模EKSM能显著提升模型性能，在本文所列举的4种Kriging组合模型中表现最佳，如Hartman-3D函数中样本量为50时，所提Kriging组合模型的平均RMSPE为0.331 1，与一般Kriging组合模型EK相比精度提升了18.65%，与仅考虑多组权重因子的Kriging组合模型相比提升了12.71%，与仅考虑核函数选择的Kriging组合模型相比提升了3.58%。

(5)所提Kriging组合模型EKSM的预测性能在某些情况下可能优于最优的单一Kriging模型，如Camelback函数中样本量为20，说明所提组合建模技术具有较好的预测精度。由RMSPE标准差知，所提Kriging组合模型与其他3种Kriging组合模型相比，具有最大比例的最小值；与单一Kriging模型相比，小于最大值，接近最小值。说明所提建模技术具有较好的预测稳健性。

表4 2D多模态函数不同Kriging代理模型的RMSPE平均值及标准差(括号内)

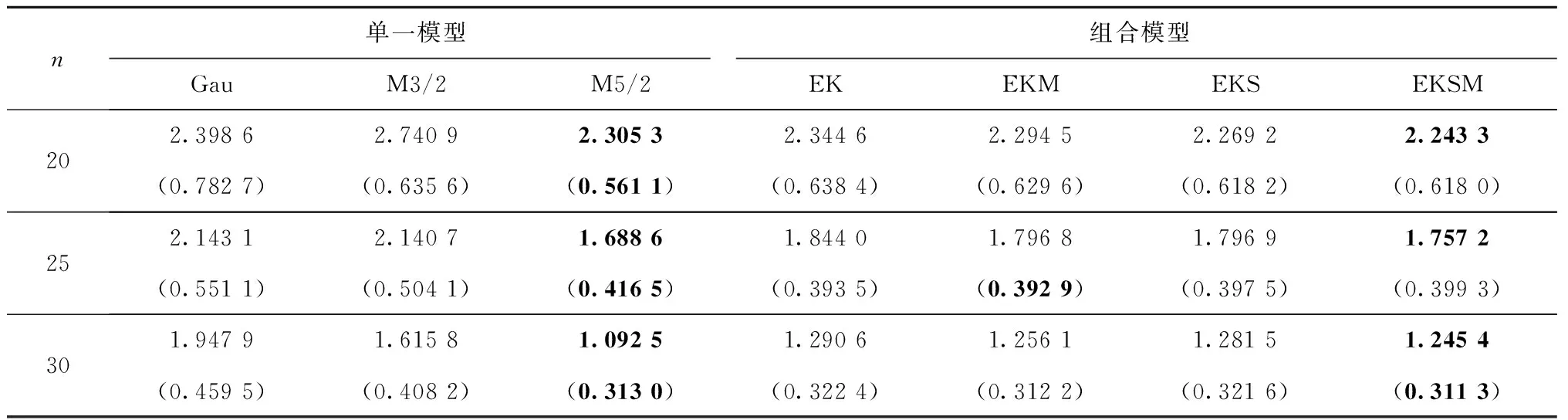
表5 Camelback函数不同Kriging代理模型的RMSPE平均值及标准差(括号内)

表6 Dette&Pepelyshev函数不同Kriging代理模型的RMSPE平均值及标准差(括号内)

续表6

表7 Hartman-3D函数不同Kriging代理模型的RMSPE平均值及标准差(括号内)

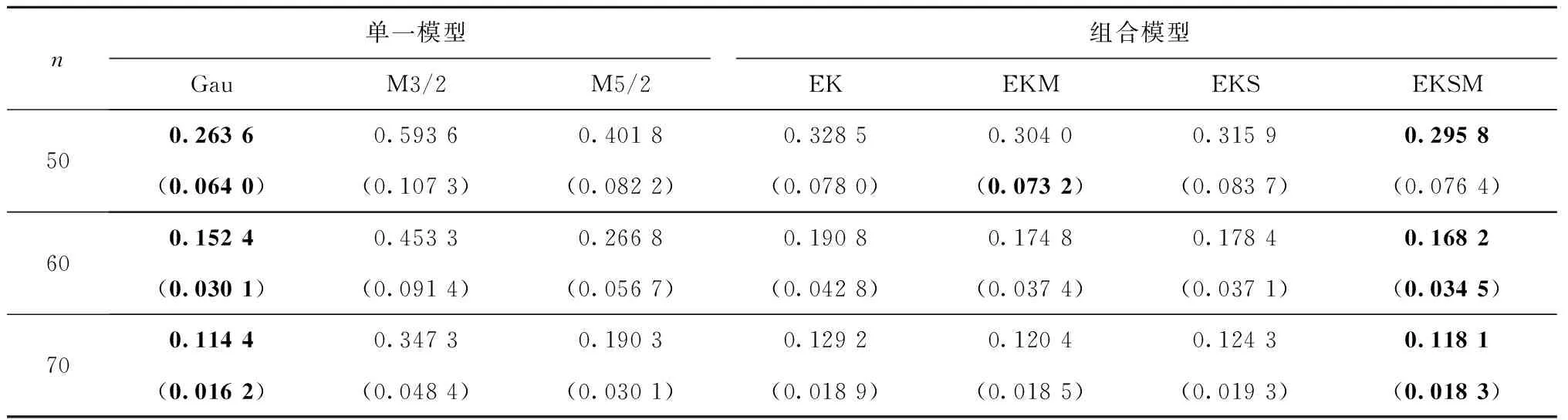
表8 Friedman函数不同Kriging代理模型的RMSPE平均值及标准差(括号内)

表9 修正的Hartman-6D函数不同Kriging代理模型的RMSPE平均值及标准差(括号内)

另外，通过分析训练样本量大小对组合模型预测性能的影响可知：①与其他3种Kriging组合模型相比，所提Kriging组合模型的RMSPE平均值和标准差在不同训练样本量下均能保持较优(最优或与最优相当)，说明所提方法的优越性受样本量的影响较小；②随着训练样本量的增加，不同Kriging模型的RMSPE平均值和标准差整体越来越小，说明训练样本量与模型预测效果整体成正比。然而，样本量的增大会增加计算成本。因此，在建模过程时应权衡试验成本和模型精度，选择合适的训练样本量。

4 实例研究

活塞运动模型模拟了活塞在气缸内的移动[24-25]，活塞的性能通过完成一个循环所需的时间来测量，即活塞轴完整旋转的循环时间Y，单位为s。通过改变活塞重量(M)，活塞表面积(S)，初始气体体积(V0)，弹簧系数(k)，大气压力(P0)，环境温度(T)和充气温度(T0)7个输入因子，可调节活塞的性能。表10列出了每个输入因子的名义值允许范围及其对应的标准差σi。由于试验过程中噪声因素的影响，输入因子的实际值与名义值并不相等，而是在名义值附近呈正态分布变化，进而导致循环时间Y的变化。优化目标是最小化Y的方差同时，使其平均值尽可能地接近0.2。输入因子和输出响应之间的影响过程可通过一系列非线性方程来表示：

(22)

其中：

(23)

(24)

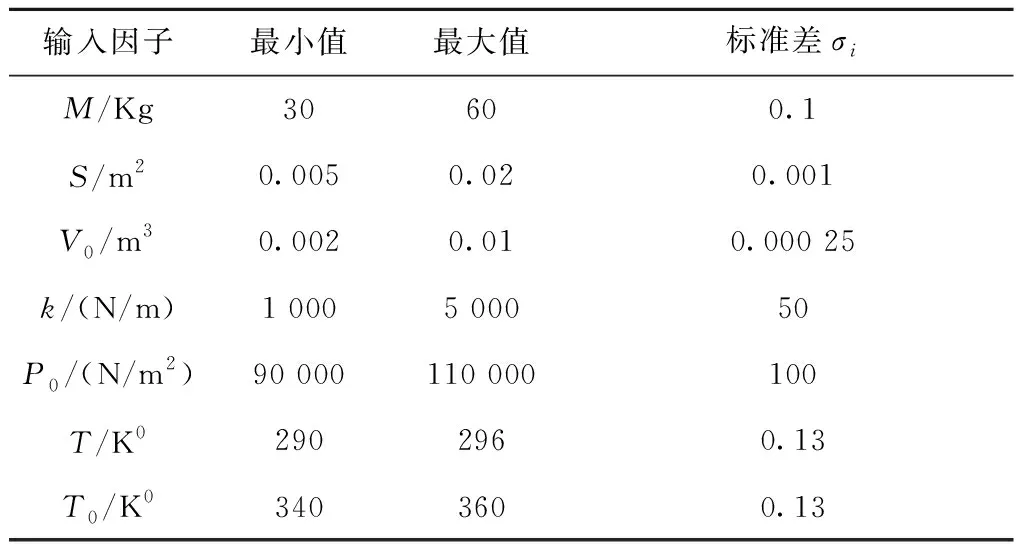
表10 活塞运动模拟中各输入因子允许的取值范围和标准差

4.1 试验设置

在质量设计中，双响应曲面优化法可同时优化均值和方差，常用于确定输入变量的最优设置。该方法首先由MYERS等[26]提出，VINING等[27]进一步将其进行普及。双响应曲面的一个关键步骤是构建均值响应和标准差响应的经验模型。为获得响应的均值和标准差，同一输入因子水平组合应重复多次试验。

在实际试验过程中，受噪声因素影响，输入因子实际值常在名义值附近随机波动。假设输入因子实际值在名义值的±3σi范围内随机变化，则噪声水平的取值范围为±3σi。相应地，本案例中的试验设计应包含两部分：①输入因子名义水平的设计;②输入因子噪声水平的设计。两部分设计均采用最大最小拉丁超立方抽样，在各自的取值范围内随机产生100个试验点。为模拟实际中同一水平组合的重复试验，噪声水平100个试验点的产生重复3次。而后将同组号输入因子的名义水平值与噪声水平值相加，即可获得相应的实际水平值。进一步地，将100组重复3次的输入因子实际水平值带入式(19)～式(21)可得到循环时间Y的值。之后对同一水平组合3次重复对应的Y值分别求平均值和标准差。

为评价所提模型的预测性能，利用Bootstrap重抽样法，分别将由试验设计获得的响应均值和响应标准差数据集以8:2随机分割为训练集与测试集，通过500次重抽样，获得500对训练集与测试集。在此基础上，每种建模方法可建立500个不同的模型并得到测试样本集的500个预测向量。然后，分别计算3种Kriging单一模型和4种Kriging组合模型在500个测试集上的RMSPE。最后，通过比较不同Kriging组合模型的RMSPE来说明所提组合模型方法的优越性。

4.2 不同方法的预测性能分析

为说明所提建模技术的有效性，图4以箱线图的形式、表11以具体数字的形式分别显示了3种Kriging单一模型和4种Kriging组合模型对于均值响应和标准差响应的RMSPE。在表11中，粗体表示对应建模技术在所使用的评价标准中表现最优。

由图4和表11对应的响应均值可知，在3种Kriging单一建模技术中，Matérn3/2核Kriging模型的离群点数量最少，RMSPE均值和标准差最小，说明其预测精度和稳健性最好。高斯核Kriging模型的预测性能最差，进一步说明在输入变量与响应之间关系未知时，若直接采用最广泛使用的高斯核函数，会造成较差的预测结果。4种Kriging组合建模技术中，所提建模技术具有最小的RMSPE均值和标准差，预测性能优于其他3种单一Kriging模型。另外，Kriging组合模型与Kriging单一模型整体相比，组合模型具有比最差单一模型较好同时与最优单一模型相当的预测效果。说明组合模型能充分利用每个单一模型的预测能力来获得更加强大的预测能力，在输入变量与响应之间关系未知时，可保证较精确和稳健的预测效果。同样地，由图4和表11对应的响应标准差可知，所提组合建模技术具有最小的RMSPE均值，说明其具有较好的预测精度；4种Kriging组合建模的标准差大小(箱线图的数据集中程度)相当，其中所提Kriging组合建模技术优于一般Kriging组合建模技术，提升了预测稳健性；所比较的7种Kriging模型中，所提方法具有相对较少数量的离群点，从而说明了其预测的可靠性。

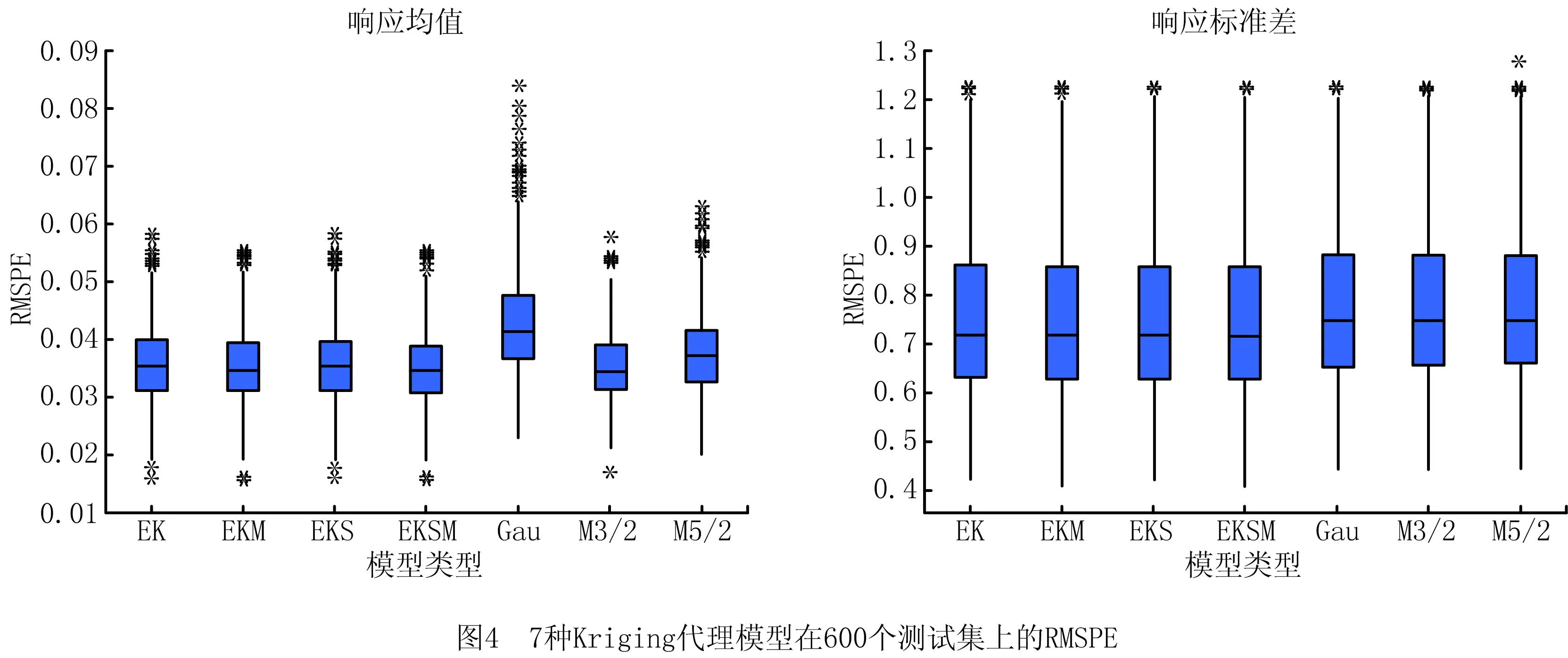
表11 7种Kriging代理模型的RMSPE平均值及标准差(括号内)

4.3 不同方法的优化结果分析

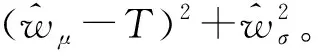
在本案例中，尽管输出响应与设计变量之间的真实关系未知，但是为了充分说明所提建模技术的优越性，假设真实模型为3类单一核Kriging模型之一，从而响应均值和响应标准差的假设真实模型组合共有9组。首先将本文所比较7种Kriging建模技术的最优参数组合分别作为9种真实模型的输入，则可获得每种建模技术的9组真实优化目标值。进一步，以欧式距离作为评价标准，计算7种Kriging建模技术与真实模型的真实优化目标值之间的距离，其结果如表12所示。表12显示了所提Kriging组合建模技术具有最小的欧氏距离均值和标准差。由均值对比可知，所提方法与最优Kriging单一建模技术相比提升了65.34%，与其他Kriging组合建模技术相比最少提升了45.5%。由标准差对比知，所提方法与最优Kriging单一建模技术相比提升了84.12%；与其他Kriging组合建模技术相比至少提升了22.7%。同时，不论真实模型的具体形式如何，Kriging组合建模技术均能获得与真实模型距离相对较小的优化结果。由此说明所提Kriging组合建模技术对模型形式的不确定是稳健的。

表12 7种Kriging代理模型与真实模型的的真实优化目标值的距离

5 结束语

本文提出一个新的Kriging组合建模方法，通过6个仿真算例和1个工业实例的对比分析发现：

(1)考虑多个核函数的Kriging组合模型通过集成多个核函数的预测性能，在多种场景下都能保持较好的预测精度，与仅考虑单个核函数的Kriging单一模型相比更具普适性和稳健性。

(2)SSVS核函数选择方法有效提升了Kriging组合模型的预测效果，与一般Kriging组合模型相比，避免了冗余问题的出现。

(3)考虑全局多组权重因子的Kriging组合模型，采用多个区域的兼顾策略，保证了局部和全局都具有较好的预测性能，优于仅考虑一组权重因子的Kriging组合模型。

本文的贡献主要在于所提建模技术不仅具有较好的预测性能，还能够得到较稳健的优化结果。与此同时，关于Kriging建模技术还得出4个有趣的发现：

(1)没有某个单一核函数在Kriging建模的所有情形中都表现最优。

(2)并不是所有的核函数都能提升Kriging组合模型的预测性能。

(3)与全局组合模型相比，设计空间的区域划分可在保证经济性的基础上，进一步提升Kriging组合模型的预测性能。

(4)来自单个建模技术的最优参数组合可能被低估或高估。

基于本文的研究内容，未来可进一步研究的方向包括：①在所提Kriging建模技术中考虑噪声变量的影响；②将所提方法拓展到多响应的情形；③考虑组合模型中子模型之间的相关性。