乌鸦搜索算法的改进及其在工程约束优化问题中的应用
汪逸晖,高 亮
(华中科技大学 机械科学与工程学院,湖北 武汉 430074)
0 引言
在工程领域,传统优化算法在解决实际问题中取得了可喜的成果。但优化问题差异性较大,范围从单目标到多目标、从连续到离散、从有约束到无约束,面对复杂的设计问题,传统优化算法存在仅能求出局部最优解、求解结果依赖于初始值等不足[1]。元启发式算法为此类问题提供了一种实用且有效的解决方案,能在可接受的运行时间内求得NP-Hard问题的最优解或近优解[2-3]。
乌鸦搜索算法(Crow Search Algorithm, CSA)是由ASKARZADEH[4]于2016年提出的一种基于乌鸦智能行为的新兴群智能元启发式算法。该算法在每次迭代中产生多个并行计算的个体,通过模拟乌鸦种群间搜寻食物的行为解决优化问题。由于CSA具有结构简单、参数少、操作灵活等特点,目前已成功应用于函数优化、特征选择等领域。ABDELAZIZ等[5]使用CSA对辐射状配电网中的导体选择问题进行了优化求解,实验结果表明CSA较传统优化算法表现更加优秀;ALEEM等[6]将CSA应用于滤波器优化设计,优化测试结果表明该算法具有快速收敛的能力,能成功解决配电网络中无共振三阶高通滤波器优化设计问题;LIU等[7]将CSA与极限学习机(Extreme Learning Machine, ELM)结合,建立了地下水水质评价模型CSA-ELM,以解决水质评价中水质模糊、水质参数不兼容等问题,测试结果表明CSA-ELM模型性能优于ELM、内梅罗指数法(Nemerow Index Method, NIM)和反向传播(Back Propagation, BP)模型,具有较高的稳定性与可靠性;MEDDEB等[8]将CSA应用于无功优化调度问题,在基准测试系统(IEEE 14-bus, IEEE 30-bus &Tunisian 86-bus)的测试中CSA表现优于对比算法,成功解决了无功优化调度问题;SATPATHY等[9]将改进的CSA应用于虚拟机放置问题,通过排队模型管理调度大量虚拟机,运用算法选择服务器并进行部署以达到优化资源和减少功耗的目的,测试结果表明改进的CSA的优化性能较同类算法表现更加优异。由于乌鸦搜索算法是基于乌鸦搜索食物的特性创建的一种群智能算法,该算法与大多数群体智能算法类似,存在搜索精度低、易陷入局部最优值和算法早熟的缺点。
为克服上述缺陷,近年来研究者们根据基本乌鸦搜索算法提出了各种改进策略。MOHAMMADI等[10]针对CSA做了两点改进:首先引入基于优先级的方法,确定了乌鸦如何选择跟踪对象,将原算法中的随机选择改为在每次迭代中从最优的乌鸦群中随机选择,从而增加乌鸦搜寻到最优解的可能性;其次提出一种用于调节有效飞行长度的方法,可根据乌鸦的接近程度确定有效飞行长度,有助于乌鸦更好地搜索,测试结果表明改进算法的收敛特性优于CSA;JAIN等[11]提出了改进的乌鸦搜索算法(Improved Crow Search Algorithm, ICSA),有效地解决了高维全局优化问题,改进算法在乌鸦位置更新机制中加入经验系数,该系数的添加可通过随机扰动在局部最优解的附近生成新解,测试结果表明,在稳定性、搜索能力和收敛速度方面ICSA优于CSA;SHI等[13]提出改进的乌鸦搜索算法,在原始CSA位置更新机制中加入自适应惯性权重,在搜索初始阶段,较大的惯性权重可以增强全局搜索能力,而在最后阶段,惯性权重减小增强了局部探索,避免了过度搜索导致的位置反复跳跃,使乌鸦可迅速移至极值点,测试结果表明改进算法的优化性能与收敛速度有明显提高;KHALILPOURAZARI等[13]将正弦余弦算法(Sine Cosine Algorithm, SCA)与CSA结合提出正弦余弦乌鸦搜索算法(Sine Cosine Crow Search Algorithm, SCCSA),该混合算法将正弦余弦局部优化算子嵌入乌鸦位置更新机制,确保所有乌鸦在更新位置时遵循当前最优解优先且不会生成质量低劣的随机解,同时乌鸦在搜索时以设定的方式移动,提高了算法的探索能力,函数测试结果表明SCCSA的优化性能优于CSA,算法的收敛图也证明SCCSA可快速收敛到最优解;ELLA等[14]提出粗糙乌鸦搜索算法(Rough Crow Search Algorithm, RCSA),将CSA与粗糙搜索机制(Rough Searching Scheme, RSS)结合,有效地解决了在搜索高维优化问题的全局最优解时可用信息不精确和粗糙等问题,在实现优化时,利用CSA搜索全局优化问题的近似解,再引入RSS来提高精度,测试结果表明,RCSA在计算精度上的表现更加优秀;QU等[15]提出一种基于非劣解集邻域搜索的乌鸦搜索算法(Non-inferior Crow Search Algorithm, NICSA),该算法通过非劣解的决定因子,使乌鸦个体在进化过程中自动选择记忆搜索模式或邻域搜索模式,通过这种策略,算法的局部搜索与全局搜索变得更加平衡,函数测试表明该算法在搜索准确性、收敛速度等方面均优于CSA。
综上所述,众多改进算法的最终目的都是为了提高算法的搜索精度和全局寻优能力,以及加快算法收敛速度。由此,本文基于乌鸦搜索算法提出了CSA的改进算法(Modified Crow Search Algorithm, MCSA),主要对CSA的参数、寻优策略和优化算子作出以下3点改进:①将动态感知概率替换原算法中的感知概率,让乌鸦在迭代初期趋向全局搜索,避免算法早熟;②引入莱维飞行策略,从而解决CSA搜索机制单一的缺点,有效地降低算法寻优的盲目性,避免其陷入局部最优;③在寻优过程中引入变异更新机制,增加了解的多样性,提高了CSA的搜索效率。将MCSA与近年提出的优化算法在标准测试函数上进行函数寻优测试,实验结果对比表明MCSA作出的改进可以提高算法求解精度、稳定性以及搜索效率。最后,为了解决面对约束优化问题时求解困难以及可能存在优化结果不符合约束的情况,将FAD(feasibility and dominance)准则与MCSA结合,构建了约束处理机制,并通过3个工程优化问题测试验证MCSA的可行性与优越性。
1 乌鸦搜索算法
1.1 基本原理
乌鸦是人类以外具有一流智商的动物,它们可以使用工具进行复杂沟通,并能回忆长达几个月的食物储藏处。乌鸦会观察同类储藏食物的地点,并在主人离开后将食物偷走。同样,乌鸦为了误导竞争者,会制造一个假的藏物点,并根据竞争者是否看到自己埋藏食物的实际情况来判断竞争者的行为。最后,它们综合各种信息后决策应该采取何种方式藏匿或取回食物[16-17]。

假设迭代中乌鸦j想要去它的藏物点mj,iter,同时乌鸦i决定跟踪乌鸦j并接近其藏物点。此时,可能会发生如下两种状态:状态一,乌鸦j不知道乌鸦i跟踪它,乌鸦i将接近乌鸦j的藏物点;状态二,乌鸦j发现被乌鸦i跟踪,为了保护自己的藏物点不被偷窃,乌鸦j飞到搜索空间内的随机位置以欺骗乌鸦i。
状态一和状态二总结如下:
xi,iter+1=
(1)
式中:rj为在(0,1)区间均匀分布的随机数;fl为飞行长度;AP为感知概率。
1.2 优化步骤
乌鸦搜索算法流程图如图1所示。

算法具体步骤如下:
步骤1初始化乌鸦群,包括定义优化问题的参数和约束,然后设定种群数量(N)、最大迭代次数(itermax)、飞行长度(fl)与感知概率(AP)。
步骤2初始化乌鸦的位置和记忆,定义N只乌鸦随机分布在搜索空间内,每只乌鸦代表一个候选解,最初迭代中乌鸦将食物隐藏在初始位置。
步骤3评估适应度值,计算每个乌鸦个体的适应度函数,通过比较适应度值的大小来确定其位置质量的好坏。
步骤4生成新的位置,乌鸦i随机选择跟踪种群内的一只乌鸦j并获得其藏物点(mj),乌鸦i的位置更新由式(1)得出,该过程适用全体乌鸦。
步骤5检查新位置的可行性(如是否越界),如新位置符合要求,乌鸦会更新它的位置,否则,乌鸦则停留在当前位置。
步骤6评估新位置的适应度函数,计算每个乌鸦新位置的适应度函数值。
步骤7更新记忆,乌鸦按如下公式更新记忆;
(2)
步骤8检查终止条件,重复步骤4~步骤7,直至达到最大迭代次数。当满足终止标准时,将目标函数的最佳藏物点位置作为优化问题的最优解。
2 CSA与其他智能优化算法的比较
在实现优化时,飞行长度(fl)与感知概率(AP)设为固定值。飞行长度的取值可影响算法的搜索能力(如图2),乌鸦i可在虚线任意位置飞行。fl过小,算法易陷入局部最优;fl过大会使算法趋向全局搜索,但算法收敛性变差。感知概率可控制算法的集中性与多样性,其决定了乌鸦由状态一或状态二更新位置。AP越小,乌鸦更趋向于选择局部搜索,收敛速度会提高但易陷入局部最优;AP越大,乌鸦更趋向于随机搜索,减少了乌鸦停滞在局部最优点的可能性,但收敛速度会降低。参数设置是优化算法的缺点之一,因为它是一项耗时的工作。元启发式算法的性能优化取决于对参数的适当调整,使得解的品质依赖于参数的选取。除去种群数量与最大迭代次数,一些著名的智能优化算法,如遗传算法的设置参数为选择方法、交叉方法、交叉概率、变异方法、变异概率和替换方法(6个);粒子群算法的设定参数为权重惯量、最大速度、个体学习因子和社会学习因子(4个);和声搜索算法的设定参数为记忆库取值概率、微调概率和音调微调带宽(3个)。较多的参数在编程实现上较为复杂,参数的设定大部分依靠经验,想要得到较精确的解需要大量的训练时间。乌鸦搜索算法结构简单,参数设定为飞行长度与感知概率(2个),相较而言更容易实现优化。

CSA为非贪婪算法,如果乌鸦生成的新位置不优于其当前位置,它仍会移动到新位置(乌鸦更新位置点xi,藏物点mi保持不变)。与其他算法相比,非贪婪算法的优点在于可增加种群的多样性,同样CSA包含可以存储优质解的存储器,每次迭代中每只乌鸦都会随机选择一只乌鸦(可能是乌鸦本身)并向其藏物点位置(该乌鸦目前找到的最优解)移动,这意味着在CSA的每次迭代中,目前所找到的最优解将直接用于寻找更优解。
3 改进的乌鸦搜索算法(MCSA)
本节主要从3个方面对标准CSA算法进行改进:①采用动态感知概率替代原有的固定感知概率,使算法在搜索初期更趋向于全局搜索,避免算法早熟;②引入莱维飞行策略替代原算法中的随机飞行,避免了乌鸦在无领导者的情况下盲目飞行;③由遗传算法中变异思想启发,在算法寻优过程中引入变异机制,以增强乌鸦种群的多样性以及搜索效率。
3.1 动态感知概率
在标准CSA中,乌鸦的位置更新策略由式(1)可知,感知概率AP的设定大小可影响乌鸦选择何种搜索方式,较小的感知概率会使乌鸦的跟踪行为更不易被其他乌鸦发现,推动其向最佳藏物点逼近,从而促使种群集约化和算法收敛,即乌鸦更趋向于局部搜索;反之,乌鸦将以较大概率在搜索空间中随机飞行,以促使种群的多样性,即全局搜索。可以看出,感知概率在优化过程中保持不变并不利于算法在迭代初期保持较高的种群多样性以及在后期保持较好的收敛能力。因此,引入动态感知概率,较大的感知概率在搜索初始阶段可增强全局搜索能力,并且感知概率在迭代的最后阶段减小,可增强算法局部搜索能力,算法可迅速收敛至极值点。动态感知概率满足凸型递减曲线(Convex Descending Form,CvDF)形状,可使AP在迭代初期保持一个相对较大的初值,随着迭代次数的增加而趋于减小,直至到达最大迭代次数,其表达式为:
(3)
式中:iter为当前迭代数;itermax为最大迭代次数;APmax为最大感知概率。
3.2 莱维飞行搜索策略
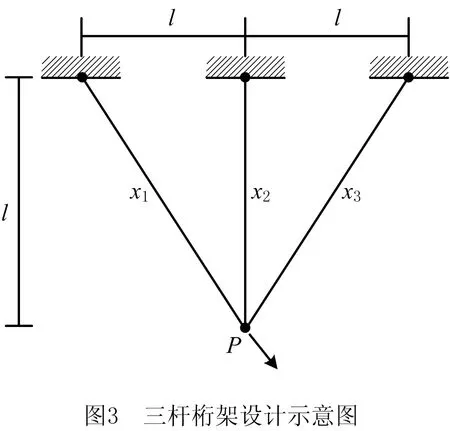
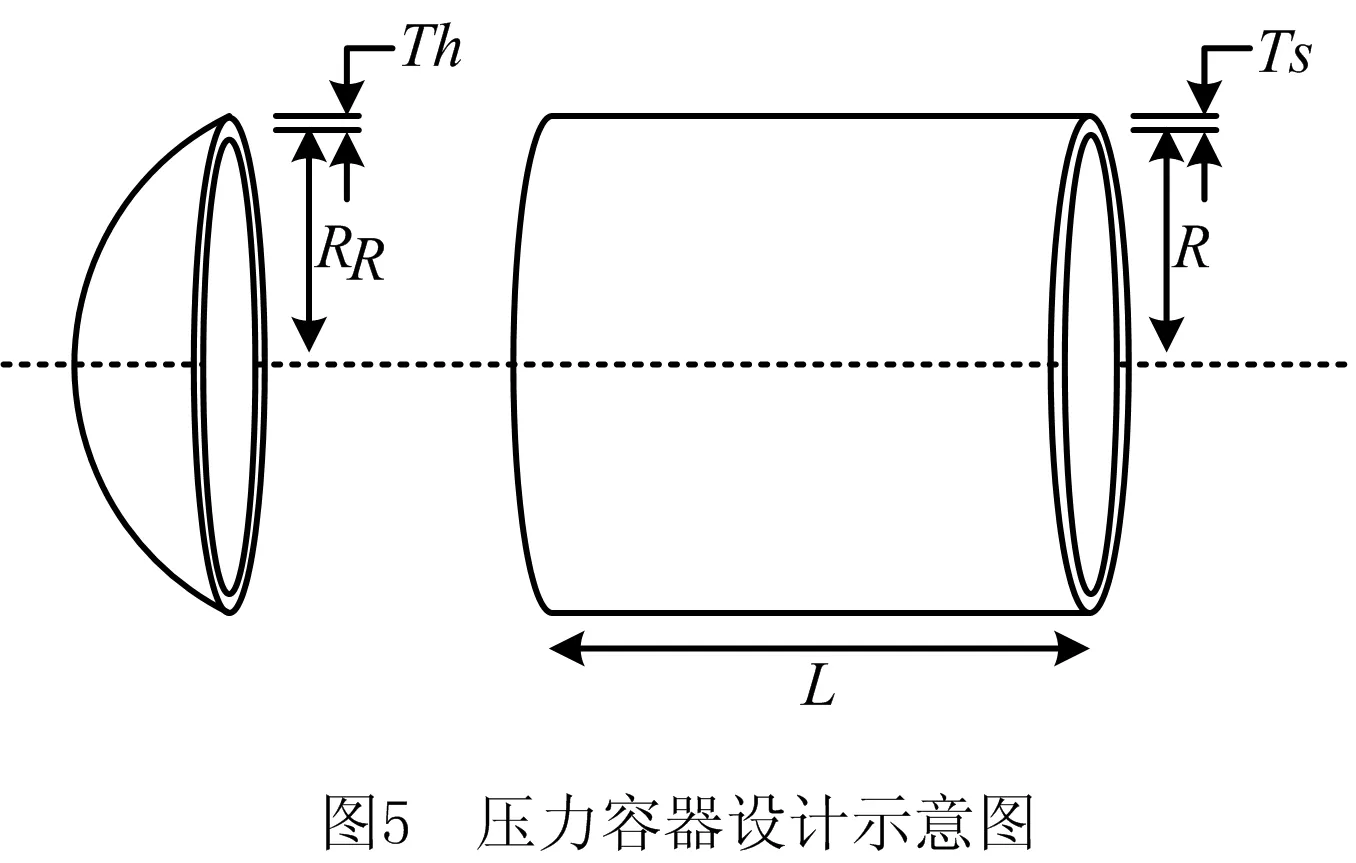
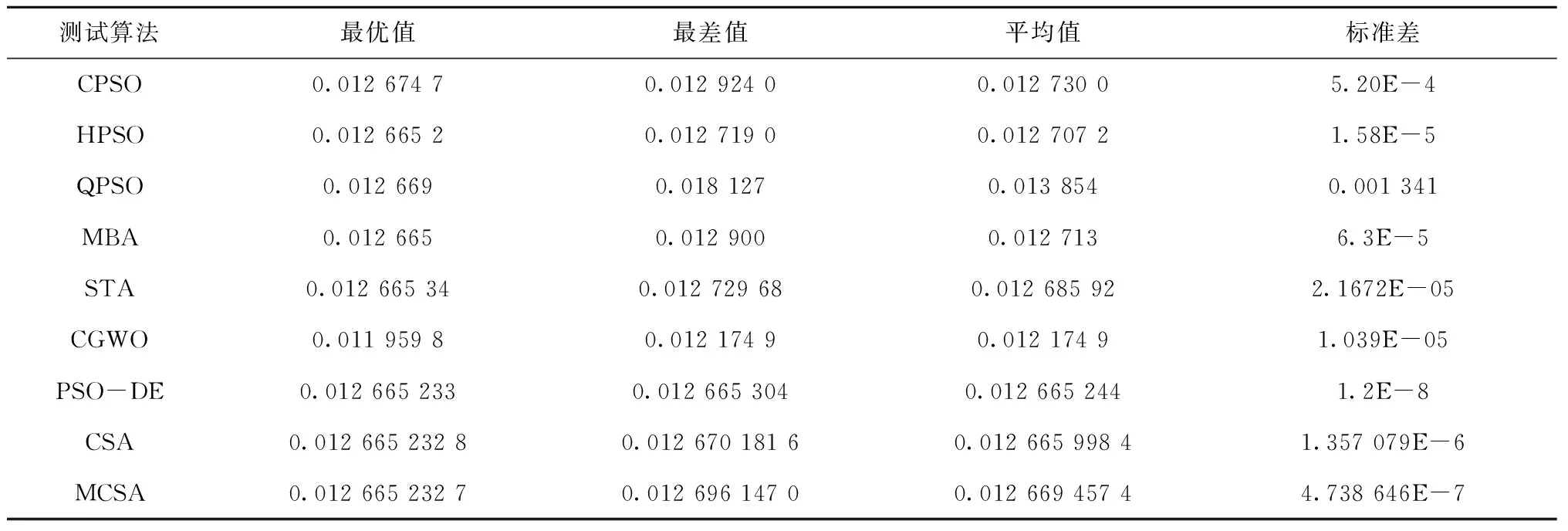
在标准CSA中,由式(1)可知,乌鸦在状态二(r xi,iter+1= (4) (5) (6) 其中:ri,rj,ra均为(0,1)区间内均匀分布的随机数;γ,σ均服从标准的正态分布;n为优化问题维度;Г(x)=(x-1)!;a为步长缩放因子,用于控制随机搜索的范围;β为常数,取值范围在[1,2]之间,为便于计算,本文采用文献[25]中参数计算莱维随机数(a=0.01,β=1.5)。 标准CSA算法随机产生初始种群,初始解的产生具有很大的随机性,若想要获得质量较高的初始种群须增加种群规模,但计算量也会随之增加,不利于算法寻优。因此,MCSA在算法迭代过程中引入变异更新机制可增加种群的多样性,提高个体质量,同时可使陷入局部最优的个体通过变异跳出局部最优以增加算法的搜索效率。在每次迭代中,选择当前质量最优的个体在更新记忆前进行变异操作,且步长随迭代次数增加而逐步减小,在迭代初期保证了陷入局部最优的个体得到较大幅度的变异,从而重新获得搜索能力,变异幅度在迭代后期也相对减小,避免了过多的变异行为干扰其搜索行为,从而保持搜索的连贯性。同时,为保证变异机制朝着有利方向进行,在变异之后,比较变异前后个体的适应度函数值,将保留较优的个体作为当前最优解,以此实现有效变异操作。变异更新机制的加入,既能保证算法在迭代初期种群的多样性,避免陷入局部最优,同时确保算法在迭代后期时拥有较强的收敛能力。变异更新机制如下: (7) (8) MCSA算法的伪代码如下: 输入:目标函数,种群数量N,最大迭代次数 输出:当前全局最优解 1: 初始化乌鸦位置; 2: 初始化乌鸦记忆 3: 计算乌鸦的适应度值 4: while终止条件不满足 5: for i=1:N 6: 随机跟踪一只乌鸦 7: 计算感知概率 8: if r≥AP 9: xi,iter+1=xi,iter+ri×fl×(mj,iter-xi,iter) 10: else 11: xi,iter+1=xi,iter×(1+Levy(n)) 12: end if 13: end for 14: 检查新位置的可行性 15: 根据公式(7)(8)产生变异新位置 16: 评估新位置的适应度函数 17: 更新记忆 18: end while 本文选取近年发表的优化算法作为对比算法:SPO(stochastic paint optimizer)[19],HGSA(hyperbolic gravitational search algorithm)[20],FDO(fitness dependent optimizer)[21],LPB(learner performance based behavior algorithm)[22],ROA(root based optimization algorithm)[23],DA(dragonfly algorithm)[24],CSA(crow search algorithm)。所有算法的测试环境为:Windows 10,Intel(R)Core(TM)i7-6700 HQ CPU,主频3.0 GHZ和内部存储器16 GB,编程工具为MATLAB 2018b。所有算法均独立运行30次,种群规模N=30,最大迭代次数设置为1 000,其他主要参数设置如表1所示。 表1 算法主要参数的设置 本文对多个不同特点的标准测试函数进行函数寻优测试,标准测试函数及其具体信息如表2所示。同时选取包含10个CEC Benchmark函数作为额外的测试评估,其基本信息如表3所示。为了验证MCSA算法的高效性,将算法的终止条件设定为CPU计算时间(5 s,10 s和20 s),并使用相对百分比增加(Relative Percentage Increase, RPI)来评价算法性能。其中使用了对比算法独立运行30次的平均目标函数值来计算RPI,即: (9) 式中:fC为对比算法C独立运行30次的平均目标函数值;C为SPO、FDO、HGSA、CSA和MCSA;fbest为对比算法中的最优值。 表2 标准测试函数 表3 CEC-C06 2019测试函数 另外,为探究参数设置对MCSA算法性能的影响,选取了两个单峰函数与一个多峰函数(F1、F5、CEC05)作为测试函数,对MCSA的控制参数(fl和APmax)进行了研究,将fl设定为4个独立的值(0.1,1,2,4),APmax设定为3个独立的值(0.1,0.5,0.8),其他参数保持不变的情况下求解最优值。 如表4与表5所示为不同算法在测试函数上运行结果,其中Mean表示寻优平均值,Std.表示标准差。由表4可以看出,对于F1和F2,MCSA与SPO表现最佳,可直接搜寻到最优解;对于4个测试函数(F5,F7,F9,F10),MCSA的优化性能最强,明显优于其他算法;对于F3和F4,MCSA的寻优结果仅次于HGSA。在CEC2019函数测试结果中,对CEC01、CEC2、CEC3和CEC10,MCSA的寻优精度皆优于其他算法;对CEC05,MCSA的寻优结果仅次于HGSA;对CEC09,MCSA的寻优结果仅次于FDO。 表4 标准测试函数实验结果 表5 CEC-C06 2019测试函数实验结果 续表5 如表6所示为在CPU时间为5 s的情况下,MCSA的平均RPI为2.09%,优于SPO、FDO、HGSA、CSA,而SPO、FDO、HGSA、CSA的平均RPI分别为3.10%、3.36%、2.21%、10.14%。表7给出了CPU时间为10 s和20 s的情况下5种对比算法的平均RPI,由表7可以看出,MCSA的平均RPI为1.91%,而SPO、FDO、HGSA、CSA的平均RPI分别为2.26%、2.78%、2.05%、9.43%,MCSA仍为最优。总的来说,算法测试结果表明MCSA在搜索精度、稳定性和搜索效率方面表现优秀。 表6 CPU=5 s下的算法RPI对比结果 续表6 表7 CPU=10 s和20 s下的算法RPI对比结果 如前所述,参数设置对于MCSA算法性能的影响显著。表8展示了当fl取值分别为0.1、1、2、4,APmax取值分别为0.1、0.5、0.8时测试函数的寻优结果。由表8可知,fl和APmax的取值会影响算法的稳定性与搜索精度,当fl=2,APmax=0.5时,MCSA在3个测试函数中取得的结果最优,较小的飞行长度和感知概率会使算法陷入局部最优,降低算法的搜索精度与稳定性。在面对不同优化问题时,可对算法参数进行微调以达到最优的结果。 表8 MCSA控制参数对算法性能的影响 续表8 约束优化问题在工程应用领域属于一类常见的数学规划问题,由于比较难求解,同时在各领域中有着广泛的应用,对此类问题进行研究具有重要的实际意义。约束优化问题的统一数学模型如下: minf(x)。 s.t. gi(x)≤0,i=1,2,…,m; hj(x)=0,j=1,2,…,q; x∈X。 (10) 其中:f,gi,hj表示在Rn中定义的实值函数;X为Rn的子集,通常包含变量上下界;gi(x)≤0为不等式约束;hj(x)=0为等式约束。 X是约束优化问题的整个搜索空间,若所求解满足约束条件,则称该解为可行解,否则称之为不可行解。约束优化问题的难点在于:约束使搜索空间不可行域的分布增加[25],而这些不可行域的分布使得在寻优过程中必须平衡约束与优化这两个方面。 由于约束的存在导致约束优化问题求解困难,本文引入FAD(feasibility and dominance)准则构建一种约束处理机制,该准则由DEB[26]提出,通常被用来选择可行解,以及在不可行解中选择相对较好的解。在比较乌鸦个体优劣时,由原先的只比较适应度函数值f(X)改为同时考虑约束违反值CV(constraint violation),该值用来定量描述一个解违反约束条件的程度。对于一个可行解,其CV值为0;对于不可行解,其CV值则大于0,计算公式如下: (11) 式中:gi(X)为不等式约束;Zhj(X)为等式约束。 算法迭代过程中采用以下准则比较个体: (1)两个个体均为可行解,选择适应度值小的个体; (2)一个为可行解,另一个为不可行解,选可行解; (3)两个个体均是不可行解,选择其中违反约束程度小的个体。 该准则公式概括为: (f(X1),CV(X1))<(f(X2),CV(X2)) ⟺ (12) 针对约束优化问题结合MCSA算法,构建了约束处理机制,以提高算法在约束优化问题中的性能。以下通过3个工程约束优化实例验证MCSA的有效性和优越性。 5.3.1 三杆桁架设计问题 三杆桁架设计问题的目的是通过调整横截面积(x1和x2)来最小化三杆桁架的体积。该三杆式桁架在每个桁架构件上受到应力(σ)约束,如图3所示。该优化问题具有一个非线性适应度函数、3个非线性不等式约束和两个连续决策变量,如下所示: s.t. 0≤xi≤1,i=1,2; l=100 cm,P=2 kN/cm2,σ=2 kN/cm2。 (13) 如表9所示为MCSA在30次独立运行中针对三杆桁架设计问题获得的最佳解决方案。获得的统计结果与NCCO[27](neighborhood-based consensus for continuous optimization)、SCA[28](sine cosine algorithm)、SC[29](society and civilization algorithm)、PSO-DE[30](hybridizing PSO with differential evolution)、DSSMDE[31](dynamic stochastic selection with multimember differential evolution)、MBA[32](mine blast algorithm)、WCA[33](water cycle algorithm)和CSA进行比较,测试结果如表10所示。与其他算法相比,MCSA在求解三杆桁架设计问题上获得了不错的结果。就最优解而言,MCSA的优化效果要优于SC、SCA、NCCO和MBA;MCSA的平均求解精度优于CS、MBA、SCA、NCCO与WCA;标准差最小也证明了MCSA具有较好的稳定性。 表9 MCSA在三杆桁架设计问题最优解 参数参数值x10.788 675 130 760 503x20.408 248 301 308 930g1-6.661 338 147 750 939E-16g2-1.464 101 602 808 951g3-0.535 898 397 191 049f(x)263.895 843 376 468 3 表10 不同算法在三杆桁架设计问题测试结果比较 如图4所示为MCSA求解三杆桁架设计问题的收敛曲线,可以看出MCSA具有不错的收敛速度,可在50次左右迭代后开始收敛。 5.3.2 压力容器设计问题 在该设计问题中,目标函数为压力容器的总成本,包括材料、成形和焊接成本。如图5所示,该优化问题包括4个决策变量:容器壁的厚度(x1或Ts)、半球头部的厚度(x2或Th)、内半径(x3或R)和圆柱截面的长度(x4或L)。在4个决策变量中,x1和x2为离散变量(0.062 5 in的整数倍),x3和x4为连续变量。 其数学模型表示公式如下: s.t. g1(x)=-x1+0.019 3x3≤0; g2(x)=-x2+0.009 54x3≤0; g4(x)=x4-240≤0; 0≤xi≤100,i=1,2; 10≤xi≤200,i=3,4。 (14) 如表11所示为MCSA在30次独立运行中针对该问题上求解最优值,可以看出x1和x2是0.062 5的整数倍,且x3和x4在约束范围内。如表12所示为通过MCSA获得的结果与下列算法的比较:STA[34](state tansition algorithm)、CGWO[35](chaotic grey wolf optimization algorithm)、DGA[36](GA through the use of dominance-based tournament selection)、CPSO[37](revolutionary PSO)、HPSO[38](hybrid PSO)、PSO、G-QPSO[39](QPSO combined with mutation operator)、CSA。 表11 MCSA在压力容器设计问题最优解 表12 不同算法在压力容器设计问题测试结果比较 可以看出,就最优值而言,MCSA的表现优于DGA、CPSO、QPSO、CGWO、STA和PSO,与HPSO和CSA获得的结果相同,但MCSA在平均值与标准差上均优于CSA。如图6所示,MCSA在迭代100次左右便开始收敛。 5.3.3 拉压弹簧设计问题 如图7所示,拉压弹簧设计问题的目的是在满足最小挠度、震动频率和剪应力的约束下,最小化拉压弹簧的重量。该问题由3个连续的决策变量组成,即弹簧线圈直径(d或x1)、弹簧簧圈直径(D或x2)和绕线圈数(P或x3)。数学模型表示公式如下: s.t. 0.05≤x1≤2,0.25≤x2≤1.3,2≤x3≤15。 (14) 如表13所示为MCSA在30次独立运行中针对此设计问题的最优解和约束值。如表14所示为MCSA的计算结果与STA、CGWO、CPSO、HPSO、QPSO、MBA、PSO-DE、CSA算法的比较。MCSA在最优值方面的表现仅次于CGWO;MCSA平均值优于除PSO-DE、CGWO和CSA之外的所有其他算法;对于标准差而言,MCSA仅次于PSO-DE,也说明了其具有较好的鲁棒性。如图8所示为收敛曲线也证明了MCSA可以快速找到拉伸/压缩弹簧设计问题的最佳解决方案。 表13 MCSA在压力容器设计问题的最优解 表14 不同算法在拉压弹簧设计问题测试结果比较 本文基于乌鸦搜索算法提出了改进算法(MCSA),该算法引入动态感知概率、莱维飞行策略以及变异更新机制,改进了标准CSA的参数与位置更新机制,以提高每个乌鸦个体的搜索效率,改善优化性能,并使算法在迭代过程中避免陷入局部最优。针对约束问题建立了约束处理机制,将改进算法成功运用于工程约束优化问题。乌鸦搜索算法作为近年提出的新兴算法,大部分研究成果只是基于实验数据分析与仿真阶段,对于算法的研究与应用尚有不足,未来可以从如下几个方面展开工作:①从算法本身的收敛机理、参数设定和位置更新机制等方面出发,对算法进行改进以提高算法优化性能;②利用CSA结构简单的特性,将CSA与其他优化方法混合,改善CSA存在的寻优精度与收敛性等问题;③可结合优化问题的特性对CSA进行改进与深化,以增加算法解决复杂函数的能力。3.3 变异更新机制

3.4 MCSA算法流程
4 算法测试
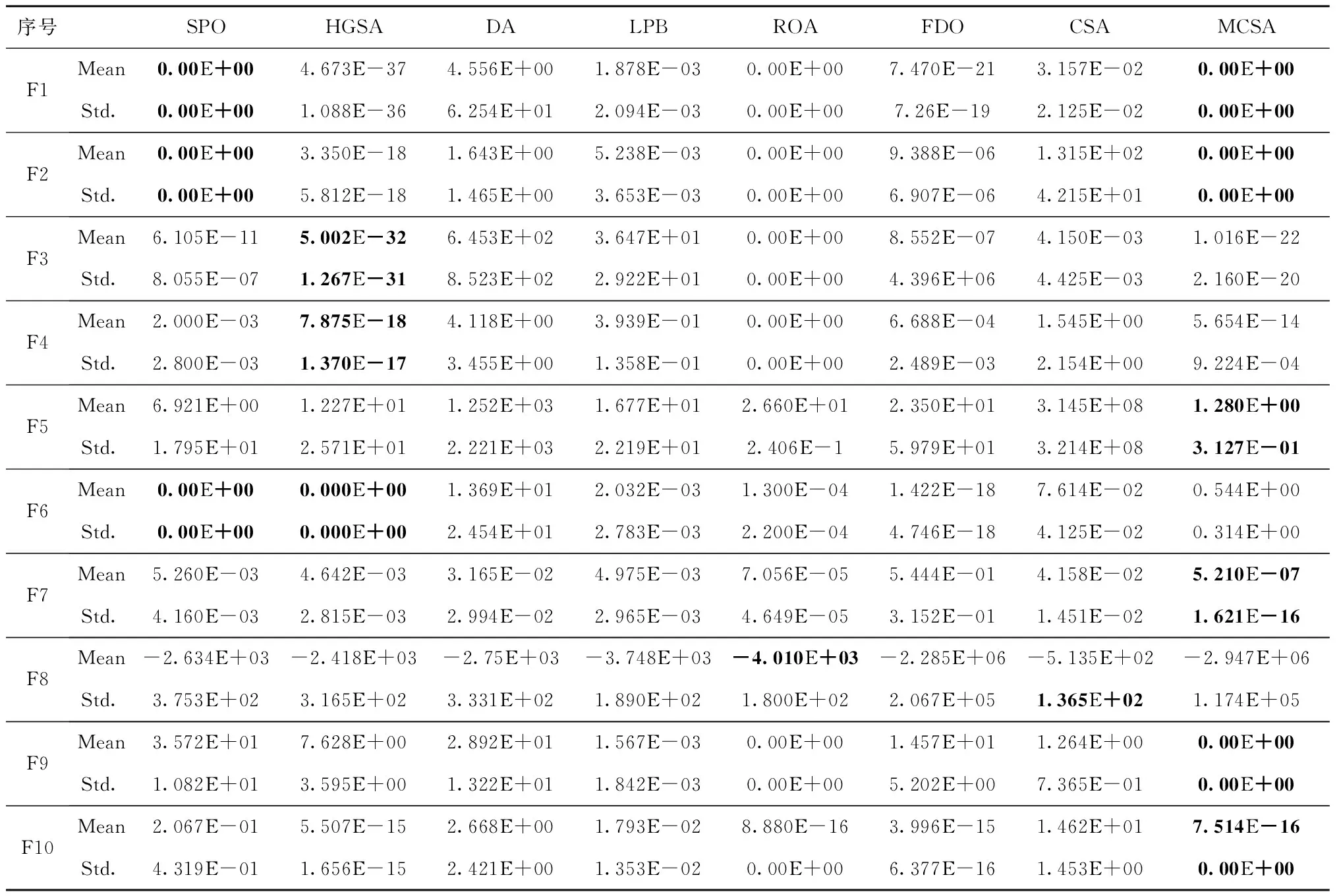
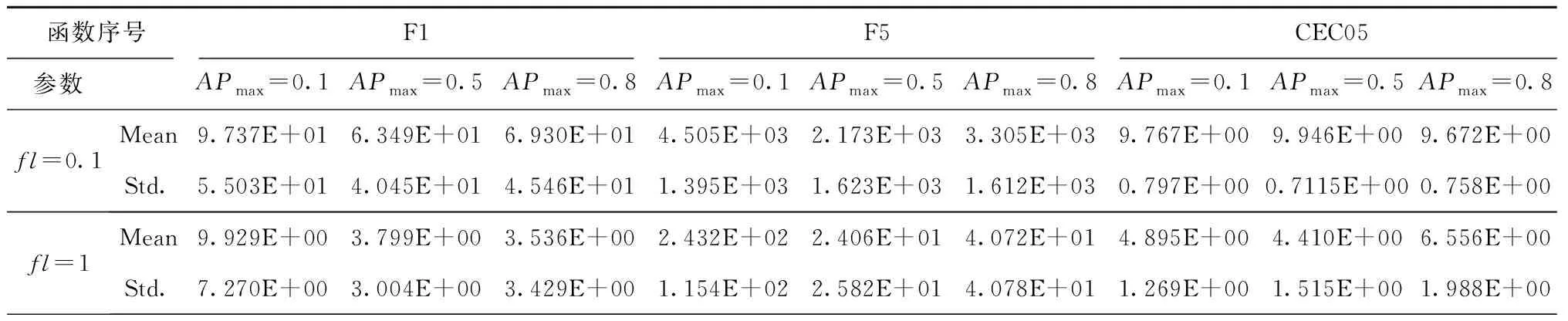
4.1 参数设置

4.2 算法测试说明


4.3 实验结果与分析






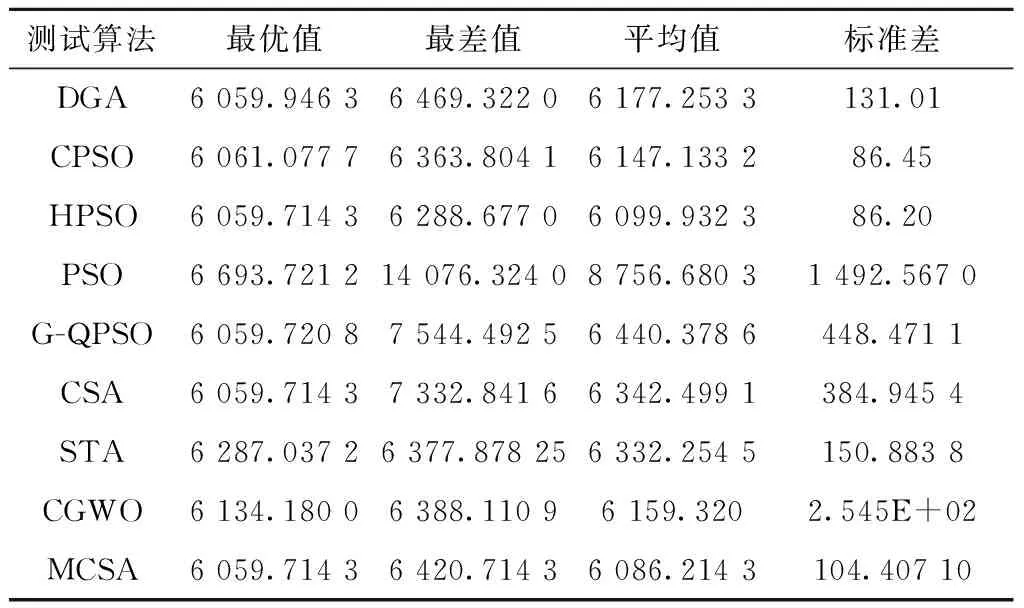
5 MCSA在工程约束优化问题中的应用
5.1 约束优化问题
5.2 约束处理机制
5.3 工程应用实例








6 结束语

