基于贝叶斯序列分割的高维时间序列在线分类算法

尹 君 张建业 李德高 景 康 周 平

1(国家电网新疆电力有限公司乌鲁木齐供电公司 新疆 乌鲁木齐 830000)2(国家电网新疆电力有限公司 新疆 乌鲁木齐 830002)3(新疆信息产业有限责任公司 新疆 乌鲁木齐 830026)

0 引 言

时间序列数据现已成为许多行业和工程领域中一种重要的数据形式，对时间序列进行在线挖掘分析具有极大的价值[1]。时间序列之间往往为非对齐的形式，所以基于欧氏距离的传统分类算法无法实现理想的效果。研究人员提出动态时间规整(Dynamic Time Warping,DTW)算法[2]解决不对准的时间序列相似性度量问题，但基于DTW的相似性度量无法度量时间序列串联结构的阶段间差异。文献[3]针对该问题提出了重要的shapelet方法，并得到了广泛的关注和应用，也实现了很高的分类精度，但shapelet类的方法存在时间复杂度高的问题。虽然许多研究人员设计了shapelet的加速算法[4-5]，但是时间复杂度依然较高。

基于概率密度的方法[6]是另一种有效的时间序列分类算法，其时间复杂度较低，能够实现在线的时间序列分类。此类方法[7]使用密度估计算法评估时间序列之间的相似性，实现快速的在线分类处理。密度估计的准确性是此类时间序列分类算法的关键部分，核密度估计(Kernel Density Estimation,KDE)[8]是最为常用的一种方法，但该方法无法应用于高维数据，而其他的非参数化密度估计方法[9]对高维数据的时间效率较低，难以满足在线密度估计的要求。

动态时间规整解决了时间序列的不对准问题，对低维度数据流的效果较好，但是高维时间序列包含丰富的时空信息，动态时间规整则忽略了这些时空信息。本文将高维时间序列投影至重建相位空间，保留高维时间序列的时空信息，然后在重建相位空间完成密度估计和相似性度量，以期提高高维时间序列的分类准确率。此外，近期一些研究人员将贝叶斯序列分割技术应用于高维数据的密度估计问题，证明该技术对于高维数据的计算效率较高。受此启发，本文将贝叶斯序列分割技术应用于时间序列的在线密度估计模型，以期对高维时间序列进行快速、准确的密度估计。

1 基于贝叶斯序列分割的密度估计

1.1 重建相位空间

如果重建空间和原空间的动态拓扑相同，那么该空间称为重建相位空间(Reconstructed Phase Space,RPS)[10]。本文采用时间延迟嵌入方法将时间序列观察投影到RPS，给定一个时间序列xm(m=1,2,…,N)，将xm投影到RPS的结果为：

xn=[xnxn+τxn+2τ…xn+(d-2)τxn+(d-1)τ]

(1)

式中:n=1,2,…,(N-(d-1)τ)，d为嵌入维度，τ为时间延迟。xn的完整时间序列可表示为：

(2)

式中:矩阵X的一行(向量)表示相位空间的一个点xn。

时间延迟嵌入方法采用滑动窗口访问时间序列的数据，嵌入维度d对应窗口的大小，时间延迟参数τ决定了下一次采样的步长。采用假近邻法调节参数d，采用最小互信息法调节参数τ。假近邻法把在d+1维空间距离远，但在d维空间的近邻点定义为假近邻，选择假近邻的时间长度低于阈值的维度作为参数d的值。

使用最小互信息函数调节时间延迟参数τ，互信息函数定义为：

(3)

式中：p(·)为概率分布函数。

式(3)评估了两个窗口Xt和Xt+τ之间的依赖性，即量化了Xt和Xt+τ之间的共享信息量。最小互信息函数的思想是选择第一次出现两个窗口互信息最小化的τ值，此时滑动窗口之间的依赖性最小。

1.2 贝叶斯序列分割

贝叶斯序列分割方法建立一个多维的直方图，再不断地对样本空间进行二分类处理。给定一个由N个样本构成的D维数据集X，将样本空间逐渐分割为若干子区域。在经过若干次的分割处理之后，每个子区域的密度可粗略计算为该子区域的数据点数量和总数据点的比例。每次分割序列，尝试M种不同的分割方式，由此可提高密度估计的准确率。

考虑一个二维的样本空间。第一次分割(j=1)产生两个子区域，后续的分割方案(j>1)记为gj={cut2,cut3,…,cutj-1}，样本空间共有j-1个子区域，设子区域p的空间体积为vp，数据点数量为np。第j次分割共有(j-1)×D种可能的分割方式，基于一个概率函数随机选择一种分割方式。分割的结束条件为获得了最优的分割结果，或者达到预设的最多分割次数。假设经过t次分割获得了最优的分割结果，子区域1≤p≤t的概率密度计算为np/(Nvp)。

在实际应用中，很难预知数据的实际密度，为了解决该问题，原贝叶斯序列分割算法定义了分区的评分指标。设一个分区为p，p含有j个子区域，分区的评分方法为：

(4)

式中:nk为子区域k的数据量;Vk为区域的体积;参数α和β为常量;D(·)为狄利克雷分布，其参数为(α,α,…,α)，D(·)作为分区的后验分布。参数β是分区先验分布(exp(-j))的相关参数。

贝叶斯序列分割技术对于高维稀疏数据的密度估计准确率也存在不足之处，本文使用copula变换提高对高维数据的处理效果。将每个维度的边际密度估计与copula变换的联合密度估计的乘积作为最终的密度估计结果。为copula变换空间的每个维度设立边界[0,1]。

1.3 概率密度估计方法

假设一个D维数据集共有N个数据实例，原贝叶斯序列分割算法将全部数据集作为样本空间Ω，然后将Ω分为若干的子区域，基于每个子区域的数据量和体积估计子区域的密度。

为了减少计算复杂度，使用贝叶斯序列分割技术估计每个子区域的密度。本文的贝叶斯序列分割算法在训练阶段首先将样本空间均匀分为B个子分区，每个分区b视为原样本空间的一个近似，记为Ω(b)(b=1,2,…,B)，每个分区包含L=N/B个数据实例。使用贝叶斯序列分割技术独立处理每个分区，最终获得B个子分区的集合及其相应的密度，该集合包含了B个概率密度的估计。

(5)

根据Sklar定理[11]，任意的多元分布均可以转换为带变量边际分布的形式，将一个有限维的联合分布分解为它的边缘分布和一个表示结构关系的copula函数，copula函数描述了变量间的相关性和一致性。

(1) 估计边际密度。首先估计数据的边际密度，使用边际密度获得累积分布函数(Cumulative Distribution Function,CDF)，使用边际CDF在copula空间内构建一个多维的密度分区，获得一个均匀边际分布的D维样本空间，记为[0,1]D。

基于边际密度和copula变换空间的密度，可获得测试数据z的总密度：

(6)

式中:fd为边际密度;Fd为对应的边际CDF;对copula相关性进行求导可计算出c。

(2) 维度对齐。上文对B个数据分区进行了不同维度的扩展，所以获得的样本空间大小不等。本文将CDF的范围限定为[0,1]，copula变换域不存在空间不等的问题，因此，计算B个分区的平均值仅需要对齐B个样本空间。因为所有的边际密度均为一维空间，所以设计了高效的维度对齐方法。对齐方法的步骤为：

Step1在B个分区中搜索最小数据扩展和最大数据扩展。

Step2为B个分区的所有扩展设立相同的边界。

Step3扩展每个分区密度的开始部分和结尾部分，与设立的边界对齐。

Step4重新计算修改后分区的边际密度，分区的数据点数量保持不变。

Step5使用更新的边际密度计算新的CDF。

图1 维度对齐方法的示意图

最终使用边际密度和copula变换密度计算每个分区的密度，将每个分区的密度代入式(5)产生最终的概率密度估计函数。

1.4 概率密度函数的度量方法

信息领域存在多个常用的多样性距离度量方法，如Kullback-Leibler divergence，但大多数方法为非对称方法，且计算效率低，多样性度量方法(Integrated Squared Error,ISE)是其中计算效率较高的一种方法，本文采用ISE计算两个概率密度函数之间的距离，ISE的计算方法为：

(7)

式中：p和q表示两个概率密度函数，p和q越接近，ISE(p,q)则越接近0。

2 时间序列在线分类算法设计

本文方法将时间序列观察表示为概率密度函数，利用K近邻(K Nearest Neighbor,KNN)模型将概率密度函数在线分类。首先，通过时间延迟嵌入将时间序列数据投影到重建相位空间，图2(b)所示是重建相位空间的实例图。然后，采用本文基于贝叶斯序列分割方法基于重建相位空间的观察估计其概率密度函数，如图2(c)所示。之后，使用积分平方误差计算概率密度函数间的相似性，建立所有概率密度函数的相似性矩阵。最终，使用KNN算法将时间序列分类。

图2 时间序列的处理实例图

因为重建相位空间能够表示非线性动态时间序列数据的时间模式，将混沌不规则的时间序列映射到重建相位空间能够增强时间序列的信息量，有利于后期的密度估计和距离度量处理。

2.1 建立相似性矩阵阶段

算法1为建立相似性矩阵的算法。输入参数包括：时间序列的观察训练集Tser[·],时间延迟嵌入方法的参数d和τ，以及密度估计的参数M，算法1采用核密度估计函数，M为核带宽参数，本文设M≥1。首先，运用时间延迟嵌入方法将时间序列观察s转化为重建相位空间sRPS，然后，基于贝叶斯序列分割的密度估计方法计算sRPS数据点的概率密度函数Tpdf[]。最终，输出所有时间序列的概率密度函数集Tpdf[]。

算法1建立相似性矩阵的算法

输入：Tser[],d,τ,h。

输出：Tpdf[]。

1.i=0；

2.forsinTser[] do

3.sRPS= delay_embed(s,d,τ);

//延迟嵌入

4.Tpdf[i] = density_est(sRPS,M);

//估计密度

5.i++;

6.end for

2.2 分类阶段

算法2为时间序列在线分类算法。输入参数包括：时间序列观察s,时间序列观测的概率密度函数集Tpdf,时间延迟嵌入的模型参数d和τ,密度估计的参数M,KNN的近邻数量k。

首先，将时间序列观察s转化为概率密度函数，运用时间延迟嵌入方法处理s。然后，采用密度估计算法计算sRPS的概率密度函数。使用积分平方误差计算目标时间序列概率密度函数和训练集概率密度函数之间的距离。最终，运用KNN预测目标时间序列观察s的分类。

算法2时间序列在线分类算法

输入：s,Tpdf[],d,τ,h,k。

输出：cl。

1.sRPS= delay_embed(s,d,τ);

//延迟嵌入

2.pdf= density_est(sRPS,h);

//估计密度,h=0.1

3.i=0;

4.forpinTpdf[] do

3.DISE[i]=ISE(pdf,p);

//计算积分平方误差

4.i++;

5.end for

6.cl= KNN(DISE[·],k)；

2.3 算法的计算复杂度分析

将长度为N的时间序列转化为d维重建相位空间的程序中，需要运行(N-(d-1)τ)×d次的时间延迟嵌入。因为训练集的M个时间序列均需要该处理，所以共需要M×(N-(d-1)τ)×d次的时间延迟嵌入。

在时间序列的分类程序中，需要计算全部训练时间序列的积分平方误差，该过程包含两个循环体。平方误差的计算次数等于时间序列重建相位空间矩阵的行数，即(N-(d-1)τ)。计算每个测试时间序列和训练时间序列间积分平方误差的复杂度为(N-(d-1)τ)2×d。

最终，时间序列分类的总复杂度为O(M×(N-(d-1)τ)2×d)，其中:M为训练集的时间序列数量;N为copula变换一维空间的维度。因此本文分类算法对于时间序列的维度具有鲁棒性。

3 仿真实验和结果分析

实验环境为Intel i7-3820 CPU，主频为3.6 GHz，内存为32 GB。基于MATLAB编程实现实验中的所有算法。

3.1 实验数据集

从UCR时间序列分类数据集[12]中选择7个维度高于200的数据集，评测本文方法对于高维时间序列的分类性能。首先使用z-score将7个数据集归一化处理，然后将数据集分为训练集和测试集。表1为实验数据集的基本属性，7个数据集来自于不同的领域。这7个数据集被许多时间序列分类文献所采用，因此便于完成对比实验和分析。

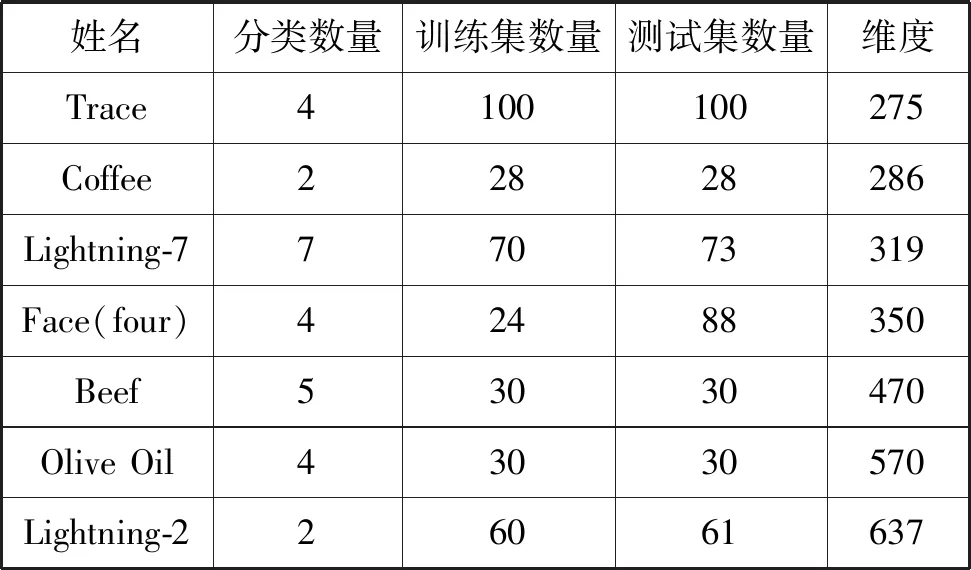
表1 实验数据集的基本属性

3.2 密度估计实验

首先从两个角度评估本文基于贝叶斯序列分割的密度估计算法性能，所考虑的性能指标为密度估计误差和计算时间。

(1) 密度估计的准确性。为了观察密度估计的细节信息，该组实验采用了人工合成的数据集，随机生成服从多元高斯分布的合成数据集，数据集共有400个数据，维度为16，前2个维度的数据服从三峰值的正态分布，第3个维度的数据服从单峰的正态分布，4～64维的数据服从双峰值的正态分布。对于不同分区大小分别测试密度估计的性能。采用KL散度(Kullback Leibler Divergence,KLD)评估密度估计算法的准确率，图3为密度估计的KLD结果，图中分别将每个分区的数据数量设为10、40和80。结果显示，分区的数据量越大，KLD的性能越好，当数据量大于100时，密度估计的准确性较好。

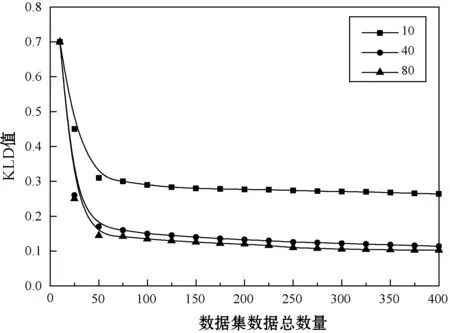
图3 密度估计的KLD结果

(2) 密度估计的时间性能。统计了估计B个块的密度所需的总时间，每个分区的大小为L=N/B。处理N个数据的总时间计算为：

(8)

式中:tov为计算平均密度的时间，可忽略不计;tL(N)为处理N个实例的总时间;L为分区的大小;B为分区的数量;tb(L)为处理第b个分区的时间。

图4为密度估计的时间结果，分区的数据量越大，处理时间越长。但本文算法对不同数据量的处理时间几乎为常量，因此本文方法同时适用于稳态数据流和非稳态数据流。

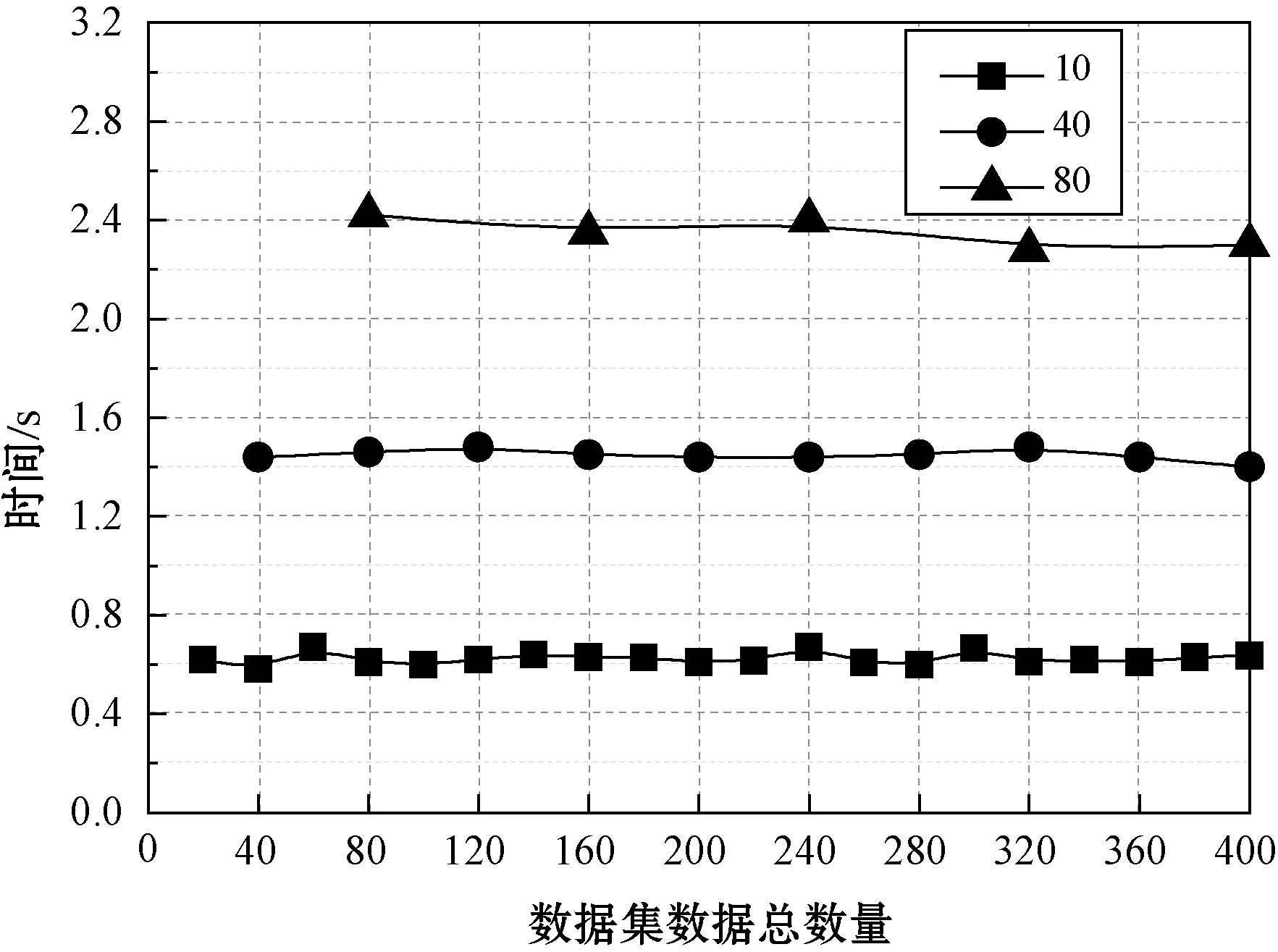
图4 密度估计的时间结果

3.3 时间序列分类实验

目前主流的时间序列在线分类算法主要包括基于距离(基于密度)的分类方法和基于深度学习的分类方法两种类型，本文算法分别和这两种类型的分类方法作比较，深入评估本文方法的有效性。

1) 基于距离的时间序列分类方法。本文方法是一种基于距离的时间序列在线分类算法，首先选择4个经典的方法作为对比方法。

(1) 高斯混合模型和重建相位空间结合的分类方法(GMMRPS)[13]。该方法首先将时间序列投影到重建相位空间，然后利用高斯混合模型建模数据，再采用最大期望算法对时间序列分类。

(2) K近邻和欧氏距离结合的分类方法(KNNED)[14]。该方法将时间序列表示为t维空间的一个向量，采用欧氏距离度量测试时间序列和训练时间序列之间的距离，从而对测试样本进行实时分类。该算法易于实现，且计算效率较高，但对于序列不对准较为敏感。

(3) K近邻和动态时间规整结合的分类方法(1NNDTW)[15]。该方法与KNNED较为相似，不同之处主要在于采用动态时间规整表示时间序列。

(4) 基于动态时间规整的快速分类算法(SDTW)[16]。该方法设计了时间序列的质量评价方法，并对低质量的部分时间序列提前剪枝，从而实现加速分类的目标。

图5为基于距离分类方法的分类准确率结果，可看出，GMMRPS和KNNED对于高维数据集的准确率均较低，GMMRPS的高斯混合模型对于高维数据的度量效果较差，KNNED的欧氏距离对高维数据的度量效果也较差。KNNDTW和SDTW两种基于动态时间规则的分类方法实现了较高的准确率，但随着维度的提高，这两种方法的分类准确率呈现明显的下降趋势。本文方法对于7个数据集均实现了较为理想的分类准确性，并且对数据维度显示出明显的鲁棒性。

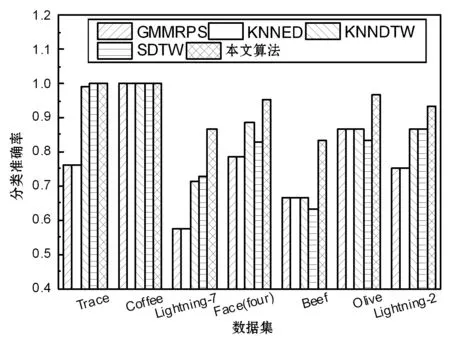
图5 基于距离时间序列分类方法的准确率结果

2) 基于深度学习的时间序列分类方法。深度学习技术是近期性能极好的一种学习方法，选择3个经典的深度学习方法作为对比方法。

(1) 基于多层感知机的分类方法(MLP)[17]。该方法的神经网络包含三个隐层，每层包含500个神经元，采用ReLU激活函数，采用softmax作为输出层。

(2) 基于全卷积神经网络的分类方法(FCN)[18]。该方法的神经网络包含3个隐层，滤波器数量为128 256 128，采用全局池化机制，采用softmax作为输出层。

(3) 基于残差神经网络的分类方法(resnet)[19]。该方法的神经网络包含3个残差块，每个残差块包含3个隐层神经元 ，采用全局池化机制，采用softmax作为输出层。

图6为基于深度学习分类方法的分类准确率结果，总体而言，基于深度学习的方法优于基于距离的方法。多层感知机对于高维时间序列的准确率较低，FCN和resnet两种基于深度学习的分类方法实现了较高的准确率，但随着维度升高，这两种方法的分类准确率呈现明显的下降趋势。本文方法对于7个数据集均实现了较为理想的分类准确性，并且对数据维度显示出明显的鲁棒性。

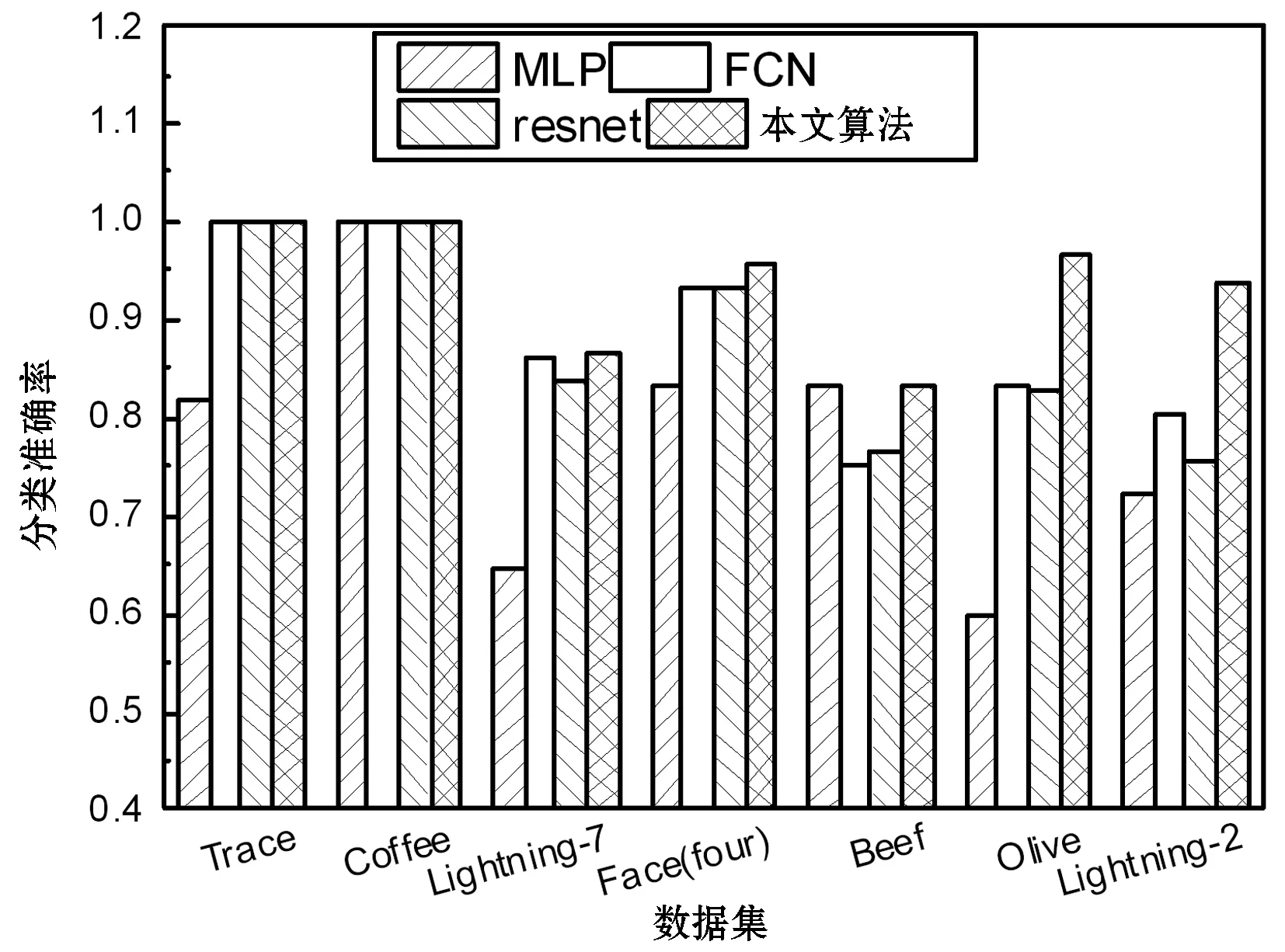
图6 基于深度学习时间序列分类方法的准确率结果

4 结 语

重建相位空间能够表示非线性动态时间序列数据的时间模式，将混沌不规则的时间序列映射到重建相位空间能够增强时间序列的信息量，有利于后期的密度估计和距离度量处理。贝叶斯序列分割技术对于数据的维度具有鲁棒性，本文将贝叶斯序列分割技术应用于时间序列的在线密度估计模型，对高维时间序列进行快速、准确的密度估计。在基于多组高维数据集上进行仿真实验，本文方法的时间性能和分类准确率均对时间序列的维度具有鲁棒性，并且实现了较好的分类准确率。目前本文仅考虑了常规的高维时间序列问题，未来将研究本文方法在演化高维数据流和混沌高维时间序列等问题上的应用，扩大本文方法的应用价值。