一种改进的并行蝙蝠算法
李广强 张肇宝 徐 晨 梁大伟 赵钎伊 于浩淼
(大连海事大学船舶电气工程学院 辽宁 大连 116026)
0 引 言
近年来随着人工智能领域迅速发展,群智能算法作为其中重要的组成部分得到了学术界的广泛关注,学者相继提出了粒子群算法[1]、人工蜂群算法[2]、随机蛙跳算法[3]、蝙蝠算法(BA)[4]等群智能算法,这些算法已用于解决路径规划[5]、网络检测[6]和数据分析[7]等问题[8-10],并取得了较好的效果。
BA是Yang[4]提出的一种较为新颖的元启发式算法。与其他群智能算法一样,其具有结构简单、鲁棒性强等特点,但仍然存在着易陷入局部最优、收敛速度慢和精度低等问题[11]。针对这些不足,国内外学者提出了不同的改进方法[12-15]。李煜等[16]提出了一种融合均匀变异和高斯变异的蝙蝠算法,引入变异开关函数,利用两种变异共同协作来提高算法的收敛精度。吕石磊等[17]引入自适应步长机制和变异策略,避免了算法陷入局部最优的问题,并提高了收敛精度。Cui等[18]则提出了基于黄金分割的主成分分析法的蝙蝠算法,降低了算法发生早熟收敛的可能性。耿艳香等[19]为了增强个体之间的信息交流,引入RNA遗传算法,以及通过信息的交叉和变异等措施,提高了算法的整体寻优能力。
基于上述工作,针对BA的不足,本文提出了一种改进的并行蝙蝠算法(IPBA)。首先利用混沌映射对初始值的敏感性和遍历性等特点,并结合免疫浓度的思想,给出一种基于免疫浓度的混沌初始化。然后引入并行策略,将初始种群均分为探索与开发两个子群体,子群体采用不同的惯性权重和停滞变异策略分别独立进化。给出的非线性指数递减的惯性权重系数可平衡算法在不同时期的全局搜索和局部开发能力,停滞变异策略也可有效防止算法陷入局部最优。同时子群体间定期进行个体迁移和信息交换,充分发挥并行优势,以提高算法整体寻优能力。最后采用若干经典函数优化测试,来验证IPBA的可行性和有效性。
1 基本蝙蝠算法

fi=fmin+(fmax-fmin)β
(1)
(2)
(3)
式中:fmin和fmax分别为频率f的最小值和最大值;β∈[0,1]为服从均匀分布的随机变量;x*表示当前全局最优位置解;i=1,2,…,N,N为种群规模。
对于局部搜索则是在位置和速度更新后,以一定概率在最优位置附近产生局部的新解:
xnew=xold+εAt
(4)
式中:ε是[-1,1]之间的随机数;At表示这一代所有蝙蝠的平均响度。

(5)
(6)

基本蝙蝠算法的算法步骤如下:
Step1在搜索空间里随机初始化种群,其中包括蝙蝠i的位置xi、速度vi、脉冲发射率ri、响度Ai,i=1,2,…,N,并找出当前的最优解位置x*。
Step2根据式(1)-式(3)更新每只蝙蝠的位置和速度。
Step3产生一个随机数rand,如果rand>ri,则利用式(4)在最优解x*附近产生一个局部解xnew。
Step4再产生一个随机数rand,如果rand Step5如果fnew Step6重复Step 2-Step 5的迭代过程,直到达到终止条件。 Step7输出全局最优解。 2.1.1混沌映射 混沌是自然界普遍存在的一种非线性现象,具有遍历性、随机性和对初始值敏感性的特点,即混沌序列能够在某一范围内不重复地遍历所有状态,使序列散布于搜索空间中,一定限度上提高了序列的质量。本文则采用具有较好遍历性的立方映射[20]。立方映射的表达式如下: y(n+1)=4y(n)3-3y(n) (7) 式中:-1≤y(n)≤1,n=1,2,…,N1。 对于D维空间中的N1个个体的生成步骤如下: Step1首先随机产生一个D维向量y1=(y11,y12,…,y1D),将y1作为第一个序列,其中-1≤y1k≤1,k=1,2,…,D。 Step2将y1的每一维都利用式(7)进行计算,通过N1-1次迭代后,产生其余的N1-1个个体。 Step3将N1个序列按式(8)映射到解的搜索空间。 (8) 式中:xik表示第i个个体在搜索空间中第k维上的坐标;kmin、kmax表示搜索空间中第k维上的下限和上限。 在免疫算法[21]中,抗体(本文指蝙蝠个体)的浓度是指与某一抗体相同或相近的抗体在抗体群中所占的比例。在免疫算法中,一些适应度高且浓度低的抗体得到促进,生存概率较大,而适应度低、浓度高的抗体则会得到抑制,生存概率较小。因此将混沌映射结合免疫浓度的思想,提出一种基于免疫浓度的混沌初始化,得到一些高质量的初始个体。 计算抗体浓度的公式为: (9) 式中:N1为混沌种群规模;Auv为抗体u和抗体v的亲和度。亲和度是指两个抗体的相似程度。常见的亲和度计算方法有基于欧氏距离的计算方法、基于矢量距的计算方法等。在本文中欧氏距离的计算方法更能表示两个抗体之间的距离相似度,因此采用此方法来表示两个抗体之间的亲和度,亲和度公式为: (10) 为了得到质量较好的初始群体,根据抗体的适应度和浓度的共同作用对其进行选择。以极小化问题为例,抗体u的综合目标值pu计算公式为: (11) 式中:f(u)表示抗体u的目标函数值,在极小化问题中适应度越大,说明抗体的目标函数值越小;θ为比例因子,决定了适应度与浓度的作用大小,本文选择θ=0.5。根据立方映射产生的N1个抗体,利用式(11)计算得出每个抗体的综合目标值p,并从小到大排序,从中选择出表征适应度大、浓度低的前N个抗体作为初始种群。由此可得到较好的初始群体,为后续的算法操作奠定了良好基础。 从速度更新公式可以看出,通过改变速度项系数,能调节算法的探索能力和开发能力。针对此问题,许多学者对蝙蝠算法作出了相应的改进。王皓等[22]基于开发能力和探索能力相均衡的思想提出了全局邻域搜索策略,整体的动态惯性权重值呈现减小趋势,这有利于平衡算法的全局搜索和局部搜索,同时增加了种群的多样性。裴宇航等[23]则采用一种服从均匀分布和贝塔分布的随机调整策略,动态地调整惯性权重的大小,以提高种群的收敛速度。 10月11日,上海译文社发表声明指出,“我社于2017年11月获得原著权利人唯一授权,在中国大陆境内独家出版原著中文简体字版,并约定书名为《低欲望社会》”,但有出版社“借‘低欲望社会’之名,出版了大前研一先生的另一部作品”,引发混淆与误导,涉嫌不正当竞争…… 本文采用一种非线性递减的惯性权重ωt。在前期,ωt较大使算法具有较强的全局搜索能力,加快了算法的收敛速度。随着迭代的进行,ωt以指数的形式逐渐减小,使算法的局部搜索能力增强。这种递减的惯性权重可以有效地平衡算法在不同时期的全局搜索和局部开发能力,提高了算法的收敛速度和精度。本文的惯性权重ωt表达公式定义为: (12) 因而,速度更新公式变为: (13) 式中:t为算法的当前迭代次数;T为算法的最大迭代次数;μ、ωa和ωb均为常数。 为进一步改善算法早熟收敛、易陷入局部最优的缺陷,引入一种停滞变异策略。本文算法在寻优过程中对最优解进行监测,设置一个停滞阈值δ。如果连续δ代记忆的最优解未更新,则再次进入局部搜索时,引入个体维度变异,维度变异的数量在每次迭代中取值不同,主要取决于个体的适应度。一般地,适应度越小,变异的维度越多;适应度越大,变异的维度越少。算法在不同时期变异维度的数量不同,该策略可自适应而有效地避免算法陷入局部最优。在前期,群体中的个体适应度普遍较小,因而变异维度的数量,大概率越多,这有利于算法抗早熟,跳出局部最优;而后期的情况正好相反,这在避免算法陷入局部最优的同时,更加强了算法局部搜索的能力。 变异个体的维度数量Num的表达公式为: (14) 式中:int(·)为取整函数。 个体i的第k(k=1,2,…,Num)维变异公式为: (15) 为了有效地避免算法早熟,增加种群的多样性,以及平衡算法的探索能力和开发能力,本文采用一种并行策略。其基本思想是:首先将基于免疫浓度思想生成的混沌初始种群分为探索子群体1和开发子群体2,两个子群体采用不同参数的惯性权重和停滞变异策略分别独立进化,可均衡算法探索和开发之间的能力。设置参数T1,每隔T1代,群体间就进行个体迁移和信息交换,由此通过两群体间的交换信息方式,可充分发挥并行优势,提高算法整体性能。子群体之间的个体替换采用对等替换的策略,每一子群体独立进化若干代后,按目标函数值排序,选择出其中较为优秀的NB个个体,替换掉另一个群体中相应数量较差的个体。 本文算法的两子群体惯性权重和停滞变异策略的相关参数设置不同,使其分别注重探索和开发,进一步避免由于采用单一种群而易于陷入局部最优的问题。根据多次的仿真计算比较,本文算法相关参数设置如表1所示,其中:ωa、ωb表示惯性权重设定的相关常数;δ表示停滞变异中的停滞代数阈值。 表1 子群体惯性权重以及停滞变异的参数设置 IPBA具体流程如图1所示。 图1 IPBA流程 以极小化问题为例,IPBA步骤如下: Step1基于免疫浓度的混沌初始化思想,产生初始种群xi(i=1,2,…,N),以及随机产生蝙蝠i的速度vi、响度Ai和脉冲发射率ri,并将初始种群均分为两个子群体。 Step2两子群体分别按照式(1)、式(3)、式(13)产生新的速度和位置。 Step3对于每个子群体产生一个随机数rand,分别在两个子群体进行比较,如果rand>ri,则利用式(4),在最优解x*附近产生一个局部解。并对最优解进行监测,如果连续多代没有得到更新,说明可能陷入局部最优,那么再次进入局部搜索时,进行变异操作,采用式(14)、式(15)产生新的局部解,有助于防早熟。 Step4分别在两个子群体中产生一个随机数rand,如果rand Step5分别在两个子群体中判定fnew Step6在每隔T1代进行两个子群体的信息交换。 Step7重复Step 2-Step 6的迭代过程,直到达到算法的最大迭代次数。 Step8输出全局最优解。 为了验证IPBA的有效性和可行性,选用若干个经典函数,如表2所示,进行相关仿真验证,经典函数的最优值皆为0。 表2 测试函数 续表2 本文选取的对比算法包括基本的蝙蝠算法(BA)、文献[23]中采用动态惯性权重的自适应蝙蝠算法(DAWBA)、文献[24]提出的具有记忆特征的改进蝙蝠算法(MCBA)。各算法的参数设置如下:在IPBA中,最大频率fmax=2,最小频率fmin=0,最大响度Amax=0.5,最小响度Amin=0,脉冲发生率r0=0.5;在DAWBA中,最大响度Amax=0.25,最小响度Amin=0,最大频率、最小频率和脉冲发射率与IPBA相同;在MCBA中,最大频率fmax=100,最小频率fmin=0,其他参数设置与IPBA相同。为了保证实验仿真的公平性,所有算法的种群规模选择为40,最大迭代次数为1 000次。 所有的仿真环境都为CPU i3-8100,内存8 GB的计算机,在MATLAB软件平台上进行。 为了验证惯性权重对算法性能的影响,在参数设置相同的情况下,对加入惯性权重、未加入惯性权重及惯性权重中μ不同取值进行仿真。μ=0表示未加入惯性权重。表3给出了各算法在20维空间中运行20次的仿真结果,其中包括算法的最优解best、最差解worst和平均值mean。 续表3 可以看出,当加入惯性权重后,虽然惯性权重中μ的取值不同,但加入惯性权重的算法平均值、最优解、最差解都有一定程度的提高,说明惯性权重在算法中起到了较大的作用。当μ的值逐渐增大到一定值后,算法的平均值及最优值呈现下降的趋势,在f5中最为明显,而在其他函数中相对也有较小的下降趋势。综合μ的不同取值所得到的数据结果,当μ=10时,算法的整体效果最好。 为了验证IPBA的可行性和有效性,选用f1-f6经典函数进行相关仿真验证。将这些算法分别在10、30维空间中独立运行20次,统计出所有算法所得最优解best、最差解worst和优化结果平均值mean,数据结果如表4和表5所示。 表4 算法求解10维测试函数结果 表5 算法求解30维测试函数结果 4.3.1收敛精度分析 由表4和表5可以看出,在相同维度下,IPBA所得到的最差解、最优解及平均值均优于BA。而与DAWBA、MCBA相比,在表4、表5中的f5函数及表5的f4函数,IPBA所得的平均值比MCBA差,但在其他函数中IPBA的平均值均优于DAWBA、MCBA。在不同维度下,各算法的收敛精度随着维度的增加而降低,但IPBA仍然能得到不错的最优解。例如在表4和表5中的f2函数,其在搜索空间中存在着大量的局部极值,随着维度的增加,MCBA和DAWBA均陷入到了局部最优中,而IPBA由于引入并行和停滞变异等策略,均衡了算法在探索与开发之间的能力,有效避免了算法陷入局部最优,提高了算法的寻优能力。同时观察f1-f6函数在10、30维空间中的数据结果,IPBA所得到的大部分最优解与最差解的收敛精度相差不大,与相关算法相比,其精度更高,收敛精度也有一定提高,说明了IPBA具有更好的整体寻优能力及良好的稳定性。 为了更充分地进行对比,选用f2-f4、f7-f10函数将本文的IPBA与文献[25-26]的MBA和ACEBA的优化数据进行对比,如表6所示。可以看出,虽然在f3函数中,IPBA在平均值上劣于MBA,但在f2、f7函数中,IPBA在平均值精度上都明显优于MBA。而对于ACEBA,其采用自适应的进化框架使参数能够自适应调整,令算法更具智能性。但对于复杂的测试函数,如f8-f10,ACEBA的收敛精度明显劣于IPBA,其中最明显的是f8函数。IPBA所得平均值优于ACEBA 13个数量级,且其最优解也相对提高了13个数量级。综合表4-表6的数据结果,对大部分函数的仿真测试,IPBA都取得了较好的收敛效果。 表6 IPBA与已发表文献中的数据对比结果 4.3.2收敛速度分析 算法的收敛曲线可以直观地反映算法陷入局部最优以及收敛速度的情况,是衡量算法性能的重要评价指标。本文给出算法分别在10、30维空间中的收敛曲线,如图2和图3所示。首先从同维度不同函数进行分析,f2函数是一种利用增加一个余弦调制函数项来频繁的产生局部最小值的多峰函数,它可以用来检测算法的可行性。由图2(b)可见,BA、DAWBA、MCBA在面对此类多峰函数优化问题时,无法跳出局部最优,而IPBA具有良好的寻优能力。其主要原因是IPBA采用并行、停滞变异等策略,并在寻优过程中对算法进行监控,有效地避免了算法陷入局部最优。而且在多峰函数f4(如图2(d)所示)中,IPBA的收敛效果也优于BA和DAWBA,但劣于MCBA。图2(b)和图2(d)有算法早熟,故无法更好地比较各个算法在优化多峰问题中的算法收敛速度,故观察图2(c)。图2(c)是f3函数在10维空间的收敛曲线,f3函数也存在着大量局部极值,可见BA、DAWBA、MCBA和IPBA都可跳出局部最优,但IPBA的收敛速度明显优于其他算法。在图2(e)、图2(f)中,IPBA的收敛速度优于BA,而与MCBA相近。进而,从相同函数的不同维度优化问题进行分析,这里仅改变算法的维度,在其他参数相同的环境下进行仿真。图2(b)和图3(b)中采用相同的多峰测试函数f2,对比可见算法的搜索难度增大,在大约100代时,DAWBA、MCBA、BA都陷入了局部极值中,而IPBA随着维度的增大,收敛的速度相对变缓,但在该多峰函数不同维度的优化中,都能较好地跳出局部,最后在500代左右收敛。而除图3(d)外的其他测试函数中,随着维度增加,搜索难度增大,IPBA的收敛速度仍然优于其他算法。综上,在大部分的测试函数中,IPBA都能通过惯性权重和停滞变异策略,以及发挥算法的并行优势来解决易陷入局部最优的问题,从而增加算法的整体寻优效果。 (c) f3收敛曲线 (e) f5收敛曲线 (a) f1收敛曲线 (a) f1收敛曲线 通常执行算法所需要的计算工作量用时间复杂度表示。算法的时间复杂度越大,所要执行基本语句的次数越多,则它所花费的时间也就越多,能更直观地反映出算法性能。因此需要对BA和IPBA进行相关的时间复杂度分析。 按照基本BA的算法流程,初始化种群的时间复杂度为O(ND),其中N表示种群规模,D为优化问题的维度。设置种群的迭代次数为T,在T次迭代中,蝙蝠的速度和位置变化的时间复杂度为O(NDT)。BA的总体时间复杂度为O(NDT+ND)。 本文提出了一种改进的并行蝙蝠算法(IPBA)。首先采用一种基于免疫浓度的混沌初始化,生成质量较好的初始种群。然后引入并行策略,将种群分为探索与开发两个子群体,采用不同的非线性递减惯性权重和停滞变异策略分别进化。其中惯性权重可有效地平衡算法不同时期的全局搜索和局部开发能力,而提出的停滞变异策略也可防止算法陷入局部最优,并增加局部搜索能力。同时子群体间定期进行个体迁移和信息交换,发挥并行优势,提高算法的整体性能。最后通过经典函数进行仿真测试,并进行相关分析,充分验证了所提算法的可行性和有效性。2 改进算法设计
2.1 基于免疫浓度的混沌初始化
2.2 惯性权重
2.3 停滞变异策略

2.4 并行策略
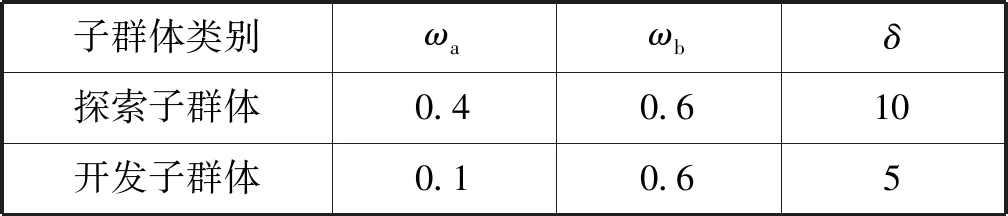
3 改进算法流程

4 仿真实验及结果分析
4.1 测试函数及参数设置
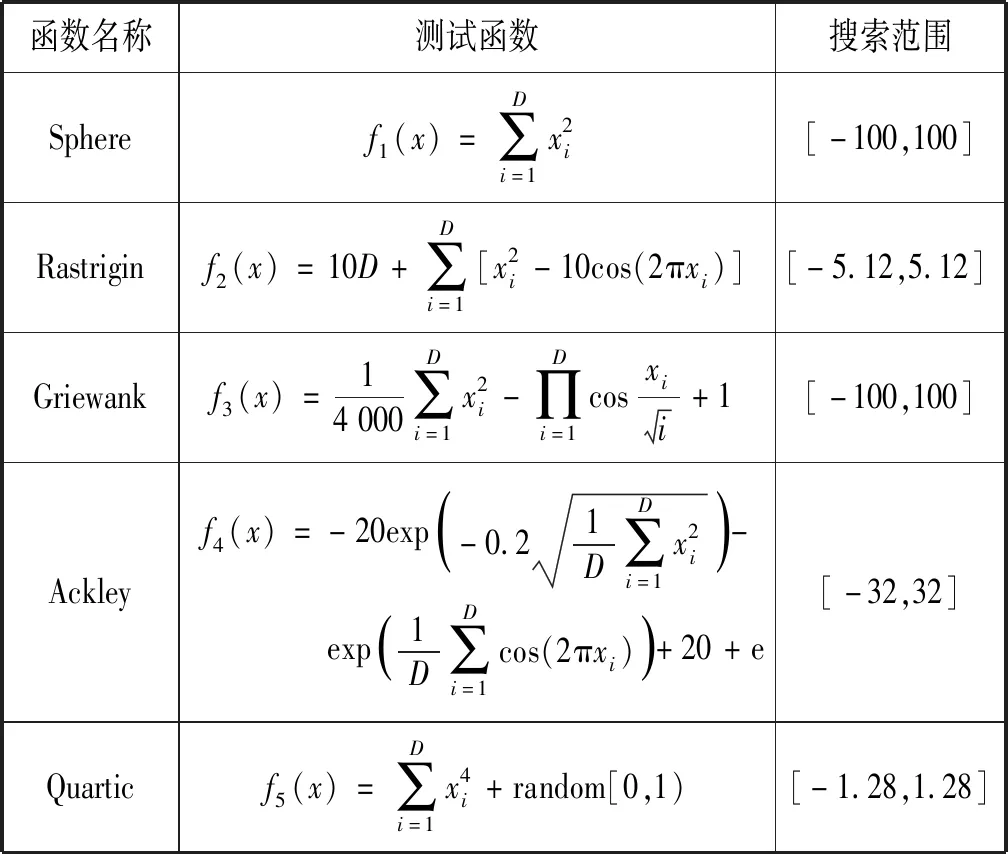
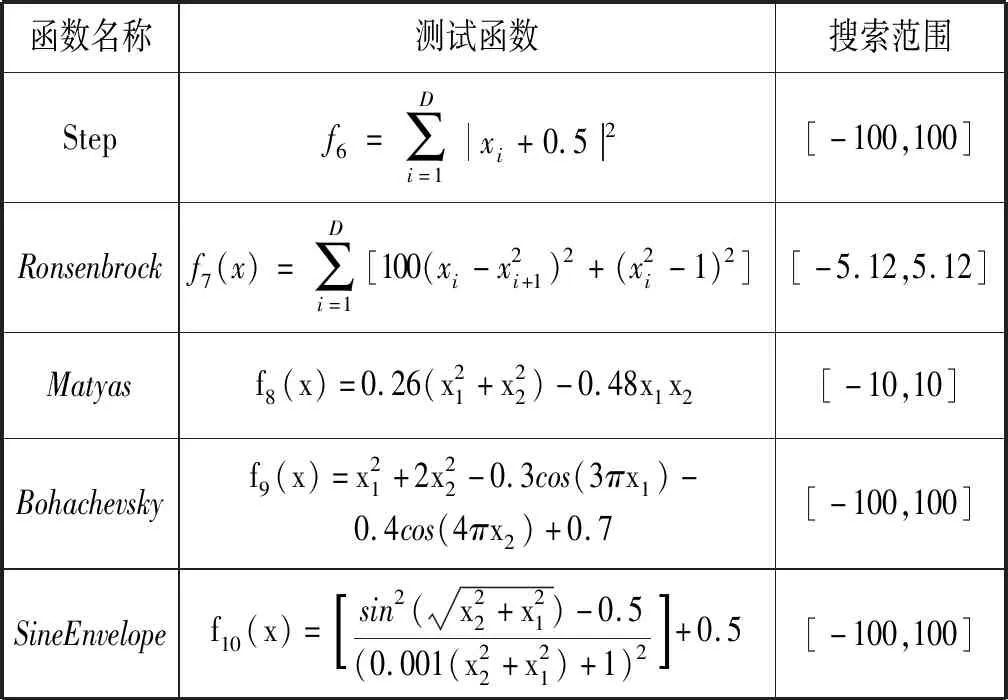
4.2 惯性权重的性能分析及μ值确定
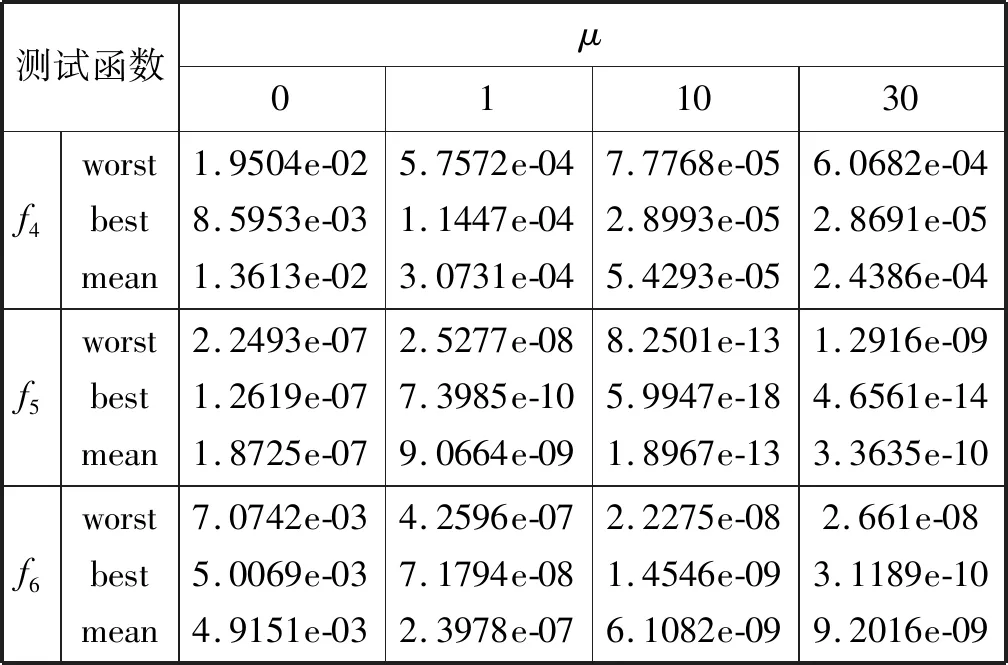
4.3 收敛精度及收敛速度分析






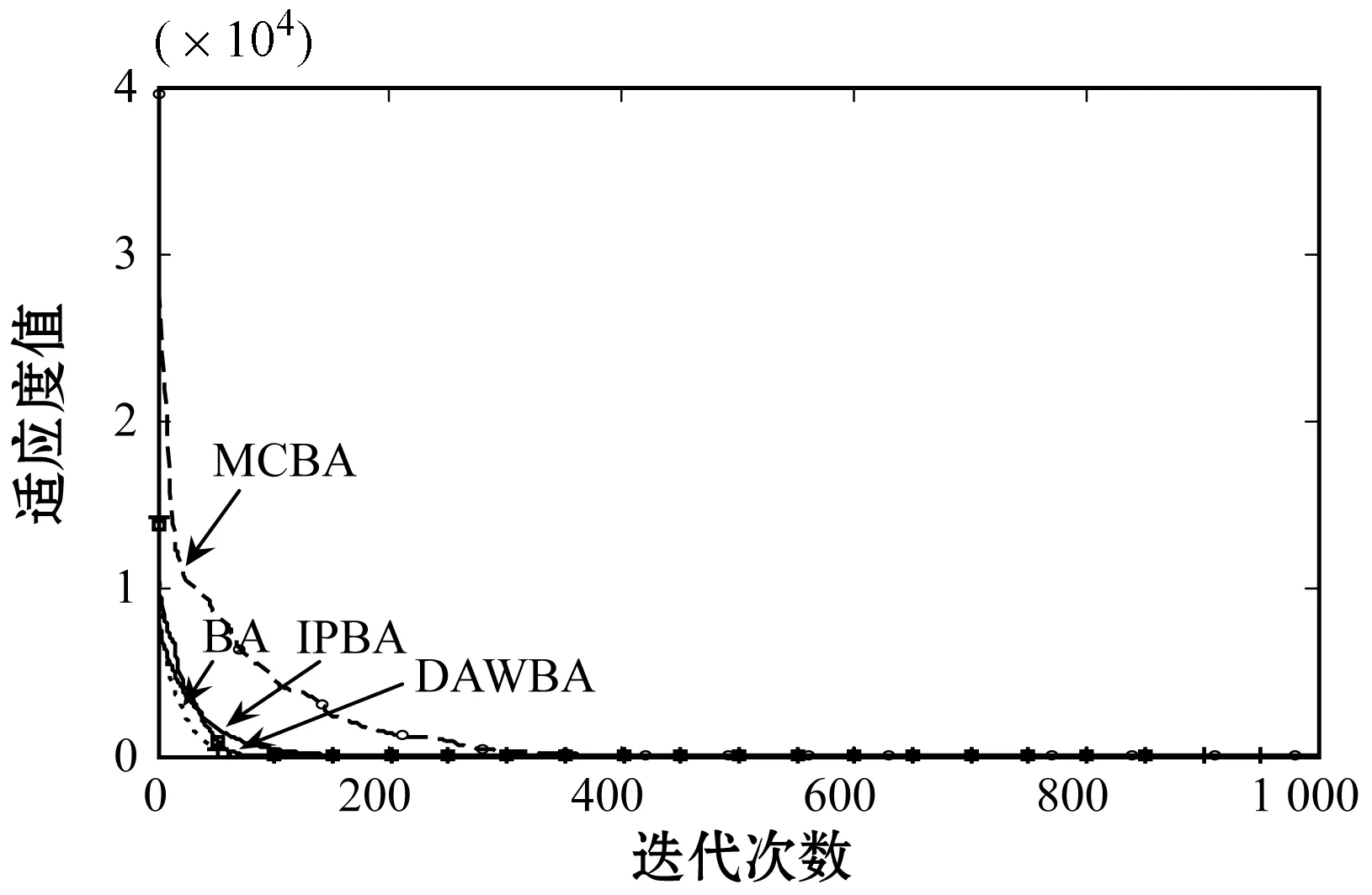
4.4 时间复杂度分析
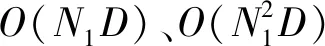
5 结 语

