改进的Retinex低照度图像清晰化处理

赵征鹏 李俊钢 普园媛,2

1(云南大学信息学院 云南 昆明 650504)2(云南省高校物联网技术及应用重点实验室 云南 昆明 650504)

0 引 言

在军事和民用的各个领域，图像处理技术随处可见，尤其是在模式识别、目标识别、故障诊断、远程探测、卫星遥感等领域展示了较高的应用性。图像处理可以划分为多种技术：图像增强、图像降噪和图像修复等。其中的图像增强技术，可以将原来模糊且辨识度低的图像变得清晰，提升识别和判读图像的效果，满足某些特定场合的需求[1-3]。

在实际生活中，有很多图片的效果都不尽如人意，尤其是低照度图片[4]。由于在拍摄时，入射光线的不足，导致图片整体较暗，看不清其中的细节。鉴于这种情况，本文可以借助相应的图像增强方法[5-7]来提取亮度图像。Retinex算法就是常用的一种图像增强处理算法。然而在传统的Retinex算法中，处理过后的图片容易产生图像“光晕”、色彩流失等问题，这是因为同一空间的滤波模块应用在了所有像素之上[8]。为了降低该现象对图像质量造成的影响，本文提出了改进的单尺度Retinex算法。

1 基本原理

1.1 Retinex理论基础模型

1963年由Edwin.H.Land提出的Retinex理论，是一种建立在科学实验与分析基础上的图像增强方法[9]。Retinex理论也常被称作是“视网膜皮层理论”，这是因为Retinex是视网膜(retina)和皮层(cortex)的合成词[10]。最初基于Retinex理论模型所提出的个人视觉系统 (Human Visual System，HVS)，解释了人眼对于光线波长和亮度互不对应的原因。在该理论中，两个因素决定了物体被观察到的颜色，即物体本身的反射性质和物体周围的光照强度，但根据颜色恒常性理论可知，物体自身的固有属性并不会受到光照的影响，而物体对于不同光波的反射能力在很大程度上决定了物体的颜色[11]。Retinex理论中，原始图像像素点的动态范围大小和光照强度有关，其本身的反射系数决定了原始固有属性。所以Retinex的思路是假设原始图像是由反射图像和光照图像相乘而得，为了保留住物体的固有属性，需要去除光照的影响。

如图1所示，假设人们所看到的图像为P(x，y)，则：

图1 Retinex 理论模型图

P(x,y)=Z(x,y)×F(x,y)

(1)

式中：Z(x,y)表示入射分量，即周围光照的强度信息；F(x,y)表示反射分量，即物体自身的固有性质。在基础的Retinex理论中，通常对式(1)两边同时取对数，这是因为: (1)人眼对亮度的感知能力不是线性的，它近似于对数曲线，如图2所示。(2)实数域的乘除运算通过取对数的操作将其转换到对数域，可以把复杂的乘除运算转换成简单的加减运算，这样可以简化算法的复杂性。

图2 人眼感知图

1.2 单尺度Retinex(SSR)

Retinex理论提出后不久，Jobson等[12]在其基础上提出了单尺度Retinex算法(Single-scale Retinex,SSR)。SSR算法的处理流程近似于人眼的视觉成像过程[13]。SSR算法的思想是：利用构建的高斯环绕函数分别对图像的R、G和B三通道进行低通滤波。经过低通滤波后所留下的就是光照分量，接着用对数域的原始图像减去对数域的光照分量，所得结果就是反射分量，即输出的结果图像。单尺度Retinex算法能压缩图像动态范围，可保持图像色彩并增强图像的细节[14]。单尺度Retinex算法的一般数学形式如下：

对式(1)两边同时取对数得：

log(P(x,y))=log(Z(x,y))+

log(F(x,y))

(2)

令：

(3)

则可得原图像的对数域表达式：

p(x,y)=z(x,y)+f(x,y)

(4)

所以反射图像对数域表达式为：

log(P(x,y))-log(P(x,y)*H(u,v))

(5)

式中：P(x,y)表示实数域原始图像；F(x,y)表示实数域反射图像(即待增强图像)；H(u,v)表示中心环绕函数；*是卷积运算符；log(P(x,y)*H(u,v))表示将原图和滤波函数做卷积处理，进行亮度图像的估计。

在传统SSR算法中，H(u，v)采用高斯环绕函数[15]G(x,y)，用高斯环绕函数与原图像进行卷积处理来进行亮度图像的提取。G(x,y)的构造如下：

(6)

式中：高斯环绕的尺度参数σ为算法中的唯一可调节参数。σ的取值容易影响增强效果：σ较小时，图像的细节信息能得到较好的保持，像素动态范围变大，但颜色会有所失真；σ较大时，会导致细节缺失，像素动态范围变小，但色彩保真度高。SSR 算法的基本流程如下：

(1) 输入原始图像P(x,y),把图像像素转换为浮点型。

(2) 调试并选择最佳的尺度参数σ，且其能满足∬G(x,y)dxdy=1。

(3) 式(1)两边取对数，用对数域的原始图像减去对数域的入射图像求得对数域的反射图像，记作f(x,y)。

(4) 求f(x,y)的实数域图像F(x,y)。

(5) 将实数域的图像F(x,y)进行线性拉伸并输出。

2 改进的单尺度Retinex算法

在图像处理过程中，传统的单尺度Retinex算法都要分别对彩色图片RGB空间的三个通道进行处理[16]。这样一来，不仅耗时，且RGB三个通道有着较高的关联性，若处理不当，难免会产生三个通道增强处理程度不均衡的现象，而且还会伴随着“光晕”现象、颜色失真、细节过增强等问题的出现。为了降低这些问题对图片质量的影响，本文的改进算法将彩色图片从RGB空间转换到HSV空间，对饱和度分量S做自适应线性拉伸，对亮度分量V做改进的Retinex算法增强，最后将图片再转换到RGB空间。

2.1 颜色空间的转换及线性拉伸

RGB颜色空间是最常用的颜色空间。在RGB空间中，每个分量所能表示的范围为[0，255][17]，R、G和B三个变量相结合可以表达较为完整的色彩信息。HSV颜色空间也是常用的颜色空间。在HSV各通道中，饱和度S指的是颜色的鲜艳程度，亮度V指的是颜色的明暗程度，色度H可以区分某一种颜色。在 HSV 空间模型[18]中，色度H与亮度V两两正交，将图片从RGB各通道转换到HSV各通道，再对亮度分量 V进行处理可以保证图片色彩信息不被改变。

然而，HSV 空间模型中，亮度V和饱和度S之间是相关联的，饱和度S升高，亮度V就会有所降低。所以为了保证图像的鲜艳程度，亮度V一旦改变，饱和度S也要做相应的改变。与此同时，图像在采集过程中，每幅图像的照度由于不同的外界环境而有所差异，这就需要对饱和度分量 S进行不同程度的自适应拉伸。因此，本文算法对饱和度分量S采用了一种自适应的拉伸方法，其表达式如下：

(7)

式中：S表示原始图像的饱和度分量；S′表示线性拉伸后图像的饱和度；max(R，G，B)和min(R，G，B)表示的是整幅图像灰度化的一个过程，分别表示彩色图像中三分量亮度的最大值和最小值；由于图像中有着不同颜色的物体，导致它们的灰度值也不同，Mv表示整幅原始图像的平均灰度值。从式(7)可知，饱和度比较低时，调整后并没有产生很大的变化；原饱和度越高，亮度变化越快，调整后的饱和度就会被增强，图片整体效果就会得到增强。

2.2 高斯低通滤波函数的替换

在传统的单尺度SSR算法中，利用高斯低通滤波器(Gaussian low-pass filter, GLPF)来进行亮度图像的提取。二维高斯低通滤波器的频率响应函数的表达式如下：

(8)

式中：D(u，v)是(u，v)点距频率矩形原点的距离，D0表示截止频率。

该方法虽可达到一定的图像增强效果，但有时会有“光晕”以及过增强现象的产生，这是因为GLPF“光滑陡直”的截止频率曲线其幅度随着截止频率的减小衰减更快，如图3所示。由于在某个区间上的频率变化较快，将其作用在图像的频谱上后，图像上的某些频率会被截断，导致图像频率变化不连续，这会导致像素缺失、图像细节丢失严重并伴有噪声。

图3 GLPF幅频特性曲线图

为了降低像素缺失以及细节丢失对图片质量的影响，本文根据巴特沃斯低通滤波器(Butterworth low-pass filter, BLPF)的特性[19]，将GLPF替换为一阶的BLPF。巴特沃斯低通滤波器的表达式如下：

(9)

BLPF的幅频特性曲线如图4所示，可以看出，当BLPF的阶数n=1时，其幅频特性曲线是“光滑平缓”的。将其作用于频谱后，能较好地保护图像频谱不被截断。

图4 BLPF幅频特性曲线图

为了进一步说明n=1的BLPF是“光滑平缓”的，图5是通过BLPF中心的4幅灰度级剖面图。它们的阶数分别为1、2、5、20，且截止频率都为5。

图5 通过BLPF中心的灰度级剖面图

可以看出，除了n=1的BLPF之外，其余的BLPF都有振铃现象的产生，尤其是n=20 时，BLPF的振铃现象很明显，这是因为当n=20时，其特性曲线几乎与频率轴垂直，此时可以将其视作一个理想低通滤波器，所以就产生了振铃现象。

通过上面的分析与讨论，用一阶的BLPF来进行亮度图像的提取，可以保护图像像素以及图像细节。本文将其记作SSR_BF(基于巴特沃思低通滤波的改进SSR算法)。改进算法如下：

根据SSR算法的数学表达式，用一阶的巴特沃斯低通滤波函数替换传统算法中的高斯环绕函数，此时的H(u,v)表示BLPF的滤波函数，即将式(9)代入式(5)，可得：

f(x,y)=logP(x,y)-

(10)

图6 SSR_BF算法流程

2.3 HSV空间的SSR_BF

在HSV空间中，H、S、V三个分量之间的关联性不大。提取亮度分量V并做相应的处理，不仅可以保持原始图像的色调H 与饱和度S的关系，还可以提升图像亮度，丰富图像细节以及保持图像的原始色彩信息。图片经过SSR_BF处理后，图像的像素以及细节得到了保护，但是因为其在RGB空间进行的处理，所以色彩会有所失真。为了解决颜色问题，本文将图片转到HSV空间各通道并对V分量进行SSR_BF的增强。

因为之前已经对S分量做了线性拉伸的操作，为了保证V分量与S分量之间的比例，对V分量进行SSR_BF算法的增强来提取亮度分量。这样一来，不仅可以压缩图像的动态范围，还可以提升其亮度并抑制高亮区的“光晕”现象。本文最终改进的清晰化算法流程如图7所示。

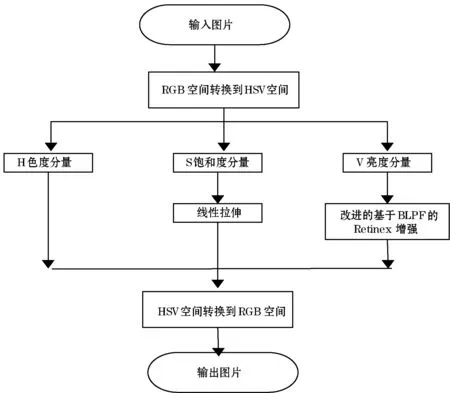
图7 清晰化算法流程

本文最终的改进清晰化算法步骤如下：

(1) 将图片从RGB各通道转换到HSV各通道。

(2) 在HSV的通道中，对饱和度分量S做自适应的线性拉伸，对亮度分量V做基于巴特沃斯低通滤波(BLPF)的改进SSR算法增强，H色度分量保持不变。

(3) 将处理好的图片从HSV空间各通道转换到RGB空间各通道。

(4) 输出图像。

3 实验与分析

为了进行本文算法有效性的实验，本实验环境为CPU 2.5 GHz，内存4 GB，Windows 7系统，利用MATLAB 2018a软件进行仿真实验。实验分两部分：(1) 本文算法处理低照度图像的可行性；(2) 本文算法与其他图像增强算法对低照度图像处理效果的对比。实验所使用的图片挑选自ground truth database 库里的图像数据(arborgreens包以及barcelona包)。实验中用到的对比算法有SSR算法、MSR算法、文献[20]的算法[20]、文献[21]的算法[21]，所使用的测试图片来源于网络。图像质量评价方法如图8所示。主观评价采用视觉观察；客观评价使用指标均方差和信息熵进行评价。亮度分布情况用均方差表示，均方差越小，亮度分布越均匀；图像细节、图像层次和图像信息用信息熵表示，越大越好。

图8 图像质量评价

3.1 本文算法的可行性

1) 滤波函数的替换和线性拉伸。传统的单尺度Retinex算法在处理过程中会有颜色失真等问题的出现，本节先进行SSR算法和SSR_BF算法的效果比较，结果如图9所示，图9(b)使用的是高斯低通滤波函数，图9(c)使用的是一阶的巴特沃斯低通滤波函数，然后在替换高斯低通滤波函数为巴特沃斯低通滤波函数的基础上，对比无线性拉伸(图9(c))和有线性拉伸(图9(d))的效果。实验中高斯低通滤波函数的尺度参数σ=250，巴特沃斯低通滤波函数的截止频率D0=5。

图9 算法可行性效果图

(1) 细节部分：从两组图中可以看出，用高斯低通滤波函数处理的图9(b)，两组都出现了颜色失真的现象，第一组中主体植物的叶子出现了过增强现象，第二组中树干产生了“光晕”，出现了伪彩色；但用巴特沃斯低通滤波函数处理的图9(c)中，凸显原图像细节的同时(第一组左上方框中的树干更清晰了)，在一定程度上抑制了图9(b)所产生的“光晕”以及过增强现象(抑制了第二组框中树干的“光晕”现象)。

(2) 颜色部分：对饱和度分量S没做线性拉伸的两组图9(c)，增强过后的图片色彩整体“泛白”，图片中树木花草等物体应有的颜色没有显现出来；但对饱和度分量S经过线性拉伸后，图片整体颜色鲜艳。第一组图9(d)中的主体植物的叶子更绿了(白框部分)，地上红色的落叶以及后方棕色的树干都展现了出来。第二组图9(d)中可以看到斑驳的金色阳光洒在绿色的树叶上(白框部分)。

2) 截止频率D0的确定。为了达到较好的增强效果，根据巴特沃斯低通滤波器的幅频特性曲线特点，本节对本文改进算法进行了不同截止频率D0的增强效果对比，实验结果见图10。

图10 不同截止频率效果图

可以看出，图片整体提亮，不同截止频率的增强效果图都凸显了原图所没有展示出来的细节：墙壁的纹路、亮着红灯的音响以及绿色的盆栽植物等，而且在追光灯的作用下，整幅图呈现出了淡红色的背景状态。在这其中，巴特沃斯低通滤波器中的截止频率D0主要起着对图像平滑的作用，图像平滑是指用于突出图像低频成分，抑制图像噪声的一种方法。D0越大，平滑效果越显著。通常来说，平滑会使图像亮度平缓渐变，减小突变梯度，保留主体像素，但会使图像变得模糊。不难看出，当D0=5时，平滑效果较好，随着D0的增加，图像逐渐模糊。为了保证改进算法的有效性和可行性，D0=5为本文改进算法的最佳截止频率。

所以综上所述，本文的改进算法对低照度图像具有一定的增强效果和可行性，主要表现在色彩保真和细节增强方面。

3.2 与其他处理算法的对比

1) 主观评价。为了进一步说明本文算法的有效性，本节将用本文算法与SSR算法、MSR算法、文献[20]算法、文献[21]算法进行对比。对比效果如图11-图12所示。

图11 小男孩效果图

图12 教堂效果图

通过各种算法的处理，图片整体提亮，但SSR算法出现了过增强现象；MSR算法使得小男孩整体轮廓不够清晰，整幅图色彩不够鲜艳；文献[20]算法的色彩和细节表现得不够；文献[21]算法虽然呈现了图像大部分细节，但清晰度不够。本文算法处理后，小男孩的整体轮廓清晰。本文算法在保持整幅图片色彩鲜艳的同时，也使小男孩鞋底的花纹以及图片右边墙壁的花纹清晰可见。

经SSR算法处理过后，整体提亮，墙柱的纹路也有部分增强，但图片整体色彩不够；MSR算法处理过后，基本细节都有所展现，但产生了“过增强”现象；文献[20]算法处理后整体有所提亮，也凸显了墙壁的部分纹路，但图片上方窗子的颜色没有显现出来；文献[21]算法处理过后，柱子上面的纹路以及窗子上方的颜色都有所增强，但图片整体清晰度不够。本文算法处理过后，柱子、墙壁上的纹路，图片右下方穿着黄色衣服的人清晰可见，且图片上方窗子的颜色更鲜艳了。

2) 客观评价。表1-表2分别是图11、图12所对应的图像质量评价指标表。

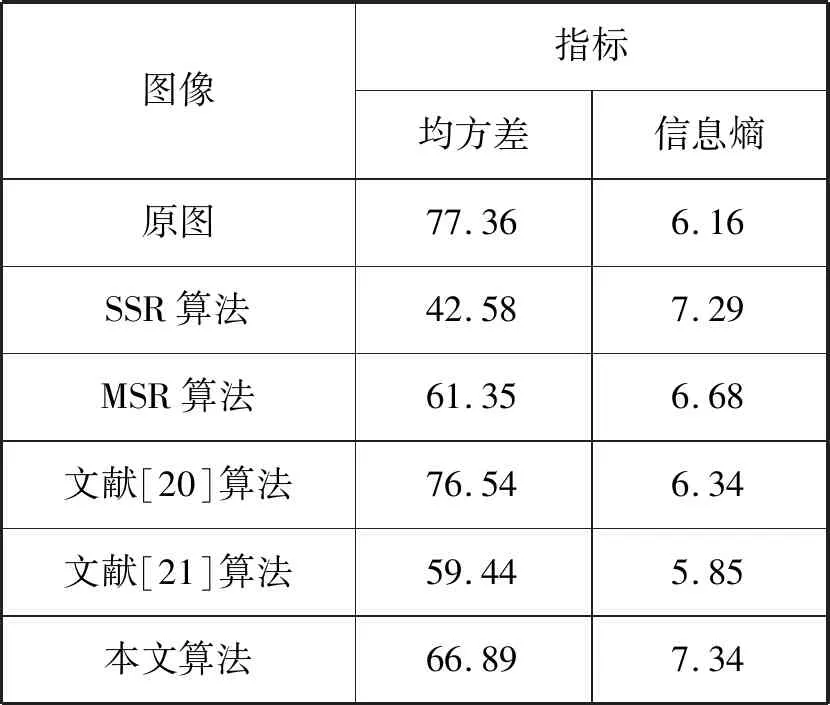
表1 小男孩图的评价指标信息表

表2 教堂内部图的评价指标信息表

分析两个表中的数据可得出：本文算法的均方差数值处于中间，说明图像亮度分布较均匀，色彩较饱满鲜艳，图像整体并不会太亮及太暗；信息熵最大，说明增强后的图像包含的细节信息较多、层次较丰富、轮廓较清晰。

4 结 语

本文在传统的单尺度Retinex算法基础上，进行颜色空间的转换并对相应的分量做处理以及滤波函数的替换。通过对低照度图片进行的实验表明，本文HSV空间的基于BLPF的改进SSR算法在低照度图像清晰化处理方面明显优于传统的SSR算法、MSR算法。本文算法将图片从RGB空间各通道转换到HSV空间各通道，可以解决R、G、B三分量之间因有着较高关联性所导致的颜色失真问题，更符合人类眼中所认知的颜色空间；之后对S分量进行线性拉伸，对V分量进行改进的Retinex增强，可以使得图像细节更为突出，提升图像暗区亮度的同时抑制局部高亮区的“光晕”；最后将图像转回RGB空间各通道，可以使得图像整体层次分明，色彩艳丽，从而达到较好的增强效果。