Geiger型碳纤维索穹顶结构连续倒塌性能非线性分析
惠 卓,秦卫红,许剑武,张 普,张同庆,解 鹏,张润蕾
(1.东南大学 混凝土及预应力混凝土结构教育部重点实验室,南京 211189;2.东南大学 国家预应力工程技术研究中心,南京 211189;3.郑州大学 土木工程学院,郑州 450001)
随着我国经济的不断发展,大跨空间结构广泛应用于体育馆、商场、会议中心等公共建筑。索穹顶是一种受力合理、结构效率高的新型大跨空间结构体系,该体系一经问世,便因其创新的造型、独特的构造、自重轻等优点赢得了工程师们的青睐。同时,碳纤维材料具有轻质高强、耐久性好、耐疲劳性能优良的优点。将碳纤维应用于索穹顶的拉索上,材料和结构优势相结合,在超大跨度空间结构中将会有良好的应用前景。
目前,空间结构的抗连续倒塌研究主要集中于网架和网壳结构,预应力空间结构的研究较少,尤其缺乏索穹顶结构的相关研究。郑君华[1]、陈联盟[2]分别对Levy型和Kiewitt型索穹顶进行了局部索杆破断分析,得出索的破坏都将对结构的刚度产生很大影响,部分索破断将使结构成为机构,不能继续承受荷载。何键等[3]通过观察局部索(杆)破坏是否引起其它索杆的强度破坏来判断结构是否连续倒塌,同时区分了不同位置杆件的安全等级。钟凌等[4]对葵花型索穹顶试验模型进行竖向对称加载、非对称加载以及拉索瞬间破断试验。陆金钰等[5]提出一种新型的环箍穹顶全张力自平衡索杆结构,分析模拟了环形张拉整体不同部位的拉索断裂后剩余结构的响应。
上述研究集中于非Geiger型索穹顶的断索研究,有关Geiger型索穹顶的连续倒塌动力非线性分析非常少见,这是因为该结构本身的几何构成特点导致单根构件失效后结构的响应过大,存在部分结构因位移过大而无法模拟倒塌全过程的现象。
所以本文选取一跨度为100 m、矢跨比为0.1的Geiger型碳纤维索穹顶结构进行了连续倒塌仿真分析,研究不同构件失效后结构的连续倒塌特点,分析结构的内力重分布过程。
1 索穹顶结构连续倒塌分析方法
1.1 倒塌分析方法
现有国内外规范[6-9]中涉及结构抗连续倒塌能力的设计方法主要分为四种:概念设计法、拉结强度设计法、拆除构件设计法、关键构件设计法。其中,采用最多的是拆除构件设计法。拆除构件设计法又称备用传力路径AP方法。该方法是将结构中的部分构件拆除,模仿局部初始破坏,通过分析剩余结构的力学响应,来评估判断结构是否会发生连续倒塌。拆除构件法根据是否考虑非线性和动力效应,可以分为线性静力、线性动力、非线性静力和非线性动力拆除四种方法。本文采用非线性动力拆除构件法。
目前国内外主要利用ANSYS等隐式分析软件对结构进行连续倒塌仿真分析,但对于Geiger型索穹顶,由于其上弦各榀桁架之间沿环向联系较少,单根构件失效后结构的响应过大,各类隐式分析软件难以计算分析其连续倒塌全过程。因此本文综合运用ANSYS和LS-DYNA针对Geiger型碳纤维索穹顶结构进行连续倒塌非线性动力分析。
1.2 等效荷载瞬时卸载法
目前模拟拆除初始失效构件后引起的动力效应的方法[10-13]有瞬时加载法、初始条件法、等效荷载瞬时卸载法。本文采用等效荷载瞬时卸载法。图1为该方法的示意图。
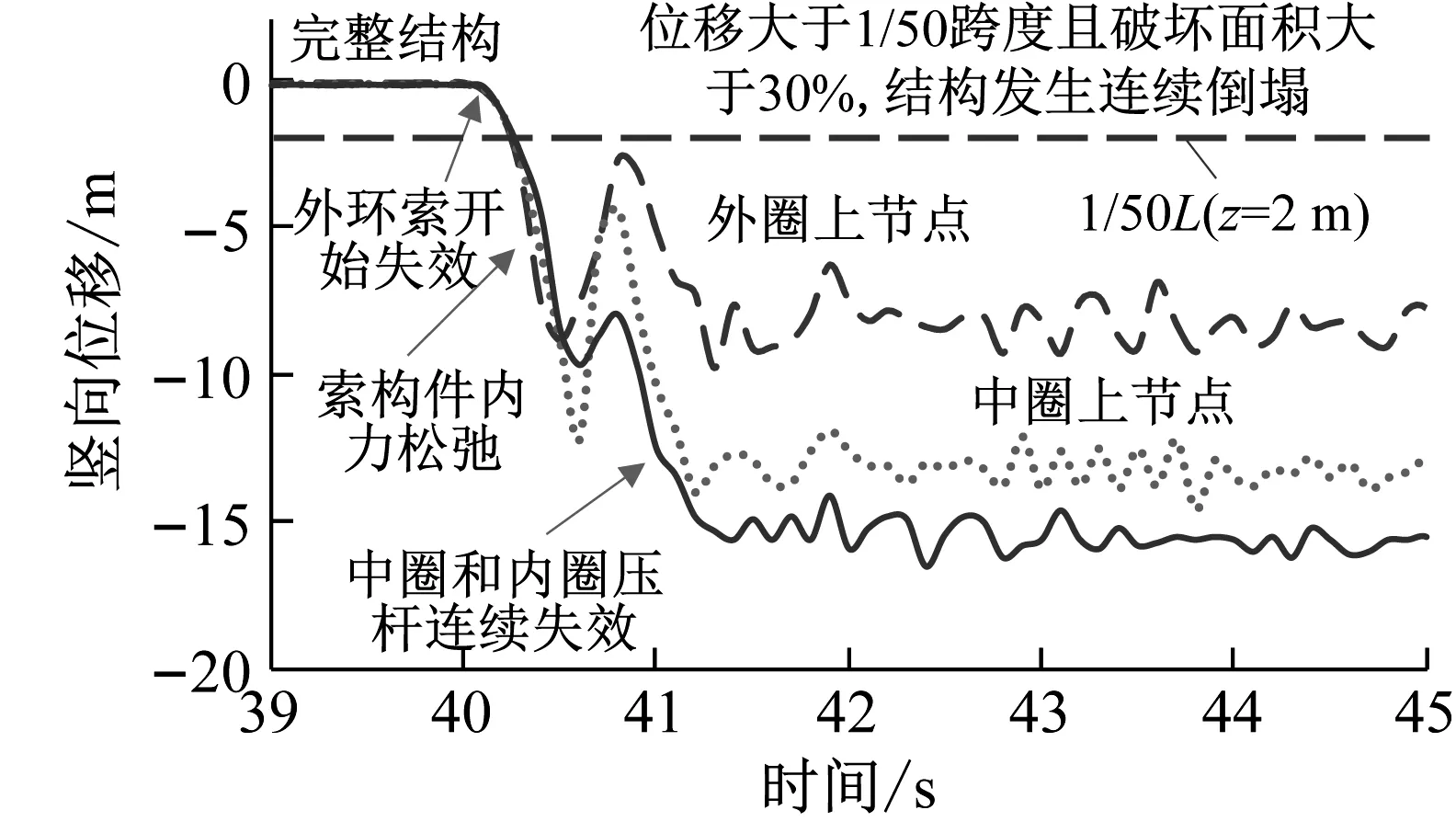
如图1所示,LS-DYNA中拆除某构件时结构的动力响应分为三个阶段(图1(a)):①t=0为初始阶段,即索穹顶结构完整的时刻(图1(b))。② 0 图1 等效荷载瞬时卸载法示意图 合理的倒塌破坏准则是连续倒塌分析的关键。破坏准则按层次[14]分为:材料层次、构件层次、结构层次。按类型分为:强度准则、变形准则、机构准则、稳定准则、疲劳破坏准则、能量准则。 本文中,构件和材料层次破坏准则定义为:强度准则和应变准则。拉索采用强度准则,当拉索强度超过极限抗拉强度时判定索失效。而压杆采用应变准则,因为结构的连续倒塌是一个高应变速率的非线性动力冲击过程,目前暂未有明确的的失效应变取值,本文参考文献[15],取压杆失效应变为0.01。当压杆应变达到0.01时判定压杆失效。 结构层次破坏准则。本文参考美国规范UFC4-023-03[9]定义结构层次破坏准则:①当索穹顶最大的节点竖向位移大于跨度的1/50且失效面积达到结构总平面面积的30%时,认为结构生连续倒塌破坏;②当索穹顶最大的竖向节点位移大于跨度的1/50、但失效面积未达到结构总平面面积的30%时,认为结构发生局部连续倒塌破坏;③当索穹顶最大的竖向节点位移小于跨度的1/50时,或当索穹顶最大的节点位移大于跨度的1/50、但失效面积未达到结构总平面面积的15%时,认为结构未发生连续倒塌破坏。 图2为环向12等分的Geiger型碳纤维索穹顶结构模型。结构由13组构件组成,每组各有12个同类构件。构件的具体规格参数见表1。 (a)轴测图 表1 索穹顶构件规格和初始预应力 拉索采用碳纤维材料。考虑到目前碳纤维压杆的失稳和失效模式少见成熟的研究结果,所以本文设计的碳纤维索穹顶结构的压杆仍然采用Q345级钢材。构件材料参数见表2。考虑拉索的疲劳因素,由相关规范[16]和文献[17]可知,拉索在常规荷载作用下的应力取值控制在0.4fptk以内,故本文将拉索受荷前的初始预应力控制在(0.25~0.35)fptk。最大位移限值:在正常使用极限状态下,结构最大的挠度不得大于跨度的1/250。 表2 材料参数表 考虑到索穹顶结构的屋面膜材刚度比较小,在本文中忽略膜面刚度影响,将膜上的荷载等效为压杆上节点荷载考虑,同时将构件的密度放大1.2倍以计入节点本身的重量。根据GB 50009—2012《建筑结构荷载规范》[18]及CECS 158—2015《膜结构技术规程》[19],屋面恒荷载取0.15 kN/m2(包括膜和灯具等自重),活荷载取0.3 kN/m2。在连续倒塌非线性动力分析中,参考规范[9],采用的连续倒塌分析所用的荷载工况组合为:1.2×恒载+0.5×活载。 在分析中,相比于钢索穹顶,碳纤维索穹顶主要有以下三点不同:①阻尼比更大,振动中更容易稳定;②自重轻,但是刚度小,因此需要权衡应力比和位移限制;③自振周期小。考虑上述因素,图1中的等效荷载替换时间和构件失效时间比全钢索穹顶的时间短。较短拆除时间,导致其结构的响应比钢索穹顶更大。 在ANSYS/LS-DYNAY有限元软件建模时,索简化为铰接的只受拉不受压单元,采用LINK167单元模拟;采用Cable材料模型,通过定义索的偏置量来施加索的预应力。 压杆采用两端铰接的梁单元BEAM161;采用Plastic Kinematic材料模型。该单元可以模拟压杆屈曲失稳。本文采用失效应变来控制杆单元的生死,当结构中单元应变超过失效应变时,单元自动从模型中删除,刚度贡献为零。如前所述,失效应变取0.01。 结构支座按铰接处理。分析时不考虑索穹顶与外环梁和下部结构的相互作用。 本节研究不同部位构件初始失效之后结构的动力响应过程和最终倒塌状态。由于篇幅限制,仅列举1根外环索失效后结构的破坏过程,代表了发生整体连续倒塌的拆除过程,其余构件失效工况采用列表方式汇总并进行对比分析。 3.1.1 倒塌过程 采用等效荷载瞬时卸载法(图1所示)模拟拆除单根外环索,此拆除工况下结构发生连续倒塌。倒塌过程各阶段如图3所示。 由图3(a)可以看出,t=40 s时,结构处于拆除前的相对稳定状态。随后的0.2 s内,外环索失效。 (a)t=40 s时,外环索刚开始失效 t=40.4 s时,结构发生剧烈振荡和内力重分布,此时最大竖向位移超过跨度的1/50。外环索和斜索全部松弛,导致相连外压杆倾斜并发生轴压力卸载。但是其余压杆由于处于传力路径上,轴力增大。内圈压杆因设计截面小,先发生屈曲,随后中圈压杆轴力增大也屈曲。 t=40.6 s时,与初始失效环索相邻的中圈和内圈压杆达到0.01的失效应变,其他压杆依次由近向远屈曲直至破坏失效,造成中圈脊索和斜索内力全部松弛,随后靠近初始失效处外圈压杆破坏失效。 上述“屈曲”和“失效”对应压杆的两个关键受力状态。屈曲状态为压杆达到极值点失稳。失效状态为杆件达到极值点失稳之后发生卸载,直至极限应变达到0.01。“失效”之后,压杆对结构的刚度贡献完全消失。 t=60 s时,在阻尼的耗能作用下结构振动基本稳定,完成内力重分布。整个结构完全倒塌,全部索构件松弛。 图4所示的数字为压杆失效顺序。由图可见,与拆除的外环索临近的几榀中圈压杆第一批失效。然后,遵循着由近及远的顺序,通过内圈压杆向远离初始拆除外环索的另外半跨的中圈压杆传递,具体见图上的虚线箭头。 图4 压杆破坏失效顺序 最终,参见1.3节结构破坏准则:节点最大竖向位移大于跨度的1/50,且失效面积超过结构总平面面积的30%。故判定该拆除环索工况时结构发生整体连续倒塌破坏。 3.1.2 节点位移和构件内力响应 图5(a)列出距初始失效外环索最近榀的外圈、中圈和内圈上节点的位移时程曲线。 由图5(a)可见,外环索失效导致内圈、中圈和外圈节点的竖向位移急剧增大,各圈位移最终均超过跨度的1/50,其中最大竖向位移发生在内圈节点。产生该现象的原因为单根外环索失效后使大量索构件内力松弛、中圈和内圈各根压杆相继失效导致结构完全倒塌。 (a)位移时程图 图5(b)为与初始失效外环索相连各构件的内力时程图。由图5(b)可见,当单根外环索失效后,与其相连的外斜索和外环索立刻松弛,稳定后内力接近于零。与失效外环索相连的外压杆也发生屈曲、最终失效,稳定后内力也接近于零。 3.1.3 各类构件的内力响应系数 图6为构件i在构件j拆除前、拆除时和拆除后的内力响应时程曲线。 图6中,Ni为第i构件的初始内力;Njimax、Nji分别为j构件失效后i构件动力响应中的最大内力、振动稳定后的最终内力。 图6 构件j拆除前、后第i构件的内力时程图 为了评估结构的抗连续倒塌性能,现定义最大内力响应系数Rji和稳定内力响应系数Sji,如式(1)和式(2)所示: Rji=Njimax/Ni (1) Sji=Nji/Ni (2) 式中:Rji为j构件失效后i构件最大内力响应系数;Sji为j构件失效后i构件稳定内力响应系数。上述内力均取绝对值。 表3列出拆除单根外环索后,索穹顶各类构件的最大和稳定内力响应系数。 表3 拆除外环索后构件最大和稳定内力响应系数 由表3可见,单根外环索拆除后,外环索和外斜索最大内力响应系数均小于1,稳定内力响应系数均为零左右。原因分析如下:①一根外环索拆除后,整圈外环索传力路径突然中断,各外环索相继发生松弛,振动稳定之后最终完全卸载。所以各榀外环索的最大动力响应均小于环索的初始内力,稳定之后内力均卸载为零。②各榀外环索松弛、卸载之后,与之相连的外斜索也发生了松弛和卸载。 其余构件最大内力响应系数都大于1。说明外环索传力路径中断后,在中圈和内圈的索和压杆以及外圈的压杆产生了替代传力路径。在结构激烈振动期,这些构件的瞬间最大内力均大于拆除前的初始内力。 除脊索和上环索之外,其他构件稳定内力响应系数基本为零。原因分析如下:结构的外荷载均施加在上节点处。当结构整体塌陷后,压杆大多数已经破坏失效、或者倾斜。荷载无法由上节点通过压杆传递到下节点,所以与下节点相连的环索、斜索和压杆在结构振动稳定后几乎不受力。整个结构只有上部的各圈脊索和环索像松弛的绳子一样承担外荷载。拆除构件之前各构件张拉的预应力及其产生的结构应力刚度几乎完全消失,结构完全倒塌。 由上节可知,构件的稳定内力响应系数与结构倒塌与否存在很大相关性。该系数越小,说明构件松弛程度越大,松弛后该构件所提供的应力刚度越小。然而单根构件的稳定内力响应系数Sji仅能反映j构件失效后一根i构件的内力变化,而无法描述j构件失效后对整个结构的影响程度。为了描述各初始失效构件拆除后对整体结构造成的影响,在稳定内力响应系数的基础上,本文提出结构的重要性矩阵和构件的重要性系数两个概念,具体如式(3)和(4)所示: (3) (4) 式中:[M]为结构的重要性矩阵;mj为构件j的重要性系数;n为构件数量,本文n=156;式中,当i=j时,令:Sij=1。 由式(4)定义可知,构件j的重要性系数mj的取值在0~1之间。若mj越大,则表明该构件失效后其他各构件应力松弛的程度越大,对结构的影响大,容易导致索穹顶结构发生连续倒塌。 依据构件重要性系数,将构件分为三类:①关键构件:即在合理设计下,该类构件初始失效后,结构发生不可避免的连续倒塌;②重要构件:即在合理设计下,该类构件初始失效后,结构发生局部倒塌破坏;③一般构件:该类构件初始失效后,结构不倒塌。 表4中汇总了Geiger型索穹顶13类构件的拆除结果,主要包括倒塌结果、构件类别、重要性系数、压杆失效数量、结构失效顺序和稳定备用路径。 由表4可见:拆除单根各类型环索后,压杆大多数已经破坏失效、或者倾斜,荷载无法由上节点通过压杆传递到下节点,所以与下节点相连的环索、斜索和压杆在结构振动稳定后内力出现较大变化。说明,压杆在索穹顶抗连续倒塌设计中至关重要。 基于构件重要性系数,根据上述表4结果,可以建立如下的倒塌控制方程: 表4 拆除结果汇总 拆除各类构件后,依据式(2),(4)得出各拆除构件的重要性系数,绘制于图7。 图7 构件重要性系数 由图7可见,依据重要性系数及倒塌结果,Geiger型索穹顶构件具体划分为:①关键构件:外环索、中环索;②重要构件:上部内环索、下部内环索、外斜索;③一般构件:脊索、中斜索、内斜索、压杆。拆除关键构件、重要构件和一般构件分别造成索穹顶结构的整体连续倒塌、局部连续倒塌和不连续倒塌。综上,不同圈次位置同类构件的重要性系数基本符合:外圈>中圈>内圈。相同圈次位置不同类构件的重要性系数基本符合:环索>斜索>脊索>压杆。 除关注稳定内力响应系数之外,最大内力响应系数和各拆除工况的备用传力路径相关。因此依据式(1)得出所有拆除工况下同类构件的最大内力响应系数,绘制于图8。 图8 最大内力响应系数 由图8可见:除关键构件之外,其它构件拆除后,索构件的最大内力响应系数大多低于3。故在进行索穹顶结构常规设计时,若保持上述索在常规荷载作用下的应力比小于1/3,则在拆除非关键构件后,索的最大内力响应不会超过其极限强度。上述要求是比较容易达到的。 对于图8中最大内力响应大于3的个别构件,可以通过后述的参数分析进行优化,达到防止最大内力超出索极限强度的目的。 由最大内力响应系数和折线图可以得知,任意构件失效后,同类构件不同圈次位置的最大内力响应系数基本符合:内圈>中圈>外圈。这是因为各构件在常规荷载作用下的初始内力遵循着如下规律:内圈<中圈<外圈,即内圈的内力最小。但是内圈各构件处在必经的替代传力路径上,由其它圈构件传来的动力响应的绝对值与其他圈构件动力响应数值相当。所以各圈的最大内力响应系数遵循如下规律:内圈>中圈>外圈。由此可见,尽管在常规荷载作用下内圈的受力较小,但是从考虑连续倒塌的替代传力路径角度出发,在设计内圈各构件(尤其是内圈压杆)的截面时,宜比其他圈构件的安全储备适当放大。 为研究设计参数变化对碳纤维索穹顶结构抗连续倒塌性能的影响,对上述结构进行参数分析。所选参数为构件初始预应力和截面面积。经分析可知,其中,各参数变化不会改变关键构件拆除工况的倒塌结果,因此本文不再详细描述关键构件拆除工况下的参数分析。而重要构件拆除后的结构倒塌与否受上述参数的影响较为明显,因此下面重点论述参数变化对重要构件拆除工况的影响。在重要构件中,最大内力响应系数出现于下部内环索拆除工况,故下文只选取该拆除工况。 在保持索穹顶其它设计参数不变的情况下,将初始预应力取3组不同初始预应力值,分别为0.67P、1P、1.33P(P为第3节中索穹顶各构件的初始预应力),该三种初始预应力时,结构均满足正常使用阶段的位移限值条件。 图9中列出不同预应力水平下结构内圈上节点位移时程曲线。 图9 不同预应力水平内圈上节点位移时程图 由图9可见:①不同预应力水平时,内圈上节点位移时程曲线具有相同的变化趋势;②初始预应力水平越大,竖向位移越小,这是因为大初始预应力提供了更大的结构应力刚度;③尽管如此,初始预应力大小对单根下部内环索拆除工况的结构最终破坏形态影响并不大,均发生局部倒塌。 在保持索穹顶其它设计参数不变的情况下,增大各构件的截面面积。若A为本文结构构件的截面面积,将各构件按照如下4种方案增大截面面积,分别为1A、1.5A(所有构件截面面积均为原来面积的1.5倍,余同)、2A和1A/2A(下部内环索、内圈和中圈压杆截面面积为2A,其它构件截面面积为1A)。 单根下部内环索失效后,上述4种截面面积方案中,1A和1.5A方案的结构发生局部连续倒塌,而2A和1A/2A方案的结构则未发生连续倒塌。 图10中列出不同截面面积下结构内圈上节点位移时程曲线。 图10 不同截面面积内圈上节点位移时程图 从图10可见:t≤41 s,不同截面面积下内圈上节点位移时程曲线具有相同的变化趋势,但是当t>41 s,与1A、1.5A曲线相比,1A/2A和2A索穹顶结构的位移没有进一步加大,保持了结构的整体稳定性,未发生连续倒塌。 同时,上述未局部倒塌方案中索构件的最大内力响应系数仅为2.65,均小于3,拉索均未达到极限强度。可见,原结构在拆除下部内环索工况时的局部倒塌,可以经过截面面积合理的调整,转变成结构不倒塌。下部内环索由重要构件变为一般构件。 由上述分析结果,结合其它重要构件(限于篇幅,本文不详述)的参数化分析结果可知:造成局部倒塌的拆除重要构件工况,当增大内环索、内圈和中圈压杆三种构件的截面面积,可防止结构的局部连续倒塌。即重要构件可转变为一般构件。可见这三种构件对索穹顶的抗连续倒塌性能有重要意义。产生这种现象的原因在于,由于结构本身的构成特点,这三种构件属于预应力较小的部位。然而在承受外加荷载之后、或者在拆除构件之后,这三种构件的内力增量并不比其他预应力较大部位构件小多少。 综上,针对Geiger型碳纤维索穹顶的初始预应力,提出以下设计建议:内圈和中圈压杆、内圈环索、其他构件的应力比限值依次为0.15、0.20、0.35。采取上述应力比的索穹顶结构,一般可以将发生局部倒塌的拆除工况改善为不倒塌。其中,安全系数大的内圈和中圈压杆、以及内圈环索,由于本身截面面积较小,所以采取上述方案不会造成过大的造价成本增长,同时也大体上满足常规荷载作用下应力比限值≤0.4的要求。 经多次参数变化分析可知,造成连续倒塌的关键构件拆除工况无法通过改变构件截面面积转变为不倒塌或局部倒塌。 采用ANSYS/LS-DYNA有限元软件,基于备用传力路径法(AP法),模拟了分别拆除13种不同种类构件后Geiger型碳纤维索穹顶结构的倒塌过程,得到以下结论。 (1)提出了重要性系数的概念,并建立了倒塌控制方程。依据倒塌控制方程,将构件分为三类:关键构件(拆除该类构件造成结构的整体连续倒塌:外环索、中环索)、重要构件(拆除该类构件造成结构的局部连续倒塌:上部内环索、下部内环索、外斜索)和一般构件(拆除该类构件不会造成结构的连续倒塌:脊索、中斜索、内斜索、压杆)。 (2)相同圈次不同类型构件的重要性系数基本符合如下规律:环索>斜索>脊索>压杆。同类构件不同圈次构件的重要性系数基本符合:外圈构件>中圈构件>内圈构件。 (3)同类构件的最大内力响应系数基本符合:内圈构件>中圈构件>外圈构件;通过参数分析,验证了拆除重要构件工况,可以通过增大并优化构件截面面积达到改变构件倒塌结果的目的。 (4)通过参数分析可知,提高内圈拉索、内圈压杆和中圈压杆的设计富余量,对结构抗连续倒塌性能起着关键作用。因此提出如下设计建议:构件初始预应力的应力比不应超过以下限值:内圈和中圈压杆0.15、内圈环索0.2、其他构件0.35。
1.3 连续倒塌失效评判准则
2 碳纤维索穹顶结构有限元分析模型
2.1 结构模型简介



2.2 单元类型的选取
3 模拟结果及分析
3.1 拆除单根外环索后结构的倒塌过程




3.2 重要性矩阵与倒塌控制方程



4 参数分析
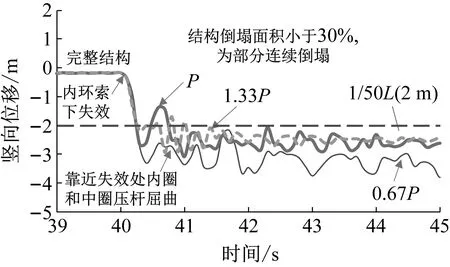
4.1 初始预应力的影响
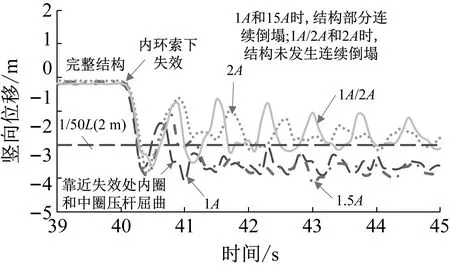
4.2 截面面积的影响
5 结 论

