频谱泄漏校正的多频实信号频率估计算法
陈 鹏,赵少美,陈 钦,解志军,陈晓辉,涂亚庆
(1.中国空气动力研究与发展中心 空气动力学国家重点实验室,四川 绵阳 621000;2.中国空气动力研究与发展中心 设备设计及测试技术研究所,四川 绵阳 621000;3.陆军勤务学院 军事物流系,重庆 401311)
多频信号的频率估计是数字信号处理中一个非常基础但很重要的问题,广泛应用于电力系统、仪器仪表装置、测量以及无损检测等领域[1-2]。例如,线性调频连续波(linear frequency modulation continuous wave, LFMCW)雷达就是通过估计采样信号频率来测量目标距离,频率估计精度直接关系着雷达的测距精度[3]。
根据对信号的不同处理方式,频率估计算法一般可分为时域法和频域法[4-5]。频域法利用DFT(discrete fourier transform)法对信号进行频谱分析,其抗噪性能好、计算速度快,因此得到了学者们更多的关注与研究[6-7]。
多频实信号可理解为含有多个正频率分量和多个对应负频率分量的复信号,在对其进行频谱分析时,频率估计精度同时受所有负频率频谱泄漏和多个待估计正频率频谱间相互泄漏的影响[8]。为抑制频谱泄漏的影响,文献[9-10]利用各类窗函数提高了部分条件下的频率估计精度,但加窗损失了信号能量,且为了追求窗函数性能,设计的窗函数越来越复杂,导致计算量偏大,对算法性能提升不明显,整体效果不佳。针对多频复信号,文献[11]通过频率调制和滤除非待估计频率的方式实现了多频复信号频率估计,后续称为DFE法;文献[12-13]通过频谱泄漏校正提高了频率估计精度,后续称为YA法;文献[14]通过相减策略抑制了频谱泄漏的影响,后续称为CFH法。这三种算法通过不同的方式抑制了多频信号中频谱泄漏的影响,是现有的优秀算法。但在处理多频实信号时,都将多频实信号中的负频率分量看作是独立的频率分量,摒弃了多频实信号中正频率分量和负频率分量的对应关系,导致滤除信号中的负频率成分不彻底,减弱了频谱泄漏抑制能力,特别是在信号频率低、频率间隔近和中高信噪比条件下的频率估计精度较低,有待进一步提高。
为抑制多频实信号中负频率频谱泄漏和正频率频谱间相互泄漏的影响,提高频率估计精度,在分析频谱泄漏影响频率估计原因的基础上,提出了频谱泄漏校正的频率估计算法,并通过仿真实验和实测实验检验了所提算法的有效性和实际应用效果。
1 问题描述
本文以平稳多频实信号为模型进行分析,采样信号如式(1)所示。
n=0,1,…,N-1
(1)
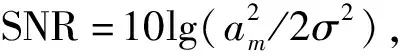
不失一般性,对信号进行频谱分析时,各频率可表示为:
(2)
式中:km=[ωmN/2π]为第m分量频谱最大值索引,[t]表示取最接近于t的整数;-0.5≤δm≤0.5表示第m分量的频谱偏移量。
根据欧拉公式、结合式(2),采样信号可改写为:
(3)
可以看出,多频实信号含有多个正频率分量、多个对应负频率分量和噪声成分。在对第m分量进行频谱分析时,所有负频率频谱、其他非m分量的正频率频谱以及噪声频谱均会产生泄漏,叠加在第m分量正频率频谱上,影响频率估计精度。为直观理解这三者间的相互影响,对单频实信号、多频复信号和多频实信号进行频谱分析,如图1所示。
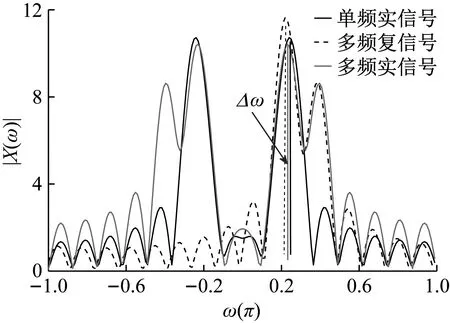
图1 单频实信号、多频复信号和多频实信号频谱
与单频实信号相比,多频实信号不仅受负频率频谱泄漏和噪声的影响,同时还受其他非待估计正频率及其对应负频率频谱泄漏的影响;与多频复信号相比,多频实信号受所有负频率频谱泄漏的影响。因此,对多频实信号进行频率估计时,既要考虑正频率频谱间泄漏的影响,还要考虑所有负频率频谱泄漏的影响,增加了频率估计算法的设计难度。
2 算法流程
为抑制频谱泄漏对多频实信号频率估计精度的影响,提出一种频谱泄漏校正的频率估计算法,旨在提高频率估计精度,特别是在信号频率低、频率间隔近和中高信噪比条件下的估计精度。以下分别从算法思想、算法流程、与YA法对比三方面对所提算法进行介绍。
2.1 算法思想
算法的核心思想是:将多频实信号频谱转换成待估计单频正频率频谱,抑制所有负频率频谱和非待估计正频率频谱泄漏的影响,再对待估计单频正频率频谱进行分析,同时经由迭代计算进一步提高频率估计精度,从而得到各分量精确的频率、幅值和初相位估计值。
算法思想如图2所示,具体流程如下。

图2 算法思想
(1)利用FFT(fast fourier transform)法对采样信号进行预处理,得到各分量准确的频谱索引,并构造所有负频率频谱和非待估计正频率频谱。
(2)采用相减策略,对频谱泄漏进行校正,将采样信号频谱和构造的频谱相减,得到待估计单频正频率频谱。
(3)对待估计单频正频率频谱进行分析,得到较精确的频谱偏移量和复幅值,重新构造所有负频率频谱和非待估计正频率频谱,再进行频谱泄漏校正,通过迭代计算得到各分量精确的参数估计值。
2.2 算法流程
根据算法思想,设计的具体算法流程如下。
首先利用FFT法对采样信号进行预处理,求取信号频谱索引。
(4)
ki=f(Y(k)),i=1,2,…,M
(5)
式中:符号f(t)表示求函数t极大值中最大M个极值的索引,ki表示第i分量的索引。
频谱法具有很强的抗噪性,受噪声影响相对较小,因此设计算法时,为方便公式推导,忽略噪声成分。针对无噪采样信号,对第i分量分析。首先在索引ki两边插值,间隔为0.5,可得到插值点频谱。
(6)

其次通过相减策略,实现频谱泄漏校正。
(7)
然后采用针对单频复信号设计的AM算法[15],对经频谱泄漏校正后的待估计单频正频率频谱进行分析。
(8)
得到频谱偏移量后,利用式(9)求解抑制了频谱泄漏影响的复幅值。
(9)
最后通过迭代计算式(6)~(9),得到每个分量的频谱偏移量和复幅值,从而利用式(2)和式(10)得到各分量精确的频率、幅值和初相位估计值。
(10)
综上分析,算法的具体流程如表1所示。

表1 算法流程
2.3 与YA法对比
为抑制多频复信号中频谱泄漏的影响,文献[12-13]提出了对频谱泄漏进行校正的YA法。所提算法和YA法运用了相似的频谱泄漏校正思路,但两个算法针对的信号模型不同,具体算法步骤有所不同。与YA法相比,所提算法具有两个优势:
(1)多频实信号中正频率分量和负频率分量是对应的,所提算法可确保对应正负频率的绝对值相等,从而保证了频率估计精度。而YA法在处理多频实信号时,将含有M个正频率分量和对应M个负频率分量的多频实信号直接看作是含有2M个独立频率分量的多频复信号,分别估计信号正频率和负频率,摒除了二者之间的对应关系,使得正频率和负频率绝对值之间存在偏差,降低了频率估计精度。
(2)为尽可能地抑制频谱泄漏影响,得到精确的参数估计值,需要在频率估计的基础上,进行幅值和初相位估计,并进行迭代计算。由式(3)可知,对应正负频率分量的幅值相等、初相位大小相等方向相反,所提算法遵循了多频实信号中正频率分量和负频率分量相对应的关系,保证了计算的幅值和初相位是准确的。而YA法摒弃了正负频率间的对应关系,不仅正负频率间存在偏差,在此基础上计算的幅值和初相位也存在偏差,进一步降低了多频实信号的参数估计精度。
所提算法、YA法以及其他现有优秀算法的参数估计性能,将在下一节进行对比分析。
3 性能分析
所提算法属于迭代类算法,算法的计算量是评价算法性能的一个指标。下面,分别从迭代次数和算法复杂度两方面进行分析。
3.1 不同迭代次数
首先在不同迭代次数下进行仿真,分析所提算法的收敛条件。仿真时,设迭代次数为1、2、4和6,SNR=40 dB,结果如图3所示。

图3 不同迭代次数的频率估计结果
经由1次迭代计算,算法的估计效果较差,迭代次数为2时,算法的估计性能得到了提升,但与CRLB仍有很大的偏差。在全频率变化范围内,4次和6次迭代具有相当的估计性能,考虑算法计算量、即算法实时性,后续实验均采用4次迭代计算。
同时,也可以看出,采用4次迭代时,所提算法能够准确地分辨出相差3个频谱间隔(2π/N为一个频谱间隔)的频率分量。当信号的频率分量超过3个频谱间隔后,正频率频谱间的相互泄漏对所提算法的频率估计精度影响非常小。
3.2 算法复杂度
分析算法的计算复杂度时,均省略简单步骤,只统计计算量较大步骤,且将所有复数计算转换为实数计算。对所提算法、DFE法、YA法以及CFH法[14]均取4次迭代计算,统计结果如表2所示。
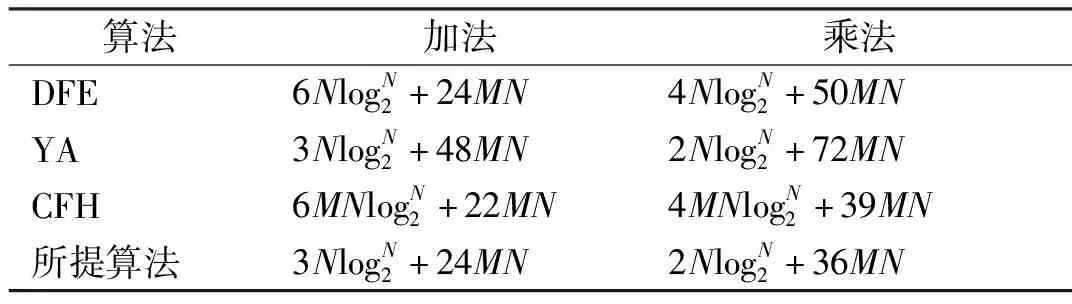
表2 计算复杂度分析

4 仿真验证
为检验所提算法的有效性,利用MATLAB软件在不同条件下,以2个分量的多频实信号为例进行频率估计实验,并与上述算法,以及克拉美罗下限(cramer-rao lower bound,CRLB)[16]进行对比分析。
克拉美罗下限是统计信号的无偏估计下限,常作为算法参数估计精度的检验标准,多频实信号的频率估计下限为:

(11)

(12)
式中:L表示每组实验的计算次数。
4.1 无噪声
经前文分析可知,频域法受频谱泄漏和噪声的影响。因此,在无噪声环境下,可检验各算法的频谱泄漏抑制能力,结果如图4所示。

图4 无噪声条件下的频率估计结果
DFE法、YA法和CFH法分别通过频率调制、频谱泄漏校正和相减策略抑制了频谱泄漏的影响,且频谱泄漏抑制能力逐渐增强。但在处理多频实信号时,这几种算法均将信号中的负频率分量视为独立的复信号,忽略了正负频率分量间的对应关系。所提算法考虑了这之间的对应关系,提升了频谱泄漏抑制能力,强于其他几种算法。
4.2 不同频率间隔
为检验所提算法在不同频率间隔下的频率估计性能,设SNR=30 dB,结果如图5所示。
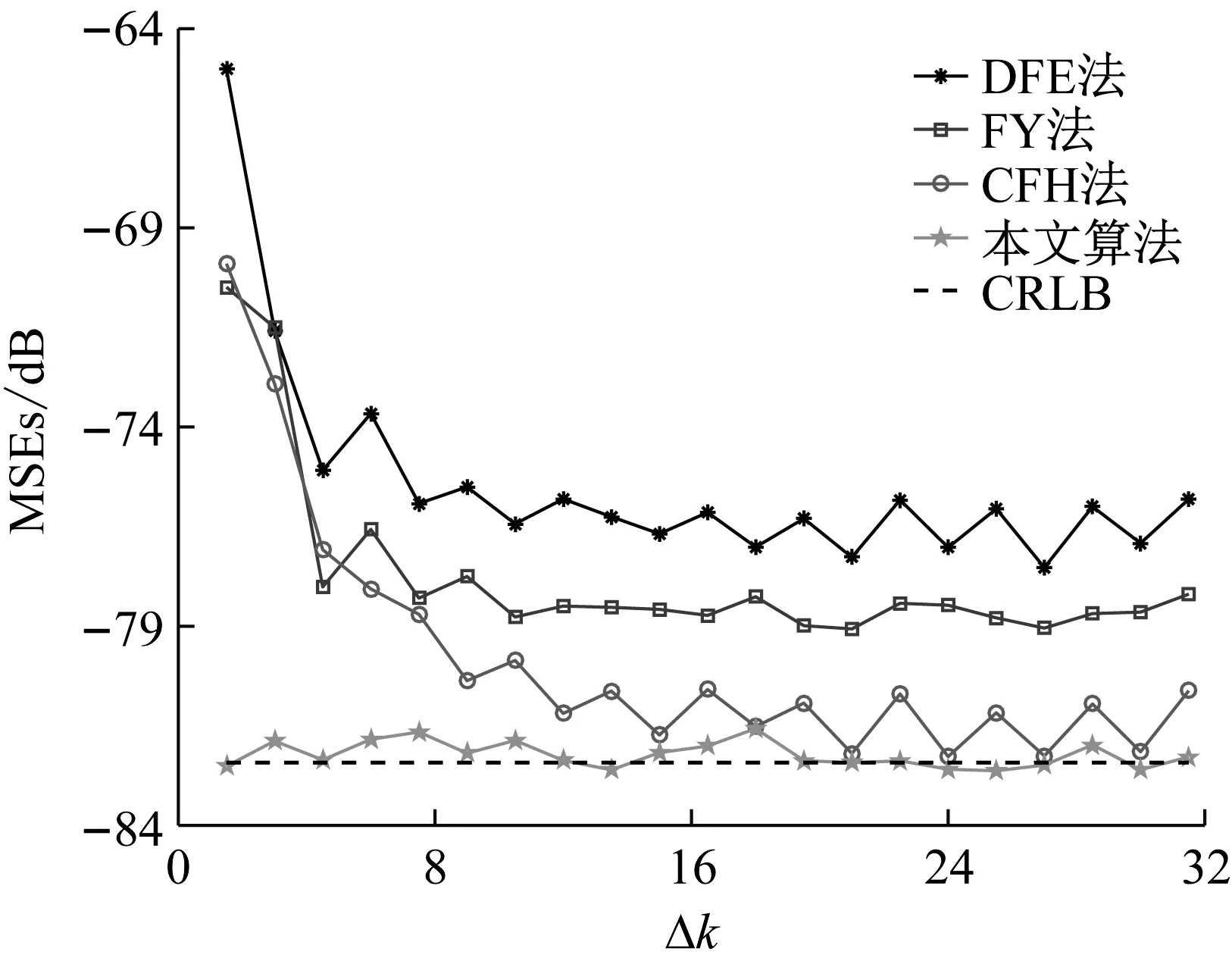
图5 不同频率间隔下的频率估计结果
随着频率分量间隔增加,信号第1分量正频率和对应负频率的影响不变,第2分量正频率和负频率频谱泄漏减少,各算法的频率估计结果逐渐变好。所提算法的频率估计精度优于DFE法、YA法和CFH法,具有更好的频谱泄漏抑制能力,特别是在频率间隔近时的优势更加明显。
4.3 不同频率

图6 不同频率下的频率估计结果
固定频率分量间隔后,改变信号频率就是改变负频率频谱泄漏的影响。随着信号频率增加,负频率频谱泄漏的影响降低,各算法的频率估计精度有所提高。所提算法具有更好的频率估计精度,最靠近CRLB,特别是信号频率较低、负频率频谱泄漏更严重时,优势更加明显。
4.4 不同信噪比
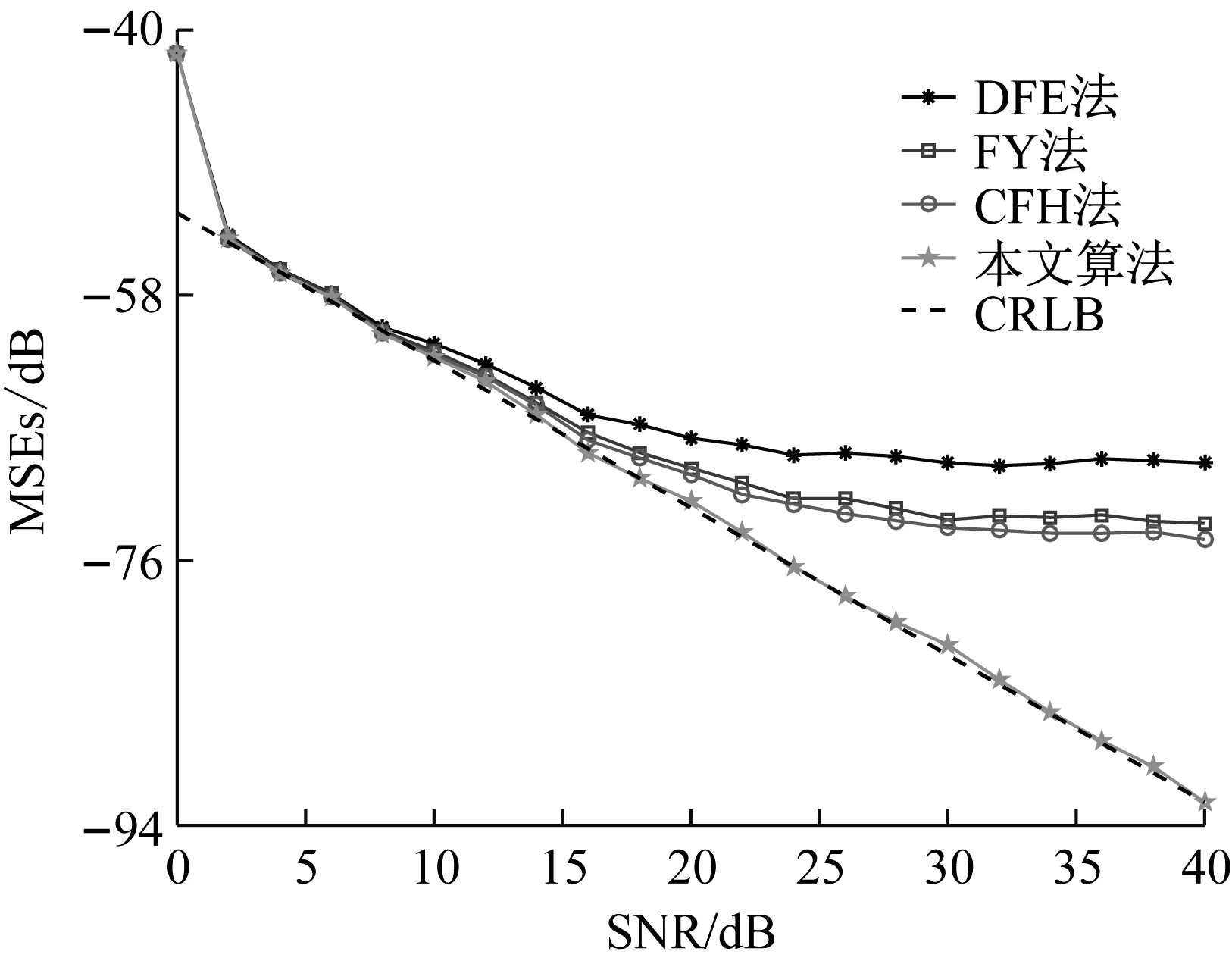
图7 不同信噪比下的频率估计结果
在低信噪比条件下,所选算法具有相当的频率估计精度。随着信噪比逐渐增加,频谱泄漏的影响逐渐加强,DFE法、YA法和CFH法分别逐渐趋于饱和,而所提算法频率估计结果的均方误差一直靠近CRLB,优于其他几种算法,提高了中高信噪比条件下的频率估计精度。
5 实验验证
为检验所提算法的应用效果,利用LFMCW雷达实验平台进行了测距实验,实验现场如图8所示。

图8 测距实验现场
据LFMCW雷达测距原理,测量距离可由下式计算。
(13)
式中:R、fs、C、T、B分别表示测量距离、采样频率、电磁波传播速度、调频周期和调频带宽。
实验时,设锯齿波为调制波,信号中心频率24 GHz,采样频率350 kHz,调频带宽465 MHz,调频周期2 ms,测距范围以1 m的步长从5 m增加到10 m,利用DEVONL80手持激光测距仪和田岛L-50U玻璃纤维标尺来测量实际距离。同时,选用所提算法、YA法和CFH法进行对比,结果如表3所示。

表3 测距结果
所提算法的平均绝对误差为0.038 m,YA法和CFH法的平均绝对误差分别为0.052 m和0.053 m。所提算法的测量结果比YA法和CFH法的测量结果更接近实际距离,算法估计精度与仿真实验结果一致。相比于YA法和CFH法,采用所提算法可改善LFMCW雷达的测距效果。
6 结 论
为抑制多频实信号中负频率频谱泄漏和正频率频谱间相互泄漏的影响,提高信号频率估计精度,提出一种频谱泄漏校正的频率估计算法。该算法通过对信号进行频谱分析,构造所有负频率和正频率插值点频谱,同时通过相减策略抑制了频谱泄漏的影响,校正了待估计正频率频谱,并经迭代计算得到了各分量精确的频率、幅值和初相位估计值。
在不同条件下仿真结果表明,针对多频实信号,特别是在低频或中高信噪比条件下,即负频率频谱泄漏严重时,或者是信号频率间隔较近,即正频率频谱间相互泄漏严重时,所提算法均有效地抑制了频谱泄漏的影响,具有很高的频率估计精度,其频率估计值的均方误差更靠近克拉美罗下限,优于现有的优秀算法。并在LFMCW雷达实验平台进行了测距实验,验证了所提算法的实际应用效果,优于YA法和CFH法。

