地应力测量精度及其全要素量化表征研究

韩晓玉,邬爱清,徐春敏

(长江科学院 水利部岩土力学与工程重点实验室，武汉 430010)

1 研究背景

地应力是地层中未受扰动的天然应力，是地壳应力的统称，是地震预报、采矿、水利水电、土木建筑和交通等地下工程建设的基础资料。天然岩体在特定时空条件下的地应力状态是客观存在的，其数值无法推测，只能通过原地测量确定。美国学者Lieurace于1932年首次进行了原岩应力测量，之后地应力测量方法不断出现，至20世纪90年代，主要测量方法超过10种，测量技术数百种以上[1-2]，之后新方法和技术革新仍不时出现[3-7]。

蔡美峰等[1]将地应力测量方法分为直接法和间接法2类，直接法直接测量各种应力分量并以此计算原岩应力张量，有扁千斤顶法、水压致裂法和声发射法等；间接法测量岩体变形、应变和密度等物理量，依据物理量与应力的关系计算原岩应力，代表性方法为套孔应力解除法。国际岩石力学学会(International Society for Rock Mechanics，ISRM)、美国材料实验协会(American Society for Testing Materials，ASTM)和国内规程均将套孔应力解除法和水压致裂法作为推荐方法[8-12]。前者有孔径变形法和孔壁应变法，代表性元件为美国USBM孔径变形计、南非CSIR三轴应变计和澳大利亚CSIRO空心包体应变计，后者起源于20世纪60年代，是世界范围内应用最广泛的测量方法。

目前，川藏铁路等埋深大、地质条件复杂的工程建设对地应力测量工作提出了高要求，但表征地应力测量准确度的测量精度存在以下问题：

(1)测量技术的测量精度无权威答案，存在孔壁应变测量结果被质疑、水压致裂测量结果计算有争议[13]和新方法、新技术准确度无法衡量的情况。同时，第三方实验室仅能对采集设备和传感器件等元器件进行检定,无法给出测量全过程的测量精度。

(2)地应力测量结果的精度评价由测量过程的误差分析、多方法测量结果对比和地应力场回归分析结果对比等方法给出，在无测量精度权威数据、天然岩体应力测量影响因素多和数值模拟可靠程度低的情况下，上述精度评价具有较大的不确定性。

上述问题存在的原因在于：①地应力测量和地应力测量精度无明确定义，行业内缺乏统一、明确的测量精度表征体系；②测量岩体不符合测量方法的原理设定且无修正技术导致了较大测量误差；③同一个测量方法不同组织的技术方案和测量误差水平参差不齐。对此，本文在已有研究基础上[14-15]提出了闭环概念的地应力测量精度定义和表征体系建议，给出了全要素测量精度表征指标和计算公式，利用公开资料对测量精度表征过程进行了展示。

2 地应力测量精度概念及其研究现状

测量是指为确定被测对象的值而进行试验的过程，测量精度是指反映测量结果与真值接近程度的量。基于上述概念，地应力测量是将测量岩体的初始应力状态作为被测对象并作为测量的初始“输入”(真值)，由测量程序和试验操作实现信号输出和采集，再经辅助试验和结果计算等程序得到“测量结果”(测量值)的过程。对地应力测量过程进行反馈，将“测量结果”与初始“输入”相比较，采用合适的表征指标和计算方法获得二者接近程度的表征，可认为是地应力测量精度的概念。与以岩体作为测量对象的定义不同，上述地应力测量过程和精度概念形成了闭环，是全过程的定义。该定义将地应力测量精度与测量和反馈两过程相关联，并将测量过程所有环节的误差因素和测量岩体的特异影响因素均纳入其研究范畴。特别说明，测量精度是地应力测量准确度的习惯性表述，可进一步引出精密度[16]和正确度概念；测量误差与测量精度意义相对，用来表征“测量值”与“真值”的偏离程度。本文沿用上述习惯性表述，应用中从误差角度反映“测量精度”。

基于上述定义和分析，地应力测量精度研究可分为3个层面：①测量原理及其适用性研究；②测量技术(含设备)及其革新的准确性评价；③特殊岩体测量的修正技术研究。上述层面划分有从测量原理、测量技术和特异岩体测量的技术修正等各个层面进行准确测量研究的涵义。在测量方法确立后，主要是后两个层面的研究，其中套孔应力解除法的研究[1]有：Merrill等对USBM孔径变形计测量技术进行了精度试验，认为其测量误差在5%以内；Hoskings等根据10 a现场测量资料得出USBM孔径变形计的测量误差在应力量值上为20%～100%，在方向上为10%～25%；Leeman等对CSIR应变计进行了精度测量；Worotnicki等对CSIRO空心包体应变计进行了精度试验;蔡美峰[17]提出了地应力测量可靠性等概念，进行了模拟试验，采用量值“比较系数”方式对试验技术的测量精度进行了表征;李远等[7]和乔兰等[18]在提高空心包体测量精度方面进行了持续研究。水压致裂法方面，Fairhurst[19]和Haimson[20]确立和发展了该测量方法;刘建中等[21]进行了多次物理模拟试验研究;刘允芳[22]对测量理论、结果的校核和修正进行了研究;王成虎等[23]针对水压致裂系统柔度对测量结果的影响进行了研究;Frash等[24]研发了真三轴可加热水压致裂装置，对干热岩体的水力压裂特性进行了研究;尹光志等[25]利用真三轴流固耦合试验系统进行了煤岩体的真三轴水力压裂试验。

前述引文涵盖了地应力测量精度3个层面的研究，但未明确给出地应力测量精度的定义、全要素的表征方法和权威数据。对此，需要建立全要素地应力测量精度量化表征体系，其构成应包含3个部分：①统一的测量精度量化表征方法；②合适的试验条件；③测量精度试验实施方案。其中第①部分是基础，后两部分是测量精度表征所需要的“硬件”和“软件”。在上述基础上可形成2个层次体系并发挥相应作用：①权威数据发布体系，该体系可由多个实验室或技术检定实验室组成，程序和数据处理可参考国家标准《测量方法与结果的准确度(正确度与精密度)》(GB/T 6379—2004)[16](等同ISO 5725标准族)，该体系可给出试验技术测量精度的权威数据;②独立运行的地应力测量精度评价实验室体系。

上述表征体系的建立和运行可给出测量技术测量精度的量化指标，进行测量技术测量精度权威数据的检定和发布。此外，测量精度的量化数据是进行特异岩体技术修正方案研究、指导现场测量结果的误差评估、对测量技术革新方案进行测量准确性评价的依据，测量技术的测量精度试验及其数据的广泛评定可推动地应力测量方法和技术的优胜劣汰。

应该说明，地应力行业内有混淆代表性元件、测量技术和测量方法名称的现象，本文对此进行了定义和区分。地应力测量方法是指采用某测量原理进行地应力测量的方法，方法间存在原理差异。地应力测量技术是指基于某测量方法、可实现测量的整个体系，包括由测量程序、技术标准、计算方法等组成的技术方案和测量设备，代表性元件仅为测量设备的主要组成部分。相同测量方法、不同组织的测量技术在测量设备和技术方案不同的情况下存在测量精度差异。测量方法的测量精度可由一段时期内其主流技术的测量精度来代表。此外，部分方法测量过程有人工数据判读环节，该现象增加了测量结果的不确定性并对测量精度评价产生影响，但随着AI等技术的应用，人工判读环节会逐渐减少直至消失。

3 全要素地应力测量精度的量化表征

地应力测量精度的量化表征是在已知初始应力状态和测量结果基础上的结果比较及量化指标提出，现有表征指标只有量值“比较系数”，无单一指标。岩体的地应力状态为三维空间的二阶张量，其结果比较只能在应力量值和角度分量间进行。全要素测量精度量化表征的思路及安排如下：地应力的初始状态或测量结果一般采用二维或者三维正交坐标系的应力量值和角度分量进行表达，一为轴向应力分量和剪应力分量方式，二为主应力量值和主应力角度方式。由于剪应力分量难以施加和测量，因此可利用后一种表达方式进行精度表征，即将二维应力测量的主应力量值和角度、三维应力测量的主应力量值、主应力方位角和倾角作对比项并给出定量指标结果。这种受测量岩体和测量过程全部误差因素影响、针对所有测量结果分量的量化表征称为测量精度的全要素量化表征，其单一指标反映了测量的总体精度或误差。

图1展示了一种授权发明专利提供的套孔应力解除法模拟试验装置[26]，主要包括试验台、试验模型、三维预应力加载装置、用于解除试验的钻机及附属设备、应力测试元件和试验仪器等。上述装置在替换部分试验设备后可实现水压致裂法等钻孔地应力试验方法的模拟和测量精度评价。利用图1的试验条件,在三维加载后进行全过程模拟试验可获得测量结果，采用下述方法可实现其测量精度的量化表征，其中坐标系设定如图2所示。

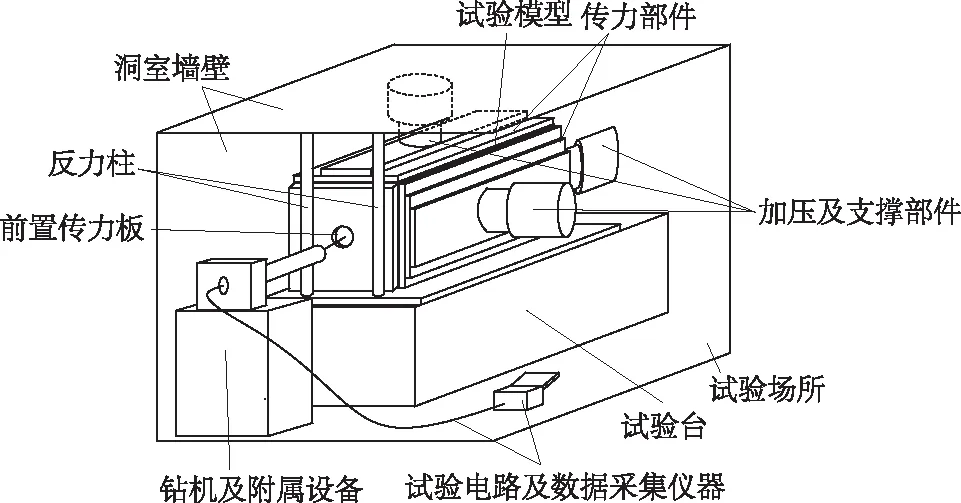
图1 应力解除法三维物理模型试验结构示意图Fig.1 Schematic diagram of 3D physical model test device of overcoring method

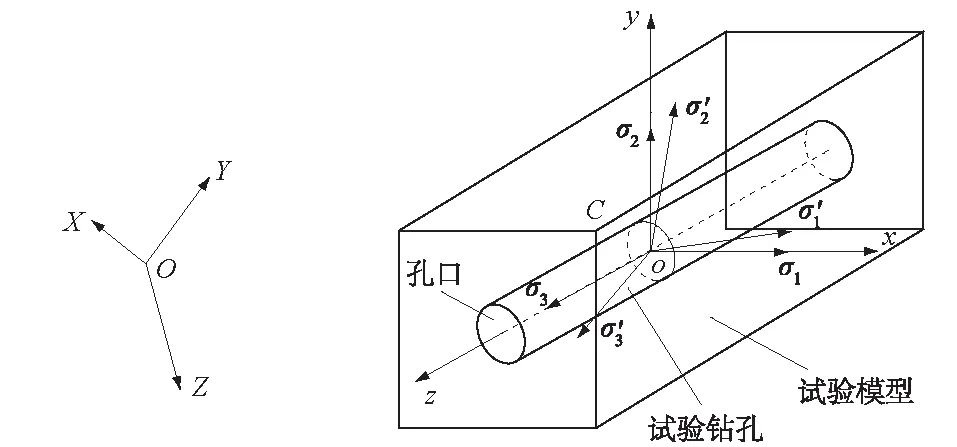
图2 测量精度表征坐标系示意图Fig.2 Coordinate system of measurement accuracy characterization

图2所示O-XYZ为大地坐标系，XY平面为水平面，X轴为正北向，Y轴为正东向，Z轴垂直向下，为了方便模型摆放将大地坐标系进行了旋转。为了方便表述，规定地应力“真值”的主应力量值分别为σ1、σ2和σ3；倾角和方位角分别为α1、α2、α3和β1、β2、β3，其中倾角取值范围为±90°，下倾为正。测量值即模拟结果的主应力计算值用“′”符号加以区分，设试验结果的主应力量值分别为σ1′、σ2′和σ3′，倾角分别为α1′、α2′和α3′，方位角分别为β1′、β2′和β3′。二维应力量值的大、小主应力校验结果分别为σ1′和σ2′，角度分别为α1′和α2′。

为了不出现垂直向(Z向)主应力方位角无法校验的情况，可使得试验加载方向与大地坐标系轴有较大夹角，建议调整后的钻孔坐标系o-xyz的z轴从孔底指向孔口，倾角-45°，方位角135°，等同倾角和方位角分别为45°和315°；x轴正向为水平向(倾角为0°)，方位角N45°E；y轴垂直xz平面斜向上，倾角和方位角分别为-45°和315°，等同倾角45°和方位角135°。

在上述设定下，三维地应力测量精度表征程序如下：①在原坐标系下获得测量结果；②对加载应力和测量结果进行钻孔坐标系转换；③计算大地坐标系下的主应力量值和角度；④计算测量精度。二维测量技术的测量精度表征只须校验“测量平面”的应力和角度。单次试验的应力量值误差由式(1)给出，二维和三维应力的角度误差分别由式(2)和式(3)给出，式(4)为“平均方式”的单一表征指标公式，式(5)和式(6)分别为二维测试和三维测试的“最大值方式”单一表征指标公式。

(1)

(2)

(3)

(4)

εmax=max{δ1,δ2,ζ1,ζ2} ,

(5)

εmax=max{δ1,δ2,δ3,ξ1,ξ2,ξ3,ζ1,ζ2,ζ3} 。(6)

表1 USBM孔径变形计测量精度表征结果Table 1 Characterization result of measurement accuracy of USBM borehole deformation gauge

表2 CSIRO空心包体应变计测量弹性试验材料的结果Table 2 Measurement results of CSIRO hollow inclusion strain gauge in testing elastic materials

表3 CSIRO空心包体应变计测量精度表征结果Table 3 Characterization result of measurement accuracy of CSIRO hollow inclusion strain gauge

4 测量精度表征应用示例

20世纪90年代，蔡美峰等[1]对USBM孔径变形计、CSIR三轴孔壁应变计、CSIRO空心包体应变计和澳大利亚UNSW实心包体应变计进行了多组物理模型试验。试验人员制作了二维加载应力解除试验装置，对试块尺寸效应、材料特性和围压试验的结果应用进行了论证或试验验证。试验材料采用砂岩、大理岩、水泥和混凝土等，实现了对各向异性、均质和不连续介质等材料的模拟。该项试验是迄今为止地应力行业最大规模的套孔应力解除法测量技术精度试验，取得了丰富的成果，获得了主应力量值“比较系数”表征的测量精度数据，验证了非连续、非均质岩体对地应力测量的影响及修正方法，推动了空心包体解除法测量技术的持续革新[1,7,27]。

本文对USBM孔径变形计和CSIRO空心包体应变计的弹性材料试验结果进行了测量精度表征，获得了试验技术的测量精度数据。试验基本情况和表征结果见表1至表3。图3为“比较系数”指标和本文所论述测量精度指标的对比。该项试验技术组成主要包括：1990年代的USBM孔径变形计和CSIRO空心包体应变计；前者试验材料为砂岩、大理岩和水泥，其中3#和5#试验按照各向异性岩体平面应力场公式进行了重新计算；后者的试验材料为混凝土和水泥，其中6#和7#试验材料分别为粗粒和细粒卵石混凝土，该试验材料与线弹性材料水泥试验结果基本一致,具有代表性。此外，USBM孔径变形计采集电路为惠斯通全桥线路，具有温度补偿功能；CSIRO空心包体应变计采用“完全温度补偿”技术；应变计手动安装，角度精度为5°。

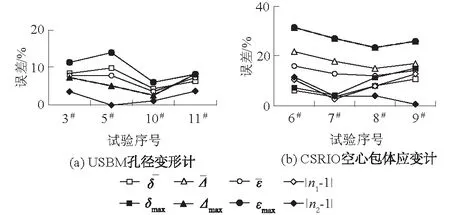
图3 测量精度表征结果比较Fig.3 Comparison of characterization result of mea- surement accuracy between USBM deformation gauge and CSRIO hollow inclusion strain gauge

试验初始钻孔坐标系为O-x0y0z0，x0和y0为水平向，z0垂直向上，右手系。二维正应力加载方向分别为x0向和y0向，大小分别为σx和σy。USBM孔径变形计试验中σx和σy分别等同主应力σ1和σ2，α为第一测量臂到x0轴的夹角。该试验测量精度的量值误差由测量结果的主应力量值和同向加载应力对比得到，角度误差为安装角度α和计算角度α′的误差。CSIRO应变计精度表征首先将初始的测量结果转换为o-xyz坐标系下的测量结果，再计算其大地坐标系下的主应力量值和方向，最后进行主应力量值、方向的相对误差和测量精度计算，上述过程的数据见表2和表3。由于模型试验采用二维加载，z轴方向的第三主应力量值“真值”为0，该主应力量值误差未能计算。上述坐标转换使得各主应力方位角真值位于大地坐标系象限中心处，所有角度误差的校验成为可能。

原试验的测量精度评价指标只采用了应力量值的比较系数n，其数值等于加载应力的测量值除以加载值。该评价方式简单明了，但未对测量结果的剪应力和三维测量结果的角度等分量评价。为了与其它误差形式的指标相比较，本文采用n与1差值的绝对值作为对比项，n的下标为加载应力编号。

由表1知：USBM孔径变形计测量“平均方式”的量值误差为4%～10%，“最大值方式”量值误差为6%～14%，角度误差为3%～8%；总体误差采用“比较系数”方式表征的测量误差为0～14%，“平均方式”单一指标的测量误差为4%～8%，“最大值方式”单一指标的测量误差为6%～14%；角度误差与量值误差数值接近，量值误差总体大于角度误差。

由表2和表3知：CSIRO空心包体应变计测量“平均方式”的量值误差为4%～11%，“最大值方式”的量值误差为4%～15%，“平均方式”的角度误差为15%～22%，“最大值方式”的角度误差为23%～31%，角度误差明显大于量值误差；采用“比较系数”方式表征的总体测量误差为1%～11%，“平均方式”单一指标的测量误差为12%～16%，“最大值方式”的测量误差为23%～31%；角度误差明显大于量值误差。

图3和上述分析表明：

(1)全要素测量精度表征结果中含有量值和角度测量误差，其量化指标反映了测量“岩体”和测量全过程在所有误差因素下的测量准确度，该指标较“比较系数”方式更具代表性。

(2)“平均方式”的单一指标有平均测量误差的作用，“最大值方式”单一指标表征的测量误差最大，同等技术指标对试验技术的准确度提出更高的要求。

(3)USBM孔径变形计所用试验技术方案的总体测量误差均值为10%(εmax指标)。

(4)CSIRO空心包体应变计试验技术的总体测量误差均值为27%(εmax指标)，其角度误差明显大于量值误差。其中的角度误差由应变计制作环节应变片的位置误差和应变计安装的角度误差等环节产生，因此，提升相关环节的技术精度可提高总体测量精度。应该指出，CSIRO测量技术和二维试验加载的不匹配造成了第三主应力的角度误差和总体误差明显偏大。

(5)横向对比，USBM孔径变形计试验技术的测量精度高于CSIRO空心包体应变计。

需要说明：①上述模型试验所用技术目前仍有工程应用，新的数字化改进技术已出现，其精度评价可参照上述模拟试验进行，并可用来评估改进效果；②上述模拟试验条件为最大3.2 MPa的二维加载，与当前主流工程岩体的地应力状态不匹配，地应力测量精度评价需要更为先进的试验条件。

5 结 论

(1)川藏铁路等大埋深、地质条件复杂工程的建设对地应力测量工作提出了高要求，地应力测量技术和测量结果评价亟需统一、全要素的测量精度量化表征体系。

(2)地应力测量精度是指由初始应力状态作为“输入”，由测量过程得到“测量结果”，将“测量结果”与初始应力状态相比较、采用合适指标表征二者接近程度的量。

(3)采用物理模拟试验进行测量技术测量精度的表征可用来验证测量原理、研究特异岩体测量技术修正措施，指导现场测量结果误差评估，评价测量准确度和技术改进效果。

(4)全要素地应力测量精度指标由量值和角度误差组成，“平均方式”表征指标有平均各组成误差的特点；“最大值方式”是对实现技术“严格”要求的表征方式，其单一指标最为严格。

(5)应用示例中所用USBM孔径变形计和CSIRO空心包体应变计测量技术εmax指标的总体测量误差均值分别为10%和27%，单就准确度而言前者优于后者。