超长联络通道冻结温度场发展规律及其对隧道变形的影响

陈军浩，陈笔尖，庄 言，王乐潇

(1.福建工程学院 土木工程学院，福州 350108； 2.福建工程学院 地下工程福建省高校重点实验室，福州 350108)

1 研究背景

联络通道作为安全通道是地铁工程建设的重难点之一，具有施工难度大、危险性高等特点。当通道处于透水性强、承载力低的软土及砂土土层时则需要采取加固措施，防止施工过程中因周边土体扰动而产生不利影响。由于冻结法拥有灵活性好、适应性强、污染小、止水效果好及冻土强度高等优点，现已广泛应用于地铁通道的施工建设当中。土体的冻结过程本质上是一个相变过程，通常伴随水分迁移、土体冻胀及热量流失等现象发生[1]。其中水分迁移与土体冻胀占主导地位，因此研究冻结过程中土体的温度场及位移场发展规律对工程安全控制具有重要意义。

国内外一些学者对地铁联络通道冻结施工案例做了许多研究，如通过研读相关文献对冻结法的应用现状及前景进行概括总结[2]，对地层加固效果进行评价[3]，对强透水、富集海水、白垩系等特殊地层[4-9]的冻结工程进行研究。联络通道冻结法施工主要还是集中于研究冻结过程中温度场及位移场变化规律、冻结壁力学特性及开挖过程中周边结构变化情况等。王晖等[10]通过数值模拟分析了不同工程中联络通道冻结施工过程的变化规律，得到冻土帷幕与隧道管片的接触部位是整个冻土帷幕的薄弱位置，通道及泵站在开挖建造过程中冻土帷幕稳定性将大幅削弱，其中通道顶部沉降量及泵站底部隆起量最大和侧壁连接处是薄弱点；奚守仲等[11]、王彬等[12]分别通过数值分析和理论分析研究了联络通道冻结过程中冻土壁的力学特性及优化设计方法等。陈军浩等[13-15]通过室内冻结模型试验及数值分析研究了冻结管在有无偏斜及不同冻结参数下冻结壁温度场的发展特性，得到多圈管在冻结时，各圈之间容易产生密闭未冻承压水仓且冻结管偏斜对交圈时间及冻结壁径向平均温度影响较大。张松等[16]、姚兆明等[17]通过室内试验分别对地表冻胀量和土体蠕变特性进行研究，为工程应用提供借鉴。

由此可见，现国内外针对联络通道冻结施工问题研究相对较多，但大多集中于短距离联络通道且以二维温度场变化规律研究为主，而对于三维超长联络通道方面研究则较少。本文以福州地铁2号线紫阳—五里亭区间联络通道工程为研究背景，通过对长联络通道冻结温度场进行三维数值仿真及现场实测对比，分析在冻结过程中温度场的变化规律及盾构隧道结构和周边地层在冻胀作用下位移变形的规律,以期为长联络通道冻结施工及设计提供相应的借鉴经验。

2 工程实例

2.1 工程概况

本工程联络通道位于福州地铁2号线紫阳站—五里亭站区间，所处隧道中心间距65.8 m，上覆土层厚度14.7 m。联络通道距最近摩擦型桩6.4 m，且隧道及泵站上方分布众多管线。区间隧道北侧有王庄派出所、农贸市场、公寓等，南侧则有花都集团、福建富士通软件有限公司、行政服务中心等建筑物。

联络通道所处地层自上而下主要为淤泥质粉细砂、淤泥夹砂、(含泥)中细砂、粉质黏土。根据场地钻孔资料，松散岩类孔隙承压水分布于第四系松散沉积物的孔隙中，主要赋存在淤泥中细砂交互层、淤泥质粉细砂、(含泥)中细砂、(含泥)粉细砂、(含泥)粗中砂中。承压水水头较高。各土层中地下水流速缓慢，对土层影响小。

水平联络通道结构采用直墙圆弧拱结构，其初衬(钢支架加木背板)结构厚度为230 mm，二次钢筋混凝土衬砌结构厚度400 mm。通道设计整体开挖轮廓高4.04 m，宽3.76 m。通道相连两盾构隧道直径为6 200 mm，管片厚度350 mm。

2.2 冻结设计

根据工程地质及其他因素条件，确定联络通道采用“隧道内钻凿，布设近水平孔冻结临时加固土体，矿山法暗挖构筑”的施工方案。由于联络通道长达65.8 m，属超长联络通道，为方便钻孔施工及实现更好冻结效果，采用两端均布设冻结管进行水平冻结，冻结孔共设175个，冻结管选用规格Φ108 mm×8 mm，通道处冻结壁设计厚度2 m，通道与盾构隧道交界处除下部设计厚度2 m外，其余为1.7 m，积极冻结时间为50 d，冻土帷幕平均温度应低于-10 ℃。联络通道、隧道及冻结管位置关系如图1所示。

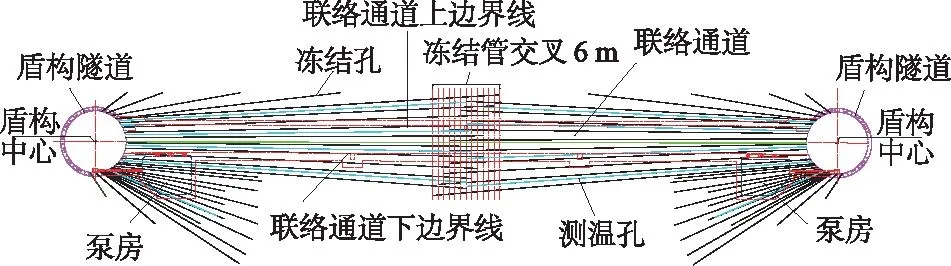
图1 联络通道、隧道及冻结管位置关系Fig.1 Locations of connecting aisle, tunnel and freezing pipes

3 数值分析模型建立

3.1 模型说明

本文采用ANSYS有限元软件对联络通道开挖前的土层冻结进行计算。为提高计算速度，考虑了冻结管布置及盾构隧道分布前后左右近似对称性，建立1/4的分析模型。模型尺寸长55 m×宽15 m×高41.45 m，主要结构包括盾构隧道、冻结管以及冻结加固后拟建的联络通道及泵站，截面尺寸与工程概况保持一致。各结构相对位置如图2所示,图中未显示周边土层。

图2 冻结1/4模型Fig.2 Diagram of 1/4 frozen model

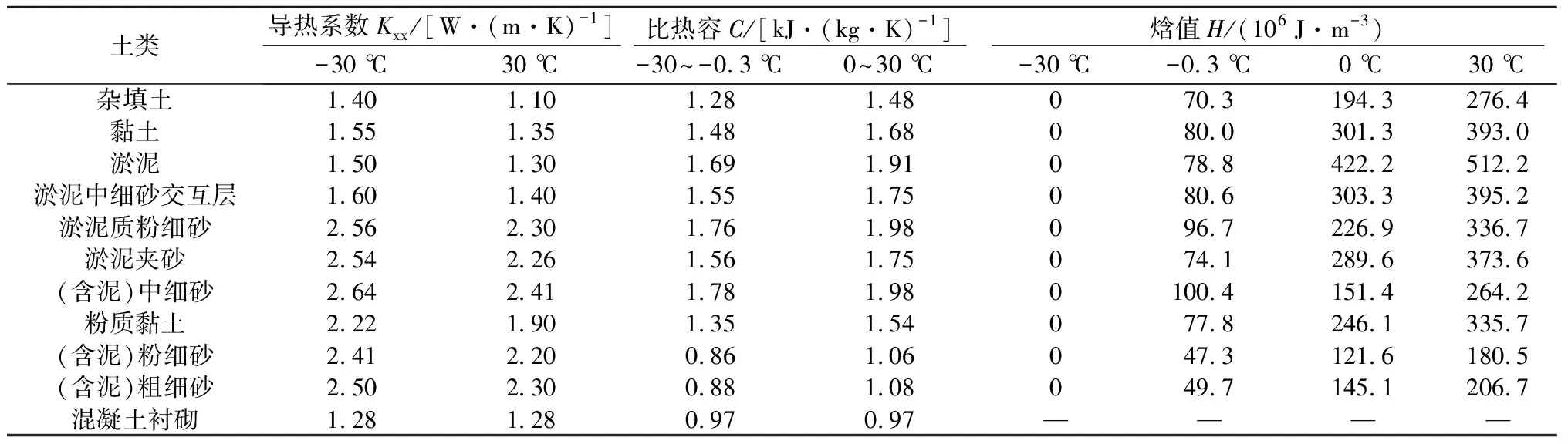
表2 土层热力学参数Table 2 Thermodynamic parameters of soil strata

各土层假定为水平向且各向同性，采用弹性本构模型。为在ANSYS中反映土层性质随温度变化而改变所导致的温度场变化，本文在ANSYS软件中分别选取土层及隧道结构物理力学参数(见表1)、热力学参数(表2)及冻胀系数(表3)(因无实测值，

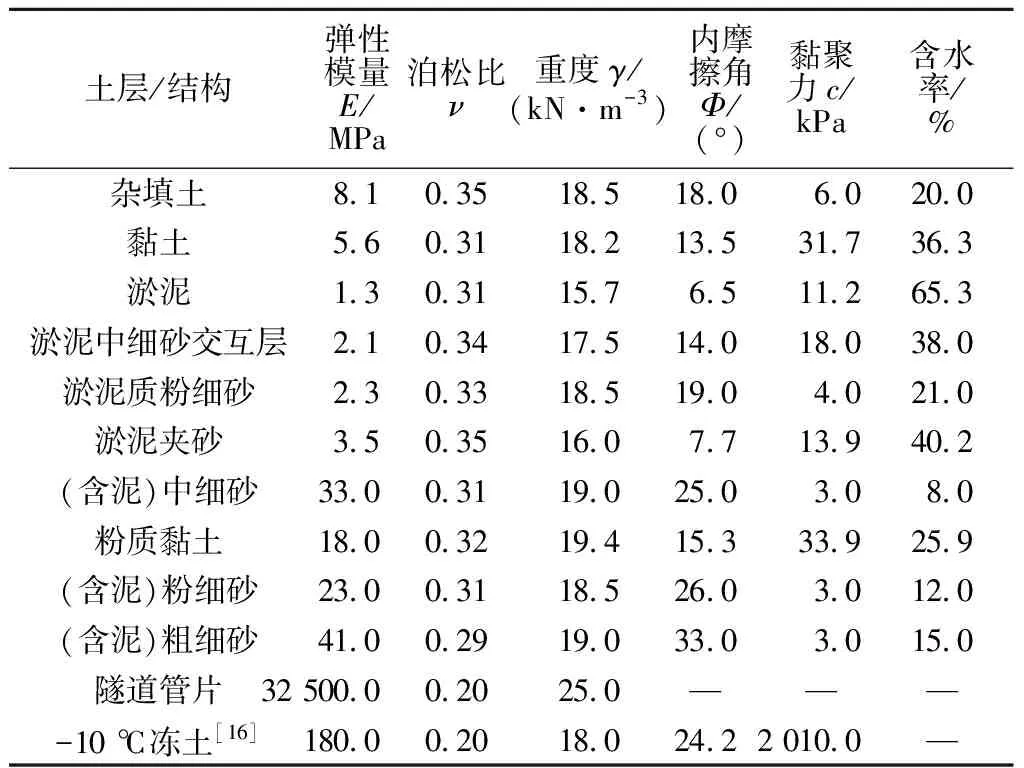
表1 土层和隧道结构物理力学参数Table 1 Physical and medchamical parameters of soil layer and channel structure

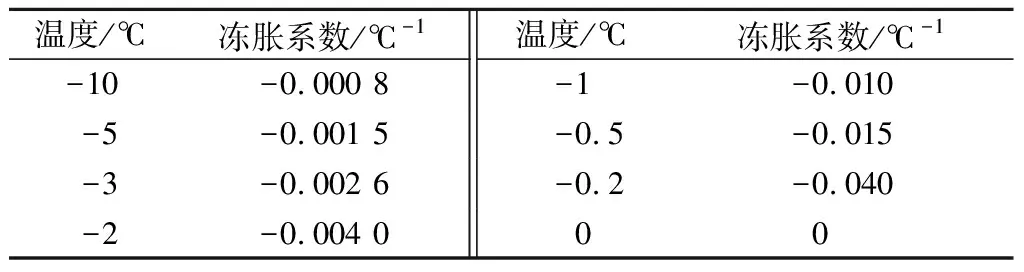
表3 土层冻胀系数Table 3 Coefficient of frost heave of soil strata

借鉴参考文献[18]选取)。按表2所示的温度节点并设定相对应节点的热力学参数，而两温度节点之间的参数则采用线性内插获得。

本次计算模型的单元划分主要为四面体单元及六面体单元，共1 804 457个单元、401 567个节点。单元划分结果见图3。模型除上表面不受自由度约束外，侧面及底面均受法向位移约束。

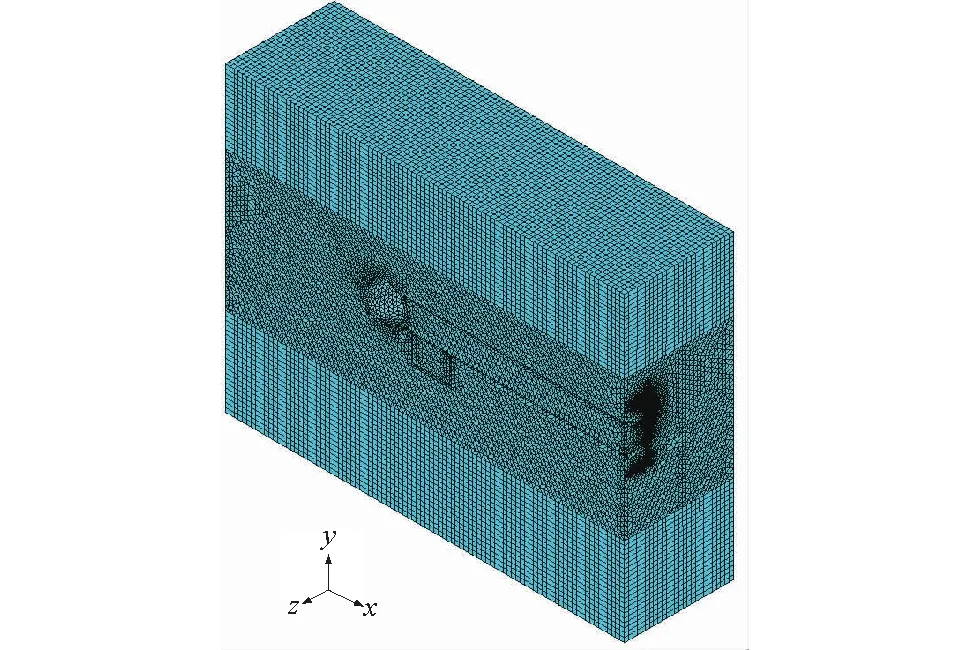
图3 计算模型有限元网格Fig.3 Finite element meshes of computational model

3.2 冻结过程模拟

冻结过程温度场计算采用瞬态热分析，温度单元选用SOLID70，设定土层温度为25 ℃。温度荷载根据预计盐水降温曲线施加于冻结管外壁上。

在获得冻结温度场的结果后，单元转化为SOLID165进行结构分析。首先将地层进行地应力平衡后并位移清零，再将温度场计算结果作为结构分析的温度荷载，导入已转换成结构单元的计算模型中进行结构位移场分析。

4 计算结果分析

4.1 冻结温度场数值分析

为反映截面中温度随冻结时间的变化特性，分别在冻结管交叉及泵站截面位置现场布设温度测点，测点位置如图4所示，其中测点1、3、5为交叉截面测点，测点2、4、6为泵站区域截面测点。再根据现场测点位置情况提取数值分析中相应测点的计算结果与现场实测进行对比，对比情况如图5所示。

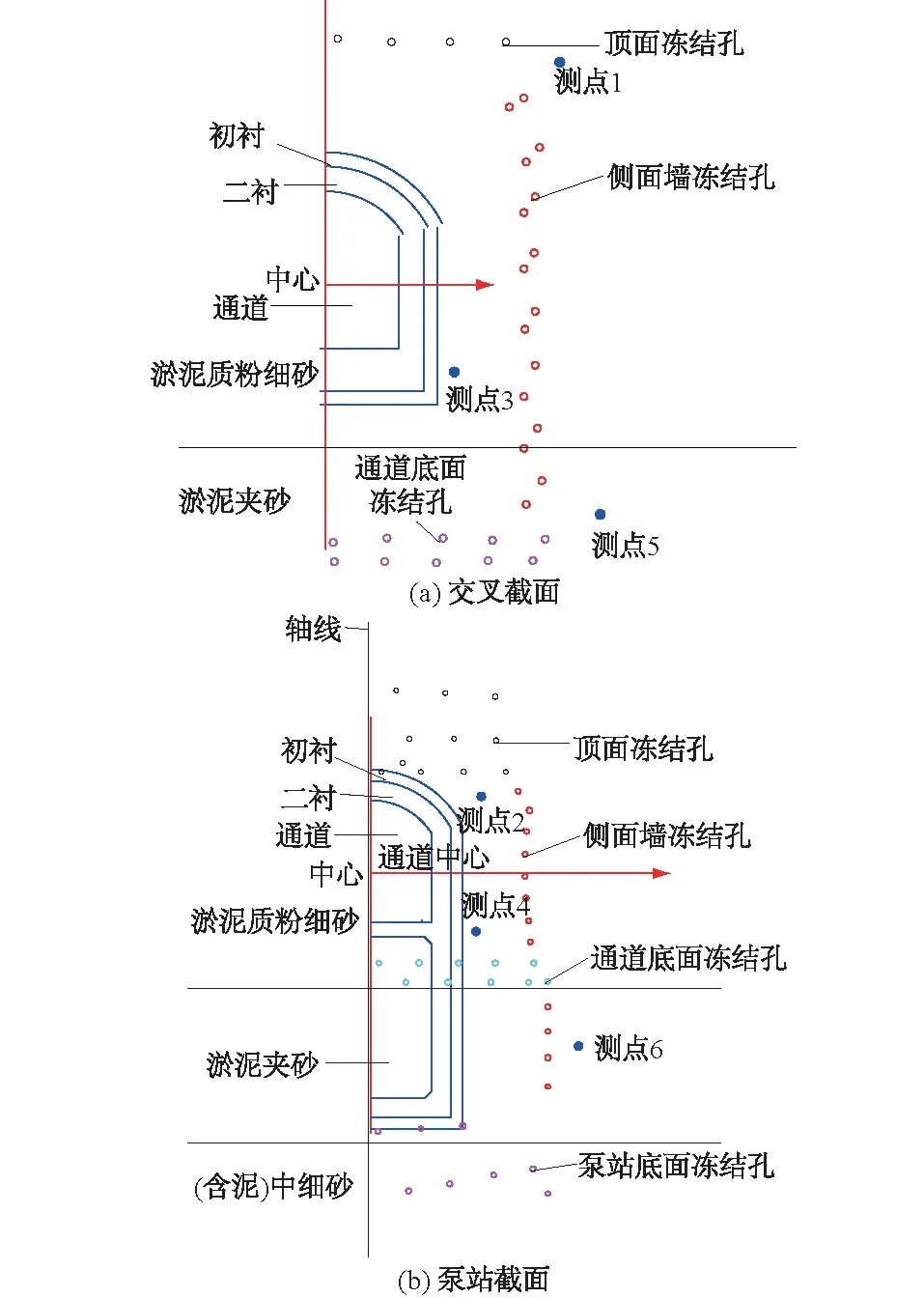
图4 交叉截面、泵站截面温度测点位置Fig.4 Positions of temperature measuring points in cross section and pump station section

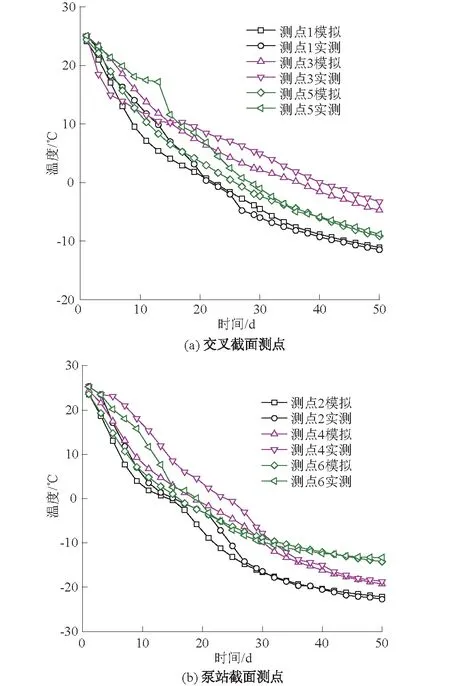
图5 交叉截面测点、泵站截面测点温度变化Fig.5 Variation of temperature at measuring points in cross section and pumping station section

通过图5(a)可以看出，测点1中模拟与实测温度变化趋势一致，20 d后两者逐渐接近并趋向于-12 ℃；测点3模拟与实测温度在前15 d存在较大差异，但之后两者温度变化趋势逐渐相同，到冻结期50 d两者温度皆稳定在-4 ℃；测点5模拟与实测温度变化趋势相同，在积极冻结期间前25 d实测温度略大于模拟温度2～5 ℃，31 d后两者之间温差在1 ℃之内。

通过图5(b)可以看出，测点2中实测温度比模拟温度发生相变的时间多5 d，但在整个积极冻结期内，两者温度曲线基本重合一致；测点4中模拟与实测温度在相变之前相差较大，而后两者之间的温度逐渐趋向于一致；测点6除了在前15 d模拟温度比实测温度略低之外，之后整体温度变化是一致的，偏差皆在1 ℃以内。

综上所述，冻结初期土层温度受外界因素影响波动大,导致个别测点在冻结初期偏差略大，积极冻结中后期各测点模拟与实测温度偏差在1 ℃以内，在可接受范围之内，因此该冻结过程模拟是合理的。同时可知，距离冻结管0.5 m以内的区域，其在冰点附近发生的相变转折点明显；主要是由于该处区域的降温速率快，水相变所释放出潜热的速率也越快，当热量不能及时被带走时，就会出现明显的降温转折点。

通过对比图5(a)、图5(b)发现，泵站截面的温度下降速率普遍大于交叉截面，泵站截面处冻结约13 d时测点温度已开始出现0 ℃，冻结30 d测点温度全部达到-10 ℃以下。交叉截面21 d测点温度才开始达到0 ℃以下，到50 d仍存在部分测点温度在-5 ℃。由此可见，泵站区域截面温度下降速率快，冻结50 d后盾构隧道与冻土帷幕之间的胶结要求完全能够满足。且从整个积极冻结期可知，泵站截面处发生相变现象的转折点比交叉区域截面明显。

4.2 冻结温度场云图结果

通过ANSYS有限元软件对冻结过程中土体温度场进行分析计算后，考虑通道冻结管交叉区域距隧道距离最远，冻结效果差异较大。因此分别提取前后对称截面、中间冻结管交叉区域横截面、泵站所在区域横截面3处的积极冻结期温度场，见图6—图8。

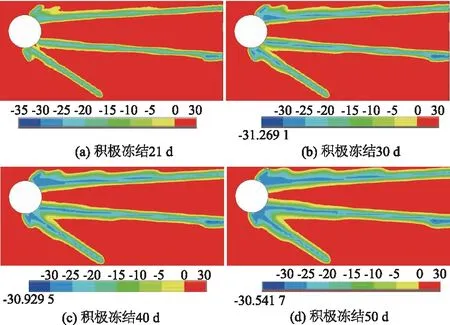
图6 对称截面温度场变化Fig.6 Variation of temperature field on symmetrical section

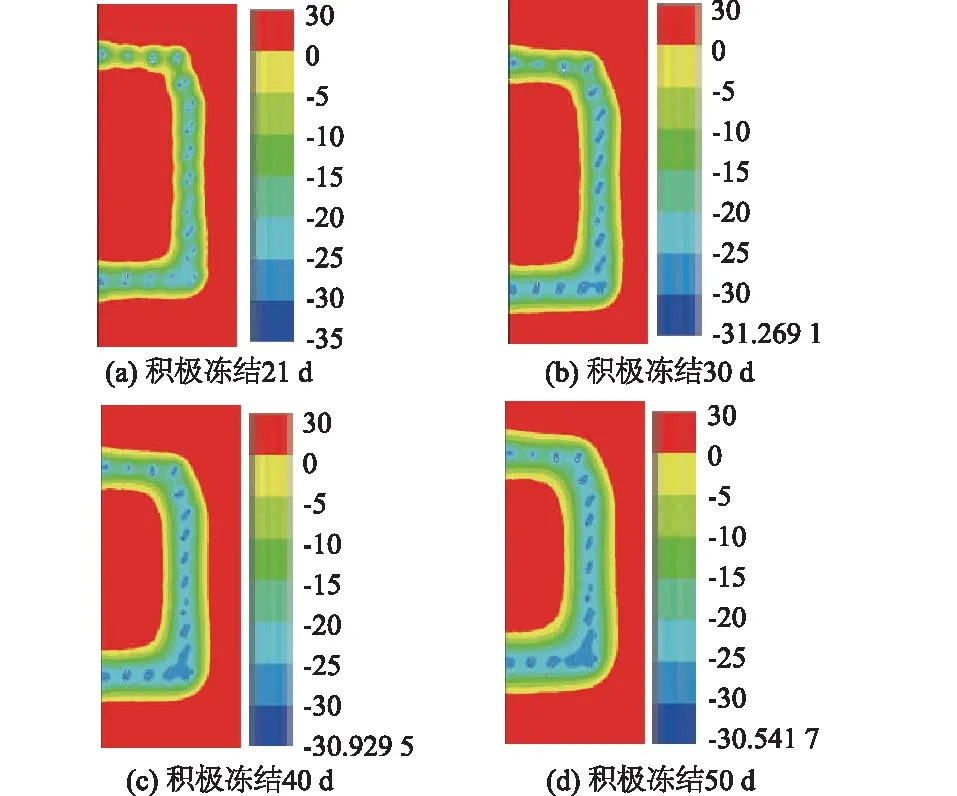
图7 交叉截面温度场变化Fig.7 Variation of temperature field in cross section

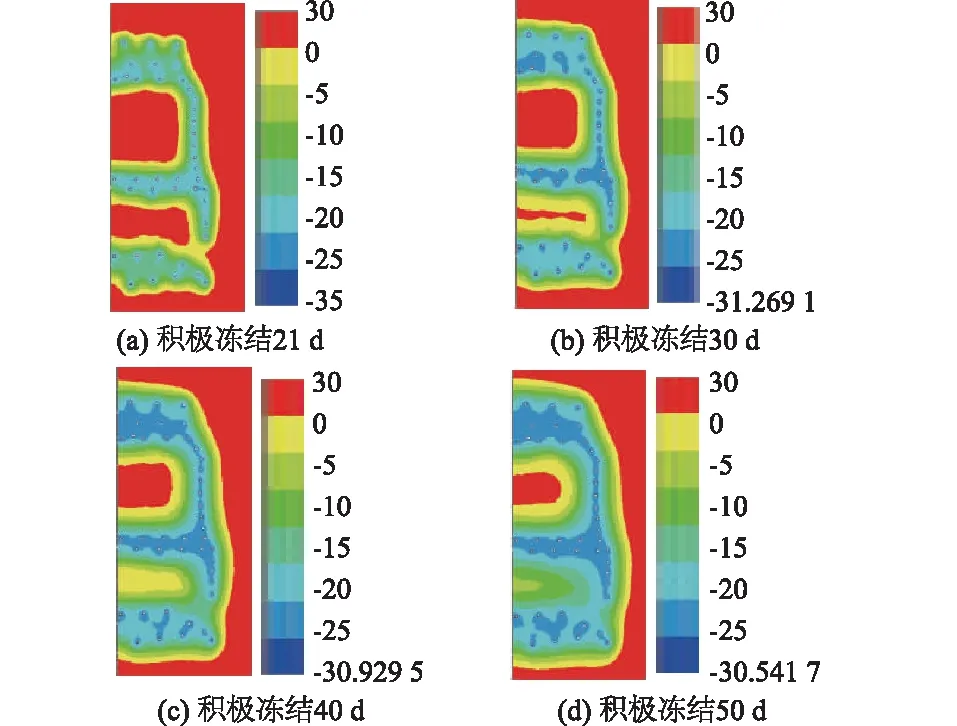
图8 泵站截面温度场变化Fig.8 Variation of temperature field in pumping station section

通过图6可以看出，在无偏斜条件下冻结管交叉区域0 ℃的冻结壁边界在冻结前21 d扩散到1.2 m厚，平均速率57 mm/d，后29 d只增长0.8 m，平均速率27.6 mm/d。这主要是由于冻结初期温差大，土体吸收的冷量多。冻结中后期，土层间温差减小且土体在冰点附近发生相变放热，同时冻结管周围土体温度低，使得冻结管与土层热交换降低，从而导致后期冻结温度发展变慢；联络通道出入口处冻结管密集，该处受冻结影响最深，喇叭口处冻结壁厚度达2.2 m，越靠近通道中心，冻结壁渐薄。通过图6(d)可以看出，在积极冻结50 d后，冻结管交叉区域的冻结壁比通道正常段厚0.5 m。可见冻结管合理的交叉对长联络通道中间段冻结壁形成具有一定增益效用。同时可以观测到喇叭口周边区域温度皆达到-25 ℃的低温环境，说明该处冻土强度与安全系数高。

通过图7可知，交叉截面处在积极冻结21 d后冻结壁已经形成并且厚度达到1.2 m。积极冻结50 d后，冻结壁平均温度降至-10 ℃且厚度达到2.05 m，满足设计要求。由图8可知，积极冻结21 d时下部泵站周边冻结壁交圈刚形成不久，厚度仅为0.9 m，而上部通道周边冻结壁则已初具规模，厚度达1.2 m，导致差异的原因主要为通道周边冻结管布置较泵站周边密集。在积极冻结50 d后，冻结管围成的泵站中心区域温度下降至-5 ℃以下，在实际中可考虑泵站处采用控制冻结等方式，以减少冷量损失，节约成本。通道区域冻结壁厚度最小达到2.3 m，满足设计要求。

为获得通道两横截面处的温度与距中心点水平路径距离关系，以图4(a)、图4(b)轴线上中心点为坐标原点，箭头方向上距中心点的距离为x轴，温度为y轴建立冻结期50 d时泵站及冻结管交叉区域截面处温度随路径距离变化关系，如图9所示。

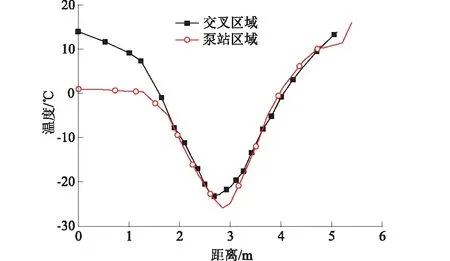
图9 通道温度随路径距离变化关系Fig.9 Variation of temperature at connecting aisle with axial distance

通过图9可以看出，泵站与交叉区域温度随着距离变化规律具有异同点，在冻结孔内侧距离通道截面中心1.2 m(离冻结管1.5 m)处，温度变化速率明显变快，且因泵站区域冻结管密集,温度改变速率比交叉区域明显。在拐点左侧，泵站区域温度比交叉区域低，拐点右侧两者温度变化趋势则基本一致。

4.3 冻结对隧道周边环境影响分析

4.3.1 地层冻结位移场分析

根据数值模拟，提取冻结50 d时通道周边地层位移场，其y方向位移云图见图10，进而可以得到图10中距对称面0、5、10、15 m的地表隆起变形规律，见图11，其中图11(a)为地表隆起变形与左边界距离(左边界为x轴原点)的变化关系，图11(b)为图11(a)中隆起位移对距离的一阶导数。

图10 冻结50 d y方向位移场云图Fig.10 Displacement field in y direction frozen for 50 days

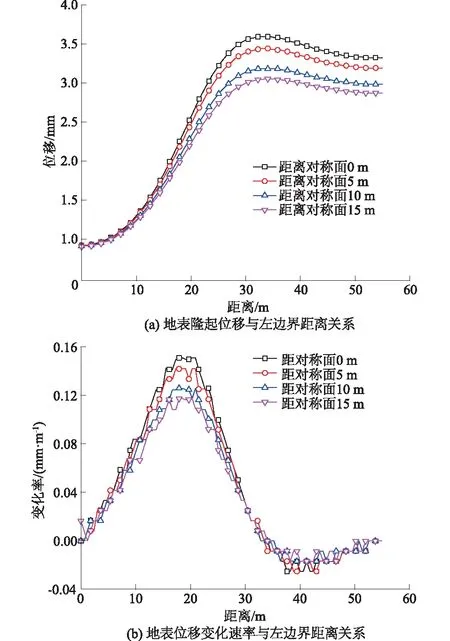
图11 地表不同位置处位移变化规律Fig.11 Law of displacement change at different positions of ground surface

通过图10知，在喇叭口附近出现宽10 m、高2.5 m的变形集中区，其竖向位移介于6～7.2 mm之间，该集中区传至对应地面位移衰减至4 mm；同时，因A-A及B-B处截面冻结管密集，其通道冻胀位移量比两截面之间的普通区多60%～70%。

通过图11(a)知，在距左边界同样距离时，离对称面越远，地表隆起变形越小；随距左边界越远，地表变形越大，在33 m处(距盾构隧道中心8 m)达到最大值3.6 mm，之后又逐渐减小。由图11(b)可知，地表变形速率在16 m处达到最大值0.15 mm/m，在33 m处减小为0 mm/m，在40 m处达到最小值-0.025 mm/m，而后又逐渐增加到0 mm/m，即从33 m至中部的地表起伏平缓。

同时，提取A-A截面在距对称面0、5、10、15 m处地表位移的时间历程曲线，如图12所示。

图12 地表位移时间历程曲线Fig.12 Time-history curves of ground surface displacement

通过图12可以看出，在积极冻结前5 d地表位移基本不变。之后随着冻结时间增加，地表位移及增长速率皆呈现增长。距对称面愈远，地表隆起值及增长速率愈小。

为得到在冻结50 d时不同深度土层的位移变化规律，考虑图10中A-A(喇叭口附近)和B-B(交叉区域)线所在位置变形较大，则从两处的通道顶部向地面分别选取不同的土层深度，得到以通道顶为坐标原点、距通道顶竖直距离为横坐标、土层位移为纵坐标的位移随深度变化关系，见图13。

图13 地层位移与距通道顶距离关系Fig.13 Relation between soil displacement and distance from aisle top

通过图13可知，A-A、B-B两截面的通道顶部位移分别在5 mm和2.5 mm以内，而距通道分别1.5 m和3 m处土层产生冻胀位移则分别增加至7 mm和5.6 mm，到达地面时，分别衰减至3.7 mm和3.3 mm。可见受联络通道下部冻结管的相互影响，冻结产生的变形最大区域不在通道开挖轮廓边上，而集中于冻结孔周围，特别是冻结孔外侧区域。

综上可知,冻结管周边土层受冻结影响最大且冻结管越密产生的变形破坏越大。通道喇叭口附近会形成变形集中区，对地表的隆起变形具有显著影响。

4.3.2 盾构隧道冻结位移场分析

通过ANSYS有限元软件对冻结过程中隧道进行分析计算后，提取1/4模型隧道的位移、应力云图，如图14、图15所示。

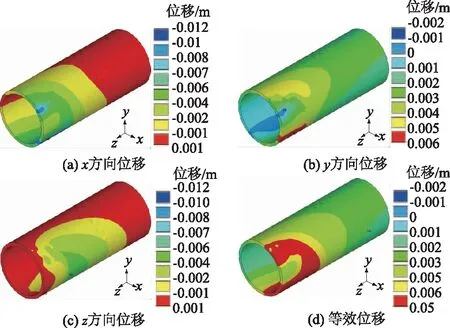
图14 盾构隧道位移云图Fig.14 Displacements of shield tunnel

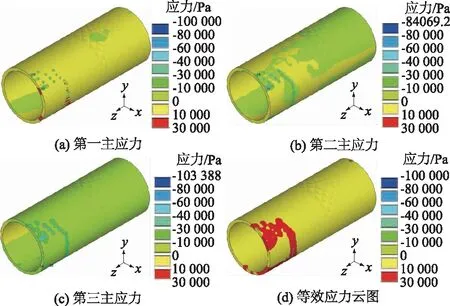
图15 盾构隧道应力云图Fig.15 Stresses of shield tunnel

由图14(a)看出，盾构隧道受冻结影响，通道侧的拱脚及拱肩处x方向位移变形最大，达到-9.4 mm；由图14(b)知盾构隧道在通道侧的拱肩发生0.8 mm沉降位移，而拱脚则产生5.5 mm隆起位移；z方向位移最大位置也发生于隧道拱脚位置，达到-6.9 mm；通过等效位移图看出，盾构隧道位移变形集中于冻结孔所围成的区域，冻结孔越密集产生的变形位移也越大，最大等效位移在拱脚处达10.3 mm。

由图15(d)看出，距冻结孔中心240 mm范围的等效应力最大，达到48 kPa；由图15中的(a)—(c)知，冻结孔周边的主应力皆较大，特别是在拱脚区域的第一主应力达到22 kPa，但仍远小于混凝土的强度设计值，可见冻结过程中对盾构隧道的强度方面影响微小，而主要集中于变形破坏。因此实际工程中对于盾构管片，特别是在拱脚及拱肩侧应加强变形控制，必要时需采取预防加固措施。

由图14(d)等效位移云图可知，隧道变形在对称截面最大。因此，分别提取对称面盾构隧道拱顶竖向位移、两侧收敛位移、拱底隆起位移等数据，获得其随时间的变化规律，如图16所示。

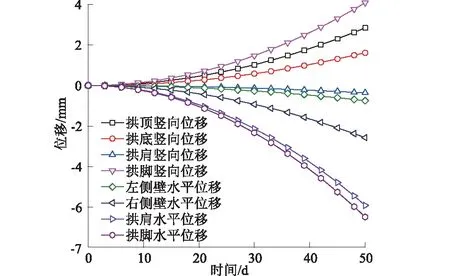
图16 盾构隧道位移随时间历程曲线Fig.16 Time-history curves of shield tunnel’s displacement

由图16可知，盾构隧道在冻结过程中拱顶、拱底及拱脚皆发生向上的隆起变形，且拱脚竖向位移最大，比拱顶多45%。而拱肩则发生微小的沉降变形，说明在拱肩附近存在一竖向变形为0的点。盾构隧道左右两侧壁及拱肩在冻结过程中皆发生远离联络通道侧的水平位移，拱肩发生变形位移最显著，冻结期结束其水平位移比右侧壁多85%；同时可知，随着冻结时间的增加，各点的位移变化速率皆增加，且随着冻结时间的增长，拱脚与拱顶的竖向位移差值逐渐变大。两侧壁的净收敛位移及拱肩与侧壁的水平位移差值增大。这说明联络通道的积极冻结期过长，易造成既有结构物和周边地层过大变形，且时间越长，变形增长速率越快。因此，联络通道应合理采用控制冻结等方式来降低冻胀影响，除能节约工程造价外，还有利于保证既有结构物及地表建筑物的安全。

综上可知，超长联络通道冻结过程对盾构隧道的变形造成很大影响。变形主要集中于盾构隧道近通道侧的拱脚及拱肩部位，其次为拱顶及右侧壁。在实际工程中应加强监控，合理选择冻结工期，必要时需采取相应的预防措施。

5 结论及展望

本文以福州地铁2号线紫阳—五里亭站区间联络通道施工为背景，采用数值仿真对该工程的冻结过程进行模拟分析，并结合现场实测结果得到冻结过程中联络通道及周边区域温度和位移变化规律。主要结论如下：

(1)对交叉区域、前后对称面及泵站截面3处的温度场发展规律进行分析得出，在积极冻结期前21 d，冻结管交叉区域的冻结壁扩散平均速率快，达到57 mm/d，后29 d平均速率只有27.6 mm/d。靠近盾构隧道侧的泵站区域温度场发展慢，其冻结壁交圈时间比通道区域慢8 d；冻结管交叉越密集对冻结壁形成具有促进作用，冻结管密集区形成的冻结壁比邻近普通区厚0.5 m以上。

(2)冻结管中心0.5 m范围内的土体降温速率快、相变放热明显，0 ℃相变转折点持续时间越长相变放热越明显。

(3)积极冻结期喇叭口附近区域存在宽10 m、高2.5 m的变形集中区，对地面产生变形影响最大。

(4)冻结对盾构隧道拱肩水平位移和拱脚竖向变形具有显著的影响，积极冻结期结束拱肩的水平位移比盾构隧道右侧墙多85%，拱脚竖向位移比拱顶多45%，且冻结时间愈长，结构变形及变形增长速率越大。

以上主要是基于滨海地区含水率及导热系数均较大的软弱土层中长联络通道的冻结研究，对于其他土层则具有局限性。并且，长联络通道在施工中所产生的冻结管偏斜及沿程冷量损失程度等问题都比常规联络通道中更加突出，本文尚未涉及此方面的研究。为了能更好地确保地下工程施工的安全性，未来需对这些问题开展深入研究。