从一道圆锥曲线焦点分弦题谈二级结论的巧用
甘肃 何少杰
二级结论源于教材中的基础知识,它是利用基本概念、基本定理,经过归纳、推理、证明,总结出来的结论;它是特定条件下一些解题步骤的有序整合.
圆锥曲线是高中阶段解析几何的重要内容,坐标法建立了方程与曲线之间的联系,为“数形结合”架起了桥梁.虽然在教学中我们一直强调通性通法,但在解答选择题或者填空题时,如果利用通性通法联立方程,就可能会陷入繁杂的运算,如果能够灵活地利用好二级结论,就可以规避掉大量重复的计算,节省时间,提高解题效率,巧妙地解决问题.在高考中,焦点弦问题是圆锥曲线考查中的热点,圆锥曲线中的二级结论很多,下面以一道示范性较强的焦点分弦问题为例,通过多种解法对比,来说明利用圆锥曲线中常用的二级结论解决问题的高效性,体会由一题多解到多解归一的过程.
一、试题呈现
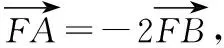
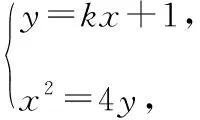
评析:代数方法求解此题时,为避免反复计算,使用韦达定理与向量知识整合是一种不错的方法,而且也是通性通法,但这样的解答并无亮点,有些同类题目可能运算量会比较大,浪费时间.
解法2:

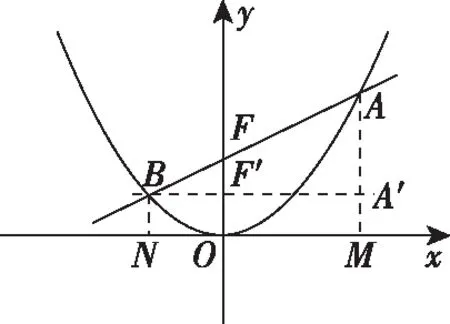
评析:本题虽然使用了数形结合的方法,但未找到解题的捷径,显然比较烦琐.
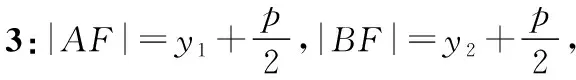
评析:这一解法使用了两个公式:焦半径公式、弦长公式,解法很有技巧,渗透了函数与方程思想,与圆锥曲线中常用的设而不求方法,看似巧妙,但事实上仍是通性通法的灵活运用,虽然回归了定义,但仍显烦琐,除了函数方程思想外,解析几何还讲究“数形结合”,巧妙使用平面几何知识往往能加快解题速度.
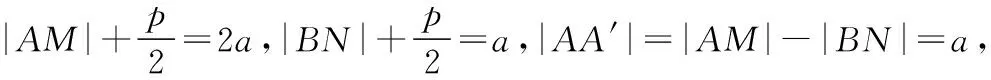
评析:借助圆锥曲线的第二定义,同时使用了数形结合的方法,直观易懂,在解决选择、填空一类题型时较好.


得cos2α·t2-4sinα·t-4=0,
设|AF|=|t1|,|BF|=|t2|,可知t1>0,t2<0,t1=-2t2.
评析:以上解法除解法1外,其余方法技巧性较强,不是通性通法,适用范围受到限制,而解法1为通性通法,以代数方法为主,运算较为烦琐,解法4是最为巧妙的方法,那么能否借助解法4找到一种普遍使用的公式解决圆锥曲线中焦点分弦一类问题呢?
二、利用二级结论,高效解题
以此题为背景,对圆锥曲线进行进一步的探索,利用已有的二级结论,获得求解焦点分弦一类题型的一般性方法,从而有效避免繁杂的计算.
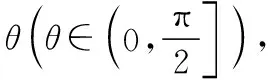
1.对于横向型圆锥曲线
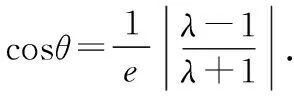
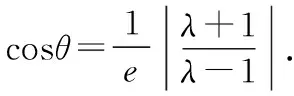
2.对于纵向型圆锥曲线

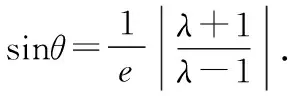
下面对这一二级结论进行证明.
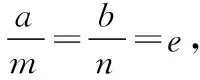
1.对于横向型圆锥曲线
(1)当焦点F内分弦AB时,以椭圆为例进行证明:

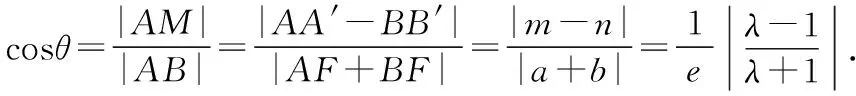
(2)当焦点F外分弦AB时,此时曲线为双曲线.

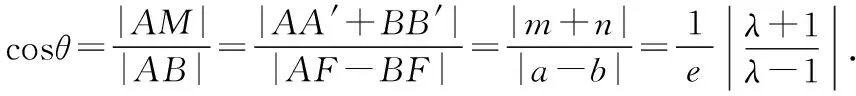
2.对于纵向型圆锥曲线

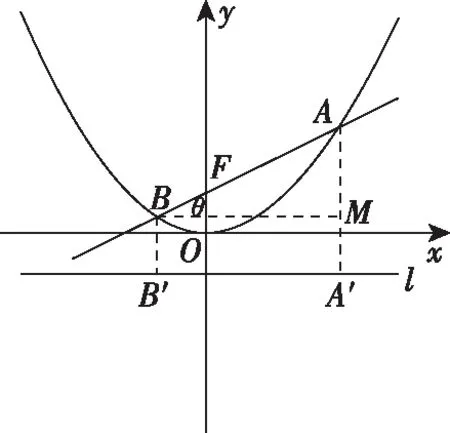
(2)当焦点F外分弦AB时,曲线为双曲线.
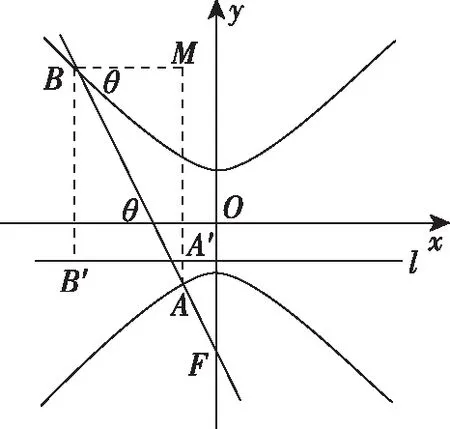
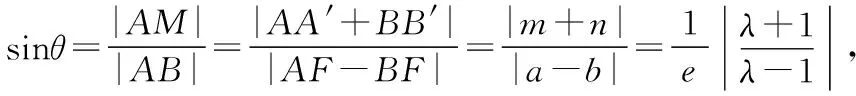

根据圆锥曲线的极坐标方程易得以下结论:
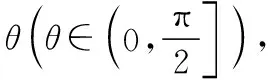
1.对于横向型圆锥曲线
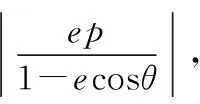
2.对于纵向型圆锥曲线
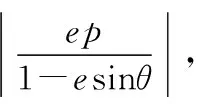
这一结论的证明这里不再赘述.结论1,2揭示了圆锥曲线焦点分弦的一些性质及特征,对于求解圆锥曲线中焦点分弦一类问题大有裨益,不妨运用结论1,2,继续求解此题.
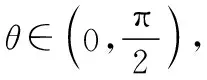
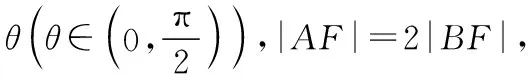
评析:与前面五种解法相比,结论1,2的使用大大的减少了此类题目的运算量,可以起到化繁为简的作用,达到事半功倍的效果,而且也是求解此类题目的统一简解,是通性通法的使用.


