基于SRUKF的模型辅助AUV惯性导航系统
王科宇,王俊雄
(上海交通大学 船舶海洋工程国家重点实验室,上海 200240)
0 引 言
水下自主航行器(AUV)可用于海底资源勘探、目标侦察等,是开发海洋的重要工具。小型AUV 具有成本低、作业方便等优点,随着海洋开发与商业化的深入,逐渐成为AUV 的重要发展方向[1]。小型AUV 执行任务多样,作业水况复杂,对于自主定位导航能力要求较高。低功耗、高可靠的导航定位方案成为小型AUV 开发亟待解决的研究热点。
大量的AUV 导航系统,依赖多普勒测速仪、深度计、磁力计等传感器测得数据进行导航,而小型AUV 限于成本、功耗与体积,往往不能装备足够多的传感器。同时由于小型AUV 作业工况复杂,多普勒测速仪等在某些情况下不能正常工作,导航系统的可靠性低。基于微机电系统(MEMS)的惯性导航系统(INS),成本低、体积小、不依赖外界信号、反应迅速,是AUV 重要的导航方案。本文基于平方根无迹卡尔曼滤波算法,设计了非线性滤波器,并使用模型辅助提高算法精度。同时经过半实物与仿真实验,验证了算法的有效性。
1 AUV 建模
1.1 坐标系定义
在导航中使用2 种坐标系。一种是惯性坐标系On-XnYnZn,固结在地球上。另一种是载体坐标系Ob-XbYbZb,固结在AUV 重心上。为直观起见,采用欧拉角表示载体坐标系相对惯性坐标系的旋转。定义载体坐标系相对惯性系按X-Y-Z轴依次旋转,其欧拉角为[φ,θ,ψ]T,则 φ,θ,ψ分别为AUV 的横滚角、纵倾角、首向角,如图1 所示。
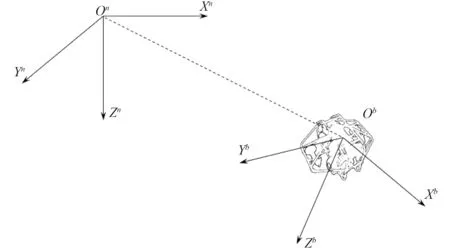
图1 坐标系定义Fig.1 The definition of coordinate
1.2 运动学与动力学建模
设AUV 在惯性坐标系下的坐标为η1=[x,y,z]T,令η2=[φ,θ,ψ]T,AUV在载体坐标系下的速度为ν1= [u,v,w]T,角速度为ν2=[p,q,r]T,令η=[η1,η2]T,ν=[ν1,ν2]T,则可建立AUV 的运动学模型如下:
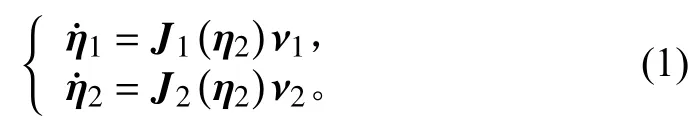
其中:J1,J2为转换矩阵,将正弦函数记作s,余弦函数记作c,正切函数记作t,则

水动力外形对于AUV 的影响十分显著,本文基于Kambara ROV 水动力外形参数建立AUV 六自由度动力学模型[2]为:
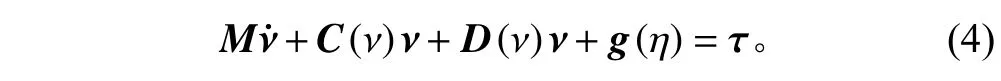
其中:M=MA+MRB为质量矩阵,C=CA+CRB为科氏矩阵,D为水动力阻尼矩阵,g(∗)为回复力,τ为AUV 所受合外力,则


2 惯性导航算法设计
传统的模型辅助AUV 导航定位[3],在AUV 速度计算中引入模型辅助作为参考,忽略了AUV 模型在姿态解算中的潜在应用[4]。为了综合利用AUV 传感器测得信息和模型解算得到的加速度与角速度信息,本文设计了基于平方根无迹卡尔曼滤波的惯性导航算法。本文采用的惯性导航系统结构框图如图2 所示。

图2 惯性导航系统结构框图Fig.2 The diagram of inertial navigation system
2.1 位姿解算算法设计
在惯性导航算法中,为降低运算量,并避免奇异角等问题,使用单位四元数q实时解算AUV 姿态。载体坐标系与惯性坐标系重合时,四元数q=[1,0,0,0]T。
苏州吉恒纳米科技有限公司是上市控股公司控股,主要从事表面PVD涂层,公司拥有一批十几年涂层经验的专业团队,引进欧洲先进的PVD涂层设备,致力于成为国内高端涂层加工服务厂商,丰富的生产经验,完善的质量管控,严谨工艺开发,齐全的检测设备。在确保质量稳定的前提下,提供了客户最快的涂层交期与完善及时的售后服务。保证了在同行业中拥有强大的竞争力。
设k时刻AUV 角度变化量为Δθ=[θx,θy,θz]T,加速度值为ak=[ax,ay,az]T。采用角度变化量形式的毕卡算法求解四元数[5]。本文采用4 阶近似形式以保证精度,则
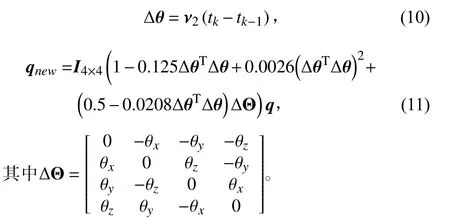
为直观表示滤波效果,将四元数姿态表示转换成欧拉角表示。四元数q 与欧拉角[φ,θ,ψ]T有以下转换关系:
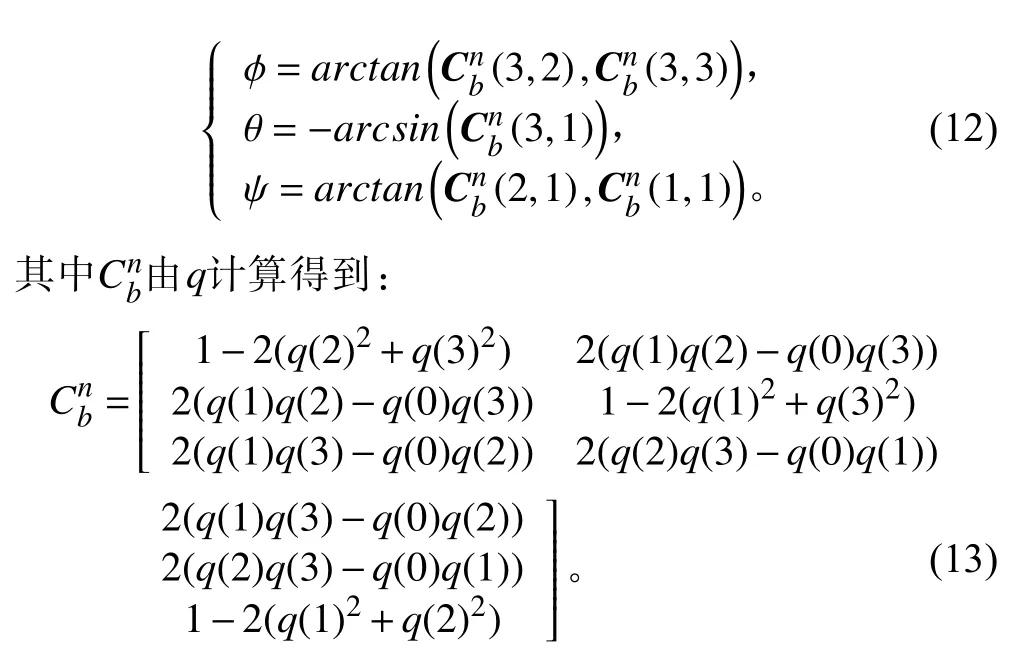
小型AUV 由于体积、功率限制,其加速度变化率有限,因此采用tk时刻与tk−1时刻的加速度平均值作为tk−tk−1时间段的加速度值近似平均值,并计算得到tk时刻速度值。同理,采用惯性坐标系下tk时刻与tk−1时刻的速度平均值作为tk−tk−1时间段的速度值,并与AUV 运动学方程联立,计算得到tk时刻AUV 坐标。
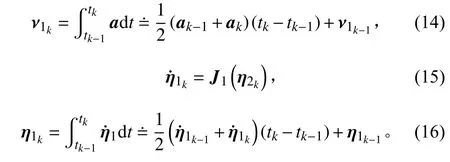
2.2 平方根无迹卡尔曼滤波算法设计
由式(4)可知,AUV 的6 个自由度间的运动互相交叉耦合,运动方程高度非线性化。扩展卡尔曼滤波(EKF)在计算时使用一阶泰勒展开线性化状态方程,性能不稳定,结果易发散。本文采用平方根无迹卡尔曼滤波算法对传感器数据与AUV 模型计算得到数据进行滤波融合处理,通过选取sigma 点进行无迹变换,匹配AUV 运动数据的统计特性,从而保障了估计精度[6–7]。同时,在滤波中使用协方差平方根代替协方差进行运算,保障了协方差的对称正定性,避免滤波算法因舍入误差积累而发散,提高了算法稳定性。
选取AUV 运行时的加速度a与角速度ν2作为系统状态量,则X=[a,ν2]T。选取MEMS 惯性测量单元(IMU)测量得到的加速度与角速度作为系统观测量,则
设计平方根无迹卡尔曼滤波算法:
1)参数设置及初始化
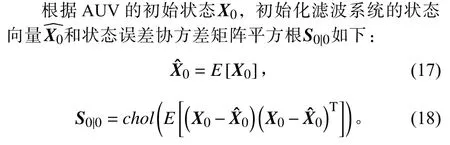
其中chol(A)为矩阵A的Cholesky 分解的上三角矩阵。
2)计算sigma 点
采用对称选点的方式,选取sigma 点近似非线性系统的统计特性。根据噪声的分布特性确定sigma 的点数。
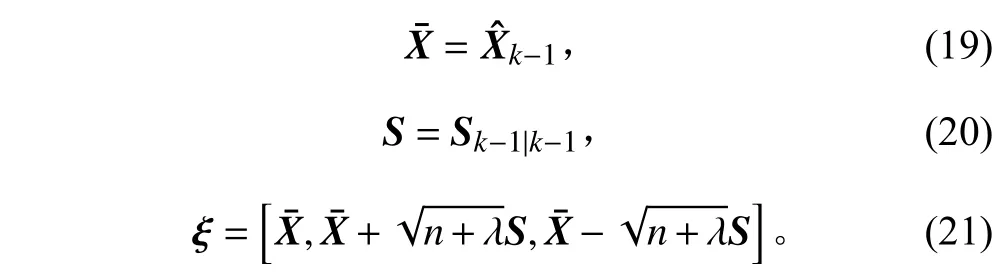
其中n为 系统状态量的维度,此处n=6。λ=α2(n+κ)−n,α,κ为第一、第三刻度因数,决定sigma 点距离平均值点的离散程度。
3)计算时间更新方程
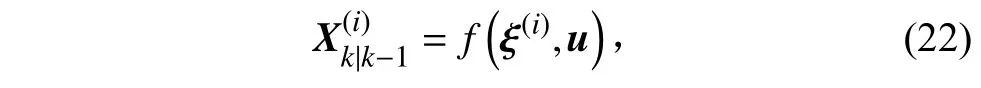
式中:f(*)为滤波系统的状态方程,这里为AUV 动力学方程式(4),u为上一步滤波后INS 系统解算得到的AUV 姿态、速度数据以及AUV 受到的推进力。
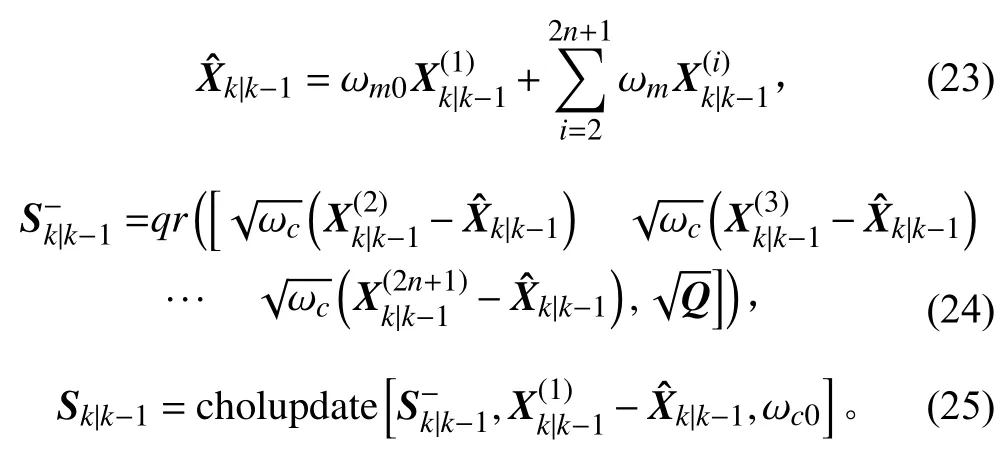
其中:qr(A)计算矩阵A的QR分解的上三角矩阵;cholupdate(R,x)计算矩阵A+x∗x−1的Cholesky 分解的上三角矩阵,其中R=chol(A);ωm,ωc,ωm0,ωc0按照以下公式计算得到:

5)结果更新
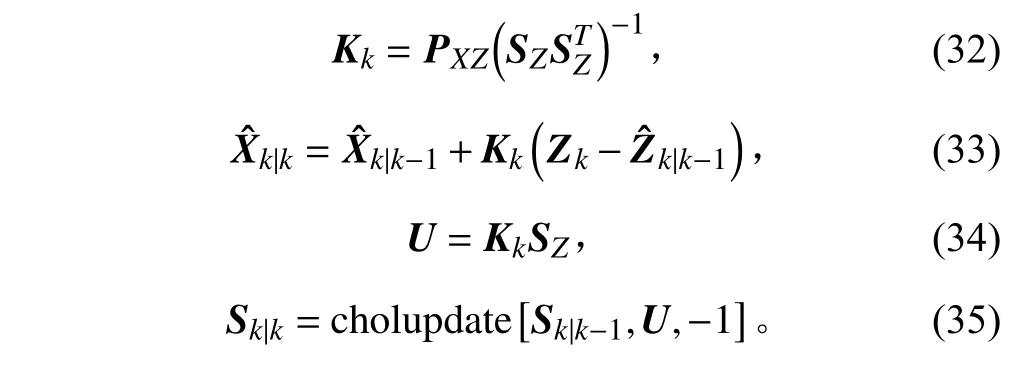
3 仿真、实验与结果分析
使用手机模拟AUV 进行算法的静态测试。将手机静置,基于手机内置MEMS IMU 得到加速度与角速度测量数据,并输入导航算法中进行测试。滤波、解算得到AUV 静态时姿态如图3 所示。由图可知,基于SRUKF 的惯性导航算法能够较好补偿静态误差,角度误差在0.3°以内,且误差增长缓慢。

图3 静态姿态解算结果Fig.3 The angle estimation with still state
使用Matlab 搭建仿真模型,测试AUV 动态运行时惯性导航算法的性能。仿真程序的仿真流程图如图4所示。
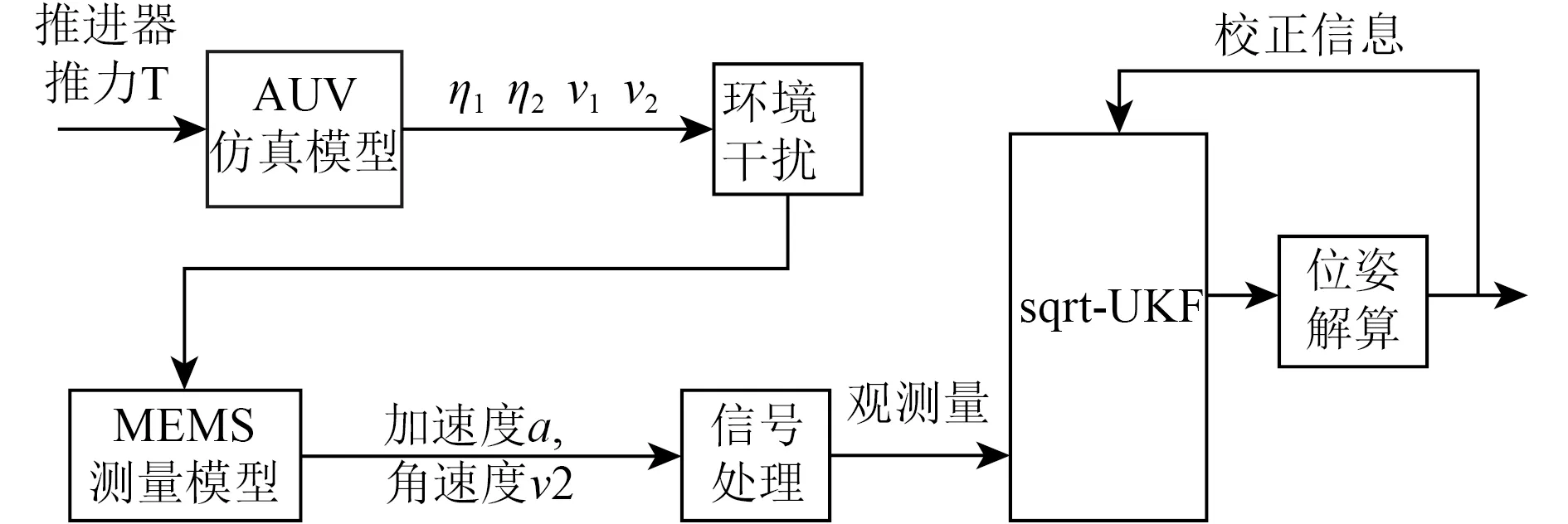
图4 仿真流程图Fig.4 The diagram of simulation flowchart
考虑MEMS 传感器的刻度因子误差、非正交安装误差、系统误差等,建立加速度传感器的误差模型:


其中βt是t时刻角速度计的白噪声。
基于上述仿真模型,进行动态误差测试。计算AUV 在纯惯性导航(INS)、使用EKF 滤波(INS+EKF)、使用SRUKF 滤波(INS+SRUKF)3 种情况下的导航效果。解算得到AUV 姿态、速度、位置数据和误差如图5~图10 所示。
由图5 和图6 可知,INS 解算的姿态和速度误差积累迅速。由图7 可知,INS 解算位置误差迅速达到百米量级,x轴误差已大于1 000 m,使得解算结果完全不可用。
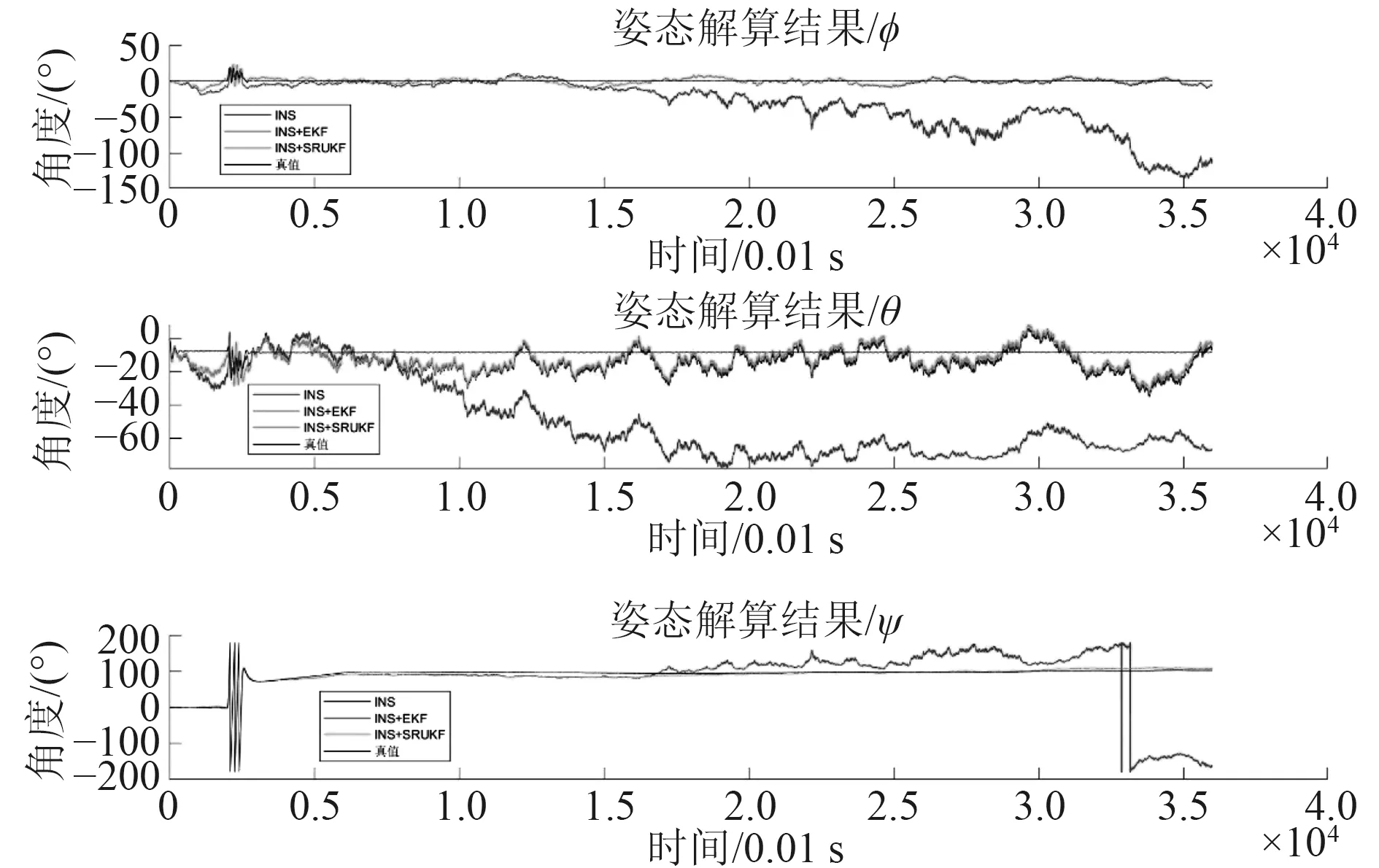
图5 姿态解算结果Fig.5 Angle estimation
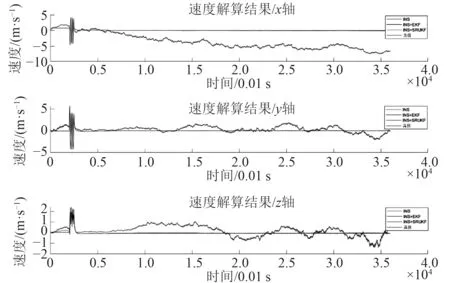
图6 速度解算结果Fig.6 Velocity estimation
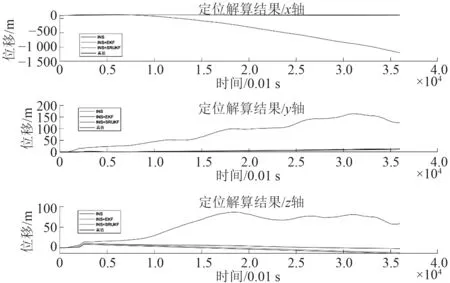
图7 位置解算结果Fig.7 Position estimation
由图8 和图9 可知,INS+EKF 解算出的姿态和速度误差均大于INS+SRUKF 解算结果,且由图10 可知,由于位置由速度和姿态积分得到,速度和姿态的误差经积分运算迅速扩大,使得INS+EKF 导航的结果更加不可靠。分析可知,AUV 受力简单、工作平稳时工作点的1 阶泰勒展开能较好反应AUV 运动状态,此时INS+EKF 解算效果较好。当AUV 突然改变工况、六自由度运动相互影响加剧时,INS+EKF 出现发散现象。
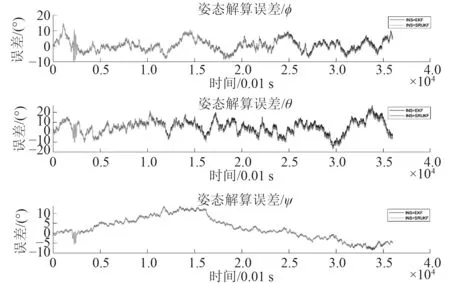
图8 姿态解算误差Fig.8 The error of angle estimation
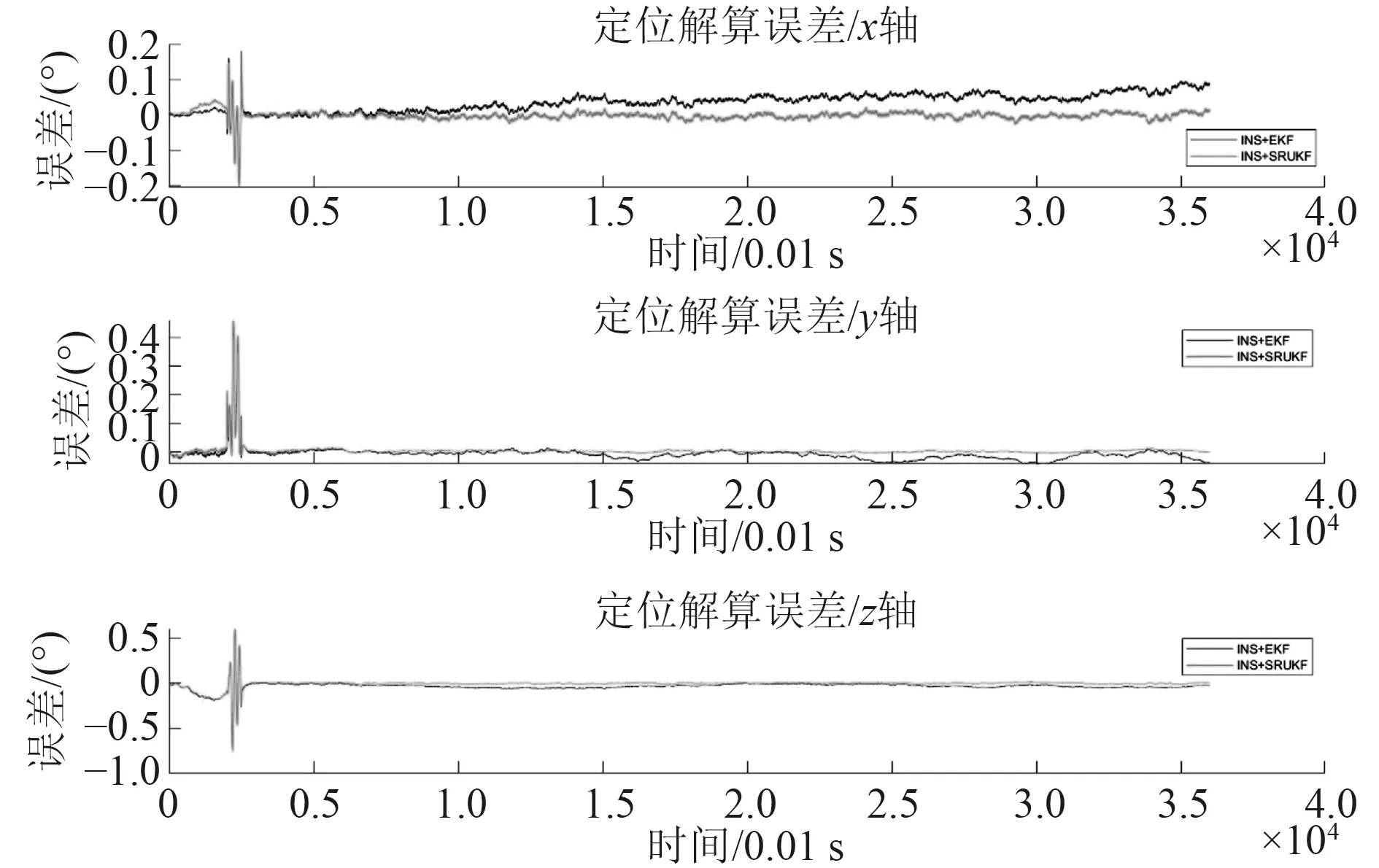
图9 速度解算误差Fig.9 The error of velocity estimation
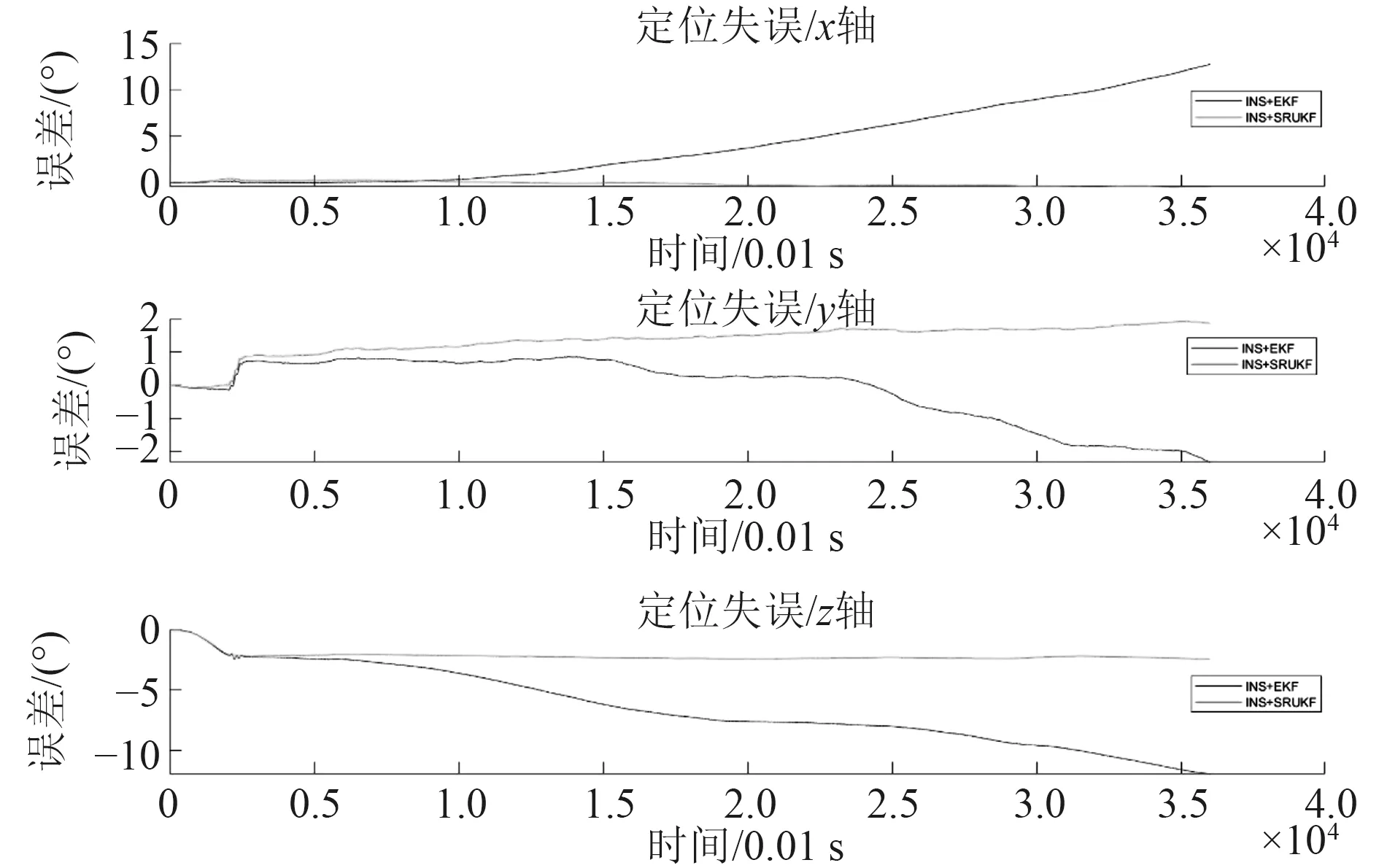
图10 位移解算误差Fig.10 The error of position estimation
使用INS+SRUKF 进行解算,AUV 工作平稳时解算结果与INS+EKF 基本一致,当AUV 突然改变工况时,仍能较好解算AUV 位置。速度、姿态误差的增加主要出现在AUV 工作状态突然改变时。定位误差随时间增长,但增长缓慢。其最大定位误差小于2 m。
4 结 语
通过建立小型AUV 的运动学和动力学模型,解算得到AUV 的运动状态和位置信息,可以为限于功耗、体积而不能装备足够传感器的小型AUV 提供定位导航参考。设计平方根无迹卡尔曼滤波算法,综合利用AUV模型解算数据和MEMS IMU 测量数据,并能够克服AUV 运动方程高度非线性的困难,提高惯性导航精度。同时经过半实物实验和Matlab 仿真实验,验证了算法的可行性。结果表明,基于模型辅助的平方根无迹卡尔曼滤波算法,性能优于扩展卡尔曼滤波算法,能够显著提高惯性导航的精度,满足小型AUV 的导航定位需求。

